基于数字图像直方图均衡化改进算法的设计研究①
2018-12-27
(马鞍山师范高等专科学校,安徽 马鞍山 243000)
0 引 言
为了保持图像的亮度特征,许多学者开始研究局部增强处理技术,并相继提出了许多新的算法,比如递归均值分层均衡处理算法(RMSHE)、递归子图均衡算法(RSIHE)、动态直方图均衡算法(DHE)、多层直方图均衡算法(MHE)等等[1]。国内一些学者针对直方图均衡化处理过程中可能存在的图像灰度级被过多合并的现象,提出了保留灰度级的直方图均衡化方法,一定程度上消除了灰阶合并所带来的图像的不连续性[2]。然而,经典的直方图均衡化算法在增强图像的过程中存在一定的局限性,但需要研究其改进算法。鉴于此,对两种直方图均衡化改进算法进行研究,编写MATLAB代码实现并进行仿真,以及利用仿真结果进行比较。
1 基于抛物线调整的直方图均衡化算法改进及MATLAB仿真设计
1.1 算法简介
基于抛物线的直方图均衡化算法采用抛物线形式的映射函数[3],映射函数为
y=axn
其中,a表示增强后图像的最大灰度级,x表示变换函数,n代表调节参数。a是用来调节图像的明暗程度的,且a越大,整幅图像越亮;反之整幅图像也就越暗,一般情况下a的默认取值为255。由式y=axn,可知变换函数x的取值范围为[0,1],从而xn的取值范围也为[0,1]。调节参数n可以调节变换曲线,
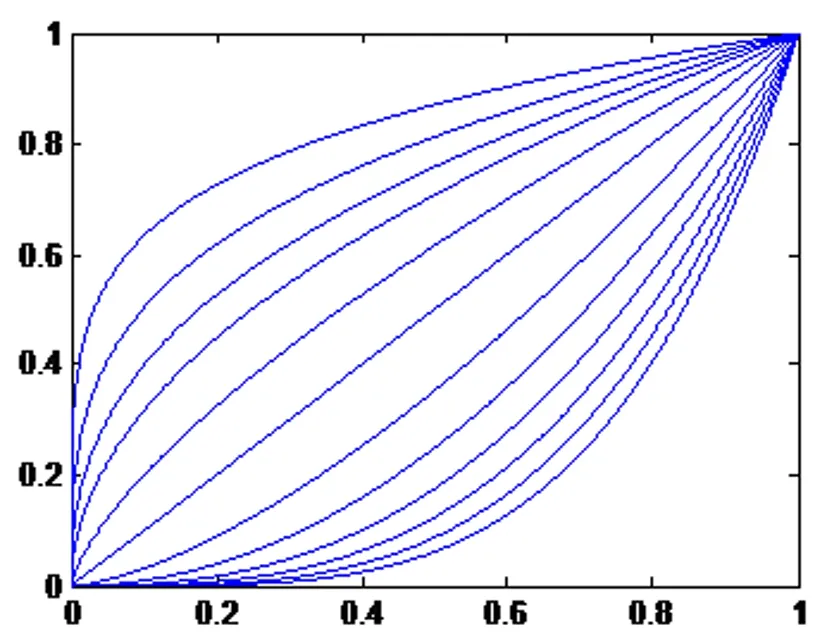
图1 y=xn的抛物线
如图1所示,按从上到下方向,设置n分别取值为0.2、0.3、0.4、0.5、0.7、1、1.5、2、2.5、3、3.5、4。即n与像素的灰度值的改变有关。[5]由此可知,基于抛物线调整的直方图均衡化算法可以通过设置合适的参数来进行调整,从而可以调节图像的明暗程度,或者增强某一灰度范围内图像的对比度[4]。
由图1得:
(1) 当n=1,a=255时,则与经典直方图均衡化算法保持一致;
(2) 当n>l时,且n值越大,那么高值灰度区间灰度级的拉伸程度也就越大;
(3) 当n<1时,且n值越小,则低值灰度区间拉伸程度也越大。
由上述分析,直接使用参数来进行调节,可以实现某一灰度范围的扩张或压缩,增强局部区域的对比度,应用比较灵活方便,但是参数值的选取则需要根据不同的情况来确定。
1.2 算法步骤

1.3 实验结果与分析
下面使用MATLAB对图像进行增强处理。
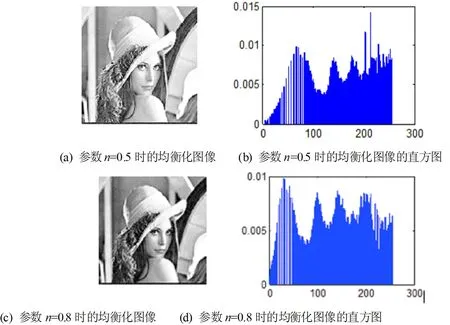
图2 n<1时基于抛物线调整的直方图均衡化改进算法
由图2中的图(a) 和图(b)可知,原始灰度图像的直方图中低值灰度级所占比例较大,整幅图像偏暗。图2(a)和(b)分别是参数n=0.5时的均衡化图像及其直方图,图(c)和(d)分别是参数n=0.8时的均衡化图像及其直方图,可以看到,当n<1时,经过基于抛物线调整的直方图均衡化改进算法处理后,整幅图像较原始图像偏亮,部分细节处如少女所佩戴的帽子看上去比较模糊。同时可以发现,当n值越小,图像的高值灰度级部分即原始图像中较亮的区域丢失的信息也就越多;图3(a)和(b)分别是参数n=1.5时的均衡化图像及其直方图,可以看到,当n=1.5时,其灰度分布的动态范围比原始图像的更宽,使得图像的对比度更强,且整幅图像与原始图像的亮度相近,图片左上角看起来也更加清晰;图3的(c)和(d)分别是参数n=3时的均衡化图像及其直方图,可以看到,经过处理后,整幅图像偏暗,导致部分区域处尤其是原来图片中比较暗的地方更暗,甚至看不清楚。可以发现,n值越大,高值灰度区的拉伸程度也就越大,该部分目标则清晰可见,但是同时也会使得低值灰度区的细节不够清晰,导致信息丢失。由以上分析可知,n<1适合增强图像中较暗的区域,而n>1则对于增强图像中较亮区域的效果更加明显。实验结果表明,对于基于抛物线调整的直方图均衡化改进方法,可以根据实际情况来设置适当的参数值,以调整图像的明暗程度,增强图像的对比度,达到增强图像的目的。所以,基于抛物线调整的直方图均衡化改进算法的关键就在于如何选取合适的参数值以提高图像的增强效果[6]。
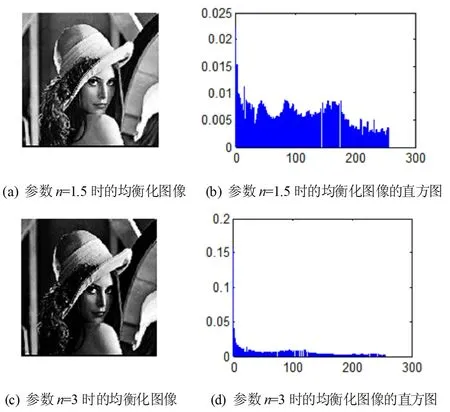
图3 n>1时基于抛物线调整的直方图均衡化改进算法

图4 标准直方图均衡化算法与基于比例的直方图均衡化算法的比较
2 基于比例的直方图均衡化算法改进及MATLAB仿真设计
2.1 算法简介
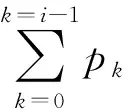
(2)

(3)
其中,qk为第灰度级的像素数,Q为整幅图像的总像素数[7]。
2.2 算法步骤
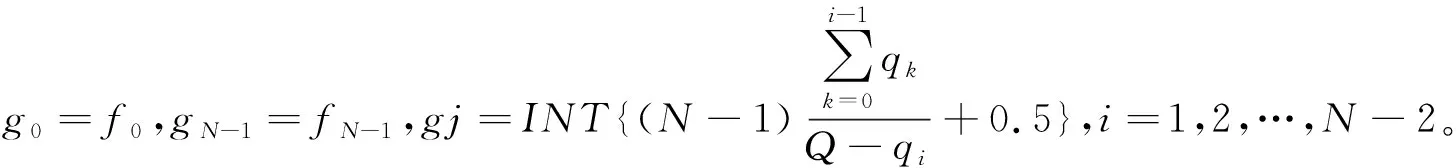
2.3 实验结果与分析
下面使用MATLAB对图像进行增强处理,如下图所示:
由图2中的图(a)和图(b)可以看出,原始图像直方图的灰度分布范围相对较窄,整幅图像偏暗且比较模糊。图4(a)和(b)分别是标准直方图均衡化处理后的图像及其直方图,图(c)和(d)分别是经过基于比例的直方图均衡化处理后的图像及其直方图,不难看出,图(c)比图(a)效果更好。比较图(b)和图(d),可以看到,图(d)直方图中的实际灰度级数比标准直方图均衡化算法处理后图像的灰度级更多一些,相对减少了图像灰度级的合并,且实际灰度分布范围达到了灰度的最大范围,有效地改善了输出图像的视觉效果,图像的增强效果更好。
3 结 论
直方图均衡化及其改进算法进行了MATLAB仿真及图形用户界面设计,并对仿真结果进行分析与比较。根据实验结果可以看出,基于抛物线的直方图均衡化改进算法和基于比率的直方图均衡化改进算法能够更加有效地改善灰度图像的对比度和灰度动态范围。
