四基站时差和牛顿迭代法的三维定位算法

屈军锁， 侯晓宁， 张继荣， 樊永军

(1.西安邮电大学 通信与信息工程学院， 陕西 西安 710121; 2.电信科学技术第四研究所 研发部，陕西 西安 710061)

四基站时差和牛顿迭代法的三维定位算法

屈军锁1， 侯晓宁1， 张继荣1， 樊永军2

(1.西安邮电大学 通信与信息工程学院， 陕西 西安 710121; 2.电信科学技术第四研究所 研发部，陕西 西安 710061)

结合时差定位、球坐标系转换法和牛顿迭代法，针对四基站时差定位提出一种联合定位算法。利用时差定位和球坐标系与直角坐标系的转换关系对海面空中目标进行定位，分析不同布站方式对定位精度的影响，并以联合算法的结果作为牛顿迭代法的初值进行迭代。通过对目标在5 km高空匀速直线行驶40 km进行仿真，得到均方根误差小于45 m的定位精度。此方法不存在定位模糊或无解问题，且当目标与基站距离越大，其定位精度越优于最小二乘算法。

时差定位；牛顿迭代法；球坐标系转换；定位精度

时差定位(Time Different of Arrive, TDOA)系统具有定位精度高，抗干扰能力强，并且定位速度快等优点，因而在无源定位技术中得到广泛应用[1]。

TDOA定位系统在用四个基站进行定位解算过程中存在定位模糊或无解[2-3]，会影响定位的精度。消除定位模糊和无解问题的方法大致分为两类：一类通过添加辅助测量设备[4-6]消除定位模糊，而对定位无解情况只是假设目标高度进行处理；另一类则利用系统本身特征增加有效信息或参数函数，同样也可以消除定位模糊或无解，这类方法无需添加辅助信息，系统负担小。

球坐标系转换法[7]就属于第二类方法。利用直角坐标系和球坐标系的转换关系，可得出目标到主站的距离与主站到其它三个辅站的距离差的函数关系式，并且将函数关系式代入坐标转换关系中直接求出定位结果。运用时差定位和球坐标系转换法联合定位的精度要要优于单纯使用球坐标系转换法定位的定位精度。在用球坐标转换法求解目标到主站的距离与主站到其它三个辅站的距离差的函数关系式时，用到了辅站之间的夹角关系。当测向距离较大时，夹角之间的微小差距都会影响定位精度。但文[7]只验证了当目标距离基站较远的情况下的基于球坐标系转换法的定位精度，没有对近距离目标的定位精度进行仿真实现，也没有研究各辅站之间的夹角对定位精度的影响，对于提及的球坐标系转换法结合参变量法的方法也未加以仿真实现。

本文拟验证四基站时差定位算法和球坐标系转换法的联合算法对低空环境中目标的定位精度，分析基站间布站方式对定位精度的影响，并运用牛顿迭代法进一步提高目标的定位精度。针对联合算法在海面舰艇中的应用，系统安装四个雷达侦察设备，以其中一个设备为主站，其他三个设备为辅站，联立四基站TDOA时差定位算法和球坐标系转换法建立系统定位模型，对目标进行定位实现。

1 模糊和无解分析

无源时差定位根据多个测量站接收到辐射源信号并经过数据处理得到到达时间差，在三维空间中，两观测站的时间差确定了一对以这两个观测站为焦点的双曲面，目标至少需要三对独立的双曲面相交来定位，因而至少需要四个基站才能实现[8-10]。

假设无源时差定位系统由四个基站构成，主站的坐标为(x0,y0,z0)，三个辅站的坐标分别为(xi,yi,zi)(i=1,2,3)。对于四基站时差定位，设目标的空间坐标为(x,y,z)，令r0为目标与主站间的距离，ri(i=1,2,3)为目标与各辅站之间的距离，Δri表示目标到主站与到各辅站之间的距离差，c为光传播速率，Δti(i=1,2,3)表示目标到主站与到各辅站之间的时间差,则有定位方程组

整理上式得

(x0-xi)x+(y0-yi)y+(z0-zi)z=ki+r0Δri，

(1)

其中

式(1)可写成矩阵形式

AX=F,

其中

时差定位系统只有三个方程，却有x，y，z和r0四个未知量。若将r0看作已知量，当rank(A)=3时，目标的估计值

若令

则目标的估计位置为

(2)

其中

将式(2)所得目标估计值代入原方程式(1)，得到关于r0的一元二次方程

(3)

其中

通过求解关于r0的一元二次方程即可得目标位置的三维坐标。由式(3)可知，关于r0的一元二次方程不存在唯一解。当b2-ac=0时，方程存在唯一解；当b2-ac>0或b2-ac<0时，方程出现定位模糊或无解。

为了消除定位模糊，需要添加其他辅助测量信息或根据辐射源的先验信息进行处理，对于定位无解通常假定目标高度进行求解。事实上，利用球坐标系转换法即可达到消除定位模糊或无解的效果。

2 用球坐标系转换法消除模糊和无解

2.1 目标与主站间的距离

球坐标系与直角坐标系的转换关系如图1所示，其中M为空中目标所在位置，O为主基站，A，B，C分别为三个辅助基站，θ为辅站B与直角坐标系x轴的夹角，α,β分别为目标的俯仰角和方位角。假设φ1和φ2分别为A,B,C三个基站之间的夹角,主基站到A，B，C三个辅站的基线长度分别为Li(i=1,2,3)。OM为r0，MB为Δt2，根据球坐标插值法,对于△MOB可得关系式

化简可得

同理可得关于A站和C站关系式

若令

则可解得

(4)

图1 球坐标系与直角坐标系转换

2.2 消除定位模糊

对于四基站TDOA定位系统，如何消除定位模糊和无解一直是人们关注的主要问题。定位模糊是由于定位方程组的多值产生，而定位无解是因为定位方程组无解造成。因此，在基于球坐标转换法的方法中，当消除定位模糊时，结合式(4)，联立四基站TDOA定位方程组，可得

解此方程组，即可消除定位模糊，得到目标估计值。

2.3 消除定位无解

得到目标到主基站的距离r0后，根据球坐标系与直角坐标系之间的转化关系

(5)

再利用坐标旋转可得目标位置坐标

(6)

根据x，y，z和r0之间的关系,易得

(7)

定位无解是由于方程组本身造成，不能由上述定位方程组直接求得，而需要将式(4)代入式(5)(6)(7)进行计算，从而消除定位无解，得到目标的估计值。

只要知道目标到主站与到各辅站之间的时间差，得到时间差与r0的关系，利用球坐标转换法可以直接求出目标的三维坐标。不同的基站布局，只需调整不同的基线长度和基站间的角度。

3 球坐标系转换法中的布站方式

时差定位和球坐标系转换法联合定位可以调整基站间和夹角的基线长度，但是如果调整了基站间的角度和基线长度，会改变基站的布局方式，而不同的布局方式对定位精度产生影响[11-12]。

假设各基站时间测量误差为10ns，各基线长度均为50km，站址测量误差为2m，时间测量误差与站址测量误差的相关系数取0.3，定位高度为10km。根据本定位系统条件，主站为原点，因此对星形布站和三角形布站方式下的定位精度进行仿真，仿真结果如图2所示。

通过仿真结果可见，星形布站定位精度总体上优于三角形布站。星形布站中目标离主站越近定位精度越高，定位曲线近似等值圆分布；三角形布站的定位精度分布性较强，目标越靠近x轴，定位精度越高。因此，在运用球坐标系时，采用星形布站方式才能达到最好的定位效果，改变基站间角度虽然能够实现定位结果，但没有星形布站方式下的定位精度高。

(a) 星形布站

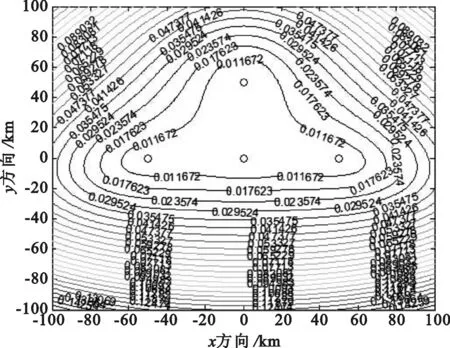
(b) 三角形布站

4 牛顿迭代法

在消除定位模糊和无解以及分析了布站方式对定位精度的影响后，将所得估计值作为牛顿迭代算法的初始值进行迭代，进一步提高目标位置估计的精确度。牛顿迭代法是一种使用梯度下降法进行迭代求解的算法[13]。首先，需要假设一个初始值，然后进行迭代估计，直至求得一个满足一定准则的估计解。初始值越接近真实值，则算法收敛性越好。因此，选取合适的初始值对保证算法收敛性及其收敛速度非常重要。根据牛顿迭代算法的条件，将所建立目标定位系统模型转换为

当其雅可比矩阵

为非奇异阵时，目标位置可表示为

5 算法仿真

无源定位系统对空中目标进行定位,其基站的布局方式对定位精度有很大的影响[14]。根据文献[15]，当目标的飞行方向或趋势不确定时，星形布站能达到更好的效果，因此选用星形布站方式。

在目标定位系统的仿真中，令主站及3个基站的坐标分别为

O(0,0,0)， A(26,15,0)，B(-26,15,0)， C(0,30,0)，

单位为km, 时间测量误差为10ns，基站间夹角

φ1=φ2=120°，

基线长度

L1=L2=L3=30km。

如图3所示，MN为目标的运行轨迹，在z轴5km左右处作匀速直线运动。对目标进行等分采样100次，为了验证本联合定位算法的效果，对目标轨迹进行均方根误差分析，结果如图4所示。定位误差小于45m，适于工程应用要求。

图3 目标的运行轨迹

图4 均方误差仿真分析

为了进一步分析该联合算法的性能，将其与最小二乘算法比较，对不同区域范围内的目标点进行算法仿真，计算其误差精度。表1为与最小二乘算法的定位算法精度比较结果。由表1可知，所给算法的定位精度可达到基于最小二乘TDOA算法的定位精度。

表1 两种定位算法精度比较

最小二乘算法是利用两次加权最小二乘法来获取目标的坐标位置，当噪声服从高斯分布时具有定位精度高和计算量小的优点。要实现最小二乘法定位至少需要五个基站，且它受时差测量误差影响大。所给算法z轴的定位精度始终高于最小二乘算法中z轴的定位精度。当目标与基站的距离越大时，所给算法的定位效果明显优于最小二乘算法。

6 结语

结合TDOA定位估计性好和牛顿迭代法收敛速度快的优点，验证了基于球坐标系转换下的TDOA定位算法和牛顿迭代法的联合算法对低空目标的定位情况，且使用球坐标转换法消除了四基站TDOA算法中的定位模糊和无解问题。通过仿真结果和数据分析证明，该算法可有效解决四基站TDOA对空中目标的三维定位问题，无需其他任何辅助信息，定位精度可信，且在目标距离基站越远的情况下定位效果越优于最小二乘算法。该算法计算量小，系统容易搭建，适于工程应用。本算法在不同基站布站方式下的定位精度有所不同，当系统为星形布站时定位效果最佳。

[1] 刘聪锋.无源定位与跟踪[M].西安:电子科技大学出版社,2011:11-18;207-230.

[2] 杨洁.空间四站时差定位算法及其性能分析[J].西安邮电学院学报，2012,17(2):13-16.

[3] 俞志强,叶朝谋.四站三维时差定位模糊分析[J].空军雷达学院学报，2009,23(5):370-372.

[4] 刘方正,祁建清,戚亚拯,等.高精度四站无源时差定位方法及精度分析[J].火力与指挥控制，2012,9，37(9):105-108.

[5] 吕晶晶,姚金杰.基于最小二乘和牛顿迭代法的空中目标定位[J].微电子学与计算机，2011，28(9):108-110.

[6] 王玲,魏星,万建伟,等.基于TDOA定位算法的模糊解消除方法[J].计算机工程与科学，2006,28(3):74-75.

[7] 陈双,赵宏忠.一种基于球坐标系的四站三维时差定位算法[J].现代防御技术，2011,39(1):133-137.

[8] 白菊蓉,高兴富.第五站对空间四站TDOA定位中的模糊影响[J].西安邮电学院学报，2007,12(1):12-15.

[9] 毛永毅,白菊蓉.空间四站时差定位中的模糊及无解研究[J]. 电讯技术，2006(6):53-57.

[10]LeiYanping,GongFengxun,MaYanqiu.Optimaldistributionforfour-stationTDOAlocationsystem[C]//2010 3rdInternationalConferenceonBiomedicalEngineeringandInformatics.Yantai:IEEE, 2010:2858-2862.

[11] 邴志光.运动多站时差无源定位系统关键技术研究[D].镇江：江苏科技大学，2012:5-10.

[12]YuHuagang,HuangGaoming,GaoJun,etal.Practicalconstrainedleast-squarealgorithmformovingsourcelocationusingTDOAandFDOAmeasurements[J].BIAISystemsEngineeringandElectronics,2012,23(4):488-494.

[13] 杨俊峰,张丕状.基于DTOA/DOA和牛顿迭代法的震源定位方法研究[J].地震研究，2012,36(3):324-329.

[14]HaraS,AnzaiD,YabuT,etal.AnalysisonTOAandTDOALocationEstimationPerformmancesinaCellularSystem[C]//2011IEEEInternationalConfefrenceonCommunications.Kyoto:IEEE,2011:1-5.

[15] 黄金凤,韩焱,王黎明.无源时差定位布站形式对定位精度的影响[J].火力与指挥控制，2009,34(10):33-35.

[责任编辑:瑞金]

3D localization algorithm based on 4-station time difference of arrival and Newton iteration

QU Junsuo1, HOU Xiaoning1, ZHANG Jirong1, FAN Yongjun2

(1.School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121,China)(2.Department of research and development, Fourth Research Institute of Telecommunications Technology, Xi’an 710061,China)

In order to solve the problem of ambiguity or no solution problem caused by the 4-station 3D localization algorithm and low accuracy of spherical coordinate transformation, a method combined with Time Difference of Arrival location, spherical coordinate conversion and the Newton iteration method is proposed. By using Time Difference method and spherical coordinate conversion time to locate the aerial targets on the sea, analyzing the positioning accuracy effect of different angle on auxiliary stations, and taking the joint algorithm results as the initial value of the Newton iterative method, the positioning accuracy of the system can be further improved. A Matlab simulation on the target at an altitude of 5 km of uniform motion in a straight line running 40 km is carried out and the positioning accuracy is achieved within 45 m. This method does not have ambiguity or no solution problem, and can effectively improve the positioning accuracy of the system. The greater the length between the target and the station, the better positioning accuracy can be achieved by this method compared to the least square algorithm.

time difference of arrival location, Newton iteration method, spherical coordinates transformation, positioning accuracy

2014-12-07

陕西省科技厅科学研究计划资助项目(2012K06-50)

屈军锁(1968-)，男，教授，从事宽带通信网络及信息化研究。E-mail:qujunsuo@xupt.edu.cn 侯晓宁(1988-), 女，硕士研究生，研究方向为通信网技术和应用。E-mail:ning56822@163.com

10.13682/j.issn.2095-6533.2015.02.008

TN957.52

A

2095-6533(2015)02-0036-05