预应力管桩反射波法的三维波场分析
2015-06-19刘东甲柯宅邦卢志堂刘华瑄
陶 俊, 刘东甲, 柯宅邦, 卢志堂, 刘华瑄
(1.合肥工业大学 资源与环境工程学院,安徽 合肥 230009; 2.安徽省建筑科学研究设计院,安徽 合肥 230001; 3.同济大学 岩土及地下工程教育部重点实验室,上海 200092)
预应力管桩反射波法的三维波场分析
陶 俊1, 刘东甲1, 柯宅邦2, 卢志堂3, 刘华瑄1
(1.合肥工业大学 资源与环境工程学院,安徽 合肥 230009; 2.安徽省建筑科学研究设计院,安徽 合肥 230001; 3.同济大学 岩土及地下工程教育部重点实验室,上海 200092)
文章建立了管桩的三维动力学模型,运用柱坐标下的弹性波动方程求解自由管桩的动力响应;利用交错网格有限差分法编制相应程序,通过数值计算得到桩身各点在不同时刻的振动速度;探讨了完整桩在竖向激振力作用下的瞬态动力响应,绘制管桩低应变动测的三维波场图;研究管桩的三维干扰效应,阐明了应力波在管桩中的传播理论,直观地显示管桩中除纵波外还存在横波和面波。模型桩实验实测曲线上的信号均能与数值模拟所得波场图一一对应,说明了数值模拟的正确性。文中还比较了不同纵向线上各点的干扰情况,直观地验证了90°为较理想的传感器安装点。
管桩;反射波法;有限差分法;三维波场
目前,在检测桩身完整性方面应用最多的方法是低应变反射波法,其理论基础为一维弹性杆纵波理论[1-3]。然而,管桩在低应变检测时,桩顶某一点受到低应变瞬态集中荷载的作用,桩身中应力波的传播是一个三维波动问题。利用低应变法反演管桩缺陷位置时,必须考虑管桩的三维效应以及波的各种频散作用,才能较大地减小误差[4]。过去研究应力波传播的三维效应问题大都采用有限单元法[5-6]。文献[7-8]用有限元对预应力管桩瞬态振动问题进行了研究,通过数值计算与实验,对激振方式、激拾振的位置关系进行了计算分析,对管桩完整性检测提出了指导意见;文献[9]对低应变中受瞬间冲击荷载作用的完整和缺陷PCC大直径薄壁混凝土管桩的动力响应进行了三维有限元模拟,详细研究了PCC桩低应变检测中的三维效应;文献[10]利用交错网格有限差分法求解三维弹性波动方程,得出了完整桩在瞬态竖向激振力作用下的动力响应;文献[7,11-12]利用有限差分法计算了低应变动测时三维自由管桩的振动问题,通过数值计算的结果证明了在管桩桩顶时域曲线上,测点处速度波第1峰对应的时间比激振点处有一定的滞后。上述成果丰富了管桩三维理论,但对于管桩三维波场的问题,尚需进一步研究。本文通过建立管桩的三维动力学模型,得到柱坐标下的弹性波动方程,利用交错网格有限差分法数值计算对应力波在管桩中的传播理论进行分析研究。
1 管桩低应变动测的三维动力学模型
将桩看作线弹性体,不计体力,运用柱坐标下的弹性波动方程求解自由管桩的动力响应。基本方程如下:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
其中,ρ为弹性体的密度;λ、μ为弹性体的拉梅系数;vr、vφ、vz为质点在各方向上的速度分量;Trr、Tφφ、Tzz、Trφ、Trz、Tφz为应力分量。
对于材料参数不连续的界面,通过调整网格使速度和剪应力的采样点刚好在界面上,计算点上与速度和剪应力对应的材料参数值可以用如下等效值来表示:
(10)
(11)
其中,ρ1、ρ2分别为计算点邻近2个采样点的质量密度;μ1、μ2、μ3、μ4分别为计算点临近4个采样点的剪切模量。
人工边界:由于波在桩中传播一个回程的时间很短,因此对于桩周土较软时可以采用远置人工边界,只要波还未传到边界处就可以满足条件。
初始条件:由于在激振力作用前,桩土系统处于静止状态,所以初始时刻,桩土质点的速度分量和应力分量均为0。
激振力作用范围为桩顶的一片圆形区域,对于桩顶边界条件,在激振力作用范围内有:
(12)
(13)
其中,rc=(ri+ro)/2,ri、ro分别为管桩内壁半径和外壁半径;r0为激振力作用半径;I、t0分别为激振力冲量和作用时间。
(14)
将 (1)~(9) 式和 (12)~(14) 式离散,并考虑到自由管桩内外桩壁和桩底面的应力边界条件,利用交错网格有限差分法编制相应程序。
数值模拟算例中计算基本参数如下:桩型为PHC-AB500(100),桩长7 m,泊松比为0.28,桩密度2 450 kg/m3,弹性模量52.975 GPa,激振力冲量1 N·s,激振力作用时间0.6 ms。计算网格参数如下:径向网格单元dr=0.01 m,竖向网格单元dz=0.06 m,时间单元dt=0.875 μs。
通过数值计算得到桩身各点在不同时刻的振动速度和受力状态,桩顶3个特定点的振动速度响应曲线如图1所示。
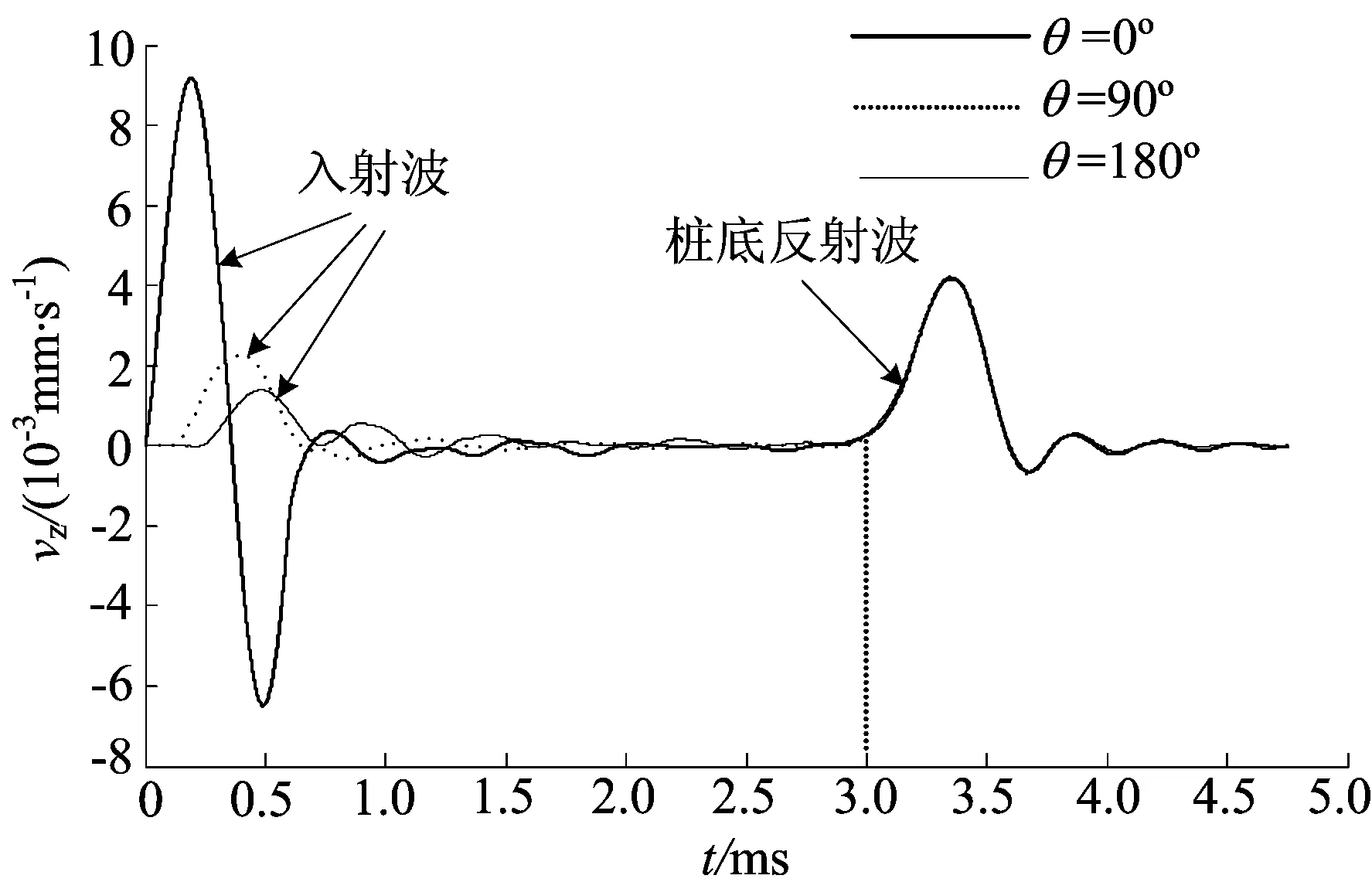
图1 桩顶不同位置的速度响应
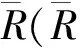
由图1可知传感器放在θ=90°位置时三维干扰较小; 第1个峰的初至时间不一致,其与敲击点处相比的滞后时间为td,td随θ的增大而增大; 曲线的第1个峰的幅值随θ的增大而减小;桩底反射几乎同时到达。
由于滞后时间和应力波的频散现象[13],选θ=0°曲线入射波和桩底反射波起跳点算得波速为4 667 m/s。
2 管桩低应变动测的三维波场研究
为了对应力波在桩身中传播的路径和规律进行直观地研究,根据上述所编制的程序,使用Matlab绘制了数值模拟桩体不同时刻的波场图,如图2所示。
图3所示为桩顶环向剖面示意图,考虑到图形的对称,将敲击点设在环向角度φ=180°点。

图2 不同时刻桩顶环向剖面的波场图
图2是在环向角度φ=180°点敲击时,对管桩三维模拟不同时刻桩顶环向剖面的波场快照图。t=0.5 ms时表示桩顶环向角度180°点位置已振动,波以此位置为中心以球面的形式向外传播。t=1.0 ms到t=2.0 ms, 波从桩顶向四周辐射,此时的波由球面逐渐向平面过渡,并传播至桩底。波在到达桩底界面时,转化为透射波与反射波,分别向桩外和桩内传播。t=2.5 ms到t=3.5 ms, 桩底反射波向上传播至桩顶,在3.5 ms左右时桩顶接收到桩底反射波。至此,波在桩中经历了一次往返传播。
为了分析在管桩中传播应力波的成分及最佳拾振点位置,分别考虑不同环向角度纵向线的波场图。不同环向角度纵向线示意图如图4所示。

图3 桩顶环向剖面示意图
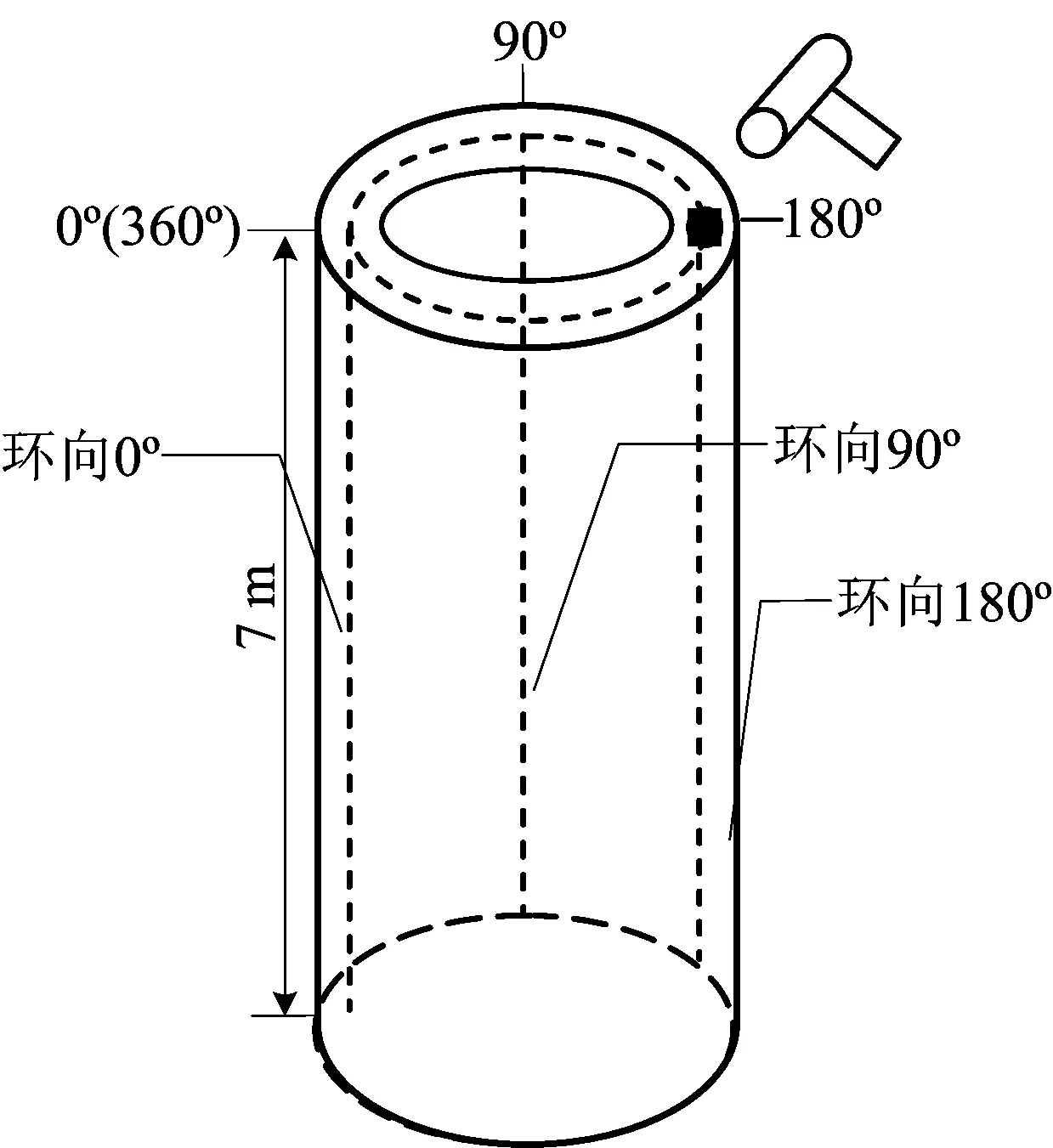
图4 不同环向角度纵向线示意图
在环向角度φ=180°点敲击时,不同环向角度纵向线的波场图如图5所示。
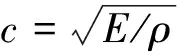
图5a中2 m线与时距曲线交于R1、R2处,图5c中2 m线和5 m线分别与时距曲线交于P1、P2、P3,S1、S2、S3处。在图5a和图5b中时距曲线1的起始端与时距曲线1的斜率不一样,可以看出离敲击点处越远的纵向线上,起始端的斜率与时距曲线1的斜率偏离越大,这是由于面波所引起的。
文献[7]通过桩顶几个点振动曲线的对比,得出与激振点成90°的桩顶拾振点更容易消除或减弱高频干扰,是较理想的传感器安装点。笔者根据图5b,得出90°纵向线上各点的干扰均较小。因此,由以上不同环向角度下的波场图对比分析可以看出,在90°纵线各点,波的干扰最小,信噪比最高。
为了研究管桩低应变检测中的三维效应,分别考虑不同深度环线的波场图。竖向不同深度处环向线示意图如图6所示。
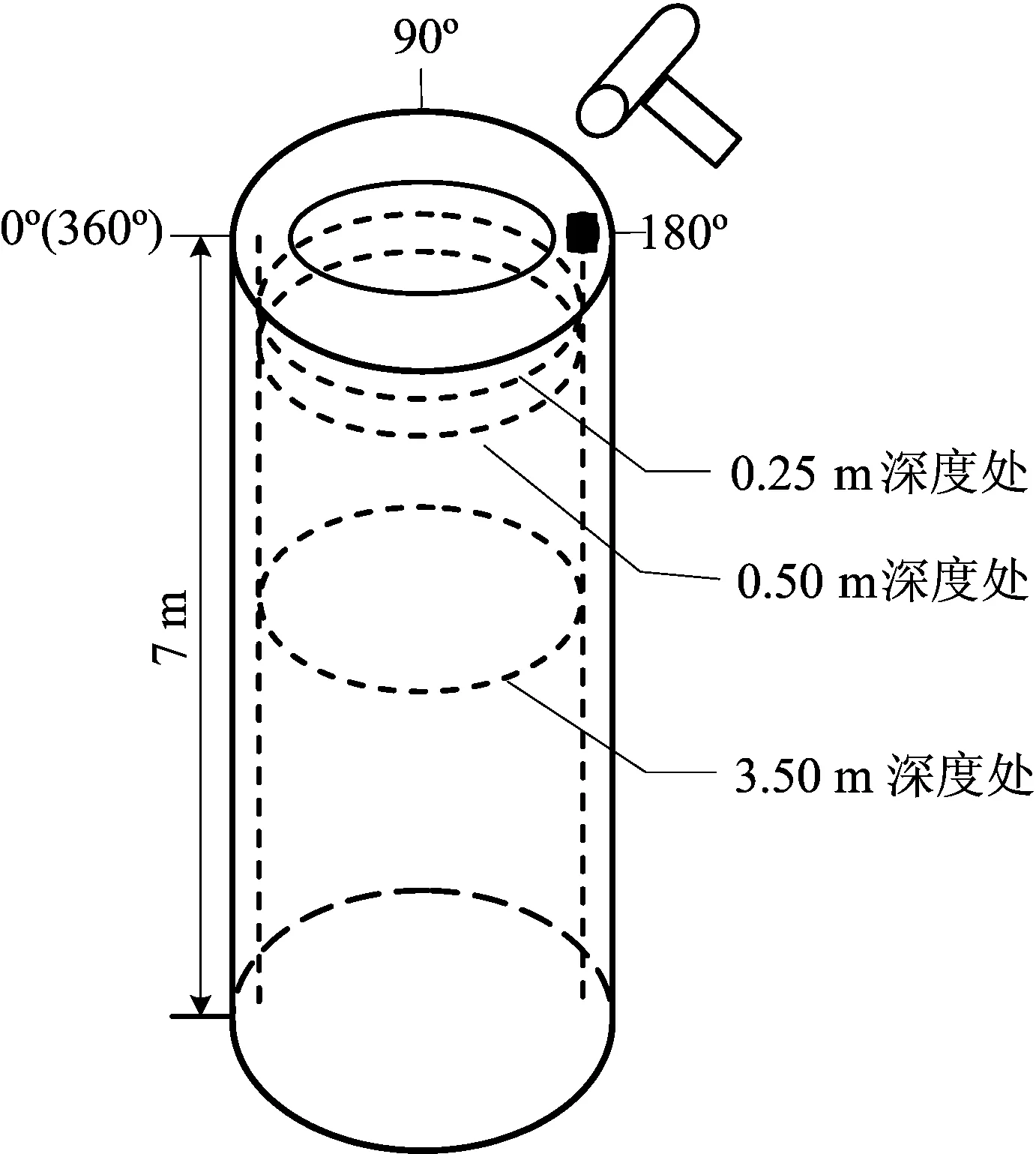
图6 竖向不同深度处环向线示意图
在环向角度φ=180°点敲击时,竖向不同深度处环向线的波场图如图7所示。

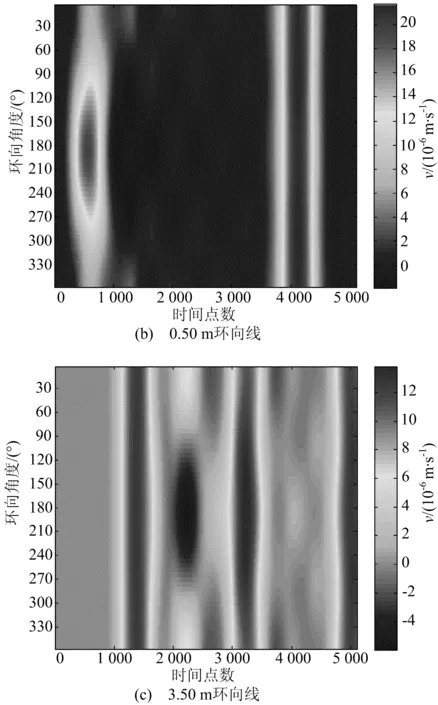
图7 不同深度环向线的波场图
图7a中在敲击点处,应力波是最先到达且能量最大,其他位置上稍有延迟,可以很明显地看到应力波在管桩中是以敲击点为中心位置以球面的形式向外传播,管桩的三维效应明显,直观地说明了图1中滞后时间td的存在。在图7c中,应力波到达不同环向角度位置的时间基本相同,各点处的振动速度也基本相同,因此大于某深度的波动问题可以满足平截面假定,将其简化为一维波动问题,此深度即为文献[14]提及的平截面假设影响深度,该深度与激振力的特征波长和桩径有关。
3 模型桩实验
对安徽省建筑科学研究设计院的完整模型桩进行试验,模型桩桩型为PHC-AB500(100),即外直径500 mm、壁厚100 mm的预应力混凝土管桩,桩长7 m。在桩顶敲击,敲击点正下方5 m处采集数据,得到实测曲线与数值模拟所得理论曲线进行对比,如图8所示。
由图8可以看出,理论曲线和实测曲线吻合较好;参照图5c分析图8,可见,S1为杆波传播到5 m处的信号,S2为杆波传播到桩底经桩底反射到5 m处的信号,S3为横波信号。该实测曲线验证了图5所述的时距曲线2即为横波在桩中的传播。
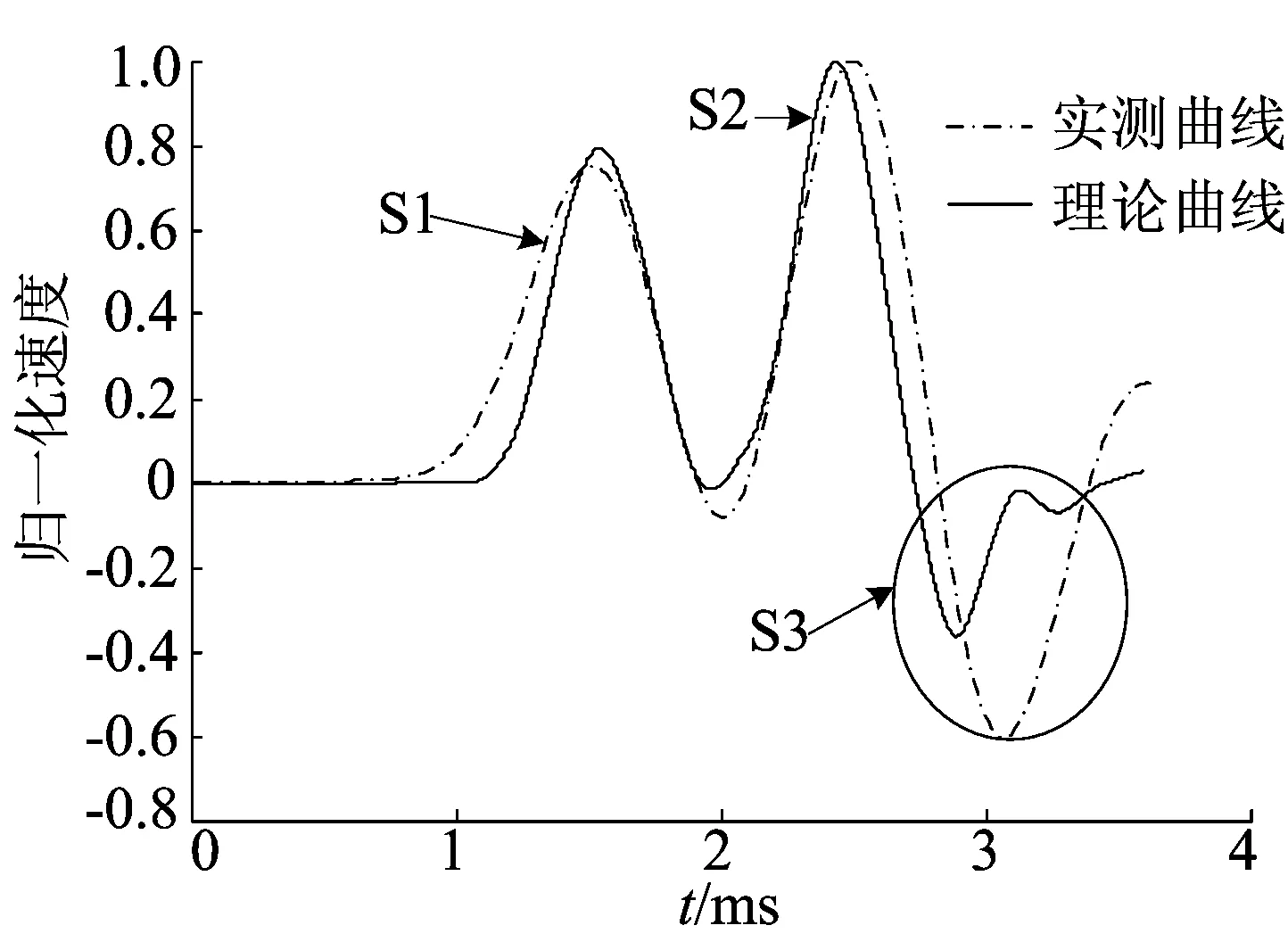
图8 实测和理论拟合曲线
在桩顶敲击,分别在敲击处正下方2 m和正下方 2 m关于轴线对称点处采集数据,得到的2条实测曲线如图9所示。

图9 模型桩实测曲线
图9中R1、P1分别为杆波传播到2 m处这2个点接受的信号,P2、P3、R2为横波信号,在图5a、图5c中也能清晰地看见,R3、P4为杆波传播到桩底经桩底反射到2 m处的信号。实测曲线上的信号均能与数值模拟所得波场图一一对应,说明了本文数值模拟的正确性。2条曲线的第1个峰值初至时间不一致,说明应力波到达管桩同一深度2 m处不同接受点的时间不同,体现了管桩中三维效应的存在;同一横截面上,横波使各质点的振动速度不一样,对于横波在管桩中的传播还需作进一步研究。
4 结 论
(1) 从不同环向角度下的波场图可知,激振点和拾振点呈90°时,波的干扰最小,信噪比最高,直观地说明了90°为较理想的传感器安装点,且90°纵向线上各点的干扰均较小。
(2) 由不同纵向线的波场图知,在桩顶敲击后,离桩顶面下一定范围内,均有面波的影响。
(3) 在桩身深度较浅的同一环向线位置上,应力波到达不同角度位置的时间是不同的,其中在敲击点φ=180°处是最先到达的,其他位置上稍有延迟;当应力波传播到一定深度时,同一环向线位置上,应力波到达不同环向角度位置的时间基本相同,各点处的振动速度也基本相同,因此大于某深度的波动问题可以满足平截面假定,将其简化为一维波动问题。
(4) 应力波在管桩中的传播除纵波外还能明显地发现横波的存在,因此对于横波在管桩中的传播还需作进一步的研究。
[1] 刘东甲.不均匀土中多缺陷桩的轴向动力响应[J].岩土工程学报,2000,22(4):391-395.
[2] 徐攸在.桩的动测新技术[M].第2版.北京:中国建筑工业出版社,2003:33-45.
[3] Finno R J, Gassman S L. Impulse response evaluation of drilled shafts[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(10): 965-975.
[4] 陈 凡,徐天平,陈久照,等.基桩质量检测技术[M].北京: 中国建筑工业出版社,2003: 132-135.
[5] 黄大治,陈龙珠.钢筋混凝土管桩反射波法的三维有限元分析[J].岩土力学,2005,26(5):803-808.
[6] Chow Y K,Phoon K K, Chow W F,et al. Low strain integrity testing of piles:three-dimensional effects[J].Journal of Geotechnical and Geoenvironmental Engineering,2003,129(11):1057-1062.
[7] 陈 凡,罗文章.预应力管桩低应变反射波法检测时的尺寸效应研究[J].岩土工程学报,2004,26(3):353-356.
[8] 罗文章.管桩在低应变瞬态集中荷载作用下的速度响应研 究[D].北京:中国建筑科学研究院,2002.
[9] 费 康,刘汉龙,张 霆.PCC 桩低应变检测中的三维效应[J].岩土力学,2007,28(6):1095-1102.
[10] 卢志堂,刘东甲,龙丽丽,等. 基桩低应变检测三维问题的数值计算[J]. 合肥工业大学学报:自然科学版,2011,34(6):905-909.
[11] 柯宅邦,郭 杨.低应变检测管桩缺陷位置的三维反演分析[J].四川师范大学学报:自然科学版,2011,34(6):181-183.
[12] 卢志堂,王志亮,刘东甲,等.管桩低应变检测中的三维效应分析[J]. 同济大学学报:自然科学版,2012,40(11):1603-1607.
[13] Cobos C, Han D H. Velocity dispersion estimation[C]//Expanded Abstracts of SEG 76th Annual International Meeting,2006:2309-2312.
[14] 陈 凡,王仁军.尺寸效应对基桩低应变完整性检测的影响[J].岩土工程学报,1998,20 (5):92-96.
(责任编辑 张淑艳)
Application of reflected wave method to 3-D wave field analysis of prestressed pipe piles
TAO Jun1, LIU Dong-jia1, KE Zhai-bang2, LU Zhi-tang3, LIU Hua-xuan1
(1.School of Resources and Environmental Engineering, Hefei University of Technology, Hefei 230009, China; 2.Anhui Institute of Building Research and Design, Hefei 230001, China; 3.Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China)
Three-dimensional dynamics model of pipe pile is established, and the elastic wave equations under cylindrical coordinate system are used to solve the dynamic responses of free pipe piles. The staggered grid finite difference method is used to prepare the corresponding procedures, and the numerical calculation is carried out to obtain the vibration velocity of pile points at different moments. The transient dynamic responses of a pipe pile subjected to transient vertical loading are discussed. The three-dimensional wave snapshots of low strain dynamic testing of pipe piles are drawn, and the three-dimensional interference effects of pipe piles are studied, so as to expound the transmitting theory of the stress wave in the pipe pile. It is shown visually that the shear wave and surface wave exist in the pipe pile besides the longitudinal wave. According to the model pile testing, the signal on the measured curve can one-to-one correspond with the wave snapshot obtained by the numerical simulation, thus proving the correctness of the numerical simulation in this paper. The interference of each point along different vertical lines is compared, and it is verified visually that the installation point of 90° which is the central angle of click vibration point and pick-up point for sensor is better.
pipe pile; reflected wave method; finite difference method; three-dimensional wave field
2014-02-19;
2014-04-09
住房和城乡建设部科技计划资助项目(2010-K3-23);广东省公路管理局科技资助项目(粤公研2011-21)
陶 俊(1990-),男,湖北监利人,合肥工业大学硕士生; 刘东甲(1957-),男,安徽枞阳人,合肥工业大学教授,硕士生导师.
10.3969/j.issn.1003-5060.2015.02.019
TU473.16
A
1003-5060(2015)03-0226-06
