基于SV模型的VaR Monte Carlo模拟

马 跃， 李金玉

（中国矿业大学 理学院，江苏 徐州 221116）

0 引 言

VaR（Value at Risk）即风险价值，目前作为很多金融机构从事风险管理的重要指标。金融资产往往具有波动聚集性，SV模型能很好地描述金融资产这一特征。近年来，很多学者对SV模型进行了研究，文献［1］将SV模型用于VaR的计算并与GARCH 模型相比较；文献［2］采用GARCH模型和SV模型对深圳股市进行了比较。结果表明，SV模型更能刻画金融市场的实际特征，且基于SV模型计算的VaR精确度更高。另外，从计算VaR的方法来看，主要有历史模拟法、分析法、Monte Carlo模拟法等。对于用Monte Carlo模拟法计算VaR已有很多文献进行了研究，如文献［3］的基于GARCH模型的风险价值蒙特卡罗模拟等，实践表明，用Monte Carlo模拟法计算VaR有许多优点。

然而，就目前的文献来看，将SV模型和计算VaR的Monte Carlo模拟法相结合的研究并不多；同时可以发现，在利用SV模型计算风险价值时，人们往往侧重于使用分析法［1－2］，而利用分析法计算VaR时，需要假定市场因子服从某种分布，这种假定会给VaR的计算带来一定的误差。而当使用Monte Carlo模拟法计算VaR时，则不需要假定市场因子的分布，这就在一定程度上减少了VaR的计算误差。

因此，基于以上原因，本文试图将SV模型与计算VaR的Monte Carlo模拟法相结合，并结合上证综合指数的风险价值进行实证分析。

1 VaR定义及Monte Carlo模拟法

VaR（Value at Risk）风险价值也称在险价值［4－5］，它描述了在一定的置信水平下，某一资产或投资组合在未来的一段时间内可能遭受的最大损失，可表示为：

其中，Pr为概率测度；ΔP为资产或资产组合在未来持有期Δt内的损失；α为显著性水平。VaR主要计算方法中的 Monte Carlo模拟法［5－6］也叫随机模拟法，是计算VaR的各种方法中较为有效的方法，其基本思路是通过反复大量地模拟金融变量的随机过程，使模拟值包括大部分可能情况，这样通过模拟就可以得到组合价值的近似分布，在此基础上就可求出VaR。基于Monte Carlo方法计算VaR的具体步骤如下：

（1）选择随机模型。本文选择几何布朗运动（GBM），它是股票价格变化中最为常用的模型之一，假定资产价值的变化在时间上是不相关的，其离散形式可表示为：

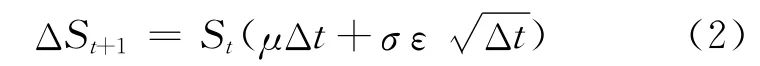
其中，ΔSt＋1＝St＋1－St；St为t时刻的资产价格；μ为资产收益率的均值；σ为资产收益率的波动率；ε为随机变量。

（2）随机模拟价格走势。定义t为当前时刻，T为目标时刻，利用t时刻对T时刻的价格进行模拟。为了模拟随机变量S的价格走势，记τ＝T－t是模拟的时间间隔，令Δt＝τ／n，从当前的价格St出发，按i＝1，2，…，n的顺序，根据产生的随机数εi再结合（2）式，利用递推法就能模拟出随机变量S 的未来价格走势（St＋1，St＋2，…，St＋n）以及计算目标时刻T时的价格ST。

（3）估计VaR。多次重复步骤（2），重复次数k越多越接近真实分布，这样就可以得到目标时刻T时的一系列资产的价格，在给定的置信水平c下，VaR即为在k次模拟结果中，将模拟价格按升序排列后第k（1－c）个模拟价格的损失。

2 Monte Carlo－SV－VaR 模型

SV模型即随机波动率模型［7］，是由Taylor在1986年提出的，其模型表达式可以表示为：

其中，yt为消去均值后第t期的收益；θt为对数波动；｛εt｝、｛vt｝为相互独立的；φ1为持续性参数。当｜φ1｜＜1时，上述SV模型是协方差平稳的。因金融资产或投资组合的收益率往往存在波动率“聚集效应”，大量的研究结果表明SV模型对收益率波动性的刻画能力较强，故本文选择SV模型对所选数据进行分析拟合。

假设当收益率分布服从正态分布时，可以推出VaR的计算公式［3］为：

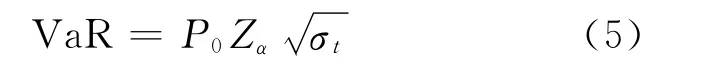
其中，P0为资产初始时的价格；Zα为正态分布分位数；σt为条件方差。

结合SV模型和（5）式即可求出 VaR，将（3）～（5）式记为SV－VaR模型。

假设收益率分布服从正态分布往往具有局限性，会给VaR计算结果带来一定的误差，为了克服这种影响，引出 Monte Carlo－SV－VaR模型，其计算VaR步骤同一般的Monte Carlo计算VaR类似，改变之处在于利用SV模型将（2）式中的资产收益率的波动率σ转化为条件标准差，具体形式如下：

然后利用Monte Carlo模拟法的步骤即可计算出VaR。

为了使计算出的VaR结果具有比较性，分别利用SV－VaR模型和 Monte Carlo－SV－VaR模型进行实证分析，并比较它们的精确度。

3 实证分析

3.1 模型建立

本文选取上证综合指数为研究对象，选取数据分析的时间段为：2008年11月25日到2013年6月28日，观测值个数为1112。本文主要利用的软件有Eviews6.0、Matlab7.0 和 WINGBUGS14。

在对SV模型进行参数估计的过程中，采用基于贝叶斯的马尔可夫链蒙特卡罗（MCMC）方法，在用MCMC方法估计参数时，使用文献［7－8］所假设的先验分布进行Gibbs抽样，先对每个参数进行20000次迭代，进行退火，以保证参数的收敛性，然后舍弃原来的迭代再进行20000次的迭代，对模型进行模拟仿真。本文采用对数收益率作为股票的日收益率，其计算公式如下：

其中，St为当日指数收盘价；St－1为前一日指数收盘价。

模型建立前先对上证综合指数进行统计分析，结果如图1、图2所示。

图1 对数收益率的柱形统计图

图2 正态QQ图

计算可知，对数收益率序列的JB统计量为222.6709，P值为0，偏度为－0.391753小于0，峰度为5.048485，结合图1、图2可判断出上证综合指数具有“左偏尖峰厚尾”特征，若用（5）式计算VaR则可能会带来一定的误差。

进一步绘出了上证综合指数对数收益率的线性图，如图3所示。

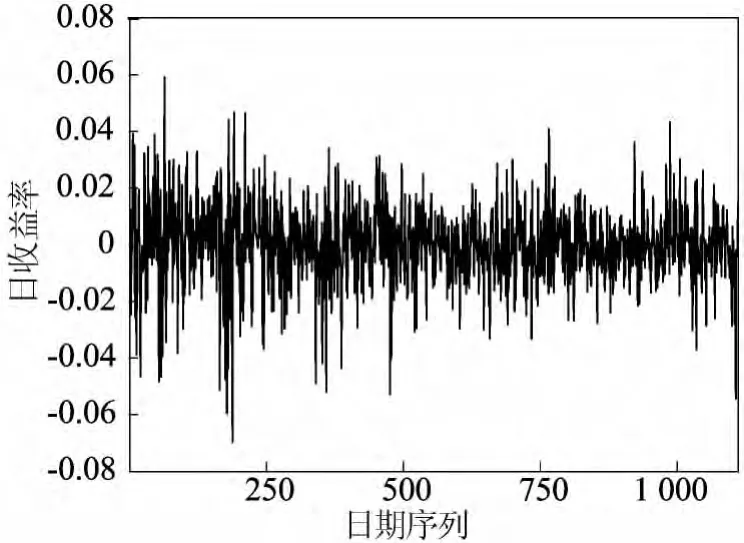
图3 上证综合指数对数收益率

由图3可以看出，上证综合指数对数收益率存在明显的波动率“聚集现象”，因此用SV模型可以刻画上证综合指数的收益率。使用WINBUGS14估计SV模型的结果如下：

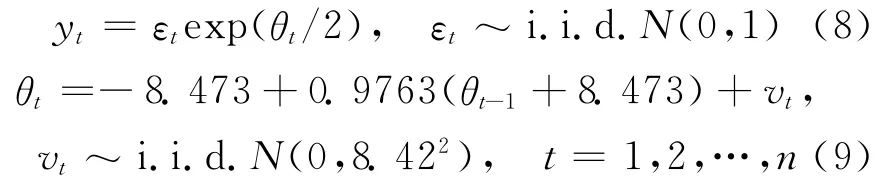
由模型的估计结果可以看出，持续性参数φ1值接近于1，表明上证指数具有很强的波动持续性，且φ1值大于0.96，由此进一步说明上证综合指数波动的聚集性，综合分析可知上述模型对上证综合指数具有很好的拟合效果。

3.2 SV－VaR模型计算结果及分析

本文选取的置信水平为95%，预测天数为510d。利用上述模型估计2011年5月20日的条件方差并结合（5）式求出在95%置信水平下的VaR值为28.98，同理可以求出直到2013年6月28日共510个交易日的VaR值，将VaR预测值（用SV－VaR代表）与真实损失（用SUNSHI代表）进行比较，结果如图4所示。

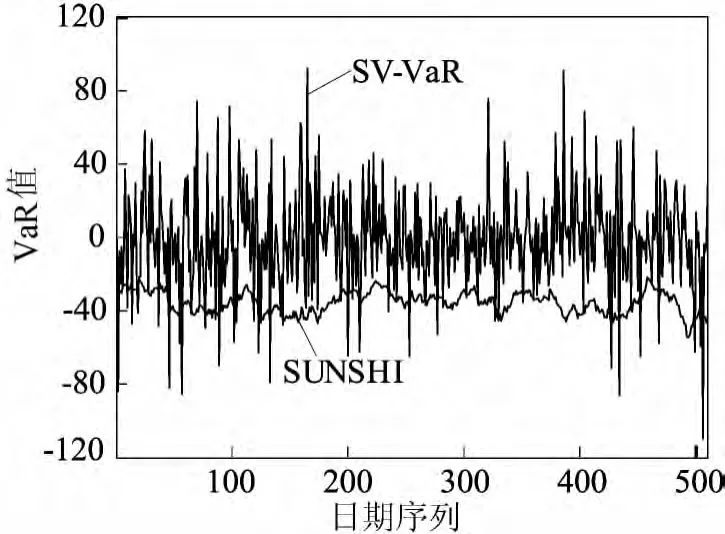
图4 用SV－VaR代表的VaR预测值与用SUNSHI代表的真实损失比较结果

进一步，可以确定VaR的失败次数为N＝40，失败率为7.8%，再利用文献［5，9］提出的失败频率检验法的接受域，即概率水平p＝0.05时，失败次数N的接受域（T＝510）为：

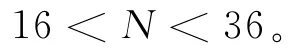
3.3 Monte Carlo－SV－VaR 模型计算结果及分析

将一天的持有期平均分为24个相等的时间段，Δt＝1／24，St代表初始时刻t的收盘价（这里从2011年5月19日开始），然后模拟下一时刻的收盘价，从而计算出VaR值，具体步骤如下：

（1）估计均值和条件标准差。使用2008年11月25日到2011年5月19日这602d的上证综合指数估计其均值μ，利用估计出来的SV模型估计2011年5月20日的条件标准差

（2）产生随机数。利用Matlab7.0产生24个服从标准正态分布的随机数ε1，ε2，…，ε24。

（3）模拟价格变化的可能路径。将步骤（1）、步骤（2）得到的均值μ、条件标准差和Δt代入（6）式，递推可以得到St＋1，St＋2，…，St＋24为收盘价格变化的一条可能路径，ST＝St＋24为2011年5月20日的一个可能的收盘价格。

（4）计算 VaR 值。重复步骤（2）、步骤（3）10000次，得到上证综合指数10000个可能的收盘价格。对按升序排列，找到下方5%的分位数，则可以计算出95%的置信水平下的可得出2011年5月20日上证综合指数置信水平为95%下的VaR为46.3。

同理利用Monte Carlo模拟法可以模拟出2011年5月20日到2013年6月28日上证综合指数连续510个交易日的VaR值。将VaR预测值（用MC－SV－VaR代表）与真实损失（用SUNSHI代表）进行比较，结果如图5所示。

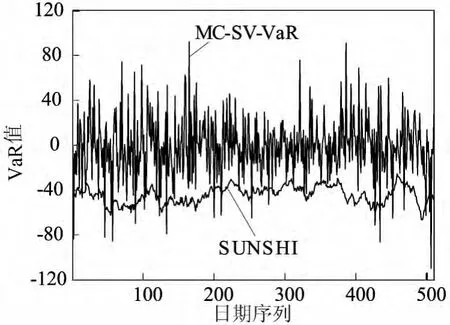
图5 用MC－SV－VaR代表的VaR预测值与用SUNSHI代表的真实损失比较

同样，可以确定VaR的失败次数N＝26，当T＝510，在95%置信水平下，失败次数N在区间（16，36）内，且失败率为0.05098，约为0.05，从而表明Monte Carlo－SV－VaR模型对上证综合指数VaR的预测效果非常理想。

4 结束语

本文利用SV模型对上证综合指数进行拟合，分别采用SV－VaR 模型和 Monte Carlo－SVVaR模型对风险价值进行预测，结果表明SVVaR模型计算的VaR值过于保守，低估了损失发生的概率，这可能是因为结合（5）式计算VaR值时需要假设收益率服从正态分布，而对数据进行统计分析时发现上证综合指数收益率具有“尖峰厚尾”特征，若用（5）式计算VaR值势必对VaR计算结果产生一定的误差；而利用Monte Carlo－SV－VaR模型计算VaR值时无需假设收益率服从何种分布，而是通过Monte Carlo模拟法模拟资产的近似真实分布，这种方法适用于任何分布的VaR值计算，且计算结果较为准确。本文利用Monte Carlo－SV－VaR模型计算VaR值的失败率为0.05098，接近于0.05，且失败次数 N＝26在Kupiec失败频率检验法的置信水平为95%、T＝510d的非拒绝域（16，36）之内，这表明利用Monte Carlo－SV－VaR模型计算上证综合指数VaR值的准确性较高，且与文献［1］的基于GARCH模型和SV模型的VaR比较，文中利用分析法得到的VaR值的失败率更加接近0.05，因此在收益率分布不确定的情况下，利用Monte Carlo－SV－VaR模型计算VaR值的精确度较高。当然也可以利用Monte Carlo－SV－VaR模型对汇率、原油价格等的VaR值进行计算，进一步确定其适用范围。

［1］余素红，张世英，宋 军.基于GARCH模型和SV模型的VaR比较［J］.管理科学学报，2004，7（5）：61－66.

［2］王宇新.GARCH模型和SV模型对深圳股市的比较［J］.合肥工业大学学报：自然科学版，2007，30（6）：743－745.

［3］陈 磊，任若恩，张金宝.基于GARCH模型的风险价值蒙特卡罗模拟［J］.系统工程，2006，24（7）：57－61.

［4］Jorion P.Risk：measuring the risk in value at risk［J］.Financial Analysts Journal，1996，52（6）：47－56.

［5］菲利普·乔瑞.风险价值VAR［M］.张海鱼，译.北京：中信出版社，2010：105－350.

［6］郭 繁.基于蒙特卡罗模拟法的风险价值（VaR）及其在中国股票市场中的应用［D］.山东：山东大学，2006.

［7］朱慧明，林 静.贝叶斯计量经济模型［M］.北京：科学出版社，2009：153－157.

［8］Meyer R，Yu J.BUGS for a Bayesian analysis of stochastic volatility Models［J］.The Econometrics Journal，2000，3：198－215.

［9］Kupiec P H.Techniques for verifying the accuracy of risk measurement models［J］.The Journal of Derivatives，1995，3：73－84.