柔性生产中基于人员任务匹配度的人员调度

赵亚玲, 葛茂根, 扈 静, 张铭鑫, 张 玺

(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)



柔性生产中基于人员任务匹配度的人员调度

赵亚玲, 葛茂根, 扈 静, 张铭鑫, 张 玺

(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)

文章针对单件小批量生产的柔性生产方式,考虑操作人员技能的多样性和对于不同任务技能水平的差异性等特点,根据操作人员对各任务的累计工作时间计算任务人员之间的匹配度,在此基础上建立柔性生产中资源受限下人员调度数学模型;通过启发式算法得到模型的初始解,并运用改进的遗传算法对模型进行求解,得到最优的人员调度方案以实现任务总完成时间最小的优化目标;最后结合具体实例验证了该求解模型的准确性与可行性。

柔性生产;人员调度;遗传算法;匹配度;资源受限

随着全球化和竞争的加剧,企业之间的竞争开始转向基于时间的竞争和基于顾客需求的竞争,为了适应日趋激烈的市场竞争,基于订单生产的单件、小批量的柔性生产方式成为主流,订单生产使得产品的种类、产量与生产时间的波动性特别大,操作人员要在顾客期望交货期内完成多种零件和产品的加工,不同任务有不同的能力需求,每个操作人员有不同的操作技能,且不同技能的能力水平不同。不同的人员配置方案直接影响任务的完成质量和完成时间。因此,对于基于订单生产的柔性生产,需要全面考虑人员的技能种类和技能水平,构建合理的人员配置方案,以实现在最短交货期内满足客户需求。

目前国内外围绕人员优化配置问题展开了大量的研究工作并取得了不少研究成果。例如，文献[1] 以合理的人工分配方案和最佳作业排序为目标建立了数学模型,采用遗传算法和动态规划法获取最佳的人工分配方案；文献[2]针对人员多技能情况,采用岗位适应度表示人员执行装配作业的能力,建立了以人员岗位适应度最大和装配线各工位之间作业人员岗位适应度差异最小为目标的装配线人员优化配置模型；文献[3]针对单元制造系统的操作工分配问题,在传统只考虑技术技能的基础上,增加了操作工人技能的提高,以最大化企业绩效为目标建立了混合整数规划模型。

以上研究都考虑到操作工的作业能力,部分学者还考虑到员工学习性,但未涉及不同能力水平和学习性对任务执行时间的影响。本文在总结前人研究的基础上,根据任务特点和操作工能力计算操作工与任务之间的匹配度[4],以最小化任务总完成时间为优化目标,构建柔性生产中人员优化配置模型[5],通过启发式算法得到模型的初始解[6],并运用改进的遗传算法对模型进行求解,得到最优的人员调度方案以实现任务总完成时间最小的优化目标。

1 人员与任务匹配度的计算

20世纪30年代美国康乃尔大学的莱特博士首先在航空科学期刊上提出了学习曲线。波音公司发现每一架飞机的工时消耗在前一架制造完成后都会有所下降,而且还是以一个可预测的比例下降。学习曲线反映了操作人员对某一项重复性工作干的时间越长,对该项工作的熟练程度就越高,即其从事该工作的工作技能水平越高。基于此,本文将第i个操作人员Pi对编号为j的操作任务Tj的匹配度的计算公式表示如下:

其中,PTij表示编号为i的操作工与编号为j的操作任务之间的匹配度;i=1,2,…,m;j=1,2,…,n;ti表示给定时间段内人员Pi的累计工作时间;tj表示达到任务Tj的标准需求值需要的累计工作时间。

2 人员调度的数学模型

2.1 问题描述

针对柔性生产制造企业,有n个工件由m个操作人员完成;工件Tj由qj个具有次序约束关系的不重叠工序组成,即每道工序需在其紧前工序完成后才能开始,不同工件之间的工序之间没有约束关系;每道工序的加工需要特定的技能,每道工序可由满足匹配度的任一员工加工;每个员工在同一时间最多处理一道工序,每个员工具有1种或多种技能,每种技能的水平不同,因而处理不同的可处理工序的效率不同;优化目标是要确定最优的的人员调度方案以实现最小化工序最大完工时间的优化目标[7]。

2.2 模型假设

(1) 假设操作工更换工序时,不考虑调整时间。

(2) 假设每一道工序时间足够短,操作工在执行该工序期间匹配度不变。

(3) 假设操作工一旦开始加工某道工序,该道工序完成之前不会中断。

(4) 假设人员和工序之间是一一对应关系,可以通过调整工序的粒度,使得每道工序只由1个人员执行,同时人员在同一个时刻只负责1道工序的加工。

2.3 定义模型变量

人员集为P={P1…Pi…Pm},m为人员数。

工作集为T={T1…Tj…Tn},n为工件数,工件Tj是由qj个具有次序约束关系的不重叠工序组成,Tj={Tj1,…,Tjk,…,Tjqj},且Tj={Tj1≤Tjk≤Tjqj}。

Qjk为工序Tjk的任务量,在生产中以其所需工时数具体量化,j∈T,k∈Tj。

Tsjk为工序Tjk的开始时间,j∈T,k∈Tj。

技能集合为S={1,…,g},g为所有技能种类。

Sjk为工序Tjk需要的技能,j∈T,k∈Tj。

Pjk为有技能处理工序的员工集合,j∈T,k∈Tj。

Si为员工Pi具有的技能集合,i∈P。

TBjk为工序Tjk的紧前工序集合,j∈T,k∈Tj。

PTijk为将操作工Pi分配至工序Tjk的匹配度,i∈P,j∈T,k∈Tj。

tjk为工序Tjk的预期执行时间,j∈T,k∈Tj。

2.4 人员调度的数学模型:

模型目标函数和约束条件如下:

(1)

(2)

(3)

(4)

目标函数(1)式是最小化工序最大完工时间;约束条件(2)式规定了参数tjk的计算方法;约束条件(3)式保证每个员工同一时刻只能处理1道工序,A(t)表示[t-1,t]内正在执行的任务集合;约束条件(4)式保证工序间的优先约束关系,即每道工序必须在其紧前工序完成后才能开始。

3 优化算法

柔性生产过程人员调度问题是一个复杂的离散型优化问题,和Job-shop调度问题一样是NP问题,本文采用改进的遗传算法对其进行求解,采用启发式算法产生遗传算法的初始种群。

3.1 初始种群

首先根据工序间的时序约束,随机选择开始时间最早的工序Tjk,确定该工序需求的技能集合Sjk,然后根据已经计算出的人员-工序匹配度确定有技能处理该工序的员工集合Pjk,优先选择与该工序匹配度大的操作人员;以此类推,建立人员-工序配置矩阵。

3.2 编码设计

采用实数编码法,对于一个有N道工序数的人员调度问题,其染色体由N个基因组成,每个基因由一个两位数表示,包含了工件—工序—时间—操作工的约束[8]。第1位数代表要加工的工件序号,同一工件的所有工序采用同一工件序号表示,根据它们在染色体排序中的顺序决定它们在不同机器上的加工顺序,每个工件序号出现的次数为该工件的工序数,第α次出现代表该工件的第α道工序;第2位代表加工该工序的操作工编号。以3个工件3个操作工,每个工件3道工序为例,其某一染色体为[12 23 13 31 12 23 32 21 33],其中第1个基因“12”表示第1个工件的第1道工序由第2个操作工加工,第3个基因“13”表示第1个工件的第2道工序由第3个操作工加工。

3.3 交叉算子设计

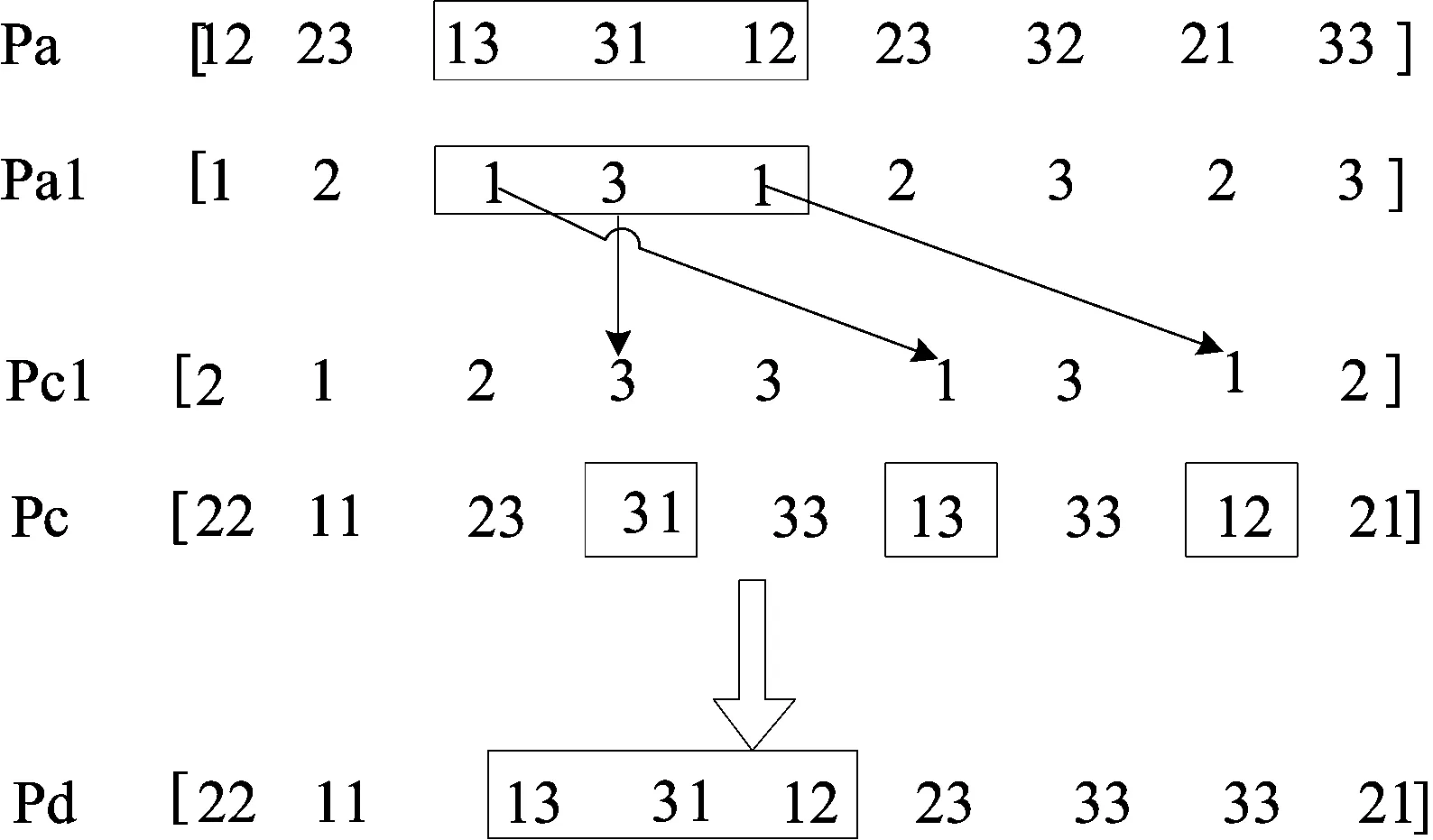
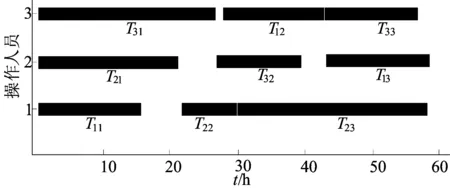
交叉策略采取二次交叉算子方式,交叉后既要得到操作工与工序之间的对应关系,还要得到工序的排序信息。染色体编码是基于工序排序的,因此需精心设计遗传算子以保证经过交叉后产生的子代是可行解。交叉算子设计如下:任取父染色体Pa中2个交叉点与母染色体Pb进行交叉操作,设为p1和p2(p1

以3个工件(每个工件3道工序),3个操作工为例,第1次交叉如图1所示:A(A1,A2,A3)表示这3个工件,工件A第α次出现表示工件A的第α道工序,基因的第2位数字M表示A工件的第α道工序由第M个操作工加工。在Pb中找到复制段中的第1位数字是A且第α次出现的数字的基因,将该数的第2位数字换为与A对应的M直到复制段的最后一个数。

图1 第1次交叉示意图

第2次交叉如图2所示:先分解染色体,得到工序的排序信息,然后根据Pa交叉段的数字的排序信息在Pc中找到对应的工序,将这些工序按照交叉段的工序排列顺序插入Pc中相应位置,形成最终交叉后的染色体Pd。因此,第2次交叉后变为Pd [22 11 13 31 12 23 33 33 21],并获得了交叉段的工序排序。

图2 第2次交叉示意图

3.4 变异算子设计

以一定概率随机交换染色体中基因的位置,重新排序,这个概率即为遗传算法的变异率。经过变异的粒子如果为可行解,则保留此交换,否则重新进行变异操作。

3.5 适应度函数与终止条件设计

本文的优化目标是使任务总完成时间最小,所以根据人员配置模型的优化目标函数确定优化算法的适应度函数为:

其中,x为一个可行解(即被选方案);fmin为遗传算法中每一代的f(x)的最小适应度值。

该算法如果达到给定的最大进化代数或者连续若干代群体的最优解的目标函数值变化不大时,便停止迭代。

4 实例验证

以某企业某一订单的人员配置为例,该订单包括3个工件,每个工件有3道工序,由3名操作工来完成,人员和任务之间的匹配度见表5所列,其中,工序后面括号里的数字为其所对应的任务量,单位是h。

表1 人员和任务之间的匹配度

采用上述遗传算法,借助Matlab7.0编写程序,设置如下优化参数[9]:初始种群为20,迭代次数为100,交叉率取0.8,变异率取0.15,计算结果如图3所示。

图3 人员调度甘特图

5 结束语

柔性生产过程中,由于人员技能的多样性和工序之间的次序约束关系,不同的人员调度方案直接影响任务的总完成时间。为了实现任务总完成时间最小的优化目标,本文根据操作人员对各任务的累计工作时间计算人员任务之间的匹配度,在此基础上建立柔性生产中人员调度数学模型;通过启发式算法得到模型的初始解,并运用改进的遗传算法对模型进行求解;最后通过具体实例验证了该求解模型的准确性与可行性。

[1] 高 丽,徐克林,朱 伟,等. 柔性生产中人员配置模型及其调度算法[J]. 哈尔滨工业大学学报, 2012, 44(5):144-148.

[2] 曹 乐,王 彪,刘 飞,等. 装配线多技能作业人员优化配置模型[J]. 重庆大学学报, 2010, 33(12):21-26.

[3] 孟志雷,叶春明,宁 凝. 单元制造系统的操作工分配方法[J]. 工业工程, 2009,12(1):84-87.

[4] 李英姿,张晓冬,张 硕,等.基于人员-任务-资源匹配度的产品设计项目静态调度[J].工业工程与管理,2012, 17(3):74-80.

[5] 刘明周,高 纳,葛茂根,等. 基于胜任指数的制造车间操作工优化配置模型[J]. 合肥工业大学学报:自然科学版, 2011, 34(10):1466-1469.

[6] 沈维蕾,黄 莉.基于组合赋权的装配线作业人员优化配置[J].合肥工业大学学报:自然科学版,2013,36(9):1034-1037.

[7] Kuo Y, Yang T. Optimization of mixed-skill multi-line operator allocation problem[J]. Computers & Industrial Engineering, 2007,53(3):386-393.

[8] 刘明周,张明伟,蒋增强,等.基于混合粒子群算法的多目标柔性Job-Shop调度方法[J].农业机械学报,2008, 39(5):122-127.

[9] 闫纪红,王子墨. 基于学习遗忘作用的人员调度实验设计及其软件开发[J]. 实验室研究与探索, 2011, 30(6):55-60.

(责任编辑 张淑艳)

Personnel scheduling of flexible job-shop problem based on person-task matching degree

ZHAO Ya-ling, GE Mao-gen, HU Jing, ZHANG Ming-xin, ZHANG Xi

(School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)

For single piece and small batch production of flexible job-shop problem, considering the diversity of operator skills and different skill levels for different tasks, the person-task matching degree is calculated according to accumulated working time of each operator on each task,and the mathematical model of personnel scheduling under resource constraint is constructed for flexible job-shop problem. The initial solution of the model is obtained by the heuristic algorithm, and the optimal personnel scheduling plan is obtained with the minimum duration by using the revised genetic algorithm to solve the model. Finally, the feasibility and accuracy of the model are verified by real cases.

flexible job-shop; personnel scheduling; genetic algorithm; matching degree; resource constraint

2014-01-22；

2014-03-28

合肥工业大学产学研校企合作资助项目(10-067)

赵亚玲(1989-),女,安徽合肥人, 合肥工业大学硕士生; 葛茂根(1979-),男,安徽安庆人,博士,合肥工业大学副教授.

10.3969/j.issn.1003-5060.2015.02.027

F273.1

A

1003-5060(2015)02-0270-04