例谈新课程下变式教学中的有效探究

摘 要：变式教学中的有效探究能促进学生的全面综合能力更上一层楼。依新课标理念，结合高三变式教学，从变式促进学生养成探究的学习方式，从变式促进学生形成探究的学习品质，从变式激发学生的探究学习。

关键词：新课程；变式教学；有效探究

众所周知，变式教学能促进学生探究能力的发展，但能真正实现学生有效探究的变式教学并没有多少，究其原因是大部分的变式教学课堂已经沦为教师表演智者的舞台、学生旁观解题的战场。因此，在新课标下实现有效探究的关键是教师应转变为学生的引路人，学习的路还是要学生自己走。教师要树立学生是课堂主体的意识，要提供合适的课题、创造和谐的氛围、设置合理的路标来激发学生的学习热情，真正放手让学生大胆地去探究，把课堂化为学生合作探究学习的天地，这样才能实现有效探究。以下笔者结合自己高三变式教学的实践，谈谈在教师引导下如何利用变式让学生通过探究活动将已学的知识、方法、能力进一步升级，从而多层次、多角度、多方面提高学生的综合数学素养。

一、源于变式方向的有效探究

变式教学通常是以一道典型题为范本进行衍化，而变式衍化的方向可以说是无穷的，一般情况下都是由教师备课时选择好某几个方向来展示给学生，然后在课堂上让学生品味，学生通常化身为教师的仰慕者，在课堂上激动地感受教师的神来一笔，而学生自身并不参与变式的产生过程，只是调动知识、思维参与变式后的解题与体会。这样的课堂显然不是学生进行有效的探究，而是展示教师的有效探究，因此变式教学中教师首先应将变式的衍化方向留给学生，让学生自己动手进行变式，教师仅需给予点拨即可。

例：（2014年辽宁卷理科第11题）当x∈[-2，1]时，不等式ax3-x2+4x+3≥0恒成立，则实数a的取值范围是（ ）

A.[-5，-3] B.[-6，-■] C.[-6，-2] D.[-4，-3]

教师选择此题作为范本，引导学生进行变式，教师唯一做的就是与学生一起分析题目的条件与结论，主要有以下五个方面：①x∈[-2，1]②ax3-x2+4x+3≥0③恒成立④实数a⑤取值范围。引导学生联系自己的学习情况，结合自己的解题经验，选择一个方向或几个方向设计一道属于自己的题目。这样学生的探究热情立刻高涨，积极主动地研究起来：有的学生去翻书，有的学生找笔记本，有的学生查试卷，也有的学生在沉思，还有的学生相互讨论。无论最后学生设计出的题目如何，这一刻学生正在做的就是实实在在的有效探究。有学生将②变为“ax3-x2+4x+3≤0”；也有学生将③变为“有解”；还有学生将①④同时变为“a∈[-2，1]，实数x”；当然还有学生添上一个条件，求定值；甚至还有的学生将结论与条件互换等等。

以上做法确实将“倡导积极主动、勇于探究的学习方式”落到了实处。在这种开放式的变式教学中，教师让学生打开思绪，从自身水平出发，不同的学生借助于不同的手段，探究一道没有定论的问题。在这个过程中学生要自己提出问题，自己进行设计，自己提取知识，进行切实可行的探究，并且明了探究是学习的一种方式，从根本上促进学生尝试、思考、选择、批判、肯定，实现自身的价值。这样的变式教学才能从本质上形成学生的有效探究。

二、基于变式过程的有效探究

当学生第一次设计了自己的变式时，那仅仅是探究的开始，此时学生的探究还只是停留在对题目知识的简单变化，大多数学生也只是单纯地从本源的知识上做基础性的变化，对同一章节内的知识进行了梳理与初探，还没能突破定式思维的束缚，探究不同章节与不同类型的知识方法的融合。此时教师就需要引导学生跳出框框，思考同一问题的不同表达形式，同一方法的不同表现形式，及时以范例来诱导学生，从而在变式教学过程中实现有效探究。

变式1：当x∈（0，+∞）時，不等式ax2-4ex+3≥0有解，求实数a的取值范围。

以上是学生的一道变式，教师在肯定其可行性后，就展示了下面变式给学生参考：

变式2：若角A是锐角，且满足2tanA=tan（A+B）tanB，求锐角B的取值范围。

此时学生一见到教师的范例立刻就有了耳目一新的感觉，这一股新的冲击波足以让学生更进一步思考变式的层次，跳出不等式到三角方程，从实数到角度，那还可以变得更远吗？还有其他更有意思的变式吗？学生又有了新的干劲，探索问题的范围扩展到所学习过的任何一类的知识方法。有的学生就得到以下变式：

变式3：已知O为坐标原点，设S是曲线C：y2=4x上不同于O的点，以OS为直径作圆与C相交另外一点R，求该圆的面积最小时点S的坐标。

显然，此学生能从教师的变式中体会到变式1与变式2在解题方法与解题模式相似，而题目的背景知识不同，即形散而神不散，并将变式推广应用到圆锥曲线，学生的表现让教师为之惊叹，学生为了更完美的变式，在知识的海洋中不断地探求不同知识方法的相似之处以及相同知识方法的区别与联系，于是乎，不时的有些许学生迸发出创造的思维火花。这样教师真正为学生开阔视野，成为数学探究的组织者、指导者，而循序渐进地、系统地培养学生的探究能力，不仅让学生养成了探究的习惯，而且让学生的探究水平大幅度提高。

三、趋于变式完美的有效探究

数学变式没有最好，只有更好；没有终点，只有起点。当学生能探究出自己的知识储备空间时，探究的脚步还不能够停下，因为有货物充足的知识仓库，还要有良好的物流后勤才能让市场活起来。当下学生的变式能类比推广到每个章节中，但还不能充分地将不同的章节知识进行融合、交汇、转化。只有让不同章节的知识要点在同一变式中达到你中有我，我中有你的境界，才能说明学生的探究品质得到终极升华。因此当下教师还要露一手画龙点睛之笔，让学生的探究无限逼近于完美之巅。

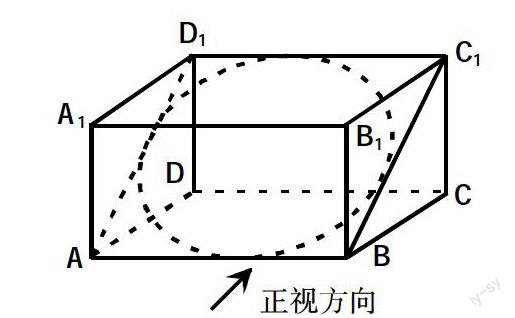
变式4：如下图，长方体ABCD-A1B1C1D1中AB=2，BC=a，CC1=b（a>b>0），截面四边形ABC1D1恰是圆O的外切四边形，则圆O的正视图是椭圆O′，求椭圆O′的离心率的取值范围。

此变式将立体几何知识与圆锥曲线问题有机地交融在一起，让等式隐藏在文字语言的叙述当中，需要发散思维的有效链接，只有学生找到转化间的桥梁，才能解决问题。当然这样的变式，学生很难能自己得出，教师给出此变式，意在创设一个让学生探究意犹未尽的情境，但有学生进一步得出下面一变式：

变式5：已知O为坐标原点，设S是曲线C：y2=4x上不同于O的点，以OS为直径作圆与C相交另外一点R，问是否存在使得OR，RS，OS为等差的圆，若存在，求出此时的点的坐标，若不存在，请说明理由。

学生能得到以上的变式，教师已感到非常高兴。因为这一变式充分地将数列的知识与圆锥曲线的知识进行融合，达到了教师预期的目标。这样的高度有的学生能达到，有的学生则无法达到，但这并不影响学生的热情，这样的互动变式教学让学生在不知不觉中走出了自己探究学习的天地，也让学生体会到知识是有生命的，它能随学生的学习与探究不断地发展、深化。

总而言之，在新课标的改革推进中，变式教学不能再是一言堂，要让学生成为变式教学的主人，教师只是学生的引路人。只有通过这样渐近性的变式互动探究，才能激活学生的大脑，促进学生学习能力的全面发展。数学教学的最根本目的不只是让学生学会数学知识与方法，更重要的是通过学习数学，体会与感悟学习的方法、手段、策略，从本质上提高学生的学习能力。而高三数学复习若能如此这般的常用变式，让学生去探究知识的完备、探究方法的应用、探究思维的破茧成蝶，那么学生习得的知识方法就能得到最大范围的自我检阅，学习方式与思维就能得到更好的锤炼，能力素养与理性精神也能得到升华。

参考文献：

[1]崔允漷.有效教学[M].上海：华东师范大学出版社，2009.

[2]陈旭远.新课程新理念[M].长春：东北师范大学出版社，2002.

作者简介：袁琴芳，女，中学高级教师，从事高中数学教学研究。

？誗编辑 张珍珍