带材拉矫过程中张力和弯曲对延伸率的影响程度分析

傅玉勇

(重庆赛迪冶炼装备系统集成工程技术研究中心有限公司 重庆401122)

带材拉矫过程中张力和弯曲对延伸率的影响程度分析

傅玉勇①

(重庆赛迪冶炼装备系统集成工程技术研究中心有限公司 重庆401122)

张力、弯曲半径(压下量)和延伸率是带材拉矫时的主要工艺参数，张力和弯曲的增加都有利于延伸率的增加，但张力和弯曲对延伸率的贡献率是有差异的。基于冷轧生产工艺参数，定量分析了两种材料模型的带材分别在最大张力和最大弯曲曲率条件下对延伸率的贡献率，结果表明弯曲对延伸率的贡献率最大可达77%～98%，最低也可达53%，而张力对延伸率的贡献率最大则为8%～47%，最低约为2%，由此说明，带材在拉矫过程中，弯曲对延伸率的影响起主要作用，而张力所起作用相对有限。

拉矫机 延伸率 张力 弯曲 贡献率

1 前言

拉矫机广泛应用于钢铁行业后处理机组中，是带钢板形改善的关键设备。张力、弯曲半径和延伸率是带材拉矫时的三个主要工艺参数，而带材所获延伸率大小与所受张力和弯曲半径密切相关，但张力和弯曲对延伸率的贡献率是有差异的。本文基于理想弹塑性材料和线性强化材料对带材在拉矫过程中张力和弯曲对延伸率的影响程度进行了分析和对比。

2 带材拉矫过程的力学分析[1][2]

2.1 分析假设

1)带材拉矫过程进行如下假设：

(1)平面假设；

(2)变形为平面应变状态；

(3)带材厚度方向的应力为0；

(4)拉伸过程中张力保持不变；

(5)材料为各向同性。

2)理想弹塑性材料和线性强化材料的应力应变曲线如图1所示。

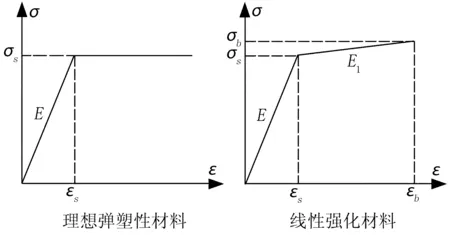
图1 应力应变曲线

2.2 理想弹塑性带材拉弯变形分析

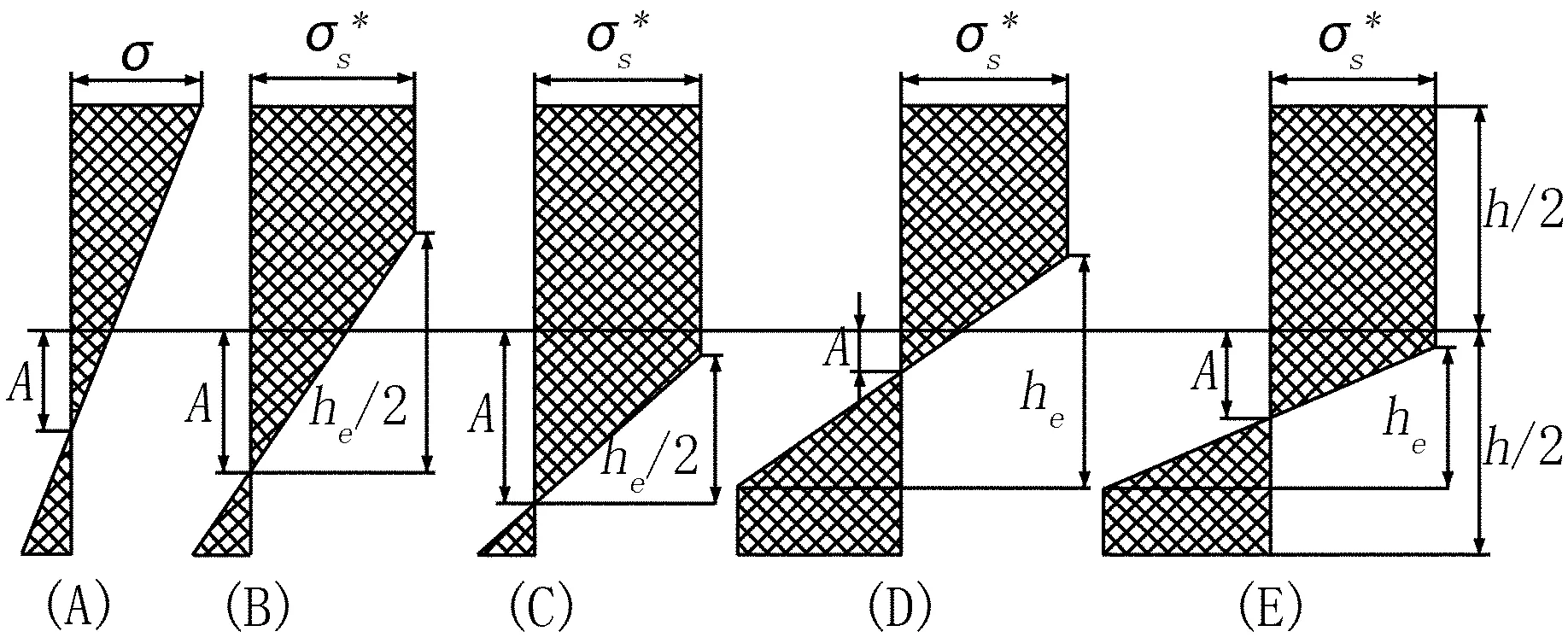
图2 拉矫时理想弹塑性带材的5种应力分布形式

如图2所示，拉矫时理想弹塑性带材可能出现的5种应力应变分布状态。在实际生产中，带材通过拉矫机弯曲辊时，通常处于(E)型应力分布状态[2]，即双侧弹塑性状态，则在单个弯曲辊上带材拉矫时中间层的变形—即延伸率εc可由下式表示：

(1)

中性层偏移量A为：

(2)

其中：

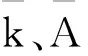
(3)

(4)

从(3)中可以看出，带材拉矫时，在其延伸率保持不变的情况下，张力与弯曲半径成正比关系，即张力增加时，弯曲半径必然增加，并且延伸率εc的大小与带材厚度h无关。

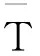
A—带材中性层相对几何中间层的绝对偏移量。

2.3 线性强化带材拉弯变形分析

同样，如图3所示，拉矫时线性强化带材可能出现的5种应力应变分布状态。同样在实际生产中，带材通过拉矫机弯曲辊时，通常也处于双侧弹塑性的(E)型应力分布状态[2]，则在单个弯曲辊上带材拉矫时中间层的延伸率可由下式表示：

(5)

同样，中性层偏移量A为：

(6)

其中：

式中 λ—强化系数； E1—强化模量。

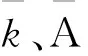
(7)

(8)

从(7)中可以看出，线性强化带材拉矫时，其延伸率保持不变的情况下，张力与弯曲半径近似成正比关系。

表达式(7)、(8)中其它数学符号的意义同前。

图3 拉矫时线性强化带材的5种应力分布形式

2.4 计算结果及分析

1)带材在拉矫过程中获得的延伸率是拉应力和弯曲应力联合作用的结果，它们对延伸率的影响不是简单的代数叠加，而是一个综合作用效果，要精确分析二者对延伸率的影响程度是困难的。现有的拉矫理论中[2][3]，分析带材通过一个弯曲

辊时，沿厚度方向的变形都假设为线性变化，因此采用线性分解的方式来近似分析张力和弯曲对延伸率的影响是可行的。在分析二者对延伸率的影响时，按如下思路进行：给定延伸率不变，再选定最小弯曲半径，根据材料特性和拉矫相关理论获得对应的最小张力，再根据张力计算值可得相应的拉应力和拉应变，由给定延伸率减去拉应变，即可获得弯曲所引起的最大变形，通过调整弯曲半径大小，使张力达到0.5σs，相应得到张力最大时的拉应变。

2)冷轧后处理机组中的拉矫机，一般为两弯一矫型，所处理带钢厚度大部分在0.35mm～2mm，延伸率一般选取0.3%～2%，本文分析时，按上述范围进行分析。拉矫时的单位张力一般按(0.2～0.5)σs选取，即张力系数为0.2～0.5，本文分析时最大张力按张力系数0.5选取；通常后处理机组中拉矫机工作辊径为φ30mm～φ40mm，本文选取R15mm作为最小弯曲半径进行计算。表1为线性强化带材和理想弹塑性材料机械性能参数。

3)根据表2的单辊延伸率计算值，并结合公式(3)、(4)、(7)和(8)分别对理想弹塑性材料和线性强化材料在拉矫时的张力和弯曲对延伸率的影响情况进行分析。本文在分析过程，略去了具体计算过程，仅给出相关计算结果。

表1 材料机械性能参数

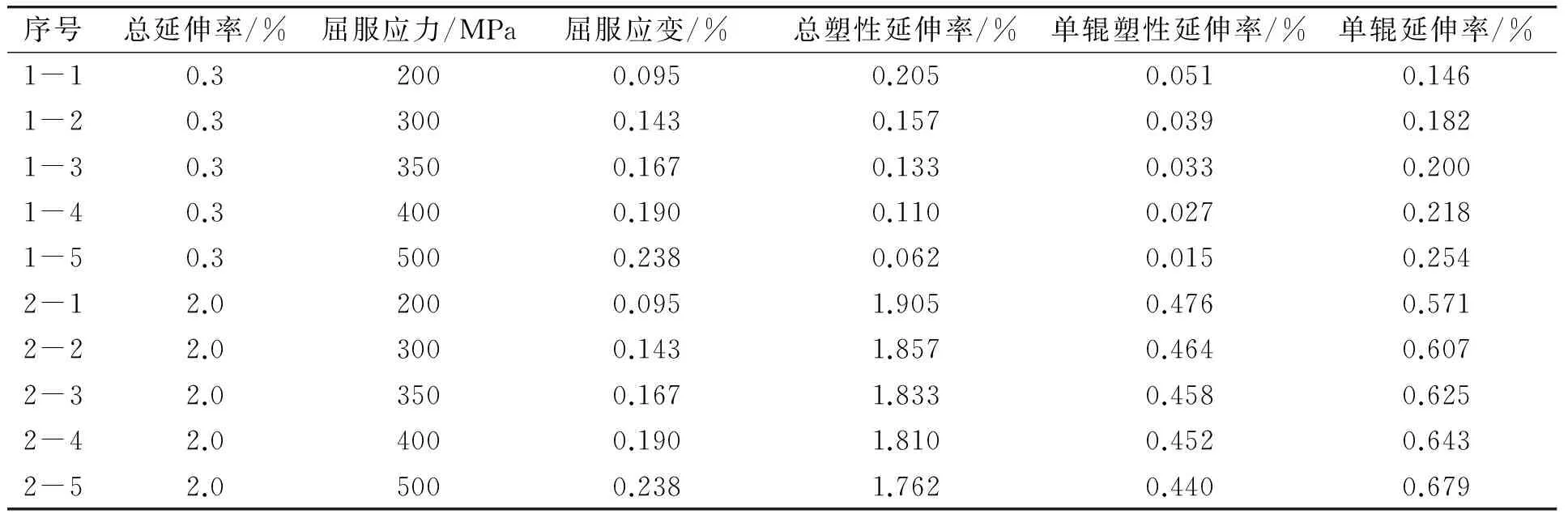
表2 单辊延伸率计算

表2为单个弯曲辊上的延伸率计算值。将总塑性延伸率均匀分配到到4个弯曲辊上，并加上弹性延伸率，从而得到单个弯曲辊上的延伸率。

4)表3为两种材料模型的计算结果，在最大张力系数为0.5条件下，当总延伸率为0.3%时，张力对延伸率的最大贡献率约为33%～47%,而总延伸率为2%时，张力的最大贡献率则约为8%～18%。从表3中可看出：

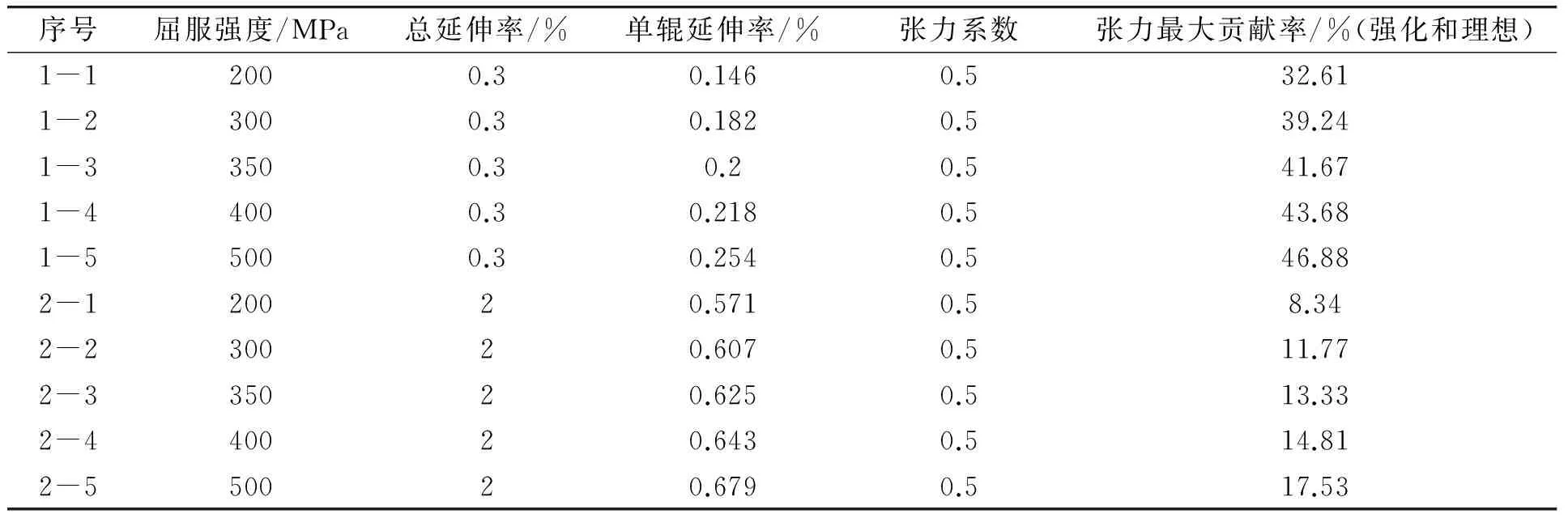
表3 最大张力时张力对延伸率的最大贡献率

(1)在保持延伸率不变的条件下，对于相同屈服强度的材料，无论是理想弹塑性还是线性强化材料，张力对延伸率的最大贡献率是一样的，此时对应的弯曲曲率最小，其对延伸率的贡献率也相应最小。

(2)随着带材屈服强度的增加，张力对延伸率的贡献率逐步增加，且与带材厚度无关。

(3)随着设定延伸率的增加，张力对延伸率的贡献率逐步减小。

5)表4为两种材料模型在最小弯曲半径R=15mm的条件下弯曲对延伸率的最大贡献率结果，低强度带材拉矫时，弯曲对延伸率的最大贡献率可达90%～98%，高强度带材则可达77%～96%。从表4可看出：

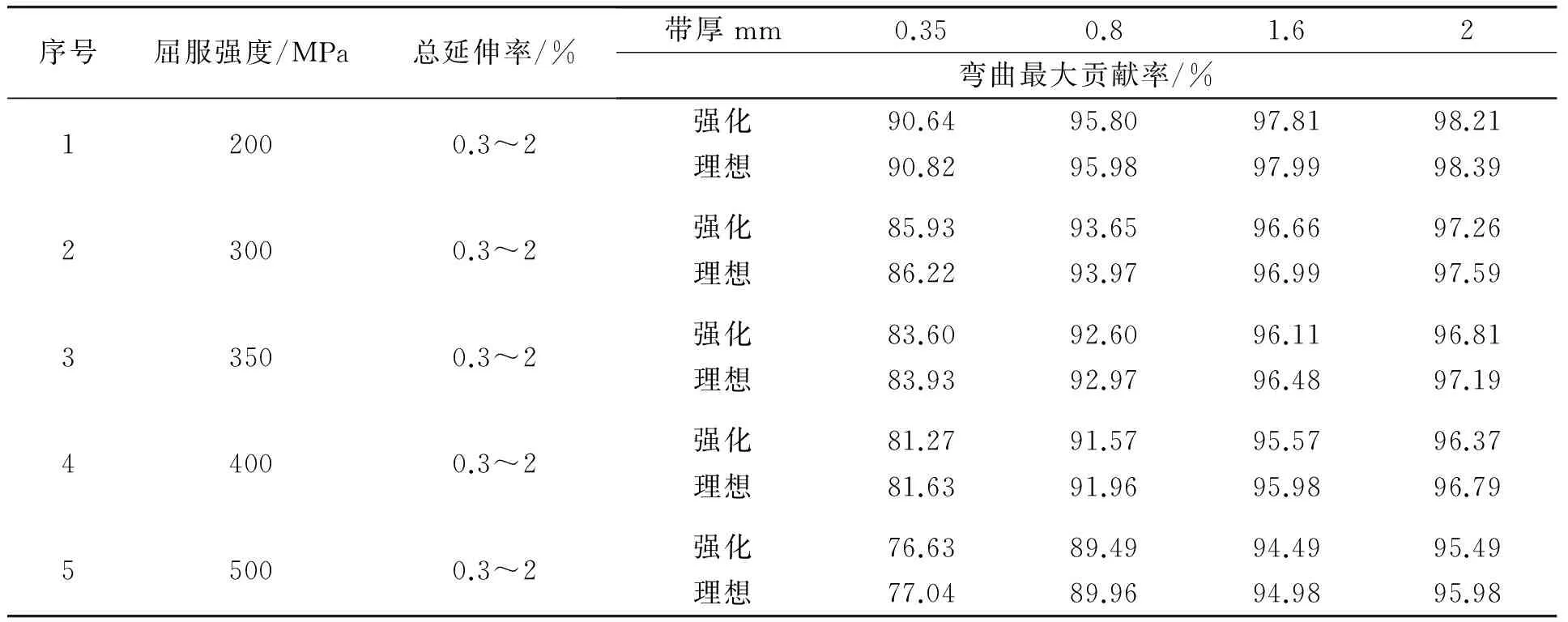
表4 最大弯曲曲率时弯曲对延伸率的最大贡献率

(1)对任意一种带材，无论对于线性强化带材还是理想弹塑性带材，在选定的延伸率范围内，弯曲对带材延伸率的贡献率是不变的，这是由于给定的弯曲半径都保持不变的缘故。

(2)两种材料模型在相同强度和厚度条件下，弯曲对带材延伸率的贡献率很接近，总体上，理想弹塑性带材略大于线性强化带材，这是由于线性强化带材获得相同的延伸率时，需要更大的拉力，因而拉伸的贡献率提高了。

(3)对任意一种带材，随着带材厚度的增加，弯曲对延伸率的贡献率会明显增加。

(4)随着材料屈服强度的增加，弯曲对延伸率的贡献率会逐步减小。

3 结语

根据冷轧后处理机组中的实际拉矫生产工艺参数，在极限条件下，基于两种材料模型，对拉矫过程中张力和弯曲对带材延伸率的影响程度进行了分析比较，计算结果表明：在极限条件下，弯曲对延伸率的贡献率最大可达77%～98%，最低也可达53%；同样，张力对延伸率的贡献率最大则为8%～47%，最低约为2%。由此说明，带材在拉矫过程中，弯曲对延伸率的影响起主要作用，而张力所起作用相对有限。因此，在生产中选择拉矫工艺参数时，在保证带材板形要求的情况下，尽量增大弯曲对延伸率的作用，这样可以减小施加在带材上的张力，从而降低对机组张力设备的能力要求，减少投资。

[1]肖林.弹塑性线性强化带钢的拉弯矫直过程分析.重型机械，1997(4):47～58.

[2]肖林.金属带材连续拉伸弯曲矫直变形机理研究.北京科技大学博士学位论文，1999.

[3]崔甫.矫直原理与矫直机械.北京:冶金工业出版社，2007.

Tension and Curvature Effect for Strip Specific Elongation During Stretcher-bender Levelling

Fu Yuyong

(CISDI R&D Co., Ltd, Chongqing 401122)

This paper introduces that the tension and the curvature are different effects on strip specific elongation during stretcher-bender leveling, and analyzes quantitatively the max efficiency of the tension and the curvature effects for the specific elongation. The result indicates the curvature his main effect on the specific elongation that maximum. efficiency can be 77%～98% and minimum value can be 53%, and the tension just has less effect on the elongation that max. efficiency is about 8%～47% and its min. value is about 2%.

Stretcher-bender leveller Specific elongation Tension Curvature Efficiency

傅玉勇，男，1975年出生，毕业于重庆大学机电工程专业，硕士，工程师，主要从事冶金设备设计

TG333.23

A

10.3969/j.issn.1001-1269.2015.01.003

2014-09-23)