应用极端原理解决与圆有关的中考最值问题

浙江省宁波市鄞州实验中学 蔡卫兵 (邮编：315100)

应用极端原理解决与圆有关的中考最值问题

浙江省宁波市鄞州实验中学 蔡卫兵 (邮编：315100)

中考压轴题中频繁出现有关最值问题，常让很多同学束手无策，望而生畏.其实与圆有关的中考最值问题大多由动点而产生，找出动点(相应动线)的极端位置，常常能确定最值.因为许多事物的性质和矛盾,最容易在其临界情况和极端状态下体现和暴露出来,所以在解决数学问题时,常常利用极端、临界的元素为"突破口",进行探索、推理论证,使"变动"转化为"确定",从而分散问题的难点使问题得到解决.2014年各地的中考试题有许多将圆的知识与最值问题综合起来考查，我们可以采取“谋定而后动”的策略，把问题引向极端，考察“特殊位置”、“特殊图形”，进而简化解题，提高解题速度.本文试图通过几道中考压轴题介绍极端性原理在解与圆有关的中考最值问题中的具体运用，供参考.

1 “连心线与圆的交点”为“到圆上动点距离之最值”的极端位置

例1 如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是______.

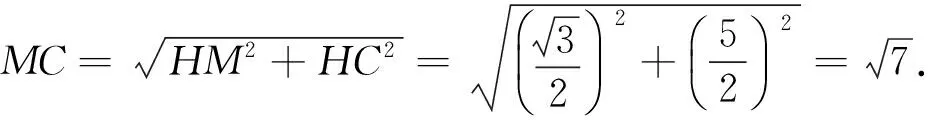
例2 在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在边DC，CB上移动．连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，若AD=2，试求出线段CP的最小值.

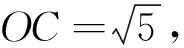
例3 如图∠BAC=60°，半径长1的⊙O与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的⊙P交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为______.

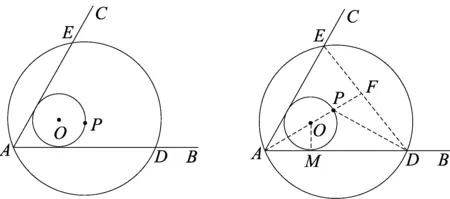
2 “弧的中点”为“圆上动点到定线距离之最值”的极端位置

例4 如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB=45°，则四边形MANB面积的最大值是______．

解析 过点O作OC⊥AB于C，交⊙O于D、E两点，连结OA、OB、DA、DB、EA、EB，如上图.

∵S四边形MANB=S△MAB+S△NAB，∴当M点到AB的距离最大，△MAB的面积最大；当N点到AB的距离最大时，△NAB的面积最大，即M点运动到D点，N点运动到E点，

例5 如图，已知在边长为8的正方形ABCD中，E是BC边的中点，P在过A、E、D三点的圆上，则△APE面积的最大值是______.

解析 设圆心为O，由垂径定理得，点P在AE的垂直平分线上时，点P到AE的距离最大，△APE面积的最大，过点E作EF⊥AD于F，连接AO.设圆的半径为r，

∵点E是BC的中点，∴BE=4，

在Rt△AOF中，AO2=AF2+OF2， 即r2=42+(8-r)2， 解得r=5.

3 “切线切点”为“有关角度之最值”的极端位置

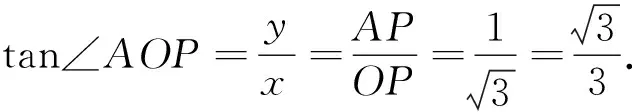
例7 我们规定：线段外一点和这条线段两个端点连线所构成的角叫做这个点对这条线段的视角.如图 ，在平面直角坐标系xOy中，已知点D(0，4)，E(0，1).点G为x轴正半轴上的一个动点，当点G对线段DE的视角∠DGE最大时，求点G的坐标.

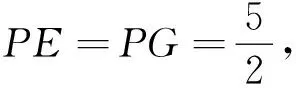
图1

图2 图3

(1)当⊙O的半径为1时，①在点D，E，F中，⊙O的关联点是______；

②过点F作直线交y轴正半轴于点G，使∠GFO=30°，若直线上的点P(m，n)是⊙O的关联点，求m的取值范围；

(2)若线段EF上的所有点都是某个圆的关联点，求这个圆的半径r的取值范围.

解析 (1) ①D、E；

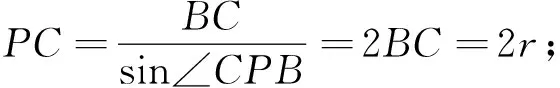
∴若P点为圆C的关联点；则需点P到圆心的距离d满足0≤d≤2r；

由上述证明可知，考虑临界位置的P点，如图2：点P到原点的距离OP=2×1=2；

易得点P1与点G重合，过P2作P2M⊥x轴于点M，易得∠P2OM=30°，

4 “直径为圆中最长弦”为“有关线段之最值”的极端情形

例9 如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH的最大值为______．

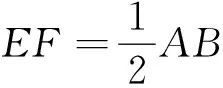
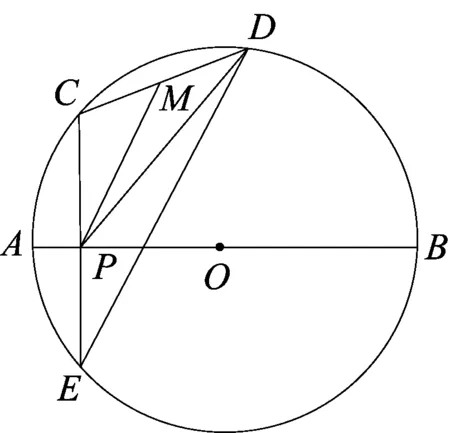
例10 如图，C、D是以AB为直径的⊙O上的两个动点(点C、D与点A、B不重合)，在运动过程中弦CD长始终保持不变，M是弦CD的中点，过点C作CP⊥AB于点P．若CD=3，AB=5，PM=l，则l的最大值是______．

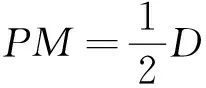
综上所述，解决圆有关的中考最值问题，若能灵活地利用常见的极端、临界的元素为“突破口”，便有简洁、明快的解题效果.

2015-03-25)