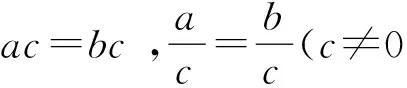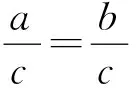还数学课堂一份宁静

江苏省海门市东洲国际学校 茅雅琳 (邮编：226100)

还数学课堂一份宁静

江苏省海门市东洲国际学校 茅雅琳 (邮编：226100)

1 问题起因

学校组织了青年教师优课评比，作为评委，我听了他们精心准备的参赛课，课题是《9.1.2不等式的性质》(人教版)，由于都是工作五年内的青年教师，课堂有些缺陷是难免的.但是，其中有一个共同的现象，却引发了我的思考，这五位教师不约而同都采用了小组合作学习的形式，课堂显得热闹非凡.走近孩子们倾听，发现热闹的表面透出的不全是思维的活跃，还有不该有的浮躁与肤浅，众声喧哗中充斥的甚至是互不相干的自言自语，这样的表面热闹中错过了该有的意义的生成.

日本著名教育专家佐藤学先生在《静悄悄的革命》一书中说道：“应当追求的不是‘发言热闹的教室’，而是‘用心地相互倾听的教室’.”“在教室里的交流中，倾听远比发言更重要.”结合本人近20年的数学教学感悟，竟然开始怀念原有的数学课堂氛围，觉得有必要呼吁，还数学课堂一份宁静.

2 问题症结

反思现今数学课堂这种不协调氛围起因，主要有以下几点：

2.1 曲解了新课程理念

《全日制义务教育数学课程标准(实验稿)》的基本理念是关注学生的发展.《标准》特别提出，要使学生获得对数学理解的同时，在思维能力、情感态度与价值观等多方面得到进步和发展.“把课堂还给学生，让课堂充满生命活力”.叶澜教授早在1997年就提出这样对生命的呼唤，数学课堂学习的生命在哪里？在肤浅的师生问答？在形式的合作交流？在浮躁的课堂氛围？不，数学学习的生命在于数学的思维.

2.2 变相的灌输式教学

虽然是年轻教师，但是由于他们在受教育时期，接受的是陈旧的教学方式，在他们踏入课堂的时候，自然就沿用了自己所接受过的教学方式，这些表面的热闹氛围，其实质是在原有教学方式的基础上，披上了一层华丽的外衣，其本质，仍是没有真正以学生为主，没有真正关注学生的发展.否则，怎会无视学生的参与？怎么会无视学生的思维？怎会无视学生的情感？

2.3 缺乏对教材的二次开发

教材从天平出发，得出不等式的三个性质.五位教师采用的都是预先在黑板上给出教材中提到的几组具体数据，让学生通过交流得出三个性质.结果学生都能顺利地发现不等式的三个性质.学生对不等式的性质真的了解了吗？课后的作业显示，学生对第三个性质的应用差错很多，究其原因，就是因为课堂上没有给他宁静的氛围，提供足够的时间和空间，让学生进行必要的思维，学生只是知其然而不知其所以然.其实教师为什么举了这样特殊的数据让学生分析？举这样数据的依据是什么？换成另外的一些数据行不行？这些问题都应是学生主动探究过程中需要思考的问题，而这样的思考才是最有价值的.

3 教学建议

教之道在于“度”，学之道在于“悟”.数学学习更是如此.我们要让学生找到研究新知的思路，掌握分析问题的策略，探寻解决问题的途径.现代数学教育理论认为：“数学是思维活动的过程，数学教学是数学思维活动的教学.”教师传递的只是信息，知识必须通过学生的主动建构才能获得.也就是说学习是学习者自己的事情，谁也不能代替.如关于不等式性质的得出，不需要所谓的讨论、交流，学生需要的就是一个宁静的思维氛围.

3.1 类比引发思维

师引：我们前面学习了等式的基本性质，关于不等式，它会有怎样的性质呢？

生思：和等式性质类似，应该也有关于加减和乘除的两个性质.

这样的类比，在学生的学习经历中，会遇到多次.如线段的垂直平分线与角平分线的性质类比学习，不等式与方程类比学习，方程组与方程类比学习，二次方程和一次方程类比学习，二次函数与二次方程类比学习，四边形与三角形类比学习等，在学生的后续自主学习中，更是一种很好的数学思想.

3.2 猜想启迪思维

师启：请同学们用类比的思想猜想不等式的性质.

生思：类比等式性质1，如果a=b，那么a+c=b+c，a-c=b-c，猜想不等式的性质1，如果a>b，那么a+c>b+c，a-c>b-c； 如果a

这样的类比猜想是合情猜想，虽然大家知道不等式的性质和等式的性质并不完全一样，当不等式的两边乘除同一个负数时，不等号的方向需要改变，但是这是本节内容的重点和难点，学生目前的类比只是一种知识的迁移，猜想只是一种知识的拓展.这种类比猜想在数学解题中，对学生的思维有很好的指向性作用.如中考题变式问题中，图形进行一定的变换后，问原有结论是否成立，并进行证明.大多数都是用这种类比猜想解决.数学学习很重要的一点就是培养学生的分析能力，寻找解题的思路，这里的类比猜想就能给学生以很好的解法启示.

3.3 验证激发思维

师激：请尝试说明你的猜想.

生思1：以上的结论是类比等式性质得到的，我的猜想正确吗？

这里猜想的依据是类比，但毕竟已知的是等式的性质，并非不等式的性质，对猜想持怀疑态度是一种理性的思维，数学学习讲究的就是步步有据.

生思2：怎样说明我的猜想是正确的呢？先举几个具体的数据验证一下.

这是很好的一种探究新知的途径，先猜想再用特殊值验证.这里特殊值的取法不同学生之间会存在差异，不同性格的学生展示不同的取值方法.有的学生比较浮躁，他会只取了几个正整数就轻易得出结论，还有的学生比较细心，为了让自己的结论更具有说服力，他举了分数、负数，进而发现不等式的性质2有该改进的地方.

3.4 碰撞完善思维

建构主义学习理论认为：学生的学习是一种主动建构的过程，只有学生主动建构，调整自己的心理认知结构或改造外部的知识结构，使得主客观彼此一致，才能建立新的认知结构.对同一个数学内容的学习而言，不同的个体也完全可能由于生活背景和个体经验的差异有不同的思维过程.数学教学要求学生独立思考，鼓励学生创造性的思考，让学生把思考的过程，结果有条理地说出来，这有利于培养学生的思维能力，拓展学生的思维空间.

师：请同学们互相交流自己的验证过程，完善自己的猜想.

这时的课堂展示的是一个热闹非凡的课堂氛围，这是真正的思维碰撞，这时的热闹是发自内心的对知识的渴求.

没有思维的数学学习不是真正意义上的学习，没有一定思维深度的数学学习不是好的数学学习.数学课堂展示的应该是一种丰富的千姿百态的安静，但学生内在的思维活动则犹如翻江倒海般汹涌.让我们创设一个宁静的数学课堂，让学生在宁静的气氛中驰骋想象，使学生的个性思维得到充分发展.

1 章建跃.中学数学课改的十个论题(续)[J].中学数学教学参考，2010(4)中旬

2 冯卫东.教育有必要从倾听开始[J]. 江苏教育，2010(2)(教育管理)

3 李建军.教学倾听：与儿童实现“视界融合”[J].江苏教育，2010(2)(教育管理)

4 徐菊芳.建构主义学习理论指导下的数学概念教学案例研究[J].中学数学教学参考，2010(4)中旬

2014-12-17)