围绕知识本质 加强能力考查——安徽近几年高考数学试题特点之我见

安徽师范大学数计学院 安徽省和县第一中学 徐祝云 (邮编：636150)

复习考试

围绕知识本质 加强能力考查
——安徽近几年高考数学试题特点之我见

安徽师范大学数计学院 安徽省和县第一中学 徐祝云 (邮编：636150)

历时九年，安徽省高考数学自主命题已经日臻成熟．试题在逻辑性、探究性和应用性等方面进行了不断的创新，所命制的试题注重考查知识的本质，力求多层次、多角度考查考生的数学能力和数学素养．近几年的安徽数学试卷在保持难度平稳的同时，更加突出能力考查的意识，下面结合具体的试题，探讨安徽卷在数学能力考查方面的几个落脚点.

1 从解决实际生产和社会生活中的问题出发

学习数学的最终目的是要把所学知识运用到日常生活中，从源头来寻找考查点也是充分体现我们教育的本质．这类试题背景比较贴近学生的生活，根据实际问题自然而然引出数学模型，并对其分析、求解．例如：

例1 (2012年理科第10题)6位同学在毕业聚会活动中进行纪念品的交换, 任意两位同学之间最多交换一次, 进行交换的两位同学互赠一份纪念品. 已知6位同学之间进行了13次交换, 则收到4份纪念品的同学人数为

(A)1或3 (B)1或4 (C)2或3 (D)2或4

该题具有一定的现实意义，与学生的实际生活有直接的联系，从而使学生易于感受数学的应用价值，考查了考生建模能力.用图示方法分析各种可能的情况，是一种重要的解决数学问题的策略和方法.

例2 (2013年理科第21题)某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动，分别由李老师和张老师负责．已知该系共有n位学生，每次活动均需该系k位学生参加(n和k都是固定的正整数)．假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系k位学生，且所发信息都能收到．记该系收到李老师或张老师所发活动通知信息的学生人数为X．

(I)求该系学生甲收到李老师或张老师所发活动通知信息的概率；

(II)求使P(X=m)取得最大值的整数m．

该题以考生熟悉的“心理测试活动”、“信息通知的发送”为背景而设计的，主要考查古典概型，计数原理，分类讨论思想等基础知识和基本技能，考查抽象概括能力，逻辑推理能力，运算求解能力，以及运用数学知识分析和解决实际问题的能力．解答第(II)问，可根据乘法计数原理，用组合数表示事件{X=m}所含基本事件的个数并求出P(X=m)，将问题转化为求不等式P(X=m)≤P(X=m+1)的解．给优秀学生提供了展示创新思维的平台.

2 利用陈题作为素材，重新构造新情境

陈题新作，不是仅仅在条件或结论中寻求一点点变化，而是抓住问题的实质，重新构造全新背景，不留一点痕迹，确保公平性．例如：

3 关注知识点的交汇处，拓宽交汇视野

注重学科的内在联系和知识的综合性，从学科的整体高度和思维价值高度考虑问题，在知识网络的交汇处设计试题，使对数学知识的考查达到必要的深度．例如：

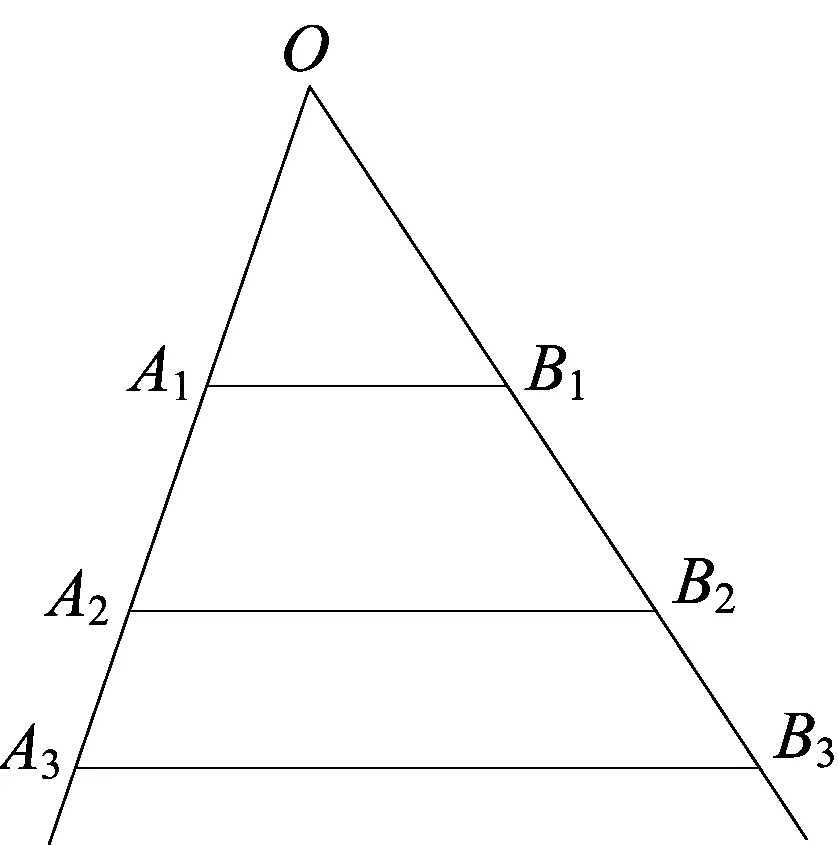
该题构思独特，巧妙地把平面几何知识与数列结合起来，原创性较强，考查学生利用所学知识解决问题的能力．试题有多种解法，考查学生优化解题的能力．

4 合理构造新概念，注重与高等数学衔接

这种类型的试题并没有将高等数学的概念直接拿来用，而是从高中数学基础出发重新定义，使考生易于理解，主要是考查其应用能力．例如：

例5 (2011年理科第15题)在平面直角坐标系中，如果x与y都是整数，就称点(x,y)为整点，下列命题正确的是______(写出所有正确命题的编号).

①存在这样的直线，既不与坐标轴平行又不经过任何整点

②如果k与b都是无理数，则直线y=kx+b不经过任何整点

③直线l经过无穷多个整点，当且仅当l经过两个不同的整点

④直线y=kx+b经过无穷多个整点的充分必要条件是：k与b都是有理数

⑤存在恰经过一个整点的直线

本题是多选填空和信息给予题的有机结合，使试题的新颖性与创造性大为增强，对相应的数学知识、数学方法的考查也更加全面深入，通过定义“整点”这一新概念，设置新颖的数学情境，要求考生能够形成知识和能力的有效迁移．试题设置有较高的综合度，要求考生有较强的思辨能力，着重考查考生理性思维的深度与广度．

5 利用多选填空设计，全面考查多重数学能力

安徽自主数学命题从2006年开始每年都设置了多选填空题，该种试题信息量大，考查考生的综合推理能力，有效地降低随机猜测的可能性，加强了试题的新颖性、探究性与创造性，对提高整卷的区分度起到很好的作用．例如：

例6 (2012年文科第15题)若四面体ABCD的三组对棱分别相等，即AB=CD，AC=BD，AD=BC，则下列命题正确的是______(写出所有正确命题的编号)．

① 四面体ABCD每组对棱相互垂直

② 四面体ABCD每个面的面积相等

③ 从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°

④ 连接四面体ABCD每组对棱中点的线段相互垂直平分

⑤ 从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长

本题取材于一个较为常见的四面体，三组对棱分别相等的四面体为一类特殊的四面体，这一类四面体具有自身独特的性质.这些性质的推导、论证可体现学生综合运用几何知识解决问题的能力，较好的体现了多选填空题这种题型的考查功能.

例7 (2013年理科第15题)如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A、P、Q的平面截该正方体所得的截面记为S．则下列命题正确的是____(写出所有正确命题的编号)．

本题以正方体为背景，考查正方体与平面的位置关系、空间线段长度、平面图形面积的计算，通过平面与正方体截面的动态变化考查空间想象能力和运算求解能力，构思新颖，内涵丰富．解答起来一气呵成，耐人寻味.

总之，安徽高考数学试题非常注重问题情境的设计，构造有一定深度和广度的数学问题，在试题的背景、形式、内容甚至解答方法等方面下功夫，使试题具有一定的新颖性和独特性，考查学生的创新意识和创新能力，对中学数学的教学有积极的导向作用，同时也利于高校人才的选拔．

2015-03-03)