挖掘一道“华约”自主招生题的含义
2015-06-15江苏省盐城市教育局教科院邮编224000
江苏省盐城市教育局教科院 吴 彤 (邮编:224000)
挖掘一道“华约”自主招生题的含义
江苏省盐城市教育局教科院 吴 彤 (邮编:224000)
1 试题呈现
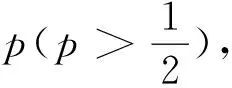
该试题取材于高中生都熟悉的“五局三胜制”,然而它不落俗套,提出了概率差的函数问题,具有较强的实际意义,本文将结合这道试题的解答与结论,力求透视出试题所隐含的深层意义.2 解题与反思
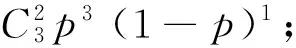
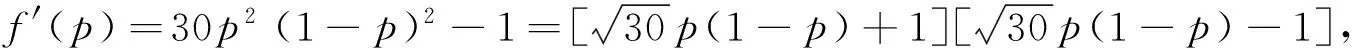
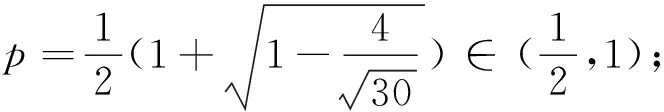
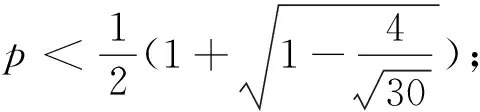
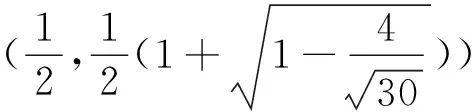
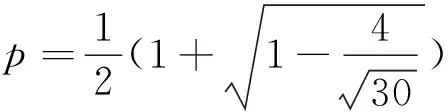

3 归纳与猜想
为了便于叙述,我们把采用只比赛一局、三局两胜制、五局三胜制、…、甲获胜的概率依次记为f1(p)、f3(p)、f5(p)、…、f2n-1(p)(n∈N*),容易得到:
……
∴f3(p)-f1(p)=3p2-2p3-p=2p2-2p3+p2-p=p(1-p)(2p-1),
∴f5(p)-f3(p)=6p5-15p4+12p3-3p2=3p2(2p3-2p2-3p2+3p+p-1)
=3p2(1-p)2(2p-1),
归纳猜想 甲、乙两人进行一场比赛,已知甲赢一局的概率为p,如果采用只比赛一局、三局两胜制、五局三胜制、…、甲获胜的概率依次记为f1(p)、f3(p)、f5(p)、…、f2n-1(p)(n∈N*). 那么
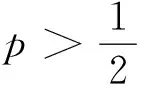
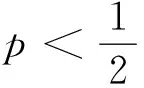
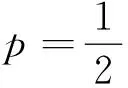
4 猜想的论证
该猜想就是要证明f2n-1(p)(n∈N*)的单调性,因而只要能求出f2n+1(p)-f2n-1(p)的正负即完成证明,根据上文有:
注意到p与1-p的指数关系,笔者思考的是,不急于直接化简f2n+1(p)-f2n-1(p),而是先求f2n+1(p)-pf2n-1(p),则
即f2n+1(p)-pf2n-1(p)

于是f2n+1(p)-pf2n-1(p)

所以f2n+1(p)-pf2n-1(p)
即p[f2n+1(p)-f2n-1(p)]
该结论说明甲、乙两人进行比赛,如果只比赛一局,甲赢的概率大(小),那么增加比赛的局数,甲赢的概率会更大(小)
2015-04-08)
