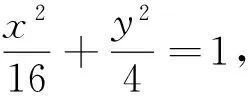抓住联系 突破思维障碍 实现有效转化——一道模考题赏析与思考

中国科学技术大学附中 黄严生 (邮编：230051)

合肥师范学院数学与统计学院 李 茜 (邮编：230601)

教学参考

抓住联系 突破思维障碍 实现有效转化
——一道模考题赏析与思考

中国科学技术大学附中 黄严生 (邮编：230051)

合肥师范学院数学与统计学院 李 茜 (邮编：230601)

函数是高中数学主干知识，也是高考中重点考查的知识.利用导数研究函数的性质和不等关系，不但是历年高考重点考查内容，而且常常在高考中作为压轴题.今年合肥市高三第一次质量检测数学试题，第20题是利用导数研究函数单调性和证明不等式问题，笔者对此题做了深入的分析研究，并形成了以下的认识、思考，供各位同仁参考.

1 试题呈现与解析

设函数f(x)=x3-3ax2+3(2-a)x，a∈R，

(Ⅰ) 求f(x)的单调递增区间；

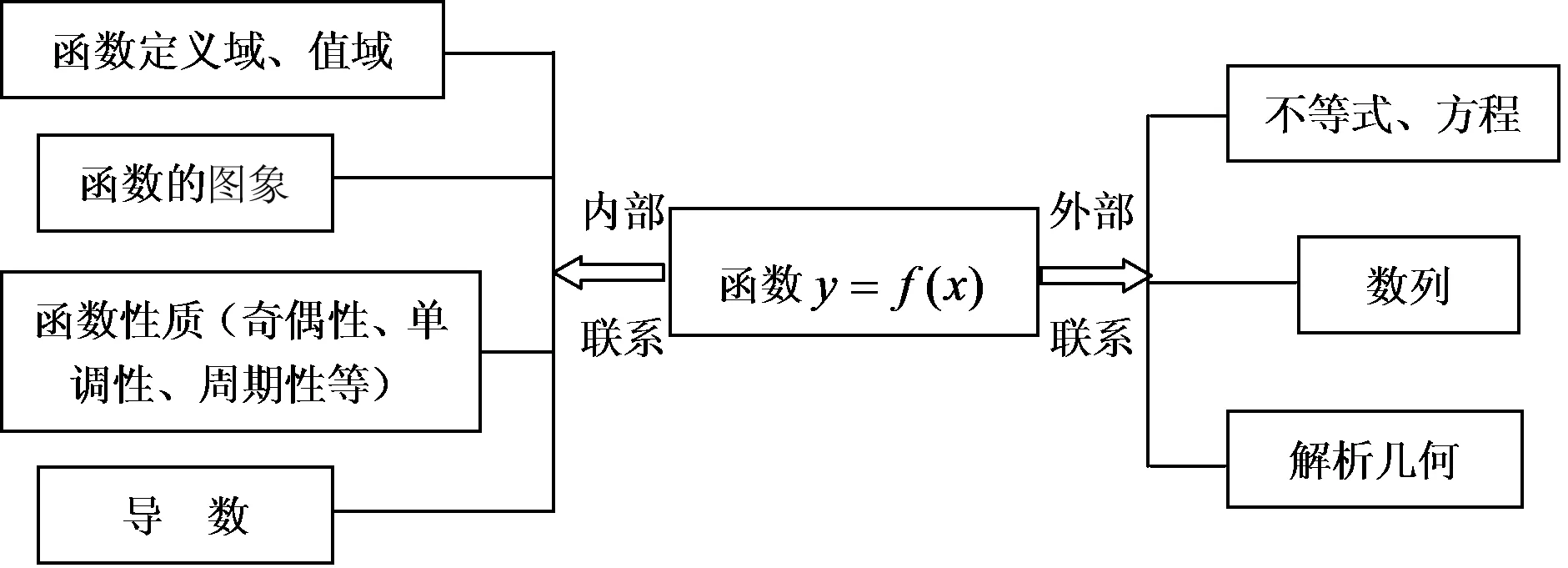
(Ⅱ) 若y=f(x)的图象与x轴相切于原点，当0

求证：x1+x2<8．

解 (Ⅰ)f′(x)=3x2-6ax+3(2-a)，

△=36(a2+a-2)=36(a+2)(a-1)，

f(x)的单调递增区间为(-);

(ⅱ)当-2≤a≤1时，f(x)的单调递增区间为(-,+)．

(Ⅱ)f′(x)=3x2-6ax+3(2-a)，由f′(0)=0，得a=2.

f(x)=x3-6x2，f(0)=0，由(Ⅰ)知f(x)的在(-,0)，(4,+)上单调增，在(0,4)上单调减，所以a=2符合题设.

∵f(x1)=f(x2)，0

∴04，

则8-x2>4，而f(x2)-f(8-x2)=(2x2-8)(x2-4)2<0，

所以f(x2)

f(x)在(4,+)上单调增，故x1<8-x2，即x1+x2<8.

2 试题剖析

本题以三次多项式函数f(x)=x3-3ax2+3(2-a)x(a∈R)为载体，第一问是利用导数研究函数的单调性，研究函数的单调性其实质就是研究导函数的零点.由于函数f(x)导函数是含有参数的二次函数，所以，转化为讨论二次函数的零点，也就是研究二次方程的根存在性问题.从而，就参数a进行讨论，即解不等式f′(x)=3x2-6ax+3(2-a)≥0和f′(x)=3x2-6ax+3(2-a)<0，求得相应的单调区间.

第二问进一步给出曲线y=f(x)与x轴相切于原点，其目的是求出参数a的值. 如何将曲线这一几何特征，转化为代数特征，是解决问题的关键.数学问题给出方式有两种形式，一是代数表征，一是几何表征.代数表征包括文字表征和符号表征，几何表征有直接用图形表征和文字表述的形式说明几何表征. 曲线与x轴相切于原点的代数表征是f′(0)=0,f(0)=0，进而求出参数a的值.在由条件0

此题考查了函数、导数、不等式等数学知识，利用导数研究函数的单调性，利用导数研究不等关系，对导数的考查比较深刻.重点考查了数形结合、函数方程、分类整合、转化与化归等数学思想方法.突出考查了学生分析问题、解决问题能力和创新能力.试题这样设计，符合新课程标准的要求，既贴近高中数学教学和教材，又符合高考要求.课程标准明确指出，了解函数在某点取得极值的必要条件和充分条件，会用导数求不超过三次多项式函数的极大值、极小值，以及闭区间上不超过三次的多项式函数的最大值、最小值；体会导数方法在研究函数性质的一般性和有效性.新课标中还指出，在教学中应注意沟通各部分内容之间的联系，通过类比、联想、知识迁移和应用等方式，使学生体会知识间的有机联系，感受数学的整体性，进一步理解数学的本质，提高解决问题能力.

3 联想与拓展

数学是联系的，数学知识间的相互联系，如函数与不等式、函数与方程、数列与函数、解析几何与函数、解析几何与平面几何等等.对于一道数学题来说，与之联系问题有很多，往往这种联系没有被发现，或者被发掘出来，尤其是一些数学素养不高的学生，是不能发现这种联系的.一般总是孤立地看问题，也就不能将知识融会贯通，因此，这些学生做一道题，只是做了这道数学题，不能触类旁通，举一反三，只是量的积累，不能提升其思维能力和分析问题、解决问题能力.我们经常听到学生说，我做了很多题，还不能提高自己的成绩.家长说我的孩子学习很刻苦，每天学习到深夜，做了很多的数学题，数学成绩总是不理想等等.因此，教师的教学，应积极引导学生用联系的观点看问题，学会洞察知识间的关系，发现数学问题之间相互联系.下面是笔者通过对本题研究产生的感悟和联想.

联想1 若函数f(x)是偶函数，且在区间(-,0]上单调，且f(x1)=f(x2)(x1≠x2)，则x1+x2=0.

我们知道函数f(x)是偶函数，f(x1)=f(x2)(x1≠x2)，不妨设x1

联想2 函数y=f(x)的图象关于直线x=a对称，f(x1)=f(x2)(x1≠x2)，且f(x)在(-,a]上单调，则x1+x2=2a.

由于函数y=f(x)的图象关于直线x=a对称，f(x1)=f(x2)(x1≠x2)，不妨设x1

联想1和联想2中函数图象分别关于直线x=0和x=a对称，而且分别在(-,0]和(-,a]上单调，分别在[0,+)和[a,+)也单调，不但在对称区间上单调性相反，而且增长速度和衰减速度相同，即对称点处的导数的绝对值相等.联想1和联想2中x=0和x=a也是函数的极值点，函数图象关于极值点对称.若函数图象在极值点两侧不成对称图形，也就说在极值点两侧增长(衰减)的速度不同，问题又会怎样呢？从而得到以下的拓展.

拓展 若将上面命题进行拓展，函数f(x)在x=a处取得极值，且函数f(x)在(-,a)单调增(减)，函数f(x)在(a,+)减(增)，若f(x1)=f(x2)，不妨设x1a，2a-x1>a，于是通过计算，判断f(2a-x1)-f(x1)值的符号，即f(2a-x1)-f(x2)=f(2a-x1)-f(x1)>0(或<0)，从而f(2a-x1)>f(x2)(或f(2a-x1)2a).

一般地，函数f(x)在x=a处取得极值，且函数f(x)在(-,a)单调增(减)，函数f(x)在(a,+)减(增)，若f(x1)=f(x2)，f(2a-x2)>f(x2)=f(x1)(或f(2a-x2)2a).

数学不是孤立的，数学问题之间是相互联系的，这种联系实质上揭示了数学的本质属性，只要抓住了，就能发现问题的本质，就能举一反三，就能创造性的提出解决问题的方法.

4 几点教学建议

4.1 注重知识梳理，发展学生的整体性思维和系统性思维

知识结构包含两个基本要素：一是最基本的知识；二是其它知识与最基本知识的联系.所谓掌握知识结构，实质上就是掌握这两个基本要素.真正的结构是以思维为基础的，而思维是以追问事物之间的本质性联系为本质特征. 数学理解就是指学生在已有数学知识和经验的基础上，建立新知识的个人心理表征，并不断完善和发展头脑中的数学知识网络，同时能将纳入知识网络中的新知识灵活地加以提取和应用.

从上表可以看出，函数中要素是自变量和因变量y，要素之间的联系是对应关系，通过对自变量x取值的研究，函数值y的变化规律，从形成函数性质.如奇偶性、单调性、周期性，函数的值域等等，这些函数内部的联系.而外部联系利用函数性质的研究不等式和方程的根问题，研究直线与曲线位置关系问题，特别曲线的切线问题.为此，就有了更新函数知识系统的需要，就有了学习导数需要，利用导数的几何意义解决函数的切线问题.而导数的引入，又为研究函数的单调性提供了一种工具.新知识导数的学习，不但使已有的知识系统得到丰富和扩充，而且使已有的函数知识系统赋予了新的意义.

4.2 强化转化意识，提升学生思维品质

数学思想是对数学知识的本质认识，是对数学规律的理性认识，是对某些具体的数学内容和对数学的认识过程中提炼上升的数学观点.它在认识活动中被反复运用，具有普遍的指导意义.从数学的角度提出问题、解决问题的过程中所采用的各种方式、手段、途径等就是常说的数学方法.数学解题的过程，就是将未知的数学问题转化已经解决的问题，或者与已解决问题相类似的问题的过程，这就是我们通常所说的化归.化归的目的就是达到化难为易，化复杂为简单，化隐含为明了，化陌生为熟悉.实际上是通过转化，将问题的题设与目标之间，隐含的数学概念、法则、公式、定理、公理、性质等明晰地梳理出来，根据其因果关系，将这些数学概念、法则、公式、定理、公理、性质等有序的排列出来，并用数学符号和文字表征出来.这一过程实际上就是破译解题密码的过程，只有有效地破译解题密码，才能创造性地提出解决问题方法，学生的数学思维能力才得以提升.

4.3 强化问题意识，培养学生提问题的能力

思维由问题开始，问题是思维的起点，又是思维的动力，好的问题能引起学生学习兴趣，激发学生火热的思考.美国教育家鲁巴克认为：“最精湛的教学艺术，遵守的最高准则，就是学生自己提出问题.”爱因斯坦：“提出一个问题往往比解决一个问题更重要，因为解决一个问题也许只是一个数学上或实验上的技巧问题.而提出新的问题、新的可能性，从新的角度看旧问题，却需要创造性的想象力，而且标志着科学的真正的进步”.如在研究直线与平面平行的性质时(a，b是两条不重合直线，α，β两个不重合的平面)，我们把这平面和直线作为研究对象，以它们之间是否形成确定的关系为切入点，通过思考、作图、观察、类比、联想、猜想等，发现众多命题.以“a//α为大前提”，就可以提出下面的命题来研究：

(1)若b//a，则b//α;

(2)若b//α，则b//a;

(3)若b⊥a，则b⊥α;

(4)若b⊥α，则b⊥a;

(5)若β//a，则α//β;

(6)若α//β，则β//a;

(7)若β⊥a，则β⊥α;

(8)若β⊥α，则β⊥a.

以上的命题有的是真命题，有的是假命题，有的有意义，有的没有什么实质意义，可以使学生从中感悟提问题的切入点和策略，以及思维方向和路径，对培养学生提问题能力大有裨益.正如著名数学家教育家波利亚所说“问题是数学的心脏”，所以，要积极倡导问题教学.所谓问题教学，就是以问题为载体，以提出问题、思考问题、解决问题为主线，使学生在设问和释问的过程中萌生学习的兴趣和欲望，进而逐渐养成自主探究和合作交流的学习习惯，并在实践中不断优化学习方法，提高学习能力的一种教学模式.在提出问题、思考问题、解决问题的过程中，获得知识和技能，掌握数学方法，培养探究与合作精神，提升数学素养.

4.4 培养学生概括能力

荷兰数学教育家弗赖登塔尔(h.freudenthal)认为：数学学习的唯一正确方法是让学生进行“再创造”，就是说，由学生本人把学习的东西实现或创造出来，教师的任务是为学生的发展创造条件、引导探索.从教育心理角度讲，所有的新知识、只有通过学生自身“再创造”，使其纳入自己的认知结构中，才能成为有效的知识.数学知识的建构不是一蹴而就，数学教师在教学中不能急以求成，不能像给电脑安装软件一样，将知识“安装”到学生的脑中，或者像焊接工一样将知识“焊接”到学生的脑中，这种方式教学只能让学生机械模仿式的运用，是不能对知识进行提炼和创造性地运用知识，不能有效地对已有的知识系统进行重组和更新，不能提高学生的思维品质.因此，在教学中以问题为载体，通过问题揭示数学知识的发生发展过程，为学生的概括活动搭建平台，千方百计使学生学会概括.特别注意在概括的关键环节上放手让学生自主活动.这种概括活动实际上就是学生数学思维的形成过程，也是数学思想方法的形成过程.数学思维能力是通过数学思想方法为媒介来制约数学思维活动的.所以，在获取数学知识的过程中，注重培养学生的概括能力，实现数学思想方法的形成，以及发展数学思维能力.

1 章建跃.如何学生发现和提出有研究的问题[J].中学数学教学参考,2014(1 /2上)

2 黄严生.注重数学结合，发展学生的思维能力[J].中学数学,2014(8上)

3 [美]G·波利亚.怎样解题[M].上海：上海科技教育出版社,2007新一版

4 [德]Rolf Biheler.数学教学理论是一门科学[M].上海： 上海教育出版社,1998

2015-04-06)