例谈抽象函数的周期性

2015-06-15江苏省如皋中学严循跃邮编226500

中学数学教学 2015年3期

江苏省如皋中学严循跃 (邮编：226500)

解题方法

例谈抽象函数的周期性

江苏省如皋中学严循跃 (邮编：226500)

抽象函数是指没有给出函数的具体解析式，只给出了一些体现函数特征的式子的一类函数．其作为初等数学和近代数学的衔接点，既能体现数学的本质特征，又能体现新课标对知识和技能考核的要求，特别受到高考的青睐．由于抽象函数具有概念抽象、构思新颖、隐蔽性强、灵活性大、综合程度高等特点．而函数的周期性是一类特殊函数的一个重要性质，特别是抽象函数的周期性问题，在学习中不少学生倍感困惑．下面举例介绍几种解决抽象函数的周期性问题，力求使抽象函数周期问题的求解有“法”可依．

1 定义法

函数的周期性定义：若T为非零常数，对于定义域内的任一x，使f(x)=f(x+T) 恒成立，则f(x)叫做周期函数，T叫做这个函数的一个周期．

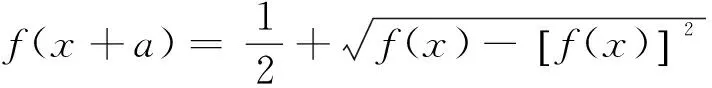
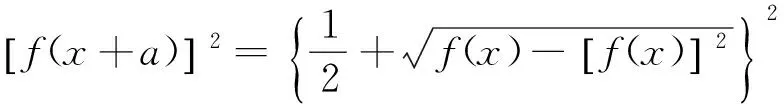
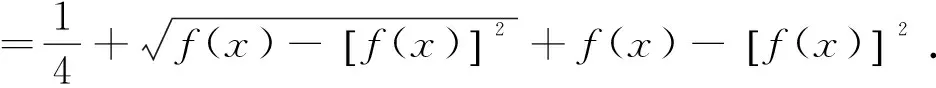
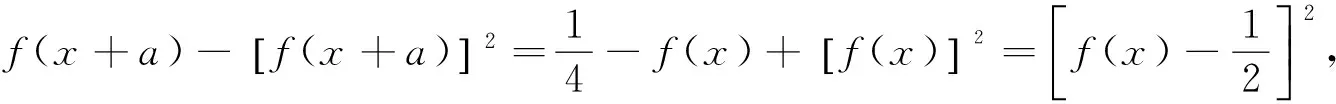
即对∀x∈R，都有f(x+2a)=f(x)成立．所以f(x)为周期函数，且2a是它的一个周期．

注如果题设函数方程中只有一边含有不为零的常数a，另一边与a无关，这时周期T应取决于a，假设T能被a整除，就分别试算f(x+2a)、f(x+3a)、f(x+4a)、…、当出现f(x+T)=f(x)(T≠0)的形式时，就可知T是f(x)的周期．

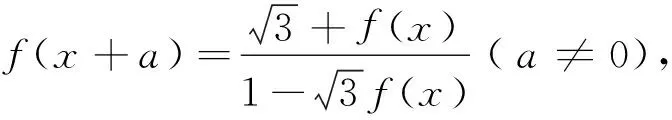
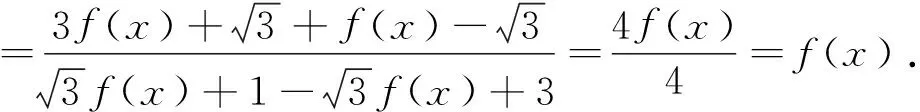
2 变量代换法

对于一些结构较为复杂、变元较多的数学问题，引入一些新的变量进行代换，以简化其结构，从而达到解决问题的目的这种方法叫做变量代换法.

例3 若函数f(x)定义域为R，且对于任意x都有f(5+x)=f(5-x)，f(7+x)=f(7-x)，试问f(x)是不是周期函数．若是，求出它的一个周期；若不是，说明理由．

解在f(5+x)=f(5-x)中以5-x代x得f(x)=f(10-x)

①

在f(7+x)=f(7-x)中以7-x代x得f(x)=f(14-x)

②

由①和②得f(10-x)=f(14-x)，以10-x代x得f(x+4)=f(x)．所以f(x)为周期函数，且4是它的一个周期．

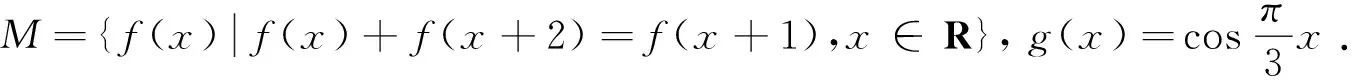
(1)证明：g(x)∈M;

分析对(2)考虑以下两点：①由g(x)是周期为6的周期函数，猜测f(x)也是周期为6的周期函数；

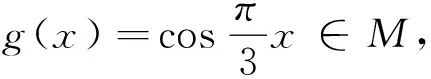
由f(x)+f(x+2)=f(x+1)得f(x+1)+f(x+3)=f(x+2)，从而

f(x)+f(x+2)+f(x+3)=f(x+2)，即f(x+3)=-f(x)，

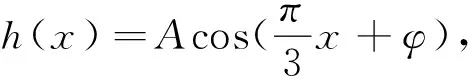
3 特殊值法

通过设题中某个未知量为特殊值，从而通过简单的运算，得出最终答案的一种方法．若问题的选择对象是针对一般情况给出的，则可选择合适的特殊数、特殊点、特殊数列、特殊图形等对结论加以检验，从而做出正确判断．对于有情况讨论的题目，可以代入相应的特殊值，结合排除法进行.这个特殊值必须满足三个条件：首先，无论这个量的值是多少，对最终结果所要求的量的值没有影响；其次，这个量应该要跟最终结果所要求的量有相对紧密的联系；最后，这个量在整个题干中给出的等量关系是一个不可或缺的量．

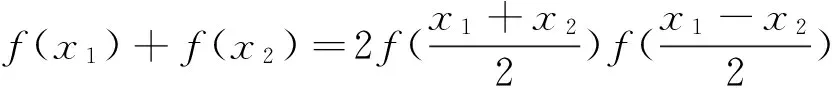
所以令x1=x+π,x2=x，则有

因此可得f(x)是周期函数且有一个周期为2π．

4 递推法

递推法，就是根据题目的特点，构造出递推关系解题的一种方法，解决问题的关键在于构造递推关系．

解由题可知

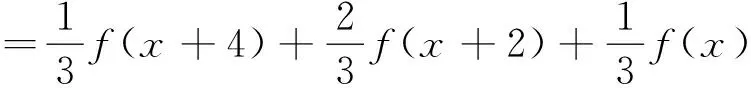
f(x+2)=f(x+4)+f(x)

①

以x+2代换上式x得

f(x+4)=f(x+6)+f(x+2)

②

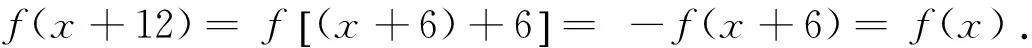
5 结构类比法

在数学教学过程中，我们常常会有“似曾相识”的感觉，而且在不同分支、不同领域中会感到某种类似的成份．如果我们把这些类似进行比较，加以联想的话可能出现许多意想不到的结果和方法，这种把类似进行比较、联想，由一个数学对象已知特殊性质迁移到另一个数学对象上去，从而获得另一个对象的性质的方法就是类比法．它不仅是一种以特殊到特殊的推理方法，也是一种寻求解题思路，猜测问题答案或结论的发现方法．

分析因涉及周期函数，可联想到三角中的和差化积公式