一道2014年高考数学安徽卷试题的推广与简证
2015-06-15安徽省合肥市第六中学周天明邮编230001
安徽省合肥市第六中学 周天明 (邮编:230001)
一道2014年高考数学安徽卷试题的推广与简证
安徽省合肥市第六中学 周天明 (邮编:230001)
文[1]通过对2014年高考数学安徽卷理科第15题的研究,提出了对该题的推广和反思,并对所给的两个推广,利用局部调整法给出了证明.笔者受益匪浅,但美中不足的是文中有一处错误,而且笔者总感觉,文中所给证明方法太过繁琐.经过思考,笔者得到较为简单的证明方法.
推广1 已知两个不相等的非零向量a、b,两组向量x1、x2、…、xm+n和y1、y2、…、ym+n均由m个a和n个b排列而成.(m≤n,m,n∈N+),记S=x1·y1+x2·y2+…xm+n·ym+n,
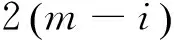

由此,我们不难得到:

②S有m+1个不同的值,分别是S0、S1、…、Sm;


⑤Smax=Sm=ma2+nb2,Smax与a、b的夹角无关;

推广2 已知两个不相等的非零向量a、b,向量x1、x2、…、xm+n由m个a和n个b排列而成.向量y1、y2、…、ym+n由k个a和l个b排列而成.(m+n=k+l,k≤m≤n≤l、k、m、n、l∈N+),记S=x1·y1+x2·y2+…xm+n·ym+n,
由条件可知,x1·y1、x2·y2、…、xm+n·ym+n都只可能取a2,b2,a·b之一,记Si(0≤i≤k,i∈N)为x1·y1、x2·y2、…、xm+n·ym+n中恰有i个取a2时的S.即第一组i个a与第二组的i个a配对,第一组其它m-i个a都与第二组的m-i个b配对,第二组其它k-i个a都与第一组的k-i个b配对,最后第一组剩余的n-k+i个b与第二组剩余的n-k+i个b相互配对.

由此,我们不难得到:

②S有k+1个不同的值,分别是S0、S1、…、Sk;
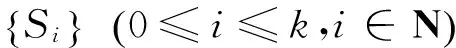

⑤Smax=Sk=ka2+(m-k)a·b+nb2,当m≠k时,Smax与a、b的夹角有关;
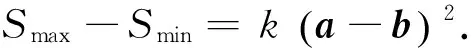
实际上推广1是推广2当m=k时的特列情形.
1 陈良骥.2014年高考数学安徽卷理科第三15题的推广与反思[J], 中学数学教学,2014(4)
2 任志鸿.十年高考分类解析与应试策略[M].海口:南方出版社,2014
2015-01-06)
