多凹点滤波器在LINS中的应用

李汉舟，潘 泉，杨 娜，张娟妮，邓 麟

（1. 西北工业大学 自动化学院，西安 710072；2. 航天科技集团第16研究所 西安710100）

多凹点滤波器在LINS中的应用

李汉舟1,2，潘 泉1，杨 娜2，张娟妮2，邓 麟2

（1. 西北工业大学 自动化学院，西安 710072；2. 航天科技集团第16研究所 西安710100）

分析了激光捷联惯性导航系统中的激光陀螺频谱特性，指出激光捷联惯性导航系统中三个激光陀螺的抖动频率会互相干扰。提出一种多凹点有限冲击响应低通滤波器频域设计方法，通过指定三个抖动频率点幅值为小量，在幅频特性曲线上产生三个凹陷点。该滤波器采用标准滤波算法，同时实现了对激光捷联惯性导航系统三个激光陀螺的滤波和机抖信号的陷波。给出了一个24阶多凹点滤波器设计实例，幅频特性分析说明，由于三个陷波点的集中，该滤波器还可以在机抖频率可能存在的频段上，提供额外的80 dB以上的衰减，可防止激光陀螺抖动频率漂移后陷波性能下降。试验结果表明，多凹点滤波器输出数据波动幅度比原激光捷联惯性导航系统使用的滤波器结果减小5～8倍，三轴摇摆试验的导航精度也有一定提高。

激光捷联惯性导航系统；激光陀螺；有限冲击响应滤波器；陷波；抖动频率

随着激光陀螺动态适应性和精度的提高，激光捷联惯性导航系统（Laser Inertial Navigation System, LINS）逐渐成为高精度惯性导航产品的首选方案[1-3]。为消除闭锁效应，目前工程上广泛采用机械抖动式偏频方案。该方案利用交变的机械抖动机构，对激光谐振腔整体施加高频抖动激励，在机械抖动作用下激光陀螺大部分时间会从锁区内偏置出来，从而减小了闭锁误差[4]。由于机抖频率的存在，激光陀螺输出的有用信号完全淹没在机抖信号中。为了将抖动信号滤除，在LINS导航解算前，关键的一步处理过程为数字滤波，滤波效果好坏直接影响导航解算精度，因此二频机抖激光陀螺信号滤波方法一直是一个研究热点[5-7]。常见的无限冲击响应滤波器(Infinite Impulse Response, IIR)和有限冲击响应滤波器(Finite Impulse Response, FIR)均可以实现这个目的，其中IIR滤波器可以用较低阶实现对机抖频率的较大幅度衰减，运算量小一点，但由于其非线性特点，会对信号造成一定畸变；而FIR滤波器正好相反，欲获得与IIR滤波器相同的衰减幅度，阶数会增大，运算量也会相应增加，但FIR滤波器具有线性相位，不会引起信号畸变。如果运算速度有保障，FIR滤波器更适合激光捷联惯导使用[8]。为了达到较好的滤波效果，FIR滤波器阶数可以设计的很高，但是这会增加系统相位滞后，影响系统动态性能。因此，在实际应用时，应在保证LINS精度的基础上，选择阶数较低的FIR滤波器。

为了提高滤波性能，文献[8]采用零点受阻的自适应IIR陷波器和20阶的FIR滤波器串联的方法，处理中精度激光陀螺单表数据，其效果比达到原40阶FIR滤波器效果。文献[9]使用同样的技术，将IIR陷波器加FIR滤波器串联的滤波方法用于LINS数据处理，因滤波器延迟时间限制，可供选择的FIR滤波器阶数不能大于14，试验证明最终滤波效果比原34阶FIR滤波器差一些。虽然自适应滤波加FIR滤波器效果明显，但是IIR陷波器的引入必定带来信号畸变。为了改进LINS滤波性能，本文提出一种新颖的多凹点FIR滤波器，该滤波器利用FIR滤波器自身产生的凹陷点同时对三个激光陀螺抖动频率进行陷波，可以较低的阶数实现标准FIR滤波，而且不会产生信号畸变，为LINS滤波器设计提供了一个新思路。

1 滤波器指标确定

LINS中有三个陀螺，其抖动频率各不同，在正常工作时，每一个激光陀螺输出信号除了受到自身抖动频率干扰以外，还会受到另外两个激光陀螺抖动干扰。图1给出了高精度LINS保持静止时，三个激光陀螺原始脉冲数据谱分析结果，数据采集频率为2000 Hz。可见，该型激光陀螺抖动频率在300～450 Hz之间。每个激光陀螺输出信号中能量最强的是自身的抖动信号，幅值达到80 dB以上，其它两陀螺抖动信号在谱分析图上也有较强能量集中，约为40 dB左右。在大多数工程应用中，对INS的带宽要求一般在50～100 Hz之间，如果试图把图1中的抖动干扰衰减到0 dB，那么就意味着在3～8倍频程之间，数字滤波器要提供80 dB的衰减，这将使FIR滤波器阶数增加，导致导航计算机运算压力增大，信号相位滞后量增加。因此，在工程实际中，需折中考虑滤波器的阶数和衰减幅度，一般取FIR滤波器阶数为20阶左右，对信号延迟要求不高的系统，FIR滤波器阶数可以取的更高一些。

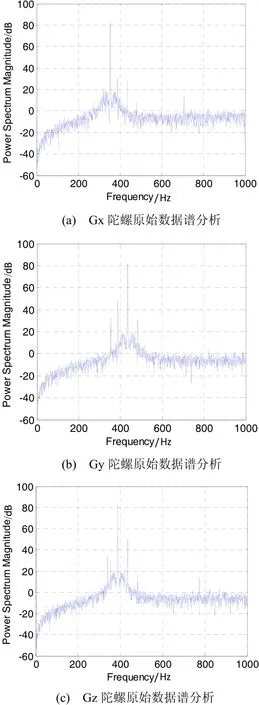
图1 LINS激光陀螺数据谱分析Fig.1 LINS laser gyro power spectrum analysis

图2是一种与该型激光陀螺配套使用的16阶FIR滤波器对Gx陀螺的滤波效果。图2 (a)是滤波前后的时间序列对比情况，由图可见，该滤波器可将抖动幅度从±400 Hz/0.5 ms衰减到±1 Hz/0.5 ms，大部分机抖信号都被滤除。对滤波以后的数据做谱分析见图2(b)，尽管该滤波器为230 Hz以上频率的噪声提供了-60 dB的衰减，但能量最大的抖动干扰（自身抖动频率），绝对幅值仍在+20 dB以上，高于有用信号（直流信号）60 dB；其它两个陀螺抖动信号也依然明显存在，只是被衰减到-20 dB以下。这说明通过该FIR滤波以后，激光陀螺输出数据中还存在较强能量的抖动信号成份。因为机抖信号幅度具有一定随机性，所以这些残存的机抖噪声不仅带来不稳定性噪声，而且在导航解算时还会产生伪圆锥误差和划桨误差，影响导航精度。

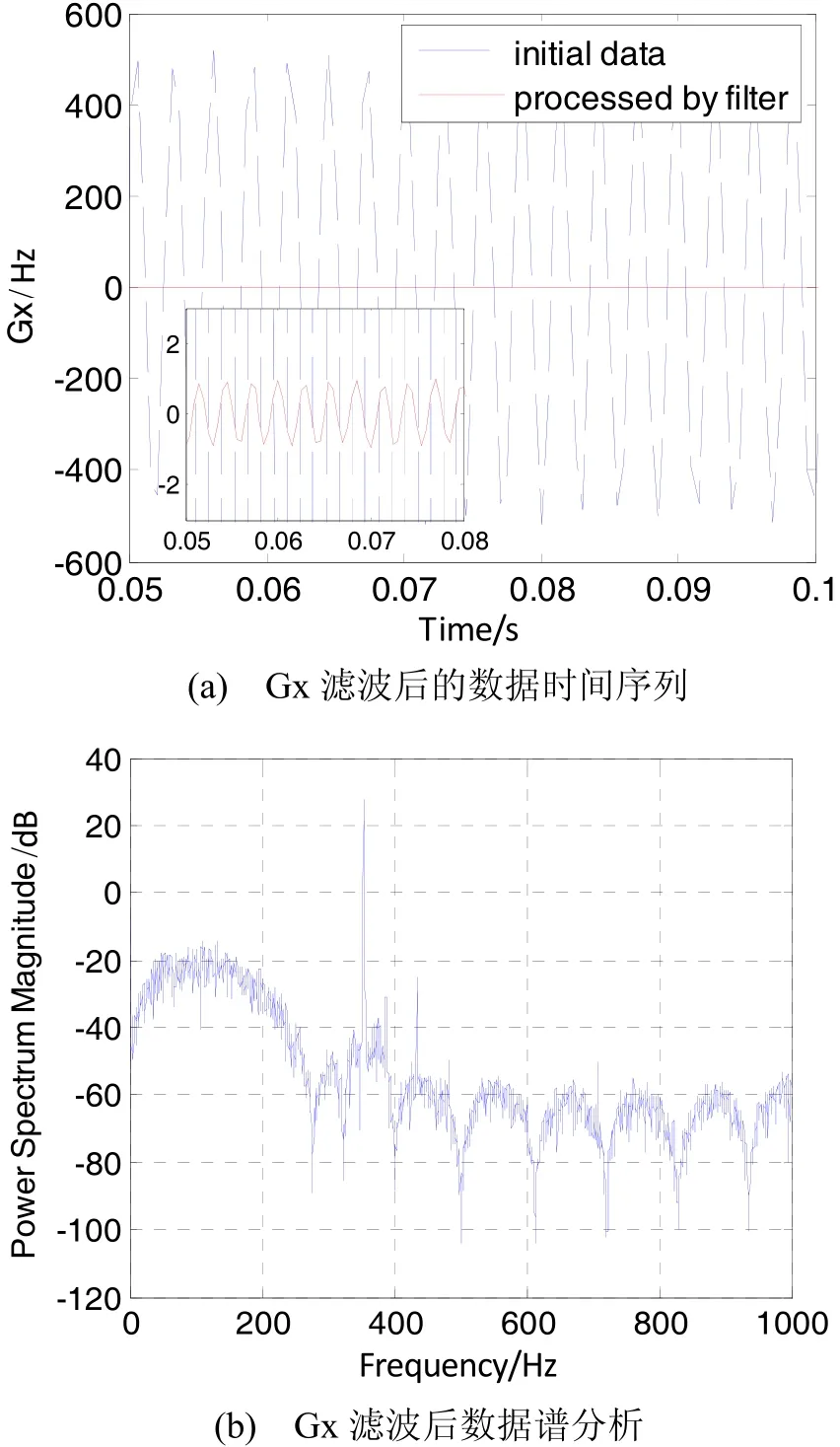
图2 原FIR滤波器对Gx陀螺滤波效果Fig.2 Results of Gx gyro data processed by the old filter

为了进一步抑制抖动带来的干扰，可以考虑采用陷波器处理机抖信号。但由FIR陷波器设计原理的限制，用FIR实现陷波功能其效率并不高，比如：如果要得到一个在300～450 Hz具有-60 dB陷波能力的FIR陷波器，其阶数将到达30阶以上。因此，直接采用FIR陷波器会导致LINS输出信号相位滞后大幅增加。一个比较好的思路是在设计FIR滤波器时，把FIR滤波器的梳状凹陷点配置到机抖频率上，利用FIR滤波器的天然凹陷点实现陷波功能，从而在LINS滤波的同时给机抖频率点处增加额外的衰减能力。

从目前已有的FIR滤波器设计方法来看，通过微调滤波器参数，可以将FIR滤波器形成的天然凹陷点对准一个陀螺的机抖频率点，但是无法将三个凹点同时对准三个陀螺的机抖频率。因此，摆在设计师面前的问题是：如何用较少的阶数，设计一个FIR滤波器，具有低通滤波特性的同时对三个机抖频率点做陷波处理。根据LINS激光陀螺谱分析结果，这种多凹点FIR低通滤波器设计目标为：采样速率2000 Hz或更高，滤波器带宽100 Hz左右，阻带起始频率小于300 Hz，阻带衰减不少于60 dB，在阻带衰减基础上还应对三个机抖频率点额外提供不小于80 dB的衰减。

2 多凹点FIR滤波器设计

FIR滤波器设计方法很多，常见的有窗函数法，频率取样法，最小二乘法，最优等纹波法。本文试验采用的高精度LINS数据采样频率2000 Hz，带宽大于80 Hz，带宽与采样频率比值为1/25，属于典型的窄带滤波问题。频率取样法对于这种通带宽度小于1/5窄带低通滤波器设计非常适合，具有其它设计方法不能代替的优点；另外，三个激光陀螺抖动频率已知，用频率取样法可以很方便地设计陷波点位置。因此，本文采用频率取样法设计LINS的多凹点FIR滤波器。

传统FIR滤波器的频率取样法设计基本思路为：根据要求的理想频率响应Hd(f)选定N个取样值H(k)，计算H(k)的N点离散傅里叶逆变换就会得到滤波器..。本文在设计多凹点FIR滤波器时，在三个机抖频率处增加三个频率取样点，并令其幅值为小值，这样就在三个指定频率点形成三个陷波器。滤波器设计方法如下：

设目标滤波器带宽为fbw，阻带起始频率为fss，三个陀螺抖动频率为fGx、fGy、fGz，采样频率为fs＞2Max(fGx,fGy,fGz)，滤波器初始阶数为M1。先在频率[0,fs/2]上采集K个频率点的幅值，其中包含一个过渡带频率点fa∈(fbw,fss)，过渡带的幅值设为a, a∈(0,1)：

式中：

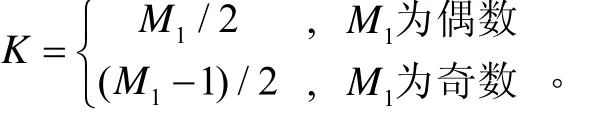
在此基础上，对三个抖动频率fGx、fGy、fGz也进行采样，并与(1)的采样点合并，共计得到K+3个采样频率点。根据第一大类FIR滤波器对称性，可得滤波器阶数上升为

式(1)进一步表示为

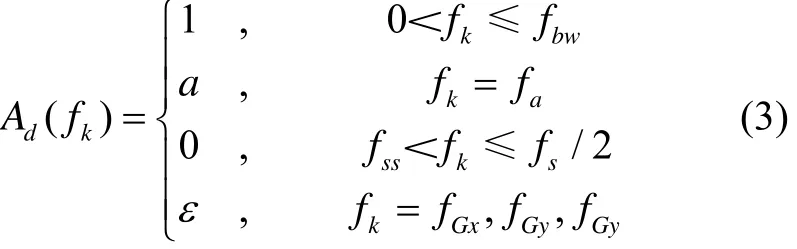
式中，ε为小量。则在这些采样点的相位响应为

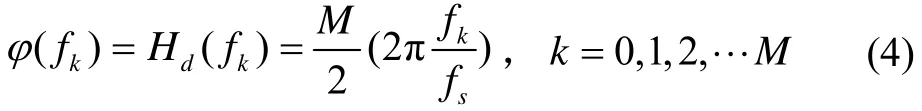
于是得到频域采样的幅值序列：

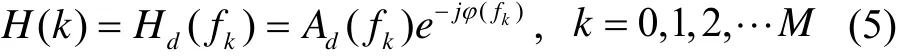
由离散傅里叶逆变换就可以得到h(n)：

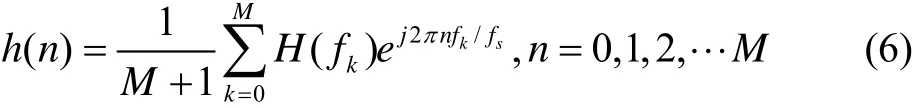
以上步骤基本为标准过程，已有众多文献介绍，在此不再赘述。在此给出一个设计实例，已知LINS三个激光陀螺机抖频率分别为335.4 Hz、375.5 Hz、425.7 Hz，采样频率2000 Hz，设计一个24阶多凹点滤波器，由公式(1)～(6)得其系数矩阵为：

h(n)=[-3.6162e-4 -5.5582e-5 -4.6181e-4 1.3181e-3 4.3263e-3 1.1456e-2 2.3008e-2 3.9629e-2 6.0210e-2 8.2250e-2 1.0213e-1 1.1603e-1 1.2103e-1 1.1603e-1 1.0213e-1 8.2250e-2 6.0210e-2 3.9629e-2 2.3008e-2 1.1456e-2 4.3263e-3 1.3181e-3 -4.6181e-4 -5.5582e-5 -3.6162e-4]。

滤波器单位冲击响应见图3(a)，可见这是一个奇对称滤波器，属于第一大类偶数阶正对称FIR滤波器，具有线性相位。图3(b)是该滤波器和原来使用的16阶FIR滤波器幅频特性对比。由图可见，两个滤波器带宽都大于80 Hz，在200 Hz以内幅频特性曲线基本重合，而多凹点滤波器在每一个抖动频率点有一个陷波点，陷波点绝对深度大于150 dB，保证滤波器同时对三个机抖频率具有强烈抑制作用。除此以外，在300 Hz～450 Hz之间的150 Hz频带范围内（也就是机抖频率可能存在的频率范围），由于陷波点的集中，额外形成一段80～100 dB的连续凹陷区域，该连续凹陷区域可以在激光陀螺机抖频率温漂（由于自身发热和环境温度变化，激光陀螺机抖频率会在±5 Hz内随时间漂移[8]）情况下，持续提供80～100 dB额外的衰减幅度(大于图1所示的80 dB抖动能量峰值）。因此，本文提出的多凹点滤波器即便在三个抖动频率都产生漂移后，仍然能够很好地抑制抖动干扰。当然，由于对滤波器有了更多的约束条件，这种多凹点滤波器阶数会增加，从而导致信号延迟增加。但从设计实例来看，多凹点滤波器阶数也是20阶左右，满足一般LINS需要，也比文献[8]和[9]中的30～40阶FIR滤波器阶数还是低很多。

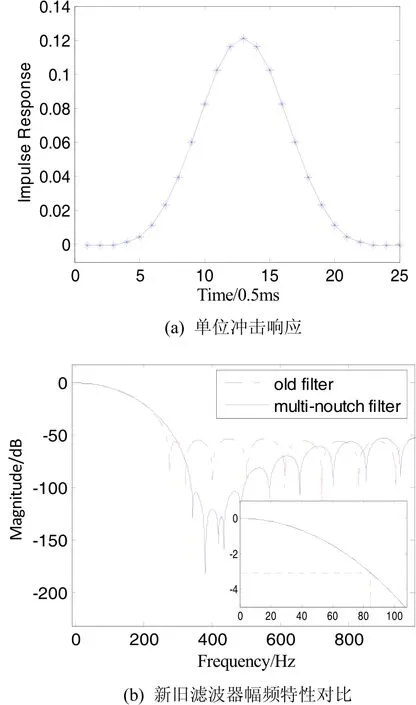
图3 多凹点滤波器设计结果Fig.3 Design results of multi-notch filter

3 滤波效果分析

3.1 原始数据滤波效果分析

采用与图2相同的原始试验数据，分别用多凹点滤波器与原16阶滤波器进行滤波处理，效果对比情况见图4。可见多凹点滤波器使得Gx陀螺输出数据波动幅度比原16阶滤波器输出结果波动幅度下降5～8倍，与文献[8]中的40阶FIR滤波器，或IIR自适应陷波加20阶FIR滤波器效果相当。与该文相比，本文滤波算法为标准FIR滤波器滤波算法，更为简单一些，而且不会产生信号畸变。图4(b)是对Gx陀螺滤波后的时间序列谱分析结果，对比图2(b)可见，在图2(b)中最大的残存机抖能量大于+20 dB，而在图4(b)中最大的残余机抖能量小于-80 dB，这说明本文提出多凹点滤波器可将LINS中的三个激光陀螺机抖频率能量衰减到原滤波器的1/105，因此具有更强的滤波性能。

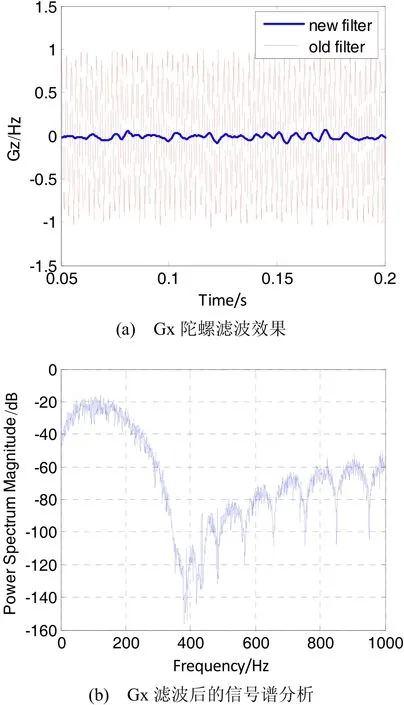
图4 多凹点FIR滤波器效果Fig.4 Results of Gx gyro data processed by the multi-notch filter

3.2 导航精度分析

圆锥误差是LINS的主要动态误差。如果对激光陀螺机抖频率滤除不彻底，在LINS中三个激光陀螺的机抖频率会互相耦合，将形成伪圆锥误差[4]。为了验证本文设计的多凹点滤波器滤波效果，本文采用一套导航级LINS（激光陀螺精度0.007 (°)/h，加速度计精度5×10-5g），进行三轴摇摆，以便在三个轴上均激励出圆锥误差，考察多凹点滤波器抑制机抖频率以后LINS的导航精度变化情况。

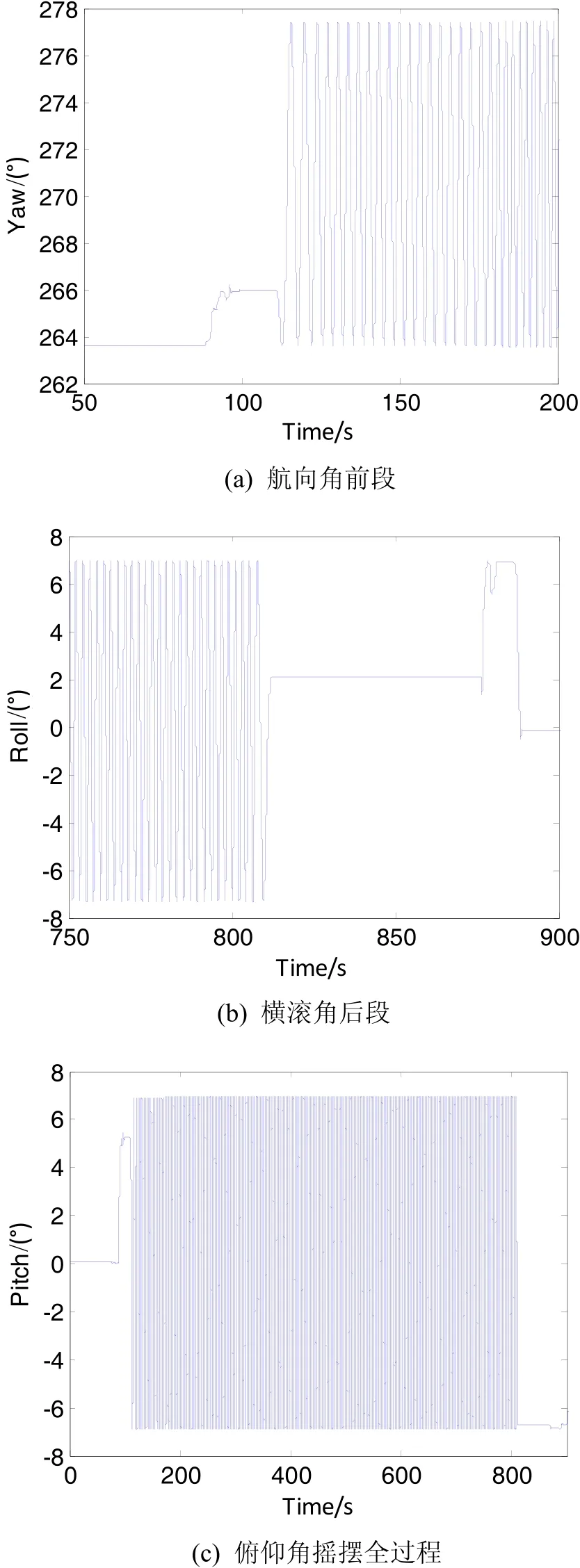
在进行摇摆试验时，将LINS安装在三轴摇摆台的内框上，首先保持LINS静止5 min，用于自对准，然后以7° 0.5 Hz进行三轴摇摆10 min，以2000 Hz记录未经滤波的原始脉冲数据，分别采用原16阶FIR滤波器和本文提出的多凹点FIR滤波器处理数据，然后进行导航解算，试验结果如图5所示。图5(a)、(b)、(c)是多凹点滤波器滤波后姿态更新结果，图5(a)给出了摇摆台电机逐渐加速过程，随着电机加速，航向曲线频率趋于稳定；图5(b)是试验结束时横滚角曲线；图5(c)是俯仰角摇摆试验全过程曲线。图5(d)和(e)则给出了两种滤波算法处理后的速度曲线和位移曲线对比情况。可见在本次试验中，多凹点滤波器处理后的数据速度漂移和位置漂移比原滤波器减小，水平定位误差由原来的 1537 m下降到1386 m，精度提高10%左右，这说明多凹点滤波器可以更好地抑制抖动频率对导航解算带来的误差。

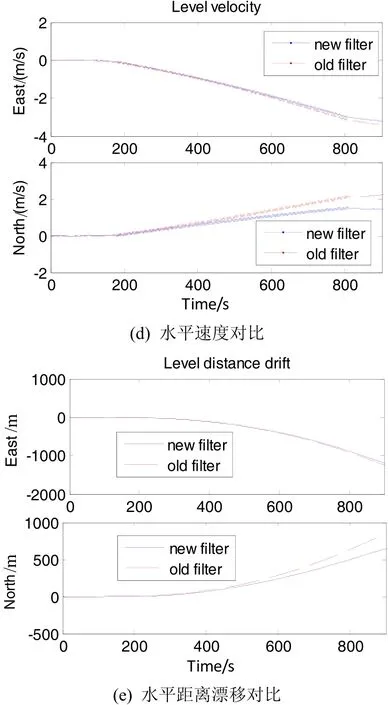
图5 多凹点FIR滤波后的跑车试验导航结果Fig.5 Vehicle navigation results after LINS data processed by the multi-notch filter

4 结 论

本文针对LINS中同时存在三个激光陀螺抖动信号干扰问题，提出了一种多凹点FIR滤波器设计方法，采用标准FIR滤波算法，可以在实现低通滤波的同时将三个陀螺的抖动信号滤除。该滤波器保持了FIR滤波器的线性相位特点。另外，由于三个凹点相对集中，多凹点滤波器在激光陀螺抖动频率可能存在的频段范围内形成一个额外的陷波段，能够在激光陀螺抖动频率产生温度漂移情况下，仍然保持较好的滤波效果。滤波试验和导航试验结果都说明，该滤波器对降低激光陀螺陀螺数据输出波动幅度和提高LINS导航精度都有一定作用。

（References）：

[1] Peshekhonov V G. Gyroscopic navigation systems: current status and prospects[J]. Gyroscopy and Navigation, 2011, 2(3): 111-118.

[2] Golyaev Y D, Kolbas Y Y. Application of ring laser to determine the directions to the poles of Earth’s rotation[J]. Quantum Electronics, 2012, 42(10): 949-952.

[3] Sanders S J, Strandjord L K, Mead D, et al. Fiber optic gyro technology trends - a Honeywell perspective [C]//15th Optical Fiber Sensors Conference Technical Digest, Portland, USA, 2002: 5-8.

[4] 王宇. 机抖激光陀螺捷联惯导系统的初步探索[D]. 长沙: 国防科技大学, 2005: 1-60. Wang Yu. Research on inertial navigation system with mechanically dithered ring laser gyroscope[D]. Changsha, P.R.China, Graduate School of National University of defense Technology, 2005: 1-60.

[5] 李春, 韩军海. FIR 硬件滤波技术在激光陀螺中的应用[J]. 中国惯性技术学报, 2013, 21(6): 817-821. Li Chun, Han Jun-hai. Technology of FIR filtering based on FPGA[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 817-821.

[6] Hua Chun-hong, Ren Zhang, Zhang Min-hu, et al. Filtering of long-term dependent fractal noise in fiber optic gyroscope[J]. Journal of Systems Engineering and Electronics, 2010, 21(6): 1041-1045.

[7] Rachu P. On adaptive IIR lattice notch filter using a robust variable step-size for the detection of sinusoid[C]// The 8th International Conference on Communication Systems. Dept. of Telecommun. Eng., Mahanakorn Univ. of Technol. Bangkok, Thailand, 2002, Vol.2.

[8] 晁志超. 二频机械抖动激光陀螺信号处理算法的研究[D]. 长沙: 国防科技大学, 2006: 12-42. Chao Zhi-chao. Research on signal processing algorithm of mechanically dithered gyroscope[D]. Changsha, China: Graduate School of National University of Defense Technology, 2006: 12-42.

[9] 程耀强, 徐德民, 万彦辉, 等. 基于数字滤波的激光陀螺数字信号处理算法[J]. 中国惯性技术学报, 2013, 21(1): 112-115. Cheng Yao-qiang, Xu De-min, Wan Yan-hui, et al. Digital signal processing algorithm of laser gyro based on digital filter[J]. Journal of Chinese Inertial Technology, 2013, 21(1): 112-115.

Multi-notch filter application in laser inertial navigation system

LI Han-zhou1,2, PAN Quan1, YANG Na2, ZHANG Juang-ni2, DENG Lin2
（1. College of automation, Northwestern Polytechnical University, Xi’an 710100, China; 2. The 16th Institute of China Aerospace Science and Technology Corporation, Xi’an 710100, China)

The power spectrum characteristics of ring laser gyros in laser inertial navigation system (LINS) are analyzed, which suggests that three laser gyros’ dithering frequencies will interfere with each other in LINS. A novel low-pass finite impulse response (FIR) filter with three-notch is proposed to filter the dither frequencies of the ring laser gyros. A multi-notch FIR filter is designed with frequency-domain design method by specifying the amplitude of three dithering frequencies to be a small quantity. Three notches are produced naturally in the FIR amplitude frequency characteristic curve. The filter adopts a standard FIR algorithm. Meanwhile, the low-pass filter for the three laser gyros’ signal in LINS and notching for the dithered signal are realized. A 24-order multi-notch FIR filter is given as an example to process the data of a high-precision LINS. The amplitude-frequency characteristic analysis shows that the new filter provides extra attenuation by at least 80 dB in the possible dithering frequency band due to three notch points concentrated. The extra decay can effectively prevent the filter performance degradation due to the laser gyro’s dithering frequencies drift. Experiments suggest that the data oscillation of the output from the new filter is decreased by 5～8 times compared with that of the old filter in the LINS. Furthermore, the three-axis wobbling test results show that the navigation precision can also be improved.

laser inertial navigation system; laser gyro; finite impulse response filter; notch filter; dither frequency

U666.1

A

1005-6734(2015)04-0451-06

10.13695/j.cnki.12-1222/o3.2015.04.007

2015-04-18；

2015-07-16

国家自然科学基金重点项目（61135001）

李汉舟（1973—），男，博士，研究员，从事高精度惯性导航系统、数字信号处理、陀螺寻北仪等研究。Email：mr_lihanzhou@sina.com