双陷波补偿算法在火箭推力矢量控制中的扩展应用
2016-06-05幺志刚卢红影周海强
孙 毅,幺志刚,卢红影,李 昌,周海强
双陷波补偿算法在火箭推力矢量控制中的扩展应用
孙 毅,幺志刚,卢红影,李 昌,周海强
(北京精密机电控制设备研究所,北京,100076)
针对单陷波补偿算法滤波带宽较窄的问题,提出将双陷波补偿算法应用于单谐振点发动机伺服机构控制并建立了数学模型。仿真结果表明,双陷波补偿算法能够在较宽范围内相对有效地抑制谐振峰,且其低频段相角与单陷波补偿算法相比滞后并不明显。为验证分析的正确性,在试验台上对伺服机构进行陷波补偿算法试验,为双陷波补偿算法在火箭推力矢量控制中的扩展应用奠定基础。
伺服机构;双陷波补偿;谐振峰
0 引 言
物质的固有频率与其振动频率接近时,容易发生共振现象。火箭发动机也是如此,但其谐振现象更加复杂,因为火箭发动机不仅刚度分布不均且转动惯量较大,只能由伺服机构承担抑制谐振的任务(通过伺服机构扫频测试,得到角位移与线位移输出频率特性,再进行比较运算,即可得到发动机的谐振特性)[1~3]。对伺服机构采用陷波补偿控制算法或采用具有动压反馈的伺服阀是常用的抑制负载谐振的有效手段[4~6]。与动压反馈相比,陷波补偿算法能够省去压差传感装置,不仅具有成本控制的优势,而且参数调节灵活,采用陷波补偿算法抑制负载谐振是未来发展的方向。
在运载火箭的研制过程中,发现有些火箭发动机的频率值在某一范围内仅有一个谐振峰,即仅具有一个固有频率,而有些液体火箭发动机的频率值在某一范围内会出现2个谐振峰,即具有2个固有频率,对于后者而言,如果采用单陷波的凹口补偿算法已不能对具有2个谐振峰的谐振进行很好地抑制,于是出现了双凹口的陷波补偿算法[1];对于具有双谐振点的发动机而言,仿真和试验证明双陷波补偿算法更适于伺服机构的谐振抑制,可以有效地控制不同频段的幅值和相角。
然而将双陷波补偿算法扩展应用于仅具有单个谐振峰的火箭发动机的伺服机构负载谐振抑制中会产生何种效果,尤其是在单陷波补偿算法因滤波带宽较窄而无法在大范围频段内有效抑制谐振峰的情况下,对于这一问题国内外较少研究。本文以此为出发点,对仅具有单个谐振点的发动机伺服机构的控制分别进行单点陷波和双点陷波补偿算法的仿真和试验,并对二者造成的影响进行分析和比较,为双陷波补偿算法在火箭推力矢量控制中的扩展应用奠定基础。
1 控制模型
某Ⅰ级大功率伺服机构与发动机负载模拟台的联接方式如图1所示。由图1可知,箭上计算机将控制指令发送至伺服机构,伺服机构的活塞杆根据控制指令要求产生位移(伸、缩),驱动发动机喷管(或模拟负载)摆动,改变推力矢量方向,实现姿态稳定与控制。

图1 伺服机构与发动机的联接方式
图2为采用单陷波补偿算法的火箭发动机伺服机构的控制回路模型。由图2可知,箭上计算机输入位置指令至控制器,位置指令在控制器中进行算法补偿并转换成电流信号,电流信号作用于伺服阀并控制伺服阀的输出流量,从而驱动伺服机构的活塞运动。反馈电位计将活塞的位移转换为电压信号,反馈到数字伺服控制器,由伺服控制器完成输入指令与位移反馈信号的综合,实现数字闭环,控制伺服作动器执行相应动作[7,8]。
图2中采用的是最基本的单陷波补偿环节,传递函数为
陷波补偿的原理是将式(1)中零、极点替换,即把低阻尼比的一对极点和替换为较高阻尼比的另外一对极点和,从而改善系统的稳定性[1]。
采用双陷波补偿算法时,对应的传递函数为
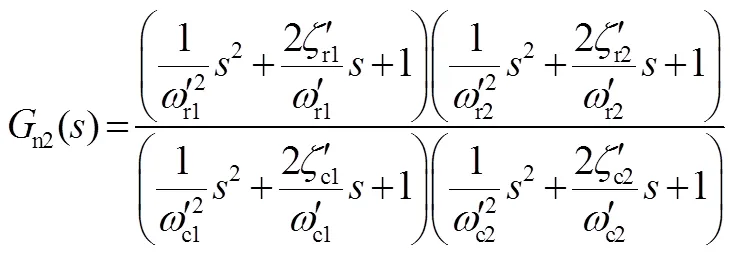
双陷波补偿算法的伺服机构控制回路模型如图3所示。比较图3与图2可以看出,除了补偿算法的区别外,图3和图2只有作动器的负载效应和发动机的负载特性不同。若将双陷波补偿算法应用于仅具有单个谐振峰的火箭发动机的伺服机构控制回路中,则此时的模型如图4所示。

图2 单陷波补偿算法在单谐振点发动机伺服机构控制中的模型

图3 双陷波补偿算法在双谐振点发动机伺服机构控制中的模型
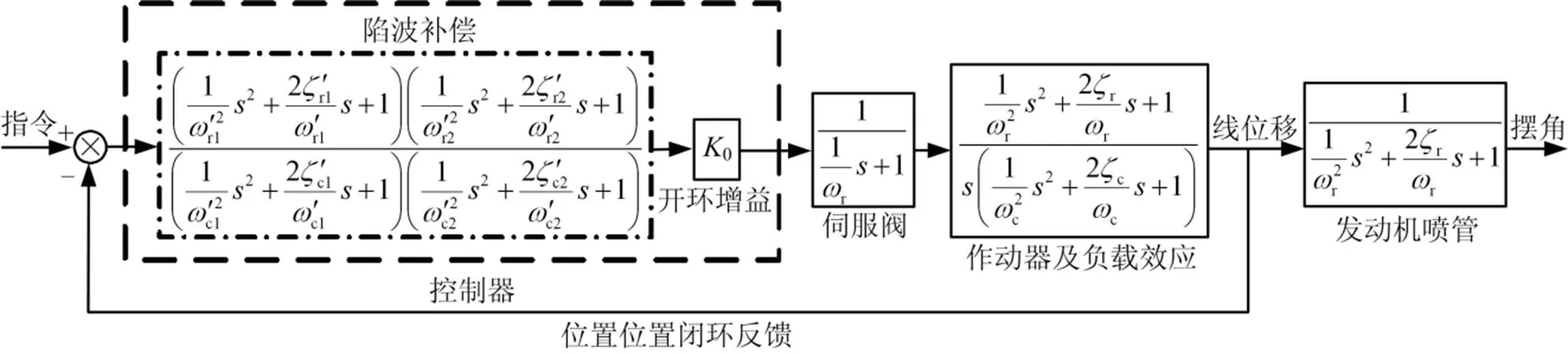
图4 双陷波补偿算法在单谐振点发动机伺服机构控制中的模型
2 仿真分析
根据上述伺服机构控制模型,对仅具有单个谐振峰的火箭发动机的伺服机构频率特性进行仿真,并将加入单陷波补偿前、后伺服机构的频率特性曲线进行比较,如图5所示。

a)幅频
b)相频
图5 加入单陷波补偿前、后伺服机构的频率特性
由图5a可看出,未加校正系统的幅值在低频段时基本保持不变,之后略有下降,再出现一个明显凸起的谐振峰,单陷波补偿校正的作用是在出现谐振峰的频段区通过产生一个幅值凹陷点抵消谐振峰,可以看出校正后的系统在高频段的幅值得到明显地抑制。由图5b可看出,在加入单陷波补偿算法后系统相角较未加补偿前出现不同程度的滞后,说明单陷波补偿算法对相位特性有负面影响。由此可见,将单陷波补偿算法应用于仅具有单个谐振峰的火箭发动机的伺服机构负载谐振中的方法有效,但不能同时改善相角和幅值。
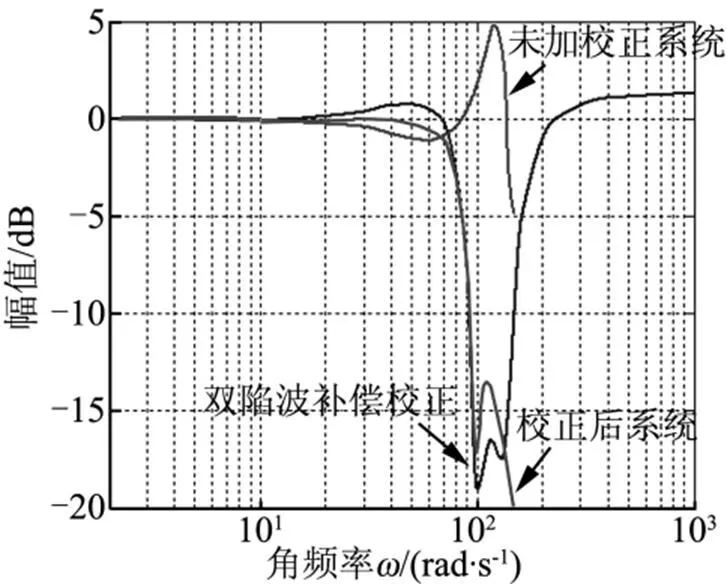
图6为加入双陷波算法补偿校正前、后伺服机构带载的频率特性曲线。由图6可以看出,双陷波算法补偿校正的原理与单陷波算法补偿校正相似,同样是在谐振峰对应的频段范围内以幅值凹陷的形式抵消谐振峰,但与单陷波补偿不同的是凹陷区有2个凹点,并且相位曲线中有2个明显的凸起滞后点。
a)幅频
b)相频
图6 加入双陷波补偿前、后伺服机构的频率特性
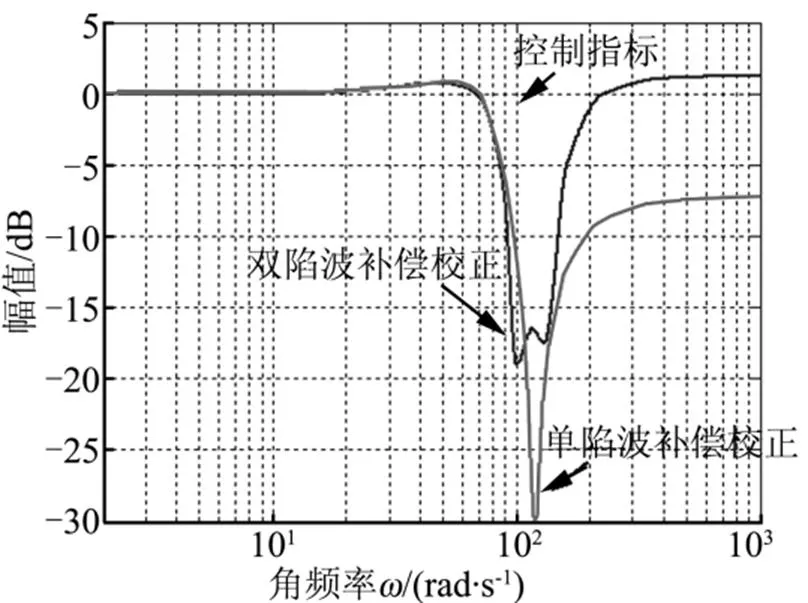
为了对单陷波补偿和双陷波补偿的效果更直观地比较,将单陷波补偿与双陷波补偿算法放在一起进行区分,如图7所示。
从图7a可以看出,双陷波补偿算法有2个凹点,且凹陷区最底端由2个凹点形成的宽度要明显大于单谐振补偿算法的凹陷区由一个凹点形成的宽度,这说明相同条件下双陷波补偿算法能够在更宽的频段范围内对系统的幅值进行抵消和抑制。但由于2个凹点的深度均较单陷波补偿算法的单凹点浅,因此就谐振频率点的补偿效果而言,双陷波不如单陷波补偿算法。从图7b可以看出,当低频段时单、双陷波补偿算法的区别不大,但当进入中频段之后双陷波补偿比单陷波补偿的相角滞后会有所增加,此时单陷波补偿算法的相角指标较双陷波补偿变优,高频段时双陷波补偿和单陷波补偿的相角均大幅上扬,此时不具有应用意义。
a)幅频
b)相频
图7 单、双陷波补偿对伺服机构的频率特性
3 试验验证
为验证理论分析和仿真的正确性,利用发动机喷管负载模拟台对单谐振点负载条件下的伺服机构控制算法进行试验,分别采用单陷波补偿算法和双陷波补偿算法并对二者进行比较,得到负载模拟台实测角位移频率特性试验曲线,如图8所示。

a)幅频
b)相频
图8 角位移频率特性
由图8可以看出,经过陷波补偿算法后的幅值在高频段的衰减较仿真曲线更明显,说明实际陷波补偿中对幅值的抑制作用比仿真中的还要明显。这是因为对伺服机构控制模型中的某些模块进行了简化,并且个别参数设置的准确性还有待进一步提高,但总的来说试验曲线和仿真曲线的趋势是一致的。
双陷波补偿较单陷波补偿能够在更宽的范围内对系统谐振点附近的幅值产生抑制作用,但就谐振点而言,单陷波补偿的抑制效果比双单陷波补偿明显;在相位的滞后性上,单陷波补偿优于双陷波补偿,但二者在低频段的区别并不明显。
4 结 论
针对单谐振点发动机难以将谐振点准确定位的问题,提出将双陷波补偿算法应用于单谐振点发动机伺服机构控制的研究方法,扩展了双陷波补偿算法在火箭推力矢量控制中的应用范围,建立了双陷波补偿算法在单谐振点发动机伺服机构控制中的数学模型,并就双陷波和单陷波的补偿效果进行了仿真和试验。结果表明:双陷波补偿较单陷波补偿能够在更宽的范围内对系统谐振点附近的幅值产生抑制作用,但就谐振点而言,双陷波补偿的抑制效果不如单陷波补偿明显,在相位的滞后性方面,单陷波补偿优于双陷波补偿,但二者在低频段的区别并不明显。
[1] 尹传威, 赵守军, 陈克勤. 双谐振点发动机推力矢量控制伺服机构算法优化研究[J]. 导弹与航天运载技术, 2013(1): 21-26.
[2] 黄效国, 程建中, 崔勇. 使用软件动压反馈提高大惯性负载液压伺服系统稳定性[J]. 液压与气动, 1994(4): 10-13.
[3] 赵迎鑫. 大运载助推级伺服机构真实发动机负载动态模型的获取和辨识[C]. 北京: 第五届全国流体传动与控制学术会议, 2008.
[4] 蔡璞, 许化龙, 夏克寒. 导弹液压伺服系统中陷波器的原理与设计[J]. 导弹与制导学报, 2006, 26(2): 148-149.
[5] 黄翔东, 王兆华, 吕卫. 陷波频率点可精确控制的高效FRM陷波器设计[J]. 系统工程与电子技术, 2009, 31(10): 2320-2322.
[6] 黄效国, 程建中, 崔勇. 使用软件动压反馈提高大惯性负载液压伺服系统稳定性[J]. 液压与气动, 1994(4): 10-13.
[7] 叶宏, 曾广商. 三余度数字伺服控制系统建模与动静态特性研究[J]. 固体火箭技术, 2003, 26(1): 71-75.
[8] 曾广商, 沈为国, 石立, 张晓莎. 高可靠三冗余伺服机构系统[J]. 航天控制, 2005(1): 35-40.
Research on Extended Application of Double-notch Compensation Algorithm for Rocket Thrust Vector Control
Sun Yi, Yao Zhi-gang, Lu Hong-ying, Li Chang, Zhou Hai-qiang
(Beijing Institute of Precision Mechatronics and Control Equipment, Beijing, 100076)
Aiming at the problem of single-notch with narrow bandwidth, a double-notch compensation algorithm was applied to the servo-mechanism of single resonance engine. The mathematical model of the double-notch filter was established. Simulation results showed that the resonance peak was effectively inhibited, and the phase delay was improved compared to the single-notch filter. Experiments on notch compensation algorithm were carried out at test rig to verify the simulation model, and laid the foundation for the application of double-notch compensation algorithm on rocket thrust vector control.
Servo-mechanism; Double-notch compensation; Resonance peak
1004-7182(2016)03-0077-04
10.7654/j.issn.1004-7182.20160318
V433
A
2016-01-05;
2016-03-15
孙 毅(1979-),男,博士,工程师,主要研究方向为液压元件与系统的优化设计
