航位推算组合导航系统在线标定技术

刘永红，刘明雍，谢 波

（1. 西北工业大学 航海学院，西安 710072；2. 航天第十六研究所，西安 710100）

航位推算组合导航系统在线标定技术

刘永红1，刘明雍1，谢 波2

（1. 西北工业大学 航海学院，西安 710072；2. 航天第十六研究所，西安 710100）

在航位推算组合导航系统中，存在里程计安装偏差角误差和标度因数误差。推导了里程计安装偏差角误差和标度因数误差对航位推算速度和位置精度的影响，并提出了一种航位推算组合导航系统在线标定算法。该算法利用航位推算的速度与GPS的速度之差作为速度量测，航位推算的位置与GPS的位置之差作为位置量测，对航位推算组合导航系统的姿态误差、安装偏差角误差和标度因数误差进行有效估计，并通过仿真试验和车载试验对该算法的有效性进行了验证。试验结果表明，通过车载试验在线标定出的里程计各误差参数与里程计传统标定法标定的结果接近，且该算法计算量小，具有一定的工程应用价值。

航位推算；组合导航；安装偏差；标度因数

随着现代战争模式的发展，越来越多的军用特种车辆开始装备车载导航系统。激光捷联惯导系统具有自主性强、隐蔽性好、精度高，且可以提供完整的导航信息（位置、速度、姿态）等优点，在车载导航系统中得到了广泛应用。但激光捷联惯导系统误差会随时间积累，组合导航是减小激光捷联惯导系统导航误差的有效手段，因此近年来SINS/GPS车载组合导航技术得到了较深入的研究和广泛的应用。但GPS信号质量受外界环境影响较大，而且受制于人，可靠性较差，不能完全依赖。里程计可以在GPS失效时作为惯导系统的辅助信息源，同时还可与惯导系统构成航位推算组合导航系统，可使车载导航系统导航精度得到保障。

实际应用中激光捷联惯导系统难以与载车坐标系重合，因此存在着里程计安装偏差。里程计安装偏差和标度因数误差是制约航位推算系统精度的关键参数。载车在行进过程中安装误差角特别是俯仰安装误差角的大小容易发生变化，而里程计标度因数误差与载车车轮气压和路面状况等因素有关[3]。文献[1]只对里程计标度因数误差进行了估计，文献[2-3]虽然对里程计安装俯仰角误差、安装偏航角误差和标度因数误差都进行了估计，但模型较复杂。本文对车载航位推算组合导航算法进行了简化，并通过仿真试验和车载试验对该算法进行验证。

1 航位推算误差分析

假设里程计坐标系记为m系，它的oy轴在与载车车轮相接触的地平面内，并且指向车体的正前方，oz轴垂直于地平面向上为正，ox轴指向右方，即里程计坐标系为右-前-上（RFU）坐标系。实际应用中捷联惯导系统难以与载车坐标系重合，因此b系和m系之间存在安装偏差角。假设航向安装偏差角为aφ，俯仰安装偏差角为aθ，横滚安装偏差角ar，并假设它们都是小角。类似于求解捷联惯导姿态矩阵的方法，依次经过aφ、aθ和ar三次转动，可得从b系到m系的变换余弦阵为[5]

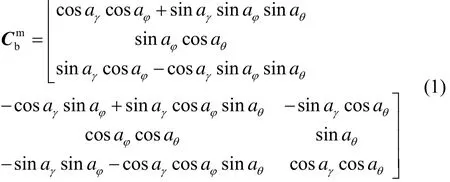
令α=[aθaγaφ]，则实际的b′系与m系之间的坐标变换矩阵可表示为

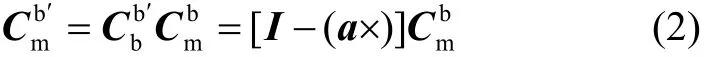
里程计的测量误差主要由标度因数误差引起，假设里程计标度因数误差为δKD，则里程计测量的速度表达式为

式中，Dυ为实际速度。则将车体坐标系下里程计的速度投影到导航坐标系下有

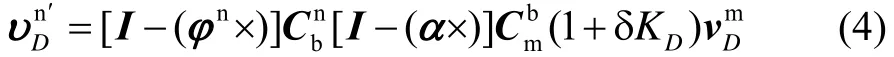
式中，nφ为捷联惯导系统解算的姿态误差角。将式(4)展开并忽略高阶小量得

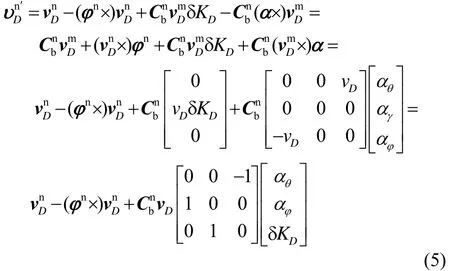
由式(5)可知，αγ对里程计的速度没有影响，因此该系统中只需考虑αθ、αφ和δKD的影响。

令∂=[aθaφδKD]T，则有[3]：

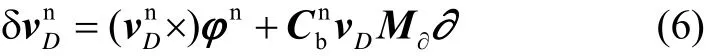
结合捷联惯导系统的位置误差方程可得到航位推算定位误差方程：

2 航位推算组合导航在线标定算法

假设捷联惯导系统中惯性器件的刻度因数误差、安装误差已事先标定，并已进行了工具误差补偿，则航位推算组合导航姿态误差方程为

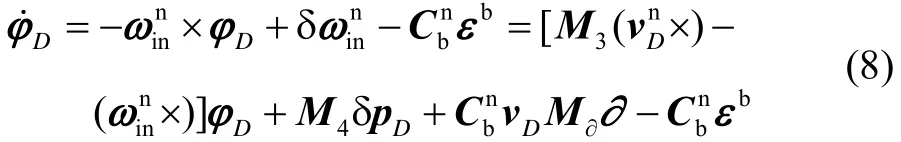
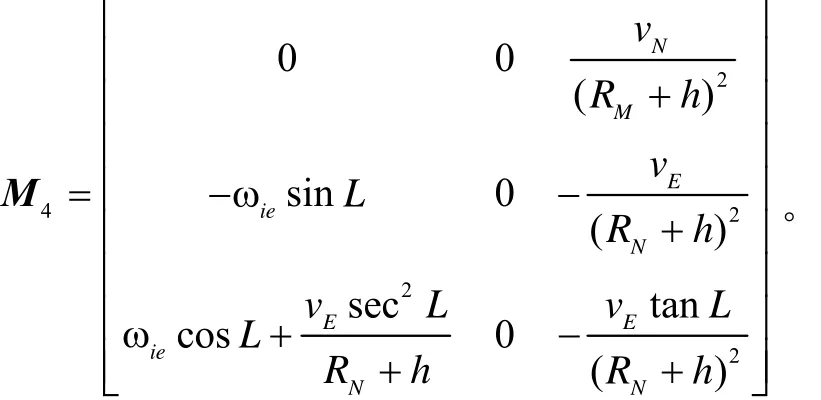
航位推算组合导航速度误差方程为

航位推算组合导航位置误差方程见式(7)。

选取状态变量为

则系统状态方程为

式中：W为系统噪声阵；

量测方程为

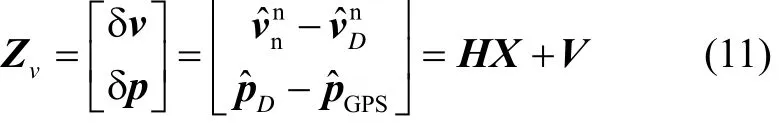
式中：v为量测噪声阵，

3 试验验证

3.1 仿真试验

设载车初始位置为东经108°，北纬34°，高度480 m；初始姿态角为[0°, 0°, 0°]，姿态误差角φD=[100″, 200″, 300″]；里程计安装俯仰角误差为0.01°，里程计安装横滚角误差为0.02°，里程计安装航向角误差为0.04°，里程计标度因数误差为误差为2‰；捷联惯导系统的陀螺常值漂移为0.1 (°)/h，加速度计零偏位1×10-4g；GPS定位精度为10 m。航位推算组合导航为600 s，载车先向北以匀加速度2 m/s2进行10 s加速，然后以20 m/s向北进行匀速行驶300 s，再绕天轴以10 (°)/s的角速度匀速进行90°转弯，接着匀速行驶直至仿真结束。

图1是航位推算组合导航系统运动轨迹图，A为起始点，B为终止点，其中点画线为航位推算运动轨迹，实线为仿真运动轨迹，载车的运动分为均加速、匀速、转弯等。图2为航位推算组合导航系统误差参数估计曲线。从图2可以看出，安装俯仰角和标度因数误差能得到有效估计，且滤波收敛时间较短。转弯前里程计安装航向角误差较大，转弯后里程计安装航向角误差估计效果得到了明显改善，取得了较高的估计精度。这主要是由于在航位推算组合导航中φD+aφ引起的误差在水平面上且垂直于载车位移方向，aθ引起的是高度方向上的误差，δKD导致沿着载车位移方向的误差，因此在航位推算组合导航经过转弯后φD的估计效果得到明显改善，相应的aφ的估计精度也提高了[3]。

图1 航位推算组合导航系统运动轨迹Fig.1 Trajectories of integrated vehicular navigation system

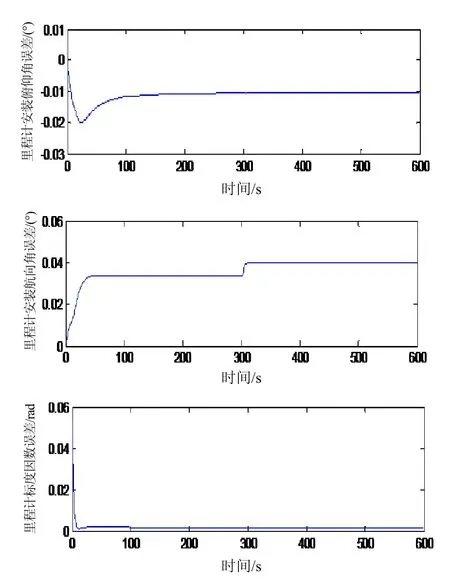
图2 航位推算组合导航系统误差参数估计曲线Fig.2 Parameter estimates of integrated vehicular navigation system

3.2 车载试验

为了验证本文提出的航位推算组合导航系统在线标定方法的有效性，利用激光捷联惯性导航系统与试验车上的里程计构成一个航位推算组合导航系统，另外利用GPS提供的量测信息作为位置参考量，对航位推算组合导航系统误差参数进行了在线标定验证。试验中陀螺精度为0.003 (°)/h，加速度计精度为5×10-5g，GPS定位精度为10 m，里程计精度为2‰D（D为里程）。利用传统里程计标定方法结果为刻度因数为23.13^/s，安装偏航角为0.168°，安装俯仰角为0.455°。在车载试验中，初始装订里程计刻度因数23.13^/s，安装偏航角为0，安装俯仰角为0。图3是车载试验跑车路线图，图4是车载试验误差参数在线标定曲线。

图3 车载试验跑车路线图Fig.3 Path graph of vehicular experiment

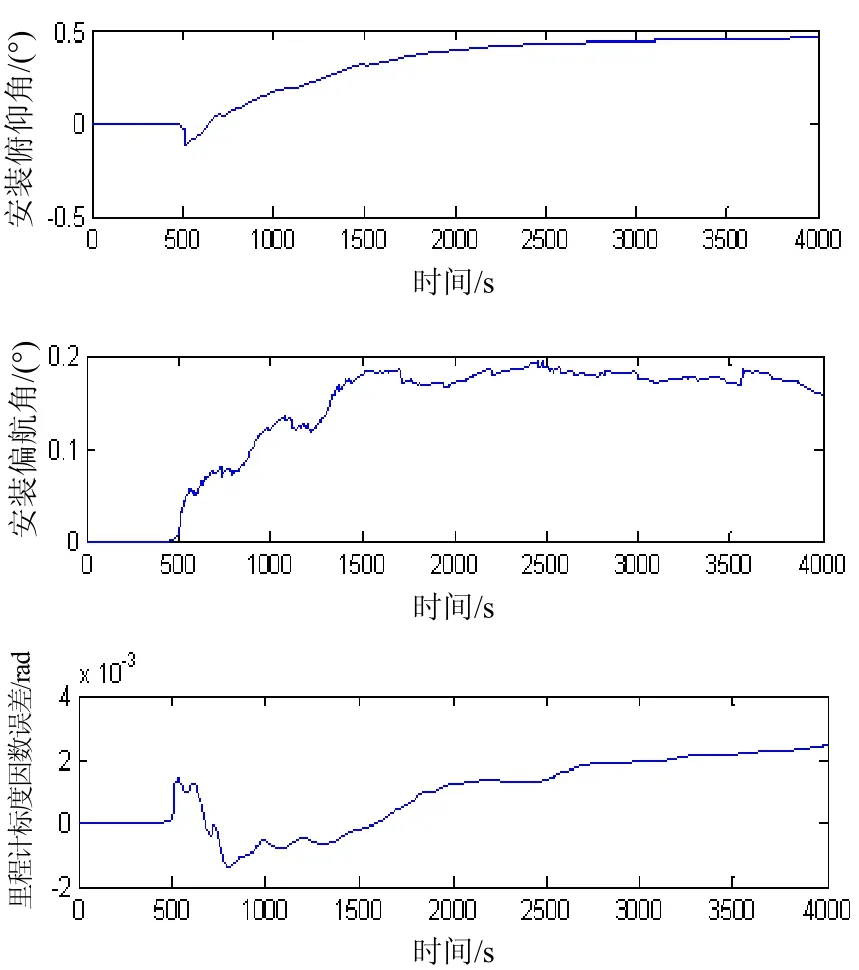
图4 车载试验在线标定曲线Fig.4 Online calibration results of vehicular experiment

从图4可以看出：通过车载试验在线标定出的里程计各误差参数与里程计传统标定法标定的结果接近；收敛时，安装俯仰角为0.46°，安装偏航角约为0.17°，刻度因数误差约为0.002。

4 结 论

仿真试验和车载试验结果表明，该算法能有效地估计里程计安装俯仰角误差、安装航向角误差和里程计标度因数。这种算法对试验环境条件要求简单，对行驶路面状况没有限制，载车运动也不受直线行驶的限制，且该算法计算量小，具有一定的工程实用价值。

（References）：

[1] 朱立彬, 王玮. 轮胎充气温度对光电里程仪标度因数影响的标定算法[J]. 中国惯性技术学报, 2011, 19(2): 190-193. Zhu Li-bin, Wang Wei. Calibration of optical odometer’s scale factor with tire inflation temperature[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 190-193.

[2] 李旦, 秦永元, 张金亮, 等. 车载惯导航位推算组合导航系统误差补偿研究[J].计算机测量与控制, 2011, 19(2): 389-391. Li Da, Qin Yong-yuan, Zhang Jin-liang, et al. Research on error compensation of integrated vehicular navigation system[J]. Computer Measurement & Control, 2011, 19(2): 389-391.

[3] 白亮, 秦永元, 严恭敏, 等. 车载航位推算组合导航算法研究[J]. 计算机测量与控制, 2010, 18(10): 2379-2381. Bai Liang, Qin Yong-yuan, Yan Gong-min, et al. On integrated navigation for vehicle dead reckoning[J]. Computer Measurement & Control, 2010, 18(10): 2379-2381.

[4] 付强文, 秦永元. INS/Doppler组合导航中安装偏角的在线估计[J]. 中国惯性技术学报, 2011, 19(2): 220-223. Fu Qiang-wen, Qin Yong-yuan. Calibration of installation error in INS/Doppler integrated navigation[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 220-223.

[5] 严恭敏. 车载自主定位定向系统研究[D]. 西安: 西北工业大学, 2006.

[6] Wang W, Wang D. Land vehicle navigation using Odometry/ INS/Vision integrated system[C]//IEEE Conference on Cybernetics and Intelligent Systems. Chengdu, China, 2008: 754-759.

[7] Wang J T, Lyle K H. Simulating space capsule water landing with explicit finite element method[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Honolulu, Hawaii, 2007(4): 23-26.

[8] Gao J, Petovello M G, Cannon M E, et al. Development of precise GPS/INS/Wheel speed sensor/yaw rate sensor integrated vehicular positioning system[C]//National Technical Meeting of the Institute of Navigation. Monterey, CA, 2006: 780-792.

[9] Obradovic D, Lenz H, Schupfner M, et al. Fusion of sensor data in Siemens car navigation system[J]. IEEE Transactions on Vehicular Technology, 2007, 56(1): 43-50.

[10] Guo Zhen, Sun Feng. Research on integrated navigation method for AUV[J]. Journal of Marine Science and Application, 2005, 4(2): 34-38.

[11] Hao Yan-ling, Liu Zhi-ping. Analysis and compensation on static error of accelerometer in GFSINS[C]//2009 International Conference on Measuring Technology and Mechatronics Automation. Hunan: IEEE, 2009: 429-43.

[12] Fong W T, Ong S K, Nee A Y C, et al. Methods for in-field user calibration of an inertial measurement unit without external equipment[J]. Measurement Science and Technology, 2008, 19(8): 1-11.

Online calibration technique for integrated vehicular navigation system

LIU Yong-hong1, LIU Ming-yong1, XIE Bo2
(1. Department of Navigation, Northwestern Polytechnical University, Xi’an 710072, China; 2. The 16thInstitute, China Aerospace Science and Technology Corporation, Xi’an 710100, China)

In view of the odometer’s installation error and scale factor error in an integrated GPS/DR vehicular navigation system, the influences of these errors on the velocity and position of dead reckoning are derived, and a new online calibration algorithm for the integrated system is put forward. In this algorithm, the velocity error between dead reckoning and GPS is used as velocity information, while the position error between dead reckoning and DGPS is used as position information. Based on this, the odometer’s attitude error, installation error and scale factor error are estimated. The effectiveness of the algorithm is validated by simulation and vehicular experiments, which show that the online-calibrated error parameters by this algorithm have similar results with those by traditional calibration method, and the algorithm has less calculation amount, showing that it has certain engineering application value.

dead reckoning; integrated navigation; installation error; scale factor

U666.1

A

1005-6734(2015)04-0434-04

10.13695/j.cnki.12-1222/o3.2015.04.003

2015-01-26；

2015-05-05

船舶预研基金（12J4.2.4）

刘永红（1981—），女，博士研究生，主要从事惯性导航器件研究。E-mail：whitebirdfly@hotmail.com

联 系 人：刘明雍（1971—），男，教授，博士生导师。E-mail：liumingyong@nwpu.edu.cn