双质量硅微机械陀螺仪正交校正系统设计及测试

曹慧亮，李宏生，申 冲，石云波，刘 俊，杨 波

（1. 中北大学 仪器科学与动态测试教育部重点实验室，太原 030051；2. 中北大学 电子测试技术国防科技重点实验室，太原 030051；3. 东南大学 仪器科学与工程学院，南京 210096）

双质量硅微机械陀螺仪正交校正系统设计及测试

曹慧亮1,2，李宏生3，申 冲1,2，石云波1,2，刘 俊1,2，杨 波3

（1. 中北大学 仪器科学与动态测试教育部重点实验室，太原 030051；2. 中北大学 电子测试技术国防科技重点实验室，太原 030051；3. 东南大学 仪器科学与工程学院，南京 210096）

为了减小正交误差对双质量硅微机械陀螺仪性能的影响，进一步提高陀螺精度和工程化成品率，对双质量结构正交耦合刚度校正法进行了研究。首先，针对双质量陀螺结构的特殊形式，分析了其左、右结构中正交耦合刚度不相等的原因，并结合相敏检测相位误差对正交耦合刚度值进行了计算，进一步量化了其对输出信号的影响；其次，结合正交校正梳齿结构介绍了耦合刚度校正法的工作原理，并基于左、右结构单独校正的方法设计了双质量结构正交校正控制系统；最后，对正交校正前后的双质量微机械陀螺仪进行了详细测试，结果证实了双质量单独校正比整体校正效果更好，各项参数均有较大提高，其中零偏稳定性从校正前的540 (°)/h提高到了正交后的24.05 (°)/h（1σ），证明了提出的两质量块单独校正方法的可行性和实用性。

双质量硅微机械陀螺仪；正交误差；正交耦合刚度校正；两质量块单独校正；性能测试

硅微机械陀螺仪的设计和加工技术在近几年中有了很大进步，使其应用领域进一步拓展，除了满足传统的汽车安全、消费电子、机器人等领域之外[1]，一些精度要求比较高的领域也逐渐出现了硅微机械陀螺仪，比如应用在Micro PNT（基于微系统技术的定位、导航、授时技术）中的微机械陀螺仪精度需求为零偏稳定性0.01 (°)/h，而目前美国已经研发的微机械陀螺的零偏稳定性已经达到了0.05 (°)/h（Allan方差计算）[2]。国内外大多数研究机构提出的高精度微机械陀螺仪都采用了双质量音叉振动形式[3]-[6]，其特点为左右质量块可组成统一的驱动模态，不仅避免了由于加工误差产生的两质量块不对称造成的驱动频率不一致，而且使得检测模态也工作在反相运动状态以减小检测轴方向共模误差影响，如检测轴方向的加速度输入。

在硅微机械陀螺仪的工程化过程中，在硅结构加工过程中产生的正交误差是影响陀螺精度的主要因素之一[7-8]。而通常情况下，加工误差在左、右质量块上产生正交误差往往不同，所以正交误差对双质量结构振动特性方面的影响需要进一步详细分析。同时，在上述基础上设计的正交校正控制系统也应进行特殊设计。因此，对双质量陀螺正交校正系统的设计和分析可在现有加工工艺基础上进一步提高陀螺精度，有很强的现实意义。带有正交校正梳齿的双质量硅微机械陀螺仪的结构示意图如图1所示[9]。

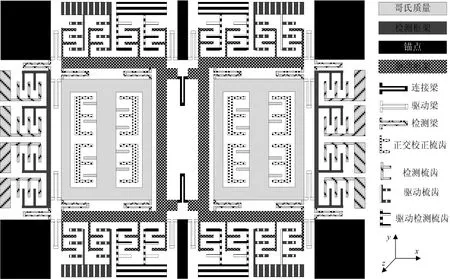
图1 带有正交校正梳齿的双质量全解耦陀螺结构示意图Fig.1 Schematic of dual-mass fully decoupled gyroscope structure with quadrature error correction combs

1 双质量陀螺结构的正交误差

正交误差产生的原因为加工误差引起的不等弹性，其会引起检测框架和质量块的正交运动，该运动的频率等于驱动模态谐振频率，相位与哥氏信号相差90°。所以，正交误差与系统的刚度矩阵密切相关。

在理想微机械陀螺的基础上加入正交误差耦合刚度和耦合阻尼等非理想因素后可得陀螺的动力学方程可描述为

式中：mx和my分别是驱动和检测模态等效质量；cxx、cyy和kxx、kyy分别是驱动和检测模态的有效阻尼和刚度；cxy和kxy和kyx是检测模态耦合到驱动模态的刚度和驱动模态耦合到检测模态的刚度；Fdx=Fdsin(ωdt)为驱动力；mp为哥氏质量；Ωz为绕z轴输入的角速率；x和y为驱动和检测方向的位移。由于采用了闭环自激振荡技术，所以驱动力的频率应与驱动模态谐振频率相等，即有ωd=ωx=(kxx/mx)0.5。进一步，可设驱动位移x=Axcos(ωdt)。

将图1中的质量和刚度模型进行简化可得图2，该图为理想状态的刚度系统，左右刚度系统通过“连接梁等效弹簧”进行耦合。由于该弹簧实际是由U型梁形成，理想状态下，虽然该结构在y轴方向具有较大刚度，但加工误差可使U梁两固定端连线不与x轴平行，则会导致其刚度矩阵扭转，一方面使沿x轴方向刚度产生一定变化，另一方面在左、右结构之间起到了一定的应力隔绝作用。

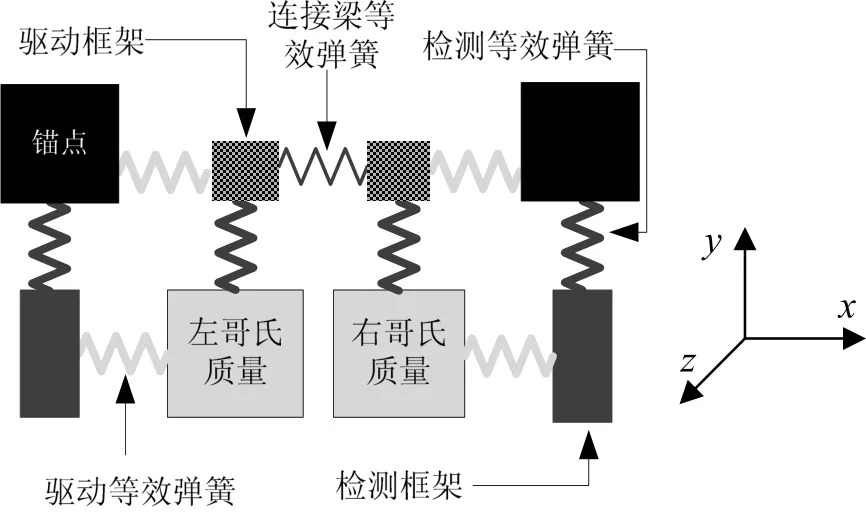
图2 双质量等效刚度系统示意图Fig.2 Schematic of dual-mass structure stiffness system

将简化图2中左侧检测框架、左侧驱动框架和左侧哥式质量以及它们之间的连接弹簧看作一个整体“左结构”，同理可得“右结构”，两结构之间通过 “连接梁等效弹簧”连接，在存在加工误差的情况下整个系统如图3所示。由于加工误差对于任何结构形式的影响具有很强的随机性，即使是同一结构的左右质量块中的误差也无法做到完全一致，所以左、右结构产生的正交误差角（图3中β）很难相等，甚至会反相。因此，对于左右质量块需要进行单独校正以消除各自的加工误差的影响。通常情况下，由于U型梁两个长梁臂尺寸相等且驱动模态条件下两个质量块向相反方向振动，所以连接梁中点位置不会随梁臂运动。为了简化分析过程，本文以单（右）质量为例进行分析，将连接梁两个梁臂分别划分至左右两个结构的振动系统中。通过投影法可得右侧结构中krx和kry在x和y轴上的实际作用力为

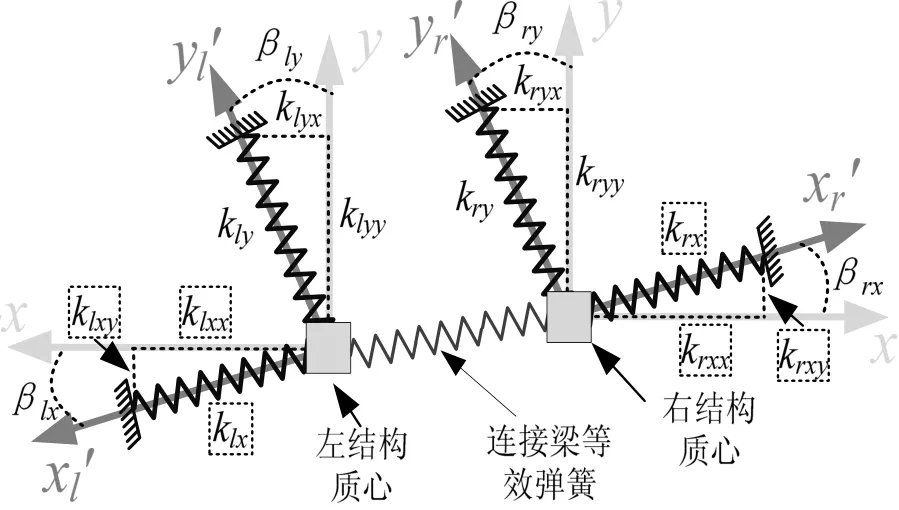
图3 加工误差影响下的双质量-弹簧系统示意图Fig.3 Dual-mass spring system with manufacture error

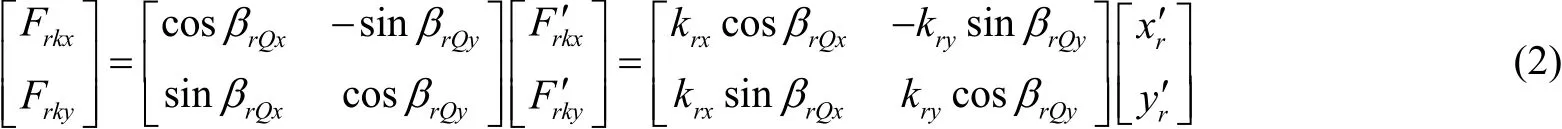
式中：Frkx和Frky分别是右结构沿理想驱动轴（x轴）和检测轴（y轴）的弹性力；βrQx和βrQx分别为右结构的弹性主轴在驱动方向和检测方向的正交误差角；F’rkx和F’rky分别是沿实际驱动轴（x′轴）和检测轴（y′轴）的弹性力；krx、kry分别是驱动和检测轴总刚度（包含由连接梁产生的刚度）；xr′和yr′分别是右结构沿x′轴和y′轴的位移。经坐标变换后有

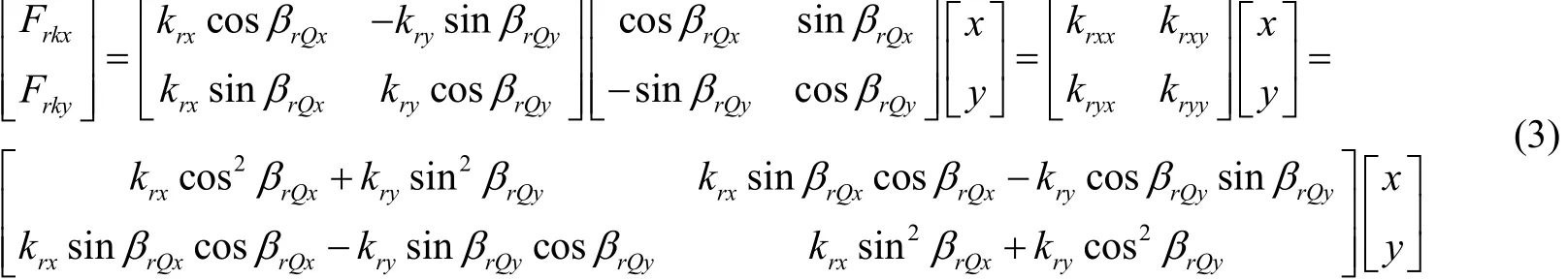
从式(3)可得式(1)中对于右结构的刚度矩阵的各元素为

从式(4)可知，存在kryx=krxy，这两个耦合刚度是正交误差在陀螺力学模型中的表现形式，但是驱动幅度远大于检测幅度，所以驱动对检测的正交耦合力较大，而检测到驱动模态的耦合力由于远小于驱动力而可被忽略。将式(4)的值带入式(1)可得正交误差等效输入角速率：

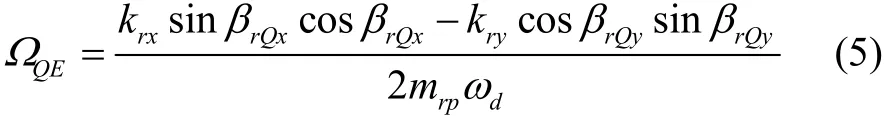
式中，mrp为右结构哥氏质量。由于系统检测回路采用了相敏解调方案，所以陀螺输出中存在哥氏同相信号（如耦合阻尼），令同相信号的等效输入角速率为定值ΩIP=5 (°)/s，取正交信号为变量且设ΩQE＜200 (°)/s，解调相角误差和噪声φd,error+φd,noise在-2°到2°之间。绘制陀螺输出信号中同相分量和正交分量的等效角速度ΩO如图4所示，可以看出，解调相角变化范围内的同相信号对应的ΩO只变化了0.003 (°)/s，而正交误差分量随着解调相角变化的比较剧烈，ΩO变化了近15 (°)/s。所以，正交误差对输出信号影响很大，抑制正交误差是提高陀螺性能的有效途径之一。

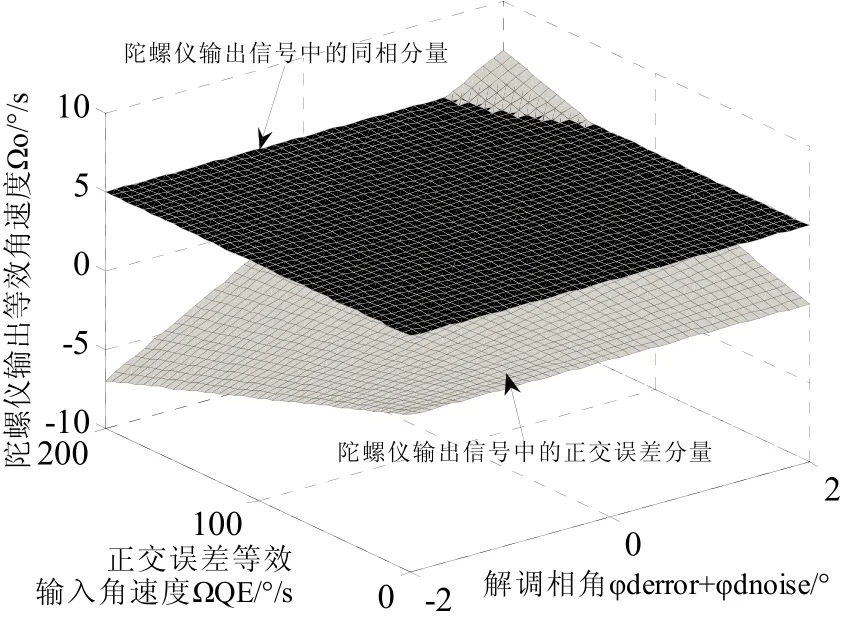
图4 陀螺输出信号中的同相和正交分量幅值Fig.4 Amplitude of in-phase and quadrature error components in gyroscope output signal

2 双质量陀螺结构的正交耦合刚度校正

由于产生正交误差的根源为正交耦合刚度，所以直接对正交耦合刚度进行校正的效果应优于对正交误差信号或正交力的校正。本文利用不等间距梳齿对正交耦合刚度进行校正，其结构如图5所示。

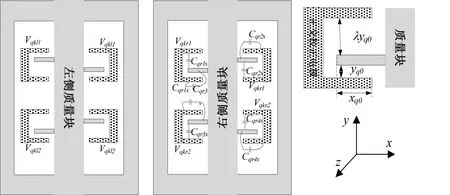
图5 正交校正梳齿电极示意图Fig.5 Schematic of quadrature error correction combs

首先标记右质量块与四个固定电极交叠的8个电容（由于梳齿顶端面积较小，梳齿顶-底间距较大，故忽略梳齿顶-底间的电容），左上和左下电极、右上和右下电极分别由基底上的引线连通，并在质量块和这两组电极间施加电压Vqkr1和Vqkr2。当质量块向驱动轴和检测轴方向有位移x和y时，则上述电容可用矩阵形式表达：

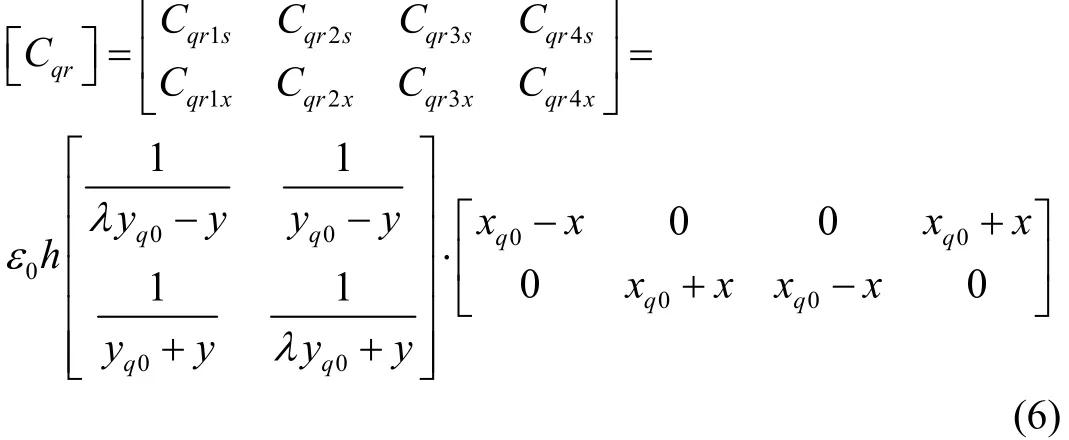
式中，ε0为介电常数，h为结构高度。根据平行板电容器产生静电力的原理，可得到沿x方向和x方向的施力矩阵：

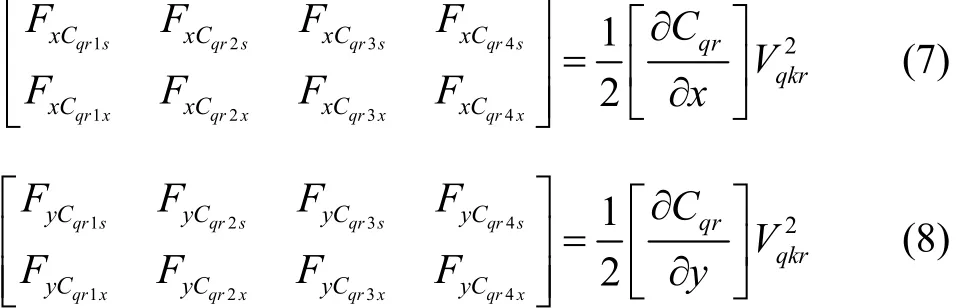
将式(6)代入上述两式，并将结果中各元素求矢量和可得静电力合力：

式中，nq为梳齿个数。在上述两式的左右两边分别对x和y求偏导后可得到这两个力在驱动和检测轴的刚度矩阵如下式所示：

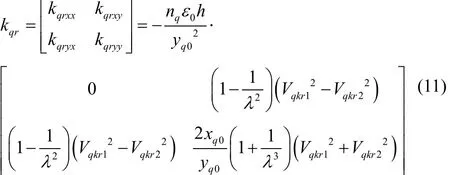
该式为正交校正梳齿可产生的静电刚度，该刚度矩阵与式(3)中刚度矩阵叠加后为模态的实际刚度矩阵。所以，若取kqryx=-kryx，则正交耦合刚度可被完全校正。同时，应考虑kqryy项对检测模态谐振频率的影响，经实验验证该影响小于检测频率的1%。由于正交校正对驱动模态等效刚度无直接影响，而开环状态下系统的标度因数与驱动-检测频差相关，所以正交校正后系统的标度因数会发生一定变化。

本文基于正交刚度耦合校正法的双质量硅微陀螺仪正交校正系统如图6所示。系统采用了左、右质量块单独校正的方式，采用PI控制器，相关参数根据左、右结构中的正交耦合刚度不同而各自设计。由于两质量块的驱动模态振动频率相同，所以相敏解调模块采用了相同的基准信号cos(ωdt+φ)。图6中，GlSV/F和GrSV/F分别为左、右结构的传递函数，Vref=0 V为控制基准，FlLPF和FrLPF分别为低通滤波器，Klk和Krk为电压-刚度转换传递函数。

整个系统的控制对象为正交耦合刚度klyx和kryx：通过相敏检测方法检测回路中的正交信号，提取其幅值后与参考基准进行比较，将比较结果送至PI控制器产生控制信号Vlkl1和Vlkr1，控制信号与固定的电压信号Vlkl2和Vlkr2一起产生静电负刚度kqlyx和kqryx，它们分别与原耦合刚度klyx和kryx叠加后形成新的耦合刚度，再次进入控制回路，如此循环，直至正交误差信号幅度与Vref相等。

3 实 验

根据上文中提出的控制系统，在PCB板上搭建了实际的测控系统，如图7所示。为了体现和验证本文所述方法的正确性，首先对质量块输出的正交信号进行测试，在未加入任何正交校正时，左、右质量块的输出如图8所示，图中四条曲线从上而下分别为驱动位移信号，左质量块输出信号，右质量块输出信号，两质量块输出信号之和。

图7 陀螺仪实物照片Fig.7 Gyroscope photo

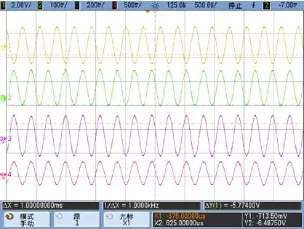
图8 正交校正前信号Fig.8 Quadrature error signals

图8中驱动位移信号峰峰值约为3 V，左、右质量块输出信号幅值分别约为150 mV和300 mV，两信号虽然相位相同（与驱动位移信号同相，为正交信号），但幅值差别较大，这验证了本文在第一节中提出的左右结构正交误差不等的内容。第四条曲线为两质量块输出信号之和，峰峰值约为450 mV。在目前的双质量结构正交校正相关论文中，控制方法采用的是双质量整体校正，即以两质量块输出信号之和为控制对象，对左右质量块正交校正梳齿施加同样的控制信号。本文在整体校正的基础上进行了实验，曲线如图9所示。

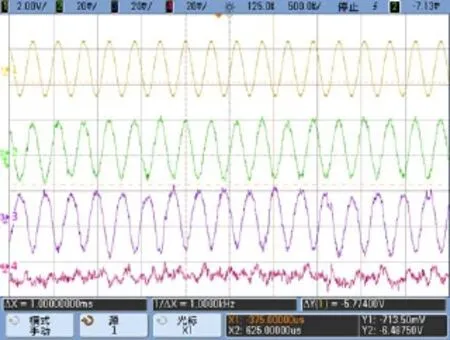
图9 双质量整体校正曲线Fig.9 Total correction signals for quadrature errors

图9中最上方曲线为驱动位移信号，峰峰值约为3 V；第二和第三条曲线为左、右质量块输出信号，幅值大致相等，均为40 mV，两信号相位相反，与驱动位移信号保持同（反）相，仍为正交信号；第四条曲线为陀螺整体输出信号，几乎没有正交信号的痕迹，只是噪声信号。通过二、三条曲线可知，左质量块的正交信号未完全消除（欠校正状态），而右质量块处于过校正状态。图10为本文提出的两质量块各自校正方法实验，图中第一条曲线为驱动位移信号，第二和第三条依然为左、右质量块输出信号，从中可看出，两质量块输出信号已经没有了正交信号，只是噪声信号，两质量块的正交耦合刚度同时得到了有效校正，结果优于先前的整体校正。

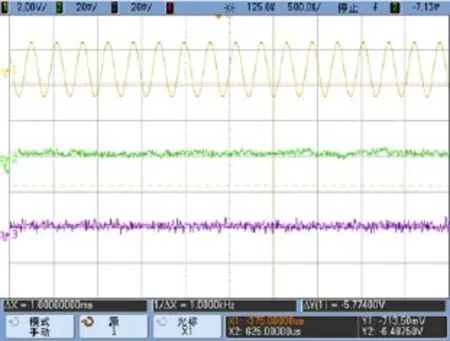
图10 双质量独立校正曲线Fig.10 Separate correction signals for quadrature errors

在双质量独立校正的基础上，对微机械陀螺仪正交校正前后的特性进行整机测试，包括零偏常温和全温，标度因数的常温和全温。标度因数和零偏常温测试如图11和图12所示，零偏全温测试曲线如图13（前半部分为从+60℃降温至-40℃曲线，后后半部分为从-40℃到+60℃升温曲线）。测试结果如表1所示。

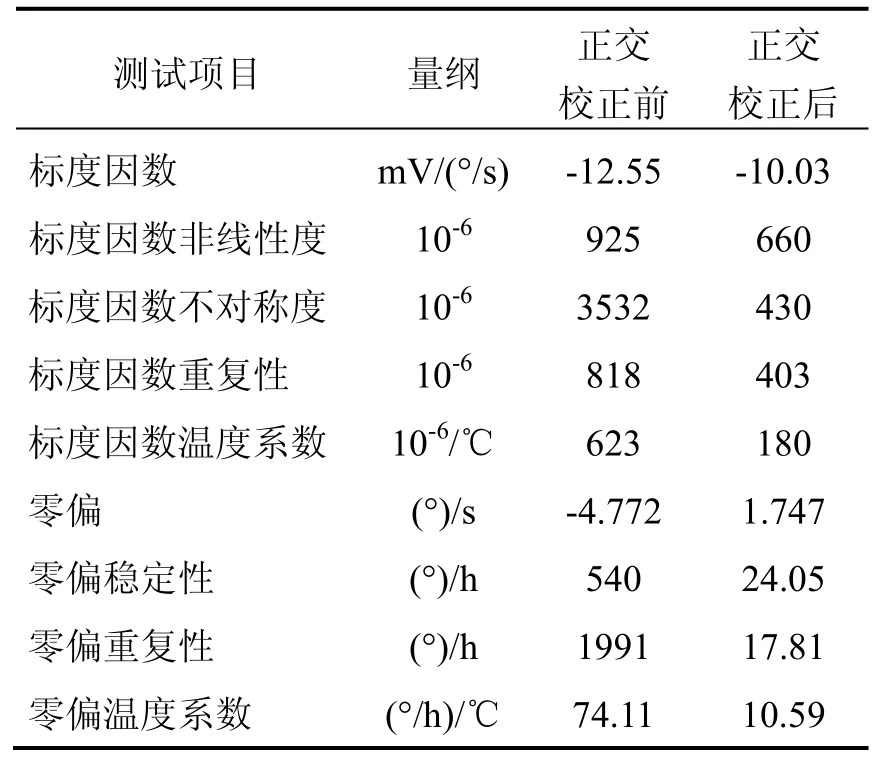
表1 测试结果Tab.1 Testing results of the gyroscope

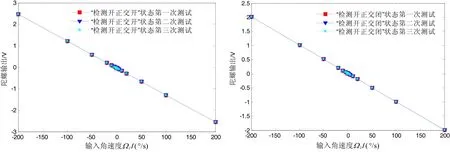
图11 正交校正前（左）、后（右）标度因数常温测试曲线Fig.11 Scale factor’s ordinary temperature testing curves before and after quadrature error correction

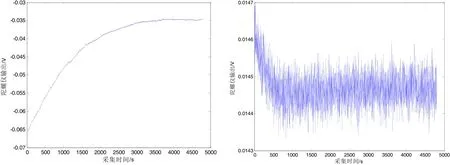
图12 正交校正前（左）、后（右）零偏常温测试曲线Fig.12 Bias’s ordinary temperature testing curves before and after quadrature error correction

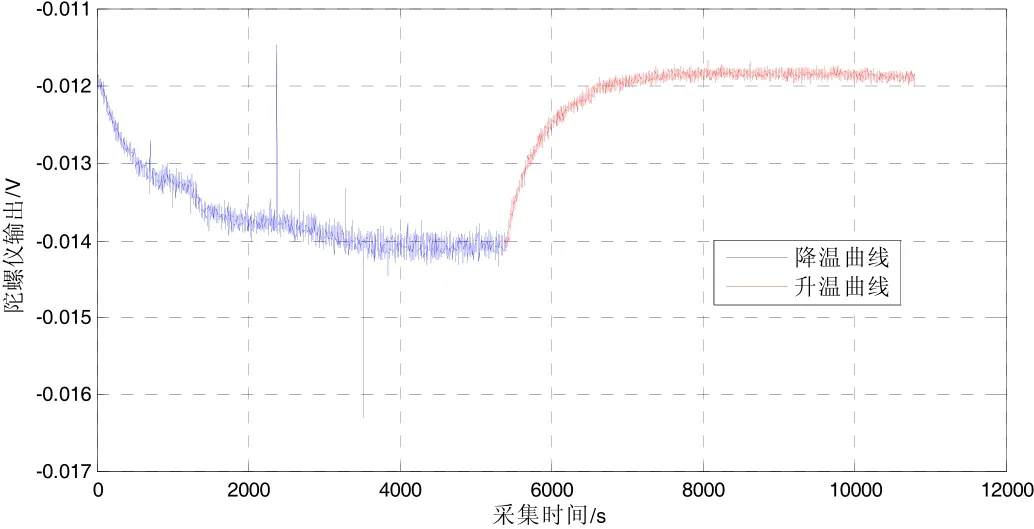
图13 正交校正后零偏全温测试曲线Fig.13 Bias’s whole temperature testing curve after quadrature error correction

4 结 论

双质量硅微机械陀螺仪的正交误差是限制其精度进一步提高的主要因素，本文针对正交耦合刚度提出了双质量各自单独正交校正方案，并设计了相应的正交校正系统，通过实验证明了该方案相对于双质量整体校正方案的优势。在此基础上对双质量硅微机械陀螺仪整机进行了常温和全温的测试，结果显示正交校正后陀螺的各项性能均有较大改善，证明了本文提出的正交校正系统的可行性，为双质量微机械陀螺仪的正交校正提供了更优方案。

（References）：

[1] 曹慧亮, 李宏生, 王寿荣, 杨波, 黄丽斌. MEMS陀螺仪结构模型及系统仿真[J]. 中国惯性技术学报, 2013, 21(4): 524-529. Cao Hui-liang, Li Hong-sheng, Wang Shou-rong, Yang Bo, Huang Li-bin. Structure model and system simulation of MEMS gyroscope[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 524-529.

[2] Shkel A M. Precision navigation and timing enabled by microtechnology: Are we there yet?[C]//Proc SPIE Int Soc Opt Eng Micro- and Nanotechnology Sensors, Systems, and Applications III. 2011, vol.8031: 18.1-18.9.

[3] Erdinc T, Said E A, Tayfun A. Quadrature-error compensation and corresponding effects on the performance of fully decoupled MEMS gyroscopes[J]. Journal of Micro-Electromechanical Systems, 2012, 21(3): 656-667.

[4] Chaumet B, et al. A new silicon tuning fork gyroscope for aerospace applications[C]//Symposium Gyro Technology. 2009: 1.1- 1.13.

[5] Lapadatu D, Blixhavn B, Holm R, et al. SAR500 - a high-precision highstability butterfly gyroscope with north seeking capability[C]//IEEE/ION Position Location and Navigation Symposium. 2010: 6-13.

[6] Zaman M F, Sharma A, Hao zhili, et al. A mode-matched silicon-yaw tuningfork gyroscope with subdegree-perhour Allan deviation bias instability[J]. Journal of Microelectromechanical Systems, 2008, 17(6): 1526-1536.

[7] 王晓雷, 杨成, 李宏生. 硅微陀螺仪正交误差校正系统的分析与设计[J].中国惯性技术学报, 2013, 21(6): 822-827. Wang Xiao-lei, Yang Cheng, Li Hongsheng. Analysis and design of quadrature error correction system for silicon micro-gyroscopes[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 822- 827.

[8] Su Jian-bin, Xiao Dong-bang, Chen Zhihua, et al. Improvement of bias stability for a micromachined gyroscope based on dynamic electrical balancing of coupling stiffness[J]. J. Micro/Nanolith MEMS MOEMS, 2013, 12(3): 033008.

[9] 倪云舫, 李宏生, 杨波, 等. 硅微陀螺正交误差直流校正设计与分析[J]. 中国惯性技术学, 2014, 22(1): 104-108. Ni Yun-fang, Li Hong-sheng, Yang Bo, et al. Design and analysis of a quadrature correction method sing DC voltages for silicon micro-gyroscope[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 104-108.

[10] Cao Hui-liang, Li Hong-sheng. Investigation of a vacuum packaged MEMS gyroscope architecture’s temperature robustness[J]. International Journal of Applied Electromagnetics and Mechanics, 2013(41): 495-506.

[11] 罗兵, 张辉, 吴美平. 硅微陀螺正交误差及其对信号检测的影响[J]. 中国惯性技术学报, 2009, 17(5): 604-607. Luo Bing, Zhang Hui, Wu Mei-ping. Quadrature signal of microgyroscope and its effect on signal detection[J]. Journal of Chinese Inertial Technology, 2009, 17(5): 604-607.

Design and test on quadrature error correction system of dual-mass silicon MEMS gyroscope

CAO Hui-liang1,2, LI Hong-sheng3, SHEN Chong1,2, SHI Yun-bo1,2, LIU Jun1,2, YANG Bo3
(1. Key Laboratory of Instrumentation Science and Dynamic Measurement Ministry of Education, North University of China, Taiyuan 030051, China; 2. Key Laboratory of Science and Technology on Electronic Test & Measurement, North University of China, Taiyuan 030051, China; 3. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)

The quadrature-coupling stiffness correction method for dual-mass silicon MEMS gyroscope is investigated to reduce the quadrature error’s influence and improve the gyro’s precision and the finished product rate. Firstly, the unequal reason of the left and right masses’s coupling stiffness is analyzed based on the dual-mass structure, and the quadrature stiffness value is calculated taking into account the phase sensitivity demodulation error which contributes great error and drift to the gyro output. Secondly, a quadrature error correction comb is introduced, and a two-mass quadrature error separate compensation system is proposed. Finally, experiments are conducted to test the gyro performance, which show that the separate correction method has better result compared with the integral correction method, and the parameters are significantly improved after quadrature error correction, in which the bias stability is increased to 24.05 (°)/h (1σ) from 540 (°)/h, verifying the feasibility and practicality of the proposed method.

dual-mess MEMS gyroscope; quadrature error; coupling stiffness correction; two mass separate correction; performance test

U666.1

A

1005-6734(2015)04-0544-06

10.13695/j.cnki.12-1222/o3.2015.04.023

2015-04-15；

2015-07-28

总装预研基金项目（9140A09011313JW06119）；江苏省科技攻关项目（BE2014003-3）；国家杰出青年科学基金（51225504）；国防973（2012CB723404）；国家自然科学基金委员会和中国工程物理研究院联合基金资助（U1230114）；中北大学校基金

曹慧亮（1986—），男，博士，讲师，从事微机械系统方面研究。E-mail：caohuiliang@nuc.edu.cn