基于地球红外辐射场的旋转弹丸姿态测试方法

于 靖，卜雄洙，杨 波，王新征

（南京理工大学 机械工程学院，南京 210094）

基于地球红外辐射场的旋转弹丸姿态测试方法

于 靖，卜雄洙，杨 波，王新征

（南京理工大学 机械工程学院，南京 210094）

针对微惯性器件无法满足高转速弹丸飞行过程中的滚转姿态测量要求的问题, 提出了基于地球红外辐射场的旋转弹丸姿态测试方法。首先，研究了地球红外辐射场的产生机理和特性，分析了天地间红外辐射率的变化规律。然后，结合旋转弹丸在飞行过程中的运动特征，建立了红外传感器测量模型，推导了弹丸姿态与传感器感测信号的函数关系。最后，合理布局红外传感器，基于误差传递的原理，改进了常规的姿态解算算法，进一步提高了传感器测试信号的利用率。结果表明，利用地球红外辐射场测姿具有较高的精度，俯仰角解算误差在±0.3°以内，改进解算方案的横滚角解算误差在±0.5°以内。该姿态测量系统简单有效，能够满足旋转飞行体的姿态测量要求。

旋转弹丸；地球红外辐射场；误差分析；姿态解算

随着对弹药射击精度要求的提高及各种子母弹和灵巧弹的研制，需要掌握弹丸飞行的规律，精确测量弹丸的各种实际飞行参数成了制导的关键，因此迫切要求测试弹丸的飞行姿态参数[1]。地球的红外辐射特性对于军事国防、气象预报和农业等领域具有十分重要的意义[2]。近年来，地球红外辐射特性的研究受到了越来越多的关注。

目前国内外所从事的利用地球红外辐射场姿态角测试研究工作大多局限于卫星、飞机等大型飞行器的应用层面[3-4]，对于弹丸的姿态角测试方面的应用研究还不太充分。弹丸的实际飞行轨迹和特点与卫星、飞机的飞行特点有较大差别，尤其在弹丸进行高速旋转的状态下，地球红外辐射场的变化比起卫星、飞机来说要复杂得多[5-6]。因此，单纯利用卫星、飞机等红外姿态测试的先验知识来分析弹丸运动时的地球红外辐射场是远远不够的。要实现对弹丸姿态的高精度测量要求，必须对弹丸在飞行过程中地球红外辐射场的变化进行深入的研究分析。本文在研究地球红外辐射场理论的基础上，建立红外传感器测量模型，推导弹丸姿态与传感器信号的函数关系。根据误差传递原理，改进常规的解算方案。最终通过数值仿真对该测试方法的有效性和可行性进行验证。

1 地球红外辐射场理论

由于大气与地面热容量的不同，导致大气的温度比地面的要低，因此在天空和大地之间存在着一个红外辐射梯度场。红外传感器是基于热电堆原理研制而成，根据普朗克黑体辐射定律和维恩位移定律工作。通过感受天空和大地之间的红外辐射能量，输出一个与温度成比例关系的电压信号。由于大地的温度要远高于天空的温度，当红外传感器的感应面垂直指向天空时，输出电压最小；当其感应面垂直指向大地时，输出电压最大。因此，地球红外辐射大小与观测角度有关。

天空与大地之间的红外辐射率ε()β是关于红外传感器对地平线角度β的函数关系式[7]：

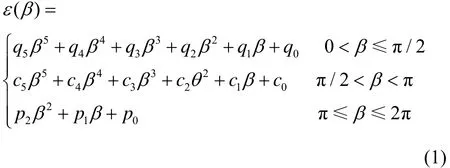
式中，qi、ci、pi是相关多项式系数，具体数值如表1所示。

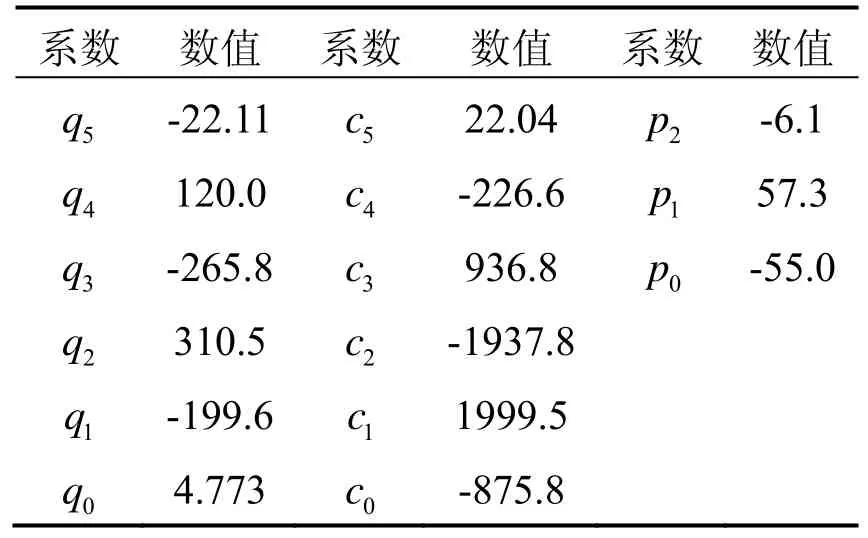
表1 多项式系数值Tab.1 Polynomial coefficient values

从式(1)中可以看出，地球红外辐射场的大小与红外传感器对地平线角度β相关，图1所示为地球红外辐射率关于β的变化关系。

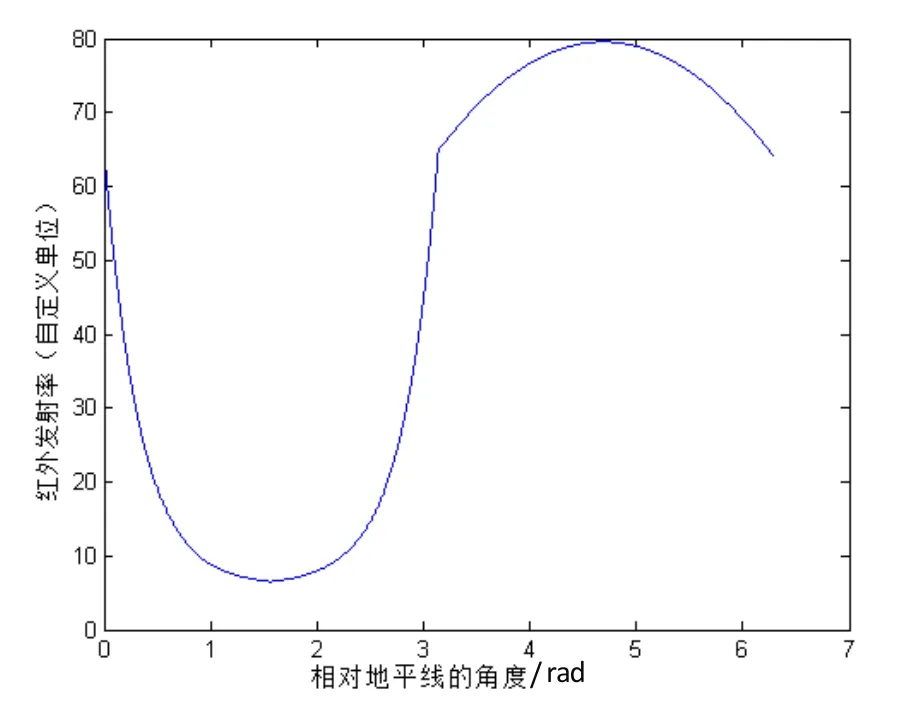
图1 红外辐射率关于β的变化示意图Fig.1 IR emissivity as a function of β

2 传感器测量模型

在弹丸侧面安装一对红外传感器，通过测量天空和地面的温差来得到红外传感器的对地倾角大小，进而可以得到弹丸的姿态角，其测量示意图如图2所示。

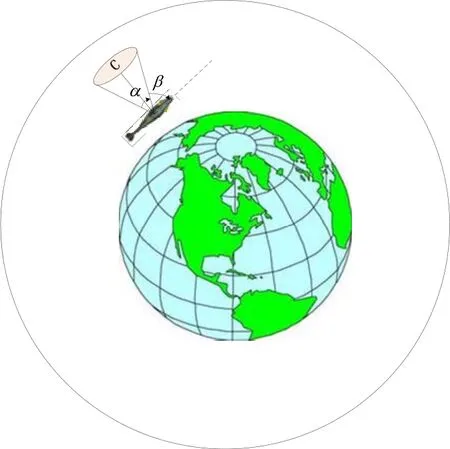
图2 弹载红外传感器测量示意图Fig.2 Schematic of infrared sensors mounted on projectile

传感器的输出电压取决于其敏感面所对应的圆锥体所截的那部分面积，如图2中圆C所示，输出电压可按照下式计算[8]：

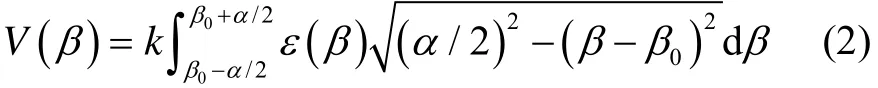
式中，V为输出电压，k为传感器系数，α为传感器的视场角，β0为红外传感器视场角平分线对地倾角。

根据红外传感器视场角α的变化范围，结合式(1)中β的取值范围，对式(2)的输出电压求解作以下的区域划分。图3所示为0＜α＜π/2时，积分求解划分的6个区域；图4所示为π/2＜α＜π时，积分求解划分的6个区域。

针对图3和图4所划分的积分求解区域，可以将红外传感器的输出电压积分求解区域按照α和0β的取值范围作如下划分，具体如表2所示。

图3 0＜α＜π/2的区域划分示意图Fig.3 Computational regions of [0,π/2]

图4 π/2＜α＜π的区域划分示意图Fig.4 Computational regions of [π/2,π]

表2 积分求解区域划分Tab.2 Computational regions of integral solving

根据式(2)可以实时计算出弹丸在旋转过程中，红外传感器的对地倾角变化，通过坐标转换矩阵，可以得出其与弹丸姿态角的关系：

式中，θ为弹丸的俯仰角，γ为弹丸的横滚角。可以看出，当θ=0°时，0β即为弹丸的横滚角。

图5 不同俯仰角下传感器输出随横滚角的变化Fig.5 Sensor output under different pitch angles

因此，在弹丸旋转过程中，弹载红外传感器将会输出一个近似正弦信号，幅值与载体的俯仰角有关，其频率与旋转飞行体旋转速率相关。通过数据分析和拟合，弹载红外传感器的测量模型如下：

式中，V为红外传感器的输出电压，B为输出信号的偏置，δ为相位角。

3 旋转弹丸姿态解算及数值仿真

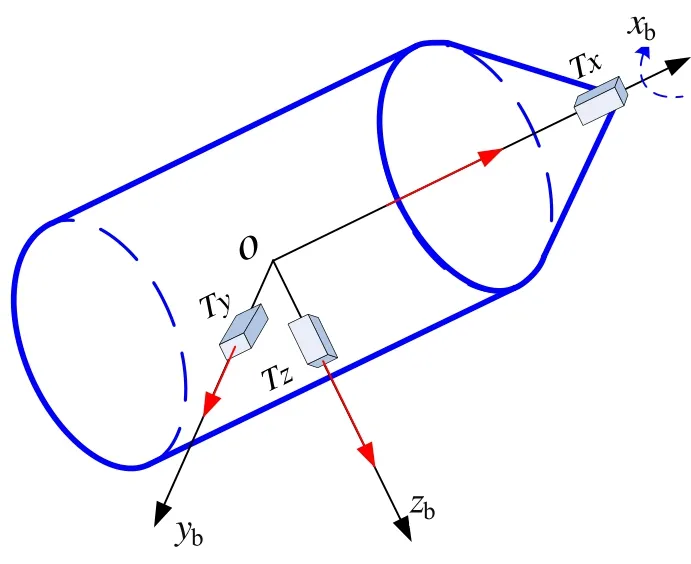
图6 红外传感器安装示意图Fig.6 Schematic of thermopiles sensors installation

3.1 红外传感器布局

设旋转弹丸的质心在弹丸坐标系O-xbybzb的原点O处，弹丸的自转轴为xb轴且指向xb轴的正方向。如图6所示，红外传感器Tx、Ty、Tz分别沿弹丸坐标系的三个坐标轴安装，其敏感轴方向均指向坐标轴的正向。

当弹丸在空间中有姿态运动时，弹丸坐标系与地理坐标系不再重合，红外传感器的测量值与该时刻下的弹丸俯仰角θ、横滚角γ有关。归一化红外传感器系数，调整偏置及相位角，三轴红外传感器输出可按照下式计算：

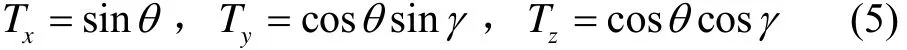
根据弹载三轴红外传感器的输出公式(5)，可以通过x轴的输出解算弹丸的俯仰角，结合其他两轴的输出解算出横滚角，从而获得弹丸的姿态信息。

3.2 改进的姿态解算方案

基于上述分析，常规解算方案是：首先x轴的输出解算弹丸的俯仰角γ，接着将解算出的俯仰角结合y轴的输出即可解算出弹丸的俯仰角θ。由于弹丸俯仰角θ的定义范围为[-90°～+90°]，横滚角γ的定义范围为[-180°～+180°]，根据z轴的输出可以判断俯仰角θ和横滚角γ所处的象限[9-10]。

然而，实际测量过程中Tx、Ty、Tz的输出都是带有误差的，根据误差传递原理可以进行如下分析。

俯仰角可以按下式解算：

横滚角可以按以下两式计算：

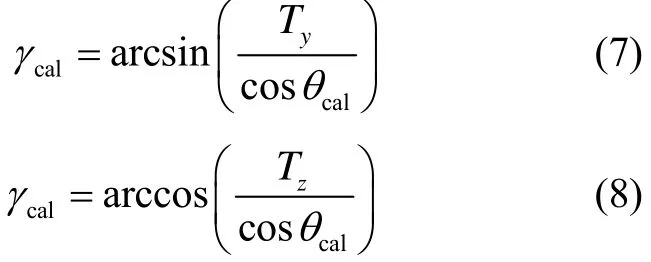
俯仰角的解算只根据一个测量因素Tx的输出确定，而横滚角的解算与多个测量因素相关，包括了Ty或Tz和俯仰角解算值，因此必须合理利用各个因素，才能使解算结果的误差为最小。

根据式(7)，函数的标准差为

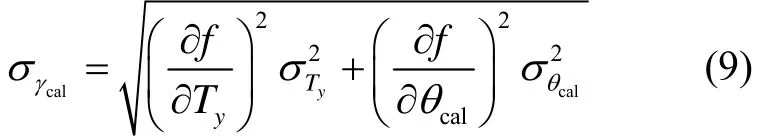
由函数误差公式可知，若使各个测量值对函数的误差传递系数为0或为最小，则函数误差可相应减小。由于θcal只能通过Tx解算，而σγcal可以通过Ty或Tz解算，因此要使Ty或Tz的误差传递系数越小越好。

由式(10)可知，Ty的绝对值越小，其误差传递系数越小，横滚角的解算误差越小。同理，Tz的绝对值越小，横滚角的解算误差越小。

因此在实际测量过程中，改进常规的解算方案，采用交替使用Ty或Tz来解算横滚角，使横滚角的解算误差尽量减小，即：当Ty≤Tz，采用Ty解算横滚角，采用Tz判断横滚角象限；当Ty＞Tz，采用Tz解算横滚角，采用Ty判断横滚角象限。

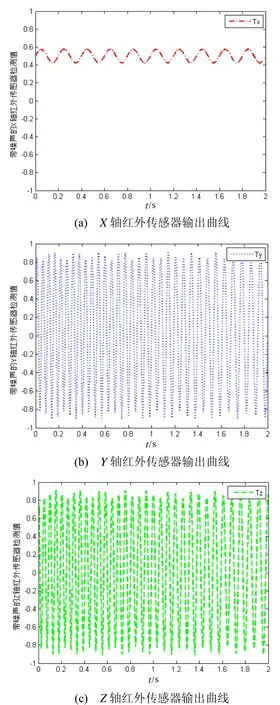
图7 弹载三轴红外传感器输出曲线Fig.7 Output of three-axis thermopiles sensors

3.3 数值仿真

根据上述基于地球红外辐射场的旋转弹丸姿态测试方法，按如下条件进行了数值仿真：俯仰角θ在30°±5°范围内变化且幅度随时间减小，变化频率为 5 Hz；转速为 20 r/ s且以 2 r /s的速度减至16 r /s。 红外传感器噪声为均值为零，均方根为10-4g的随机白噪声。图7所示即为在上述仿真条件下，弹载三轴红外传感器的输出曲线。

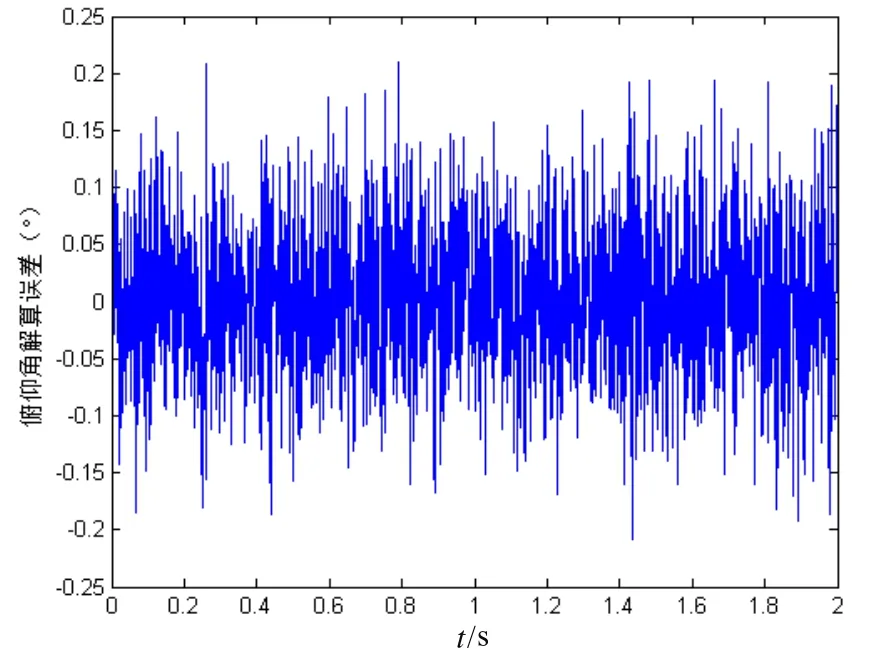
图8 俯仰角解算误差Fig.8 Calculating error of pitch angle

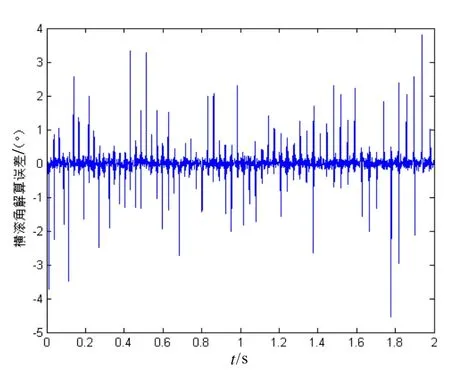
图9 常规解算方案的横滚角解算误差Fig.9 Calculating error of roll angle

图10 改进解算方案的横滚角解算误差Fig.10 Calculating error of roll angle after improving

首先采用常规的解算方案对弹丸的姿态角进行解算。图8所示为俯仰角的解算误差，误差在±0.3°以内；图9所示为横滚角的解算误差，误差在±5°以内。由数值仿真结果可知，采用常规解算方案的横滚角解算误差比较大，因此采用改进的解算方案，交替使用Ty或Tz来解算横滚角。图10所示即为改进解算方案的横滚角解算误差，误差在±0.5°以内。与常规解算方案相比，横滚角解算误差范围降低近10倍，进一步提高了姿态角的解算精度和测量信号的有效利用率。

4 结 论

基于地球红外辐射场测量弹丸滚转姿态是一种低成本、小体积，易于工程实现的测量方法。本文结合相关理论和实际工程需要，通过对地球红外辐射场的产生机理与特性进行了深入分析，建立了弹载红外传感器测量模型，改进了常规的姿态解算算法。结果表明，改进的姿态解算算法将横滚角误差范围降低近10倍。相比传统姿态测量传感器，红外传感器具有体积小、重量轻、无漂移、成本低等优点，并且具备全天候、昼夜使用的测量能力。该测量方法可以用于旋转飞行体的姿态测试，具有十分宽广的应用前景，为姿态测试的新型化和多元化打下基础。

（References）：

[1] 向超, 卜雄洙, 李玎. 基于三正交磁传感器的新型旋转弹体定姿方法[J]. 中国惯性技术学报, 2011, 19(4): 443-446. Xiang C, Bu X Z, Li D. New spinning projectile's attitude measurement based on three pairwise-orthogonal magnetic sensors[J]. Journal of Chinese Inertial Technology, 2011, 19(4): 443-446.

[2] Herrmann P, Bil C, Watkins S, et al. Simulation and flight test of a temperature sensing stabilization system[J]. Aeronautical Journal, 2005, 109(1094): 167-176.

[3] 续立军, 刘涛, 陈海昕, 等. 一种用于无人机姿态测量的红外地平仪算法改进[J]. 中国惯性技术学报, 2014, 22(4): 474-480. Xu L J, Liu T, Chen H X. Improved algorithm for UAV attitude estimation using infrared horizon detector[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 474-480.

[4] 吴成富, 冯拮, 马松辉. 一种基于红外温度传感器的无人机姿态测量方法[J]. 电子设计工程, 2012, 20(17): 141-145. Wu C, Feng Z, Ma S. An attitude measurement for UAV based on infrared sensor[J]. Electronic Design Engineering, 2012, 20(17): 141-145.

[5] Egan G K, Taylor B. Characterisation of infrared sensors for absolute unmanned aerial vehicle attitude determination[R]. Monash Univ. TR MECSE-2007, Melbourne, Australia, 2007: 142-149.

[6] Nguyen T. Attitude determination using infrared earth horizon sensors[C]//AIAA/USU Conference on Small Satellites. 2014: 1-8.

[7] Egan G K, Taylor B. The use of infrared sensors for absolute attitude determination of unmanned aerial vehicles [R]. Tech. Rep. MECSE-22-2006, Monash University, Australia, 2006: 125-132.

[8] Rogers J, Costello M. A low-cost orientation estimator for smart projectiles using magnetometers and thermopiles[J]. Navigation, 2012, 59(1): 9-24.

[9] 李晓雨, 马春林, 支炜, 等. 基于红外传感原理的无人机姿态测量系统设计[J]. 传感器与微系统, 2014, 33(9): 101-103. Li X Y, Ma C L, Zhi W. Design of attitude measurement system for UAV based on infrared sensing principle[J]. Transducer and Microsystem Technologies, 2014, 33(9): 101-103.

[10] Tokutake H, Kuribara M, Yuasa Y, et al. Attitude sensing system using photo-detectors[C]//International Workshop on Instruction for Planetary Missions. 2012: 1022-1024.

Attitude measurement of spinning projectile based on earth infrared radiation field

YU Jing, BU Xiong-zhu, YANG Bo, WANG Xin-zheng
(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Since the precision of the current micro-inertial sensors could not meet the requirements of spinning projectile’s attitude precision, a low-cost attitude detection system is designed by using the thermopile sensors according to the characteristic of earth infrared radiation field. First, the generation mechanism of the earth infrared radiation field is studied, and the variation of infrared radiation rate between sky and earth is analyzed. Then, the measurement model of thermopile sensors is established by combining with the motion feature of spinning projectile during flight. In order to obtain the attitude information, the functional relation between the attitude and the sensor output is derived. Finally, the attitude algorithm is modified based on the error propagation principle, which further improve the utilization of sensor output. The result indicates the high precision of this algorithm. The calculating error of pitch angle and roll angle are within ±0.3° and ±0.5° respectively by this improved algorithm. The detection system is simple and practical, and meets the requirements of spinning projectile’s attitude measurement.

spinning projectile; earth infrared radiation field; error analysis; attitude algorithm

U666.1

A

1005-6734(2015)04-0511-05

10.13695/j.cnki.12-1222/o3.2015.04.017

2015-04-09；

2015-07-28

国家机电动态控制重点实验室基金（9140C360203120C36134）；江苏省普通高校研究生科研创新计划项目（KYZZ_0115）

于靖（1989—），男，博士研究生，从事组合导航研究。E-mail：njustyujing@126.com

联 系 人：卜雄洙（1966—），男，教授，博士生导师。E-mail：buxu105@mail.njust.edu.cn