空间稳定平台通用误差模型

高钟毓，贺晓霞，何虔恩

（清华大学 精密仪器系，北京 100084）

空间稳定平台通用误差模型

高钟毓，贺晓霞，何虔恩

（清华大学 精密仪器系，北京 100084）

自由转子陀螺是一种二自由度机电陀螺，其漂移特性可应用二次型漂移误差模型描述。从二次型漂移误差模型出发，推导了壳体翻滚条件下的调制平均漂移误差模型，并推广到空间稳定平台上工作的极轴陀螺和赤道陀螺；列写了二次型陀螺漂移误差模型驱动下的空间稳定平台标称运动方程；经过扰动线性化，求解出平台标称运动轨迹增量坐标的解析表达式；基于扰动线性化模型并考虑到加速度计测量误差，证明了观测变量为纬度误差、经度误差及冗余轴转角误差时，空间稳定平台运动方程的17项误差系数都是可辨识的；分析了该17项误差系数的估计精度与加速度计组合件测量误差的关系。仿真和实验结果表明本文提出的通用误差模型是有效的。

空间稳定平台；自由转子陀螺；漂移误差；模型辨识

惯性导航系统误差模型是系统误差分析与控制的基础。目前，研究惯性导航系统误差模型的文献很多，其中研究统一误差模型或通用误差模型的有文献[1-8]等。文献[9]针对不同机械编排的惯性导航系统，给出了相应的详细的系统误差方程，并指出误差模型具有等价性。但是，对于不同形式的惯性导航系统，惯性仪表被稳定在不同的测量参考坐标系中，加速度计和陀螺仪本身具有的测量误差将通过不同的坐标变换折合到相同的导航解算坐标系，所形成的误差驱动函数是不一样的。因此，它们作用于相同的误差模型，将会引起不同的时间响应——误差传播特性。

惯性导航系统是一种非线性、时变系统，由各种各样的误差源激励出不同的误差传播特性。最主要的误差源有陀螺仪漂移误差、加速度计测量误差(偏置、标度因子及非线性等)、陀螺平台框架伺服系统误差，以及地球重力模型误差等。通常，采用陀螺壳体旋转或台体旋转等技术措施来调制平均陀螺仪与壳体相关的常值漂移角速度，以达到自动补偿效果，这是非常必要和有效的。文献[10]中已经给出了静电陀螺14个误差系数的二次型漂移误差模型经过壳体旋转调制后，只剩余4个误差系数，本文对于更为通用的20个误差系数的模型经壳体旋转调制后的形式进行了推导，并给出了此误差模型驱动下的空间稳定平台标称运动方程；同时考虑了加速度计通用误差模型，推导了空间稳定平台运动方程的17项误差系数通用模型，并证明这些系数都是可辨识的。

1 二次型陀螺漂移误差模型

对于任何二自由度机电陀螺，引起陀螺漂移的自变量只有作用于陀螺的比力矢量f =(fxkfykfzk)。采用一般表示式，陀螺漂移角速度(ωdx,ωdy)可表示为

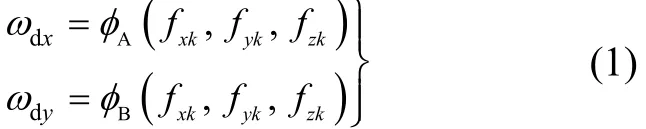
式中，φj(·)(其中j=A,B)表示比力矢量的函数。式(1)展开成泰勒级数，可得

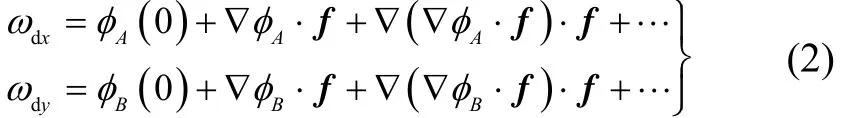
该二次型陀螺漂移误差模型普遍适用于任何型式的二自由度机电陀螺。然而，不同型式的陀螺具有不同的误差源，模型系数对总漂移的贡献也是不同的。例如，静电陀螺基于保守的静电干扰力矩而导出的漂移模型仅含14个系数［10］。与二次型漂移误差模型相比较，其减少了6项漂移系数，即 D(A)yfy、D(A)xyfxfy、D(A)yzfyfz、D(B)xfx、D(B)xyfxfy、D(B)xzfxfz等。这6项漂移系数反映了作用于陀螺的非守恒力矩（如剩余磁场的电磁干扰力矩、剩余气体的阻尼力矩）、正交不平衡力矩及结构交叉变形耦合滤波效应等。

2 陀螺壳体翻滚条件下的漂移误差模型

当陀螺壳体翻滚时，壳体坐标系中的比力可表示为

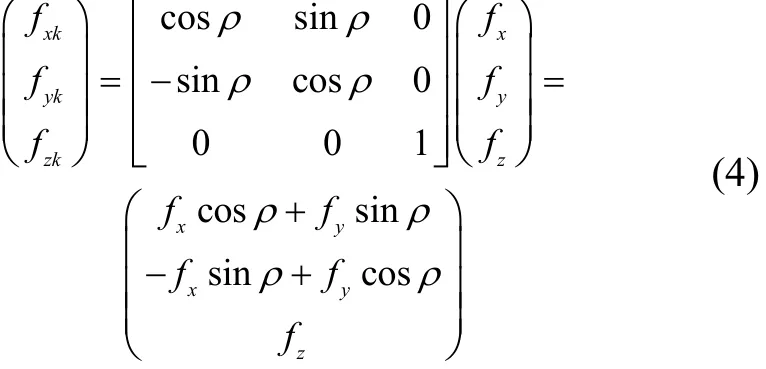
式中：fx,fy,fz是平台坐标系中表示的陀螺受到的比力；ρ=ρ˙t+φ0为壳体翻滚角。将式(4)代入式(3)可得

在壳体翻滚条件下，调制后的陀螺漂移角速度可表示为

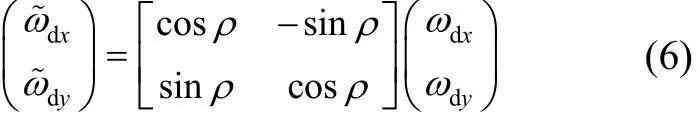
将式(5)代入式(6)，可得壳体翻滚调制后的陀螺漂移角速度。

考虑到空间稳定平台相对地球的旋转角速度非常缓慢，其变化频率近似于地球自转角速率ωie，而陀螺壳体翻滚的角频率比舒拉频率ωs还高10～20倍。因此，在求取调制后的陀螺漂移角速度(ω˜dx,ω˜dy)对壳体翻滚周期T=2π/ρ˙的平均值时，可将稳定平台上的加速度计组合件输出的比力矢量(fx,fy,fz)近似为常量。于是，利用正余弦函数的正交性，可得调制平均后的陀螺漂移角速度和为

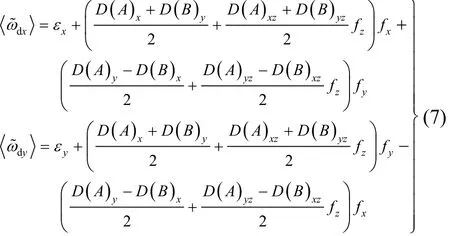
式中，xε、yε表示沿X轴和沿Y轴调制平均后剩余的g0项漂移误差。注意，采用四位置壳体翻滚与陀螺壳体连续旋转一样，式(7)都是成立的[9]。

3 空间稳定平台上的陀螺漂移误差模型

参考图1，平台由里到外，由稳定元件（台体）、内框、中框及外框组成。在稳定元件上安装三轴加速度计组合件和两只自由转子陀螺。其中，一只陀螺的动量矩矢量平行地轴，另一只的动量矩矢量平行赤道平面，分别称为极轴陀螺和赤道陀螺。赤道陀螺通过冗余环安装在台体上，冗余环的转轴平行于平台坐标系的YP轴，在初始时刻与中环轴一致。

图1 空间稳定平台原理图Fig.1 Mechanism of space stable platform

极轴陀螺输出的二自由度角度信号分别控制内环轴和中环轴上的伺服电动机。赤道陀螺输出的二自由度角度信号分别控制台体轴和冗余轴的伺服电动机。外环轴伺服电动机，根据平台工作状态，由内环轴或台体轴上的角度传感器信号控制。

空间稳定平台上的陀螺仪保持不施加指令力矩，工作在自由陀螺状态，消除了陀螺仪力矩器的附加误差，可充分发挥陀螺仪潜在的精度。

由于平台是空间稳定的，因此，平台上的加速度计组合件测量的是运载体在空间稳定坐标系中的比力矢量(fxP,fyP,fzP)。在空间稳定平台上，极轴陀螺坐标系与平台坐标系名义上一致，动量矩矢量平行于台体轴。即H1//ZP。因此，极轴陀螺坐标系中的比力矢量(f1x,f1y,f1z)等于(fxP,fyP,fzP)。于是，在壳体翻滚条件下，极轴陀螺调制平均后漂移误差模型可由式(7)表示为

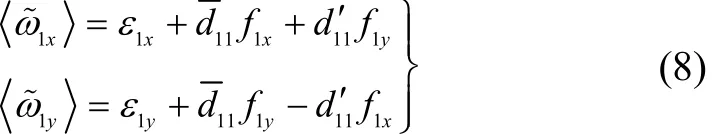
空间稳定平台上的赤道陀螺动量矩矢量与平台的XP轴一致。作用于赤道陀螺的比力矢量为(f2x,f2y,f2z)，可计算如下：

这里，Yr表示平台冗余轴转角。

由于赤道陀螺的壳体转轴沿着X轴，其输出轴分别为Y轴和Z轴，因此在壳体翻滚条件下，利用式(7)，通过坐标变换x→y、y→z及z→x，赤道陀螺的漂移误差模型可表示为

引入符号：

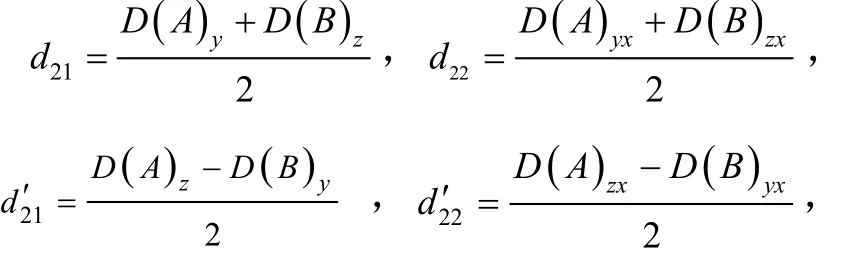
则赤道陀螺漂移误差模型可简化为

4 空间稳定平台运动方程及其解

［9］中的公式（5.109），空间稳定平台的标称运动方程可表示为

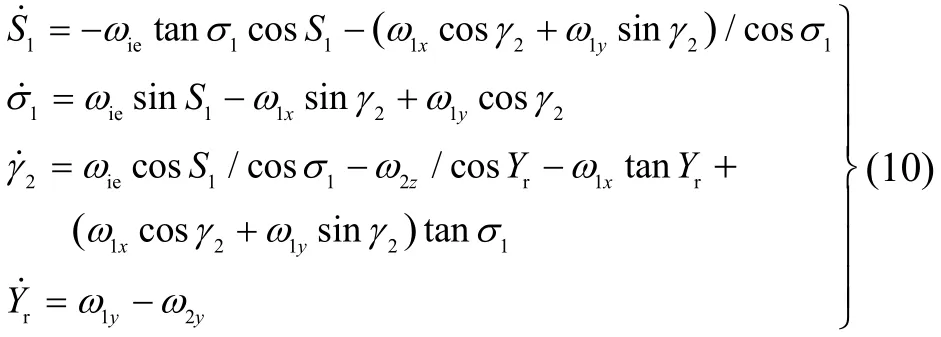
式中，(ω1x,ω1y)和(ω2y,ω2z)分别为极轴陀螺和赤道陀螺的漂移角速度。二次型陀螺漂移误差模型在壳体翻滚条件下，分别如式(8)和式(9)所示。

令XPYPZP（P系）、XeYeZe示（e系）及NED（n系）分别表示空间稳定平台坐标系、原点在地心的地球坐标系及本地水平指北坐标系（又称地理坐标系）。假设XPYPZP相对XeYeZe的三个欧拉角为（-S1,σ1,-γ2），那么，由e系到P系的方向余弦矩阵为

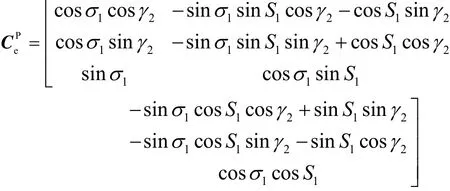
由n系到e系的方向余弦矩阵为

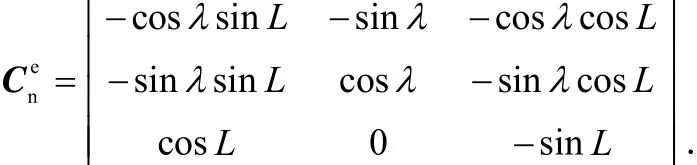
式中，S1、σ1为角分级的小角度。因此，由n系到P系的方向余弦矩阵可近似为

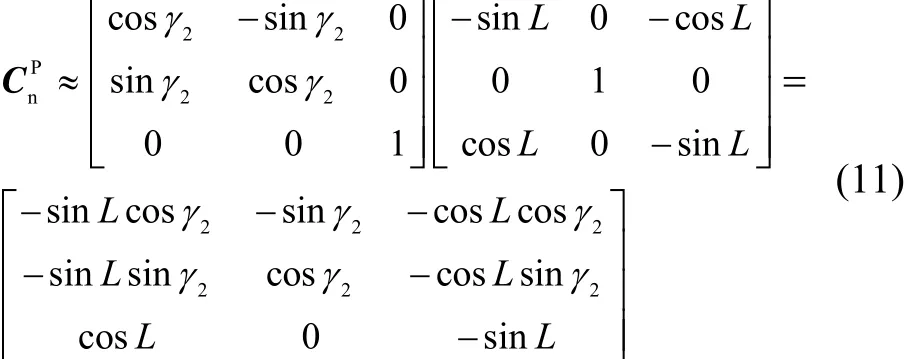
于是，在静止基座上，或者低速巡航运载体上，重力加速度g在P系（即，极轴陀螺坐标系）中引起的比力矢量为

式中，第二等式已经令g=1。

将作用于极轴陀螺的比力代入极轴陀螺漂移误差模型(8)，可得

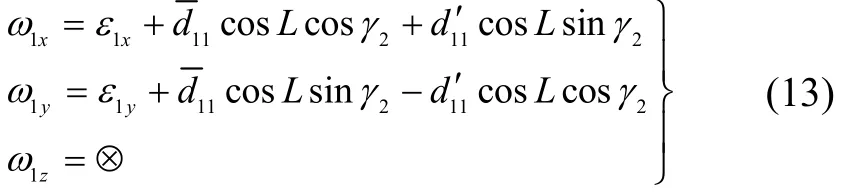
式中，d11=d11+d12sinL 。而作用于赤道陀螺的比力矢量可表示为

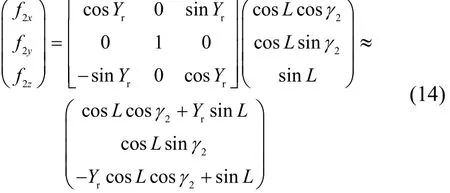
将式(14)代入赤道陀螺漂移误差模型(9)，在略去二阶小量的条件下，可将赤道陀螺漂移误差模型简化为

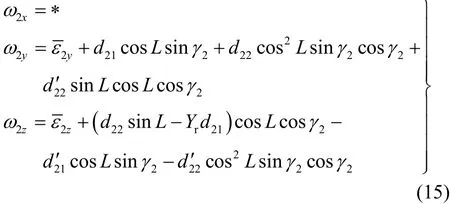
将极轴陀螺漂移误差模型(13)和赤道陀螺漂移误差模型(15)代入式(10)，可得四环空间稳定平台运动方程为

空间稳定平台运动方程组(16)经过扰动线性化处理，可得线性化误差模型为

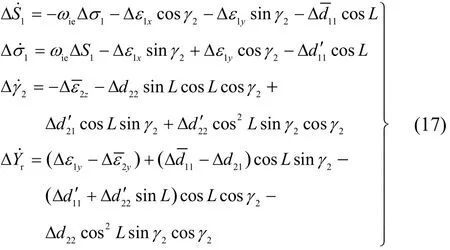
下面，让我们联立求解方程组(17)中的第一式和第二式。不失一般性，令，且˙2-ωie）为小量。求解结果，可得

5 通用误差模型及其可辨识性

除了陀螺，影响导航误差的还有加速度计误差Δfe，考虑加速度计误差后，令

式中，z1、z2为观测变量如下：

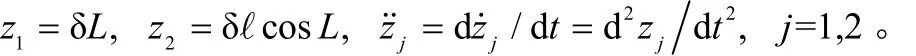
根据纬度误差δL、经度误差δℓcosL，可得[9，P386]：

利用上述各个表达式，可将方程(19)及冗余轴转角误差ΔYr改写为

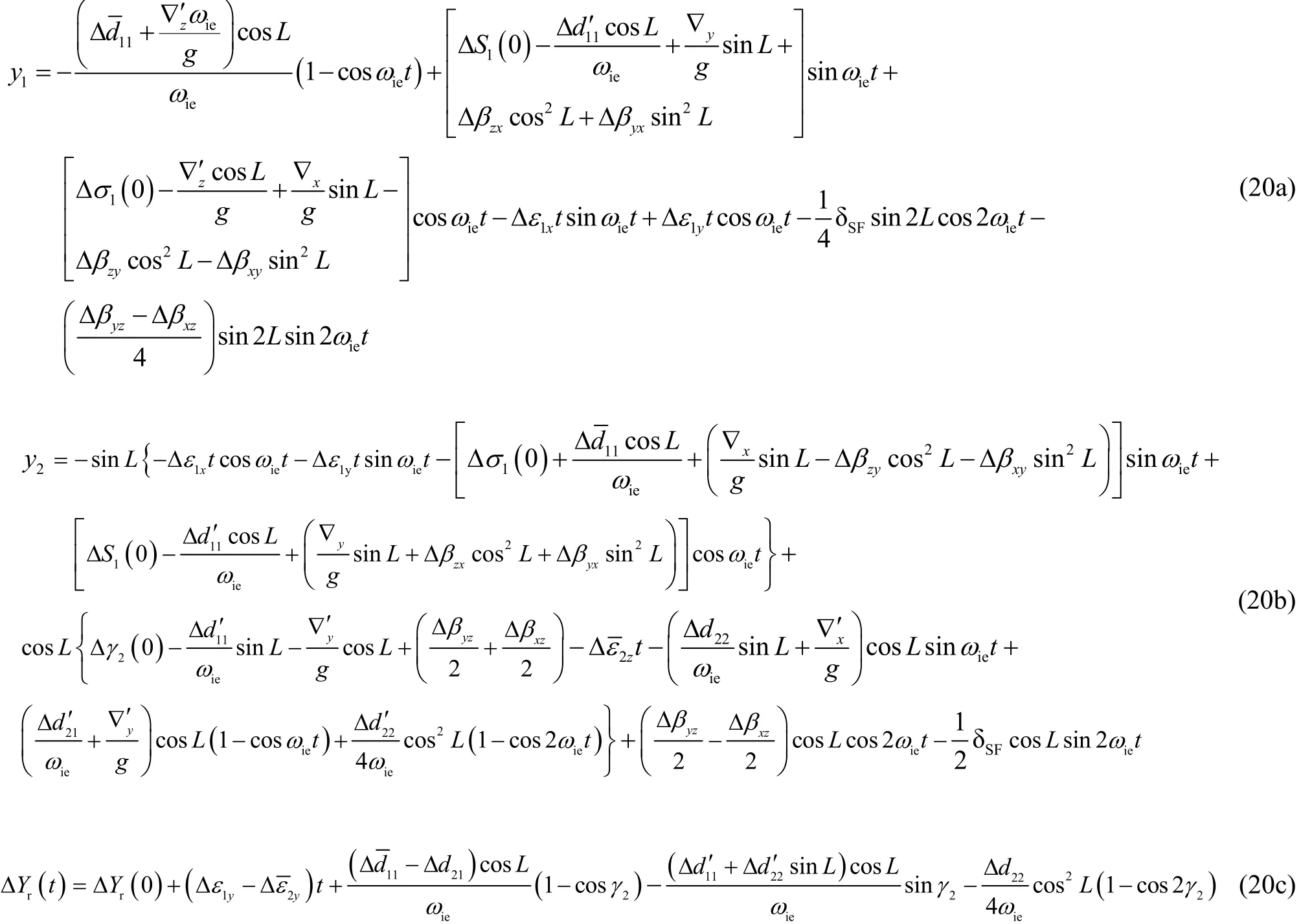
由新的观测方程(20a)～(20c)，易见，利用等式右边各项系数的正交性，根据观测变量序列，我们可得下列估计值：

① 由｛y1（ti）｝可以独立估计及

② 在已知上述估计的基础上，由｛y2（ti）｝可以估计

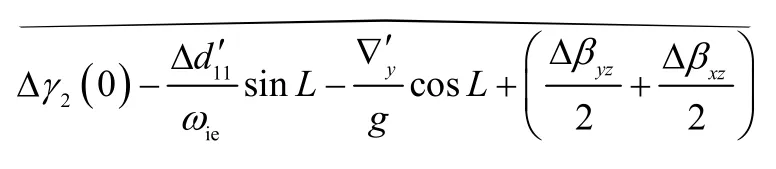
③ 在已知上述估计的基础上，由｛ΔYr（ti）｝可以估计

④ 最后，还可以进一步分离下列参数：

至此已经证明空间稳定平台的所有17项误差系数都是可以辨识的，其中包括：

① 平台4项失准角：

② 极轴陀螺4项漂移误差系数：

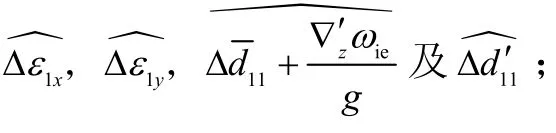
③ 赤道陀螺6项漂移误差系数：

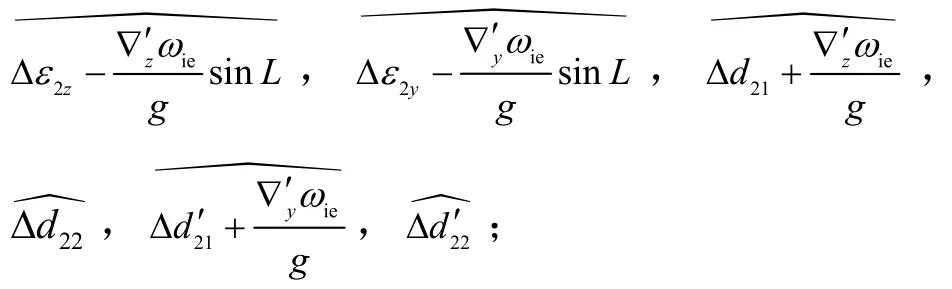
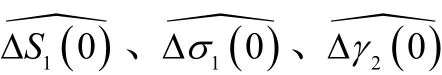
6 仿真及实验结果

先根据以下步骤产生仿真数据：

Step 1. 设置平台三个角和冗余轴的初始转角；

Step 2. 根据式(12)(14)求出作用于极轴、赤道陀螺的比力矢量；

Step 3. 设置陀螺漂移误差系数和壳体翻滚失调角、角速度，根据式(3)(4)和步骤2得到的比力矢量，求极轴、赤道静电陀螺漂移角速度；

Step 4. 把步骤3求得的漂移角速度代入式(16)，用数值微分方程求解微分方程，产生平台三个失调角及冗余轴转角；

Step 5. 设置加速度计误差系数，根据式(19)求观测变量；

Step 6. 把产生的仿真数据代入卡尔曼滤波器，用48 h数据得到待估计参数，然后利用估计出的参数预报后10天的平台角或经纬度误差并与理论值做差，得到预报残差。

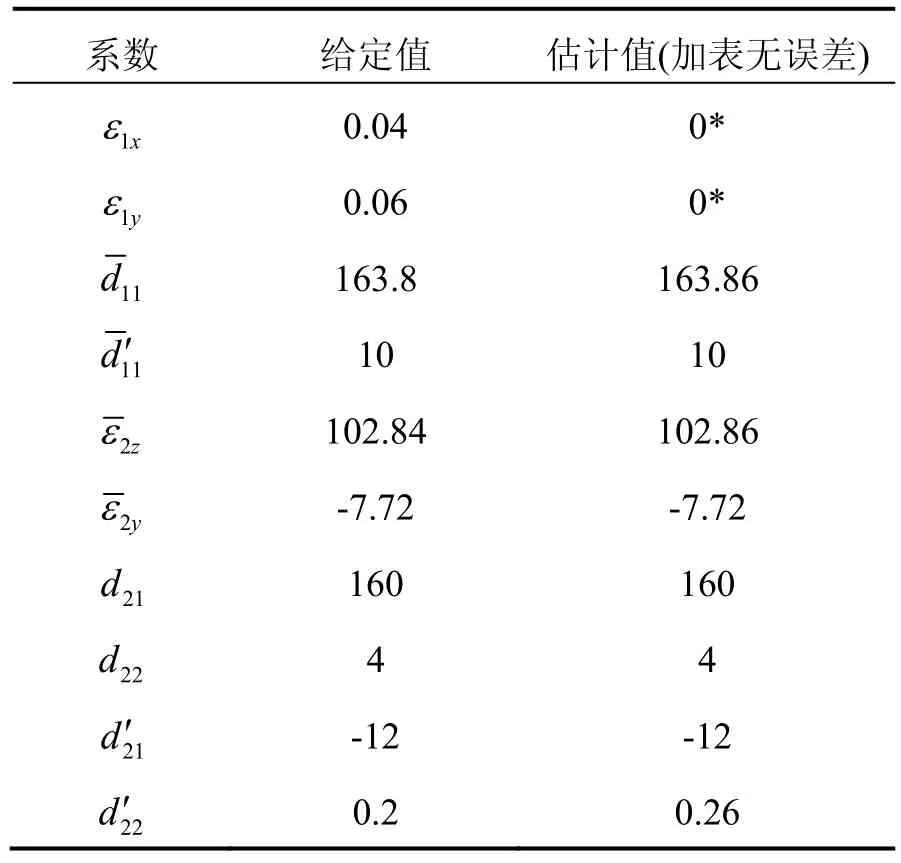
表1 不考虑加表误差时，用平台角和冗余轴转角估计结果Tab.1 Estimation result by using platform angle and redundancy angle without considering accelerometer error

图2 不考虑加速度计误差时平台角和冗余轴角的预报残差Fig.2 Predicted residuals of platform angle and redundancy angle without considering accelerometer error

以下是仿真试验结果：

① 不考虑加表误差，根据式(16)建立14状态卡尔曼滤波器，估计值如表1所示，平台角预报残差如图2所示（其中，各系数均作了归一化处理，下同）。

由图2和表1可见，10项陀螺漂移误差系数估计精度优于1%，各平台角预报误差优于0.0005/10 days，说明14个漂移系数的估计都是无偏的。

② 考虑加表误差，根据式(20)，估计17个系数。加速度计误差给定值如表2所示，估计值如表3所示，经纬度预报残差如图3所示。

由图3和表3可见，10项陀螺漂移误差系数、3项加速度计误差系数估计精度优于1%，经纬度预报误差优于0.012/10 days，比实际使用需要小250倍，说明17个系数的估计都是精确的。

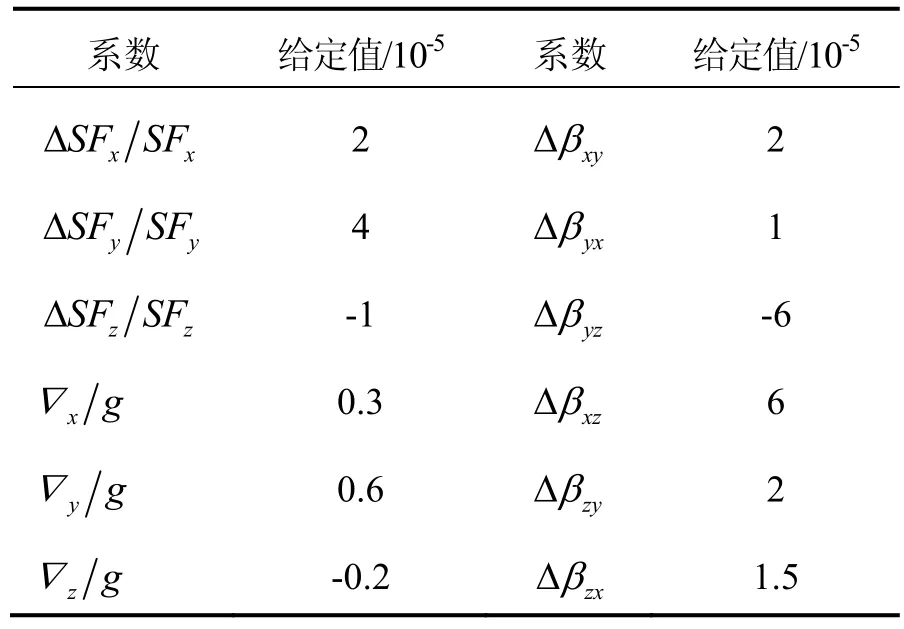
表2 加表误差给定值Tab.2 Accelerometer errors

表3 考虑加表误差时，用经纬度和冗余轴转角估计结果Tab.3 Estimation results by using longitude, latitude and redundancy angle with considering accelerometer error

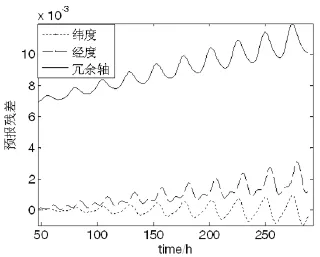
图3 考虑加速度计误差时经纬度和冗余轴转角的预报残差Fig.3 Predicted residuals of longitude, latitude and redundancy angle with con sidering accelerometer error

③ 实验结果

图4是某次实验的系数收敛情况及导航误差曲线，图中，对导航误差进行了归一化，最大值“1”设置为给定指标的1/3，实验情况表明新的通用误差模型能满足实际使用需要。

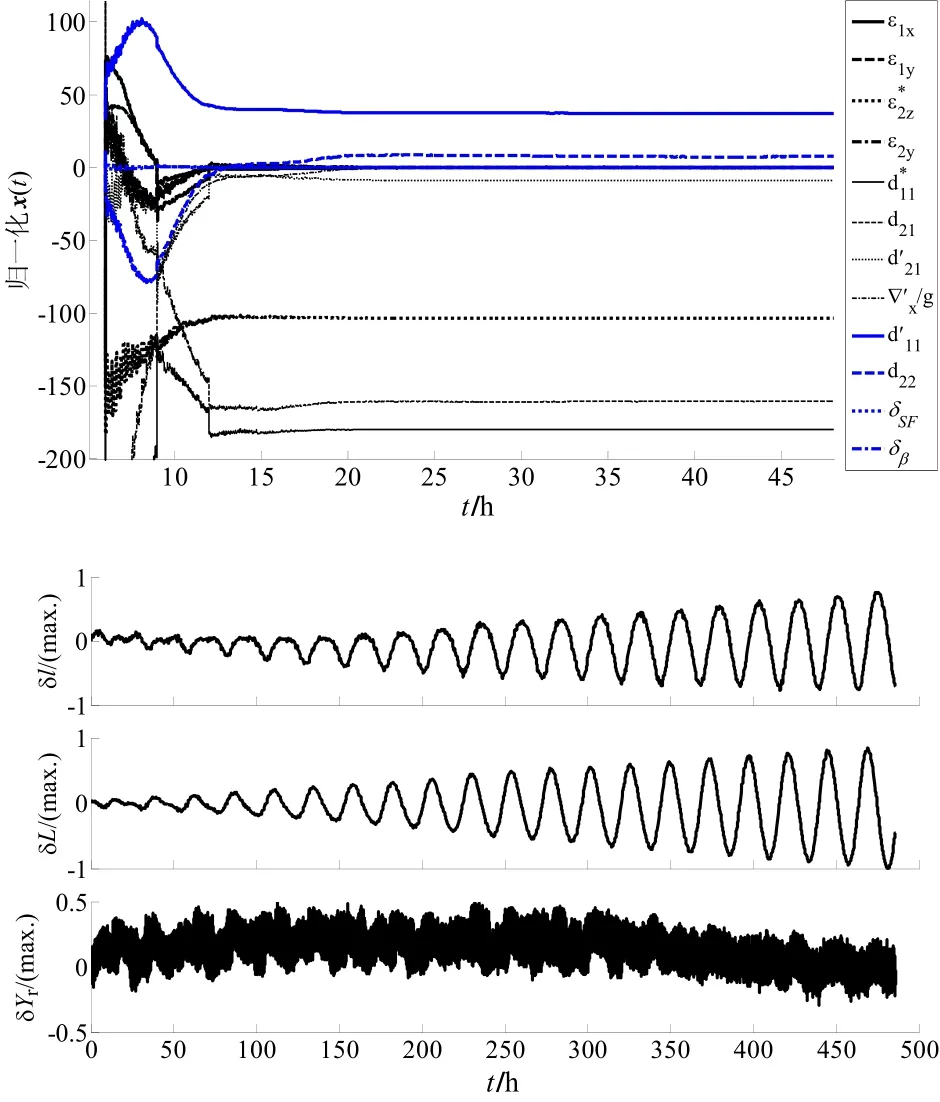
图4 某次实验的系数收敛情况及导航误差曲线Fig.4 State estimation and navigation error

7 结 论

① 通用二次型陀螺漂移误差模型含有20个漂移系数，但在壳体翻滚条件下可简化为6系数模型。进一步，对于空间稳定平台上的极轴陀螺和赤道陀螺，可分别简化为4系数模型和6系数模型。

② 对于二自由度机电陀螺空间稳定平台，在陀螺壳体翻滚条件下，平台所具有的17项误差系数（含4项平台失准角、10项陀螺漂移系数及3项加速度计组合件测量误差系数），都是可辨识的。

③ 在有加速度计组合件测量误差条件下，3项平台失准角和3项陀螺g1项漂移误差系数的估计是有偏的。为了消除该6项估计的有偏性，必须验前精确标校加速度计组合件的测量误差模型。这样，平台的17项误差系数可减少3项，且剩余的14项误差系数估计都是无偏的。

参考文献（References）：

[1] Groves P D. Principles of GNSS, inertial, and multisensor integrated navigation systems[M]. Artech House Publishers, 2nd Revised Edition, 2013.

[2] Blankinship K G. A general theory for inertial navigation eror modeling[C]//2008 IEEE/ION PLANS. Monterey, CA, 2008: 1152-1166.

[3] Bekir E. Introduction to modern navigation systems[M]. World Scientific publishing Co Pte Ltd, 2007.

[4] Goshen-Meskin D, Bar-Itzhack I Y. A unified approach to inertial navigation system error modeling[J]. Journal of Guidance Control and Dynamics, 1992, 15: 648-653.

[5] Arshal G. Error equation of inertial navigation[J]. Journal of Guiadance, Control, and Dynamics, 1987, 10(4): 351-358.

[6] Bar-Itzhack I Y, Goshen-Meskin D. Identity between INS position and velocity error models in the true frame[J]. Journal of Guidance, 1988, 11(6): 590-653

[7] 张和杰, 常国宾. 旋转调制式捷联惯导误差分析[J]. 海军工程大学学报, 2011, 23(5): 55-59 Zhang He-jie, Chang Guo-bin. Error analysis of rotation modulating strapdown inertial navigation system[J]. Journal of Naval University of Engineering, 2011, 23(5): 55-59

[8] Zhang Lun-dong, Lian Jun-xiang, Wu Mei-ping. Error model of rotary ring laser gyro inertial navigation system[J]. Journal of Beijing Institute of Technology, 2010, 19(4): 439-444.

[9] 高钟毓. 惯性导航系统技术[M]. 北京: 清华大学出版社, 2012.

[10] 高钟毓. 静电陀螺仪技术[M]. 北京: 清华大学出版社, 2005.

[11] 何虔恩, 高钟毓, 吴秋平. 空间稳定系统壳体翻滚失准角误差精确补偿[J]. 中国惯性技术学报, 2014, 22(5): 572-575. He Qian-en, Gao Zhong-yu, Wu Qiu-ping. Accurate compensation for case rolling misalignment angle in space-stable systems[J]. Journal of Chinese Inertial Technology, 2014, 22(5): 572-575.

General error model for space stable platform

GAO Zhong-yu, HE Xiao-xia, HE Qian-en
(Department of Precision instrument, Tsinghua University, Beijing 100084, China)

The drift model of a 2-D free-rotor mechanical gyroscope is usually in quadratic form of specific force. Based on this form, the mean drift model modulated by case rotation-dwell device is derived for both the polar and equatorial gyroscopes on space stable platform. Following this mean drift model, the normal movement of the space stable platform can be modeled and analytically expressed by using perturbation theory. Based on the perturbation linearization model and taking into account the accelerometer’s measurement error, it is proved that the 17-coefficients of the space stable platform are all observable when the observed variables are errors of latitude, longitude and redundancy frame angle. The relationship between the estimation precision of the 17 coefficients and the accelerometer’s measurement error is analyzed and numerically simulated. The simulation and experiment results demonstrate the efficiency of the general error model.

space stable platform; free rotor gyroscope; drift model; model identification

U666.1

A

1005-6734(2015)04-0421-08

10.13695/j.cnki.12-1222/o3.2015.04.001

2015-02-18；

2015-07-09

国防科技预研项目（51309050202）

高钟毓（1936—），男，教授，从事惯性导航研究。E-mail：gaozy@tsinghua.edu.cn

联 系 人：贺晓霞（1977—），女，副研究员，从事惯性元件、系统研究。E-mail：hexx@tsinghua.edu.cn