基于智能集成架构的时间序列数据挖掘算法研究*

张人上，安俊娥

（1.山西财经大学信息管理学院，太原 030006；2.中国电子科技集团第三十三研究所，太原 030006）

基于智能集成架构的时间序列数据挖掘算法研究*

张人上1，安俊娥2

（1.山西财经大学信息管理学院，太原 030006；2.中国电子科技集团第三十三研究所，太原 030006）

针对单一算法在处理复杂时间序列数据时存在缺陷以致无法挖掘全部信息的问题，提出了智能集成架构，给出了4种集成结构，并分析了它们的适用情况。针对一类随机噪声干扰的时间序列数据，采用并联嵌套建模结构，提出嵌套双种群粒子群算法的自回归滑动平均（ARMA）模型，用于挖掘数据中的随机性趋势；提出基于概率密度控制（PDF）的最小二乘支持向量机（LSSVM），用于挖掘数据中的确定性趋势，两种模型并联补集成实现对数据信息的充分挖掘。通过一组实验验证了所提方法的效果。

时间序列，支持向量机，智能集成，自回归滑动平均

0 引言

随着信息时代的到来，大数据分析已成为各个领域愈来愈重视与依赖的技术手段。通过时间序列数据挖掘，能够掌握事物的发展规律，从而对其未来趋势进行预测。

本文提出了智能集成架构，针对一类随机噪声干扰的时间序列数据，采用并联嵌套建模结构，提出嵌套双种群粒子群算法的自回归滑动平均模型，用于挖掘数据中的随机性趋势；提出基于概率密度控制的最小二乘支持向量机，用于挖掘数据中的确定性趋势，两种模型并联补集成实现对数据信息的充分挖掘。通过一组实验验证了所提方法的效果。

1 智能集成架构

智能集成模式挖掘方法的形式与结构主要包括4种：

第1种称为并联补集成，其结构包括两个子模型，两个模型没有主次之分，且相互之间互为补充。该结构中的两个子模型通常由两种建模方法得到，单一建模方法能够挖掘时间序列数据中的部分信息以获知对应规律，但由于方法所限，无法获知数据中的全部信息，因此，依靠两种建模方法互为补充以充分挖掘数据中隐含的规律或模式。

叠加形式分为相加与相乘两种。并联叠加集成结构如图1、图2所示。图中X1为模型1的输入，Y1为模型1的输出，Y1=f1（X1）。X2为模型2的输入，δ为模型2的输出，δ=f2（X2）。在图1中Y=Y0+δ，在图2中Y=δY0。

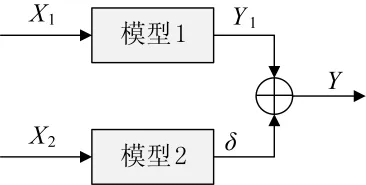
图1 相加形式的并联补结构

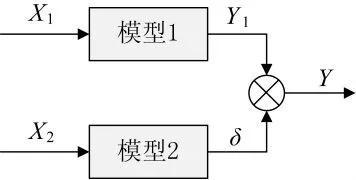
图2 相乘形式的并联补结构

第2种称为加权叠加集成，该结构由多个子模型加权后叠加构成，其中每个子模型对应的权重大小决定了它在集成模型中所起的作用。该结构中的多个子模型通常由多种建模方法得到，单一建模方法能够挖掘时间序列数据中的部分信息以获知对应规律，但由于方法所限，无法获知数据中的全部信息，因此，依靠多种建模方法互为补充以充分挖掘数据中隐含的规律或模式。

图3 加权并集成结构

第3种为串联集成，该结构包括两个或多个子模型，其中一个子模型的输出为另一个子模型的输入。非线性动态系统通常采用这种形式，比如采用神经网络反映系统静态时的非线性特性，采用NARMX（具有外生变量的非线性自回归滑动平均）表征动态特性。串联集成结构如图4所示。

第4种为模型嵌套集成，该结构包括至少两个子模型，其中一个称为基模型，用来对工业过程的主体结构进行建模，其他子模型则嵌套在基模型中，用来对基模型中的未知参数建模，如图5所示。比如将蚁群算法、粒子群优化算法、遗传算法等仿生算法应用到系统辨识中，用来实现模型中的参数估计。

图4 串联集成结构

图5 模型嵌套集成

2 嵌套双种群粒子群算法的ARMA模型

ARMA时间序列模型理论非常完善，对于一个平稳、零均值的时间序列，如采取合适的阶次与系数，能保证拟合出的模型预报残差为零均值噪声。

本文提出双种群粒子群优化算法（cPSO），其中一个子群执行自适应网格粒子搜索，以保持种群的多样性，提高算法的全局搜索能力；另外一个子群按照快速收缩粒子群算法搜索，具有非常出色的收敛性能。采用cPSO算法优化确定ARMA模型的阶次与系数以最小化模型预报残差。

算法步骤如下：

第1步：采用单位根检验法（ADF）对时间序列数据进行平稳性检验，如果序列为零均值平稳序列则直接用于ARMA模型建模，否则需要对时间序列数据进行平稳化处理；

第2步：设置模型阶次与系数优化准则为模型预报的均方根误差最小化；

第3步：采用cPSO算法拟合ARMA模型系数与阶次。

cPSO算法原理如图6所示，算法步骤如下：

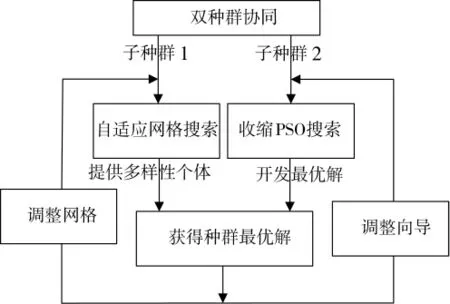
图6 cPSO算法流程

A、划分网格

将每一维决策变量平均分成gp段。

B、划分子种群

将整个种群分为两个子群即自适应网格搜索子群（简称网格子群）与收缩PSO子群（简称PSO子群），两个子种群的粒子个数分别为Popz与Pops。

C、种群初始化

在每一个格子内都随机生成一个粒子pxq∈R2，从而构成网格子群，{pxq|q=1，…，Popz}。另外，在整个决策空间内随机生成Pops个粒子，从而得到PSO子群{pxq|q=Popz+1，…，Popz+Pops}。令PSO子群的初始速度为0，第k个粒子的初始个体向导pbestq为自身即pbestq=pxq，q=Popz+1，…，Popz+Pops，初始全局向导gbest为随机选择的某个粒子位置。

D、向导调整

根据优化准则即模型预报误差均方根最小化评估每个粒子，得到 feval（pxq），q=Popz+1，…，Popz+Pops，并按照下式调整PSO子群的个体向导与全局向导：

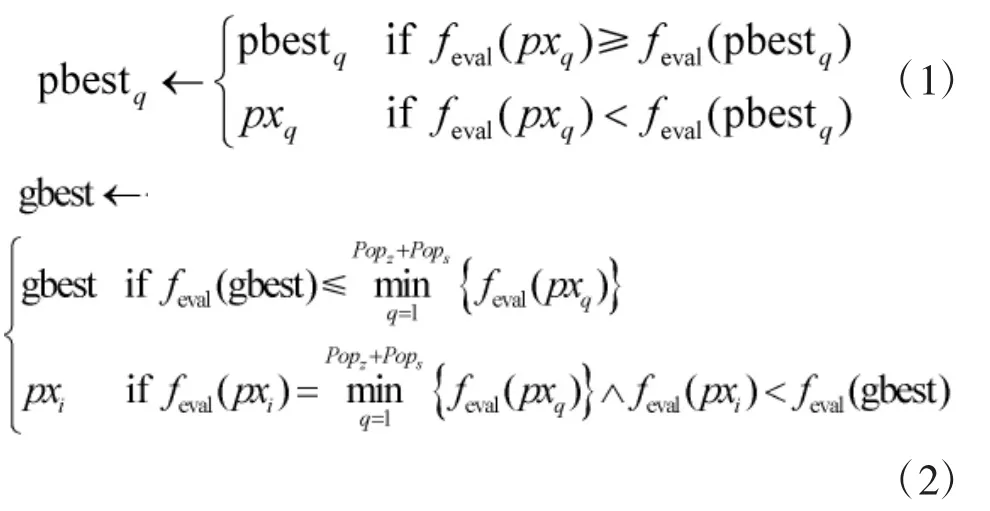
E、网格调整

根据gbest所在格子（这里称为向导网格）的位置调整每个网格粒子的搜索范围。调整后使所有网格粒子的搜索范围都包括向导网格区间。如图7所示，为了表述简单，假设将每一维决策变量范围分成3段，两维空间，因此，总共分割成9个网格，其中gbest位于第5个网格内。在调整前粒子1的搜索范围为网格1，调整后粒子1的搜索范围变为网格1、2、4、5构成的空间。同样，在调整前粒子2的搜索范围为网格2，调整后粒子2的搜索范围变为网格2、网格5构成的空间。

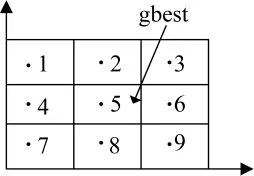
图7 网格调整实例

F、网格子群位置更新

网格子群的位置pxq（q=1，…，Popz）按照下式进行更新：

G、PSO子群位置更新

收缩 PSO子群的位置 pxq（q=Popz+1，…，Popz+Pops）按照下式进行更新：

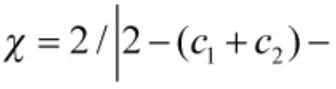
第4步：验证所建立的时间序列ARMA模型。

3 基于PDF的LSSVM

提出了一种新的LSSVM模型参数选择准则即使模型残差PDF逼近给定的高斯分布，以提高数据分析与预测的精度与泛化性。PDF调整与控制思想起源于随机控制领域，其目标是使系统输出的概率密度函数跟踪一个给定的分布形状。

算法原理如下：

LSSVM将优化问题描述如下：

其中，ζj∈R是残差，C是惩罚系数。

建立Lagrangian函数，并根据Karush-Kuhn-Tuc ker（KKT）条件，得到：

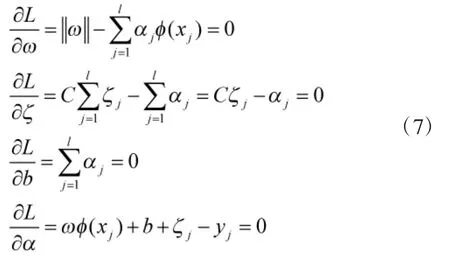
消除ω，ζ后，得到线性方程：

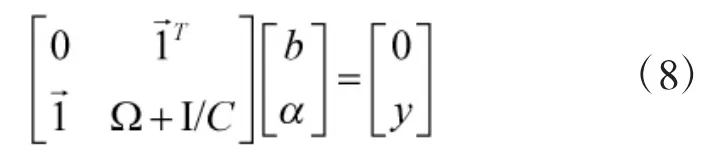
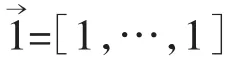
核函数取高斯径向基函数

则，待求LSSVM回归模型为：

其中，αj，b由方程组式（8）求解得到。

在LSSVM回归建模过程中，惩罚系数C和核函数参数σ是可调参数，一旦选择出这两个参数，则可以获得最小二乘支持向量机模型。

基于残差PDF控制的LSSVM数据分析与预测原理是利用系统输入输出的数据，在模型结构确定的基础上，调整模型内部参数使模型误差方差最小且具有零均值。因此，在系统的输入、输出存在随机干扰时，该方法仍然能够保证建模精度。如果随机干扰为高斯分布，因此，调整模型参数的目标是使得模型残差概率密度函数（PDF）越窄越好。如果随机干扰为非高斯分布，以模型可调参数为输入，模型残差的概率密度函数为输出分布，通过建立关于输入的在线调整算法，实现输出概率密度函数跟踪一个定义在一个窄区间上的零均值高斯分布。下面详细介绍这一参数选择准则，并采用标准网格搜索算法［20］确定LSSVM模型参数的过程。

残差ξ可以表示为：

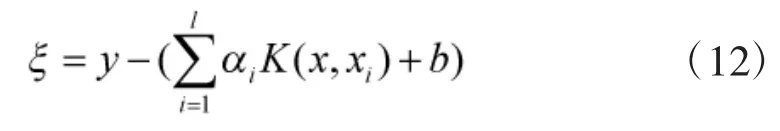
进一步可以写成如下函数形成：

设残差ξ的概率密度分布为γξ，则γξ为可调参数惩罚系数C和核函数参数σ的函数，即γξ（x，y，C，σ），因此，可以通过调整C和来使γξ接近于一目标高斯分布。

设目标高斯分布概率密度函数γtarget为：

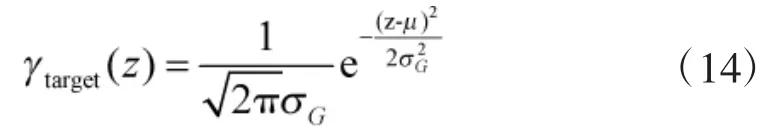
定义参数选择准则：

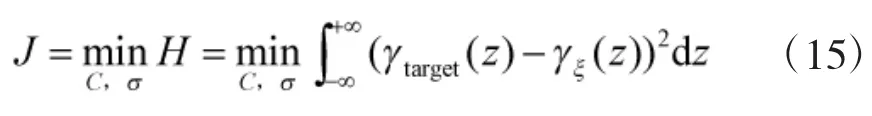
4 实验研究

针对一类随机噪声干扰的时间序列数据，本文采用上述并联嵌套建模结构，采用子模型嵌套cPSO的ARMA模型挖掘数据中的随机性趋势；采用基于PDF的LSSVM挖掘数据中的确定性趋势，两种模型并联补集成实现对数据信息的充分挖掘。

以选矿生产过程时间序列数据为收集对象，该数据集受到严重的工业噪声干扰。

分别采用本文所提方法（ARMA-LSSVM）与单纯的PDF-LSSVM分别对上述工业对象进行数据分析与预测，给定的目标高斯概率密度函数的均值μ=0，方差σ2G=7.5。模型验证结果显示在图8～下页图13中。

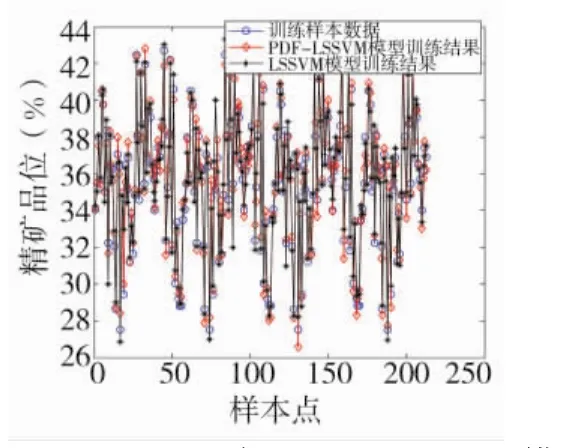
图8PDF-LSSVM与ARMA-LSSVM模型训练结果与样本数据对比

图9PDF-LSSVM与ARMA-LSSVM模型预报结果与测试数据对比

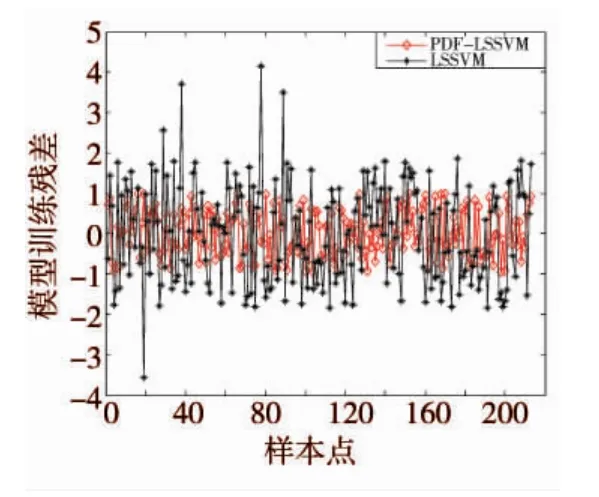
图10PDF-LSSVM与ARMA-LSSVM模型训练残差

图8显示了PDF-LSSVM与ARMA-LSSVM模型训练结果于训练样本数据的拟合程度，图10反映了PDF-LSSVM与ARMA-LSSVM模型训练精度。由图8可以发现，两个方法的模型训练结果都能近似拟合上训练样本数据，图10结果显示两个方法的模型训练精度都能满足要求，并且ARMA-LSSVM具有一定的优势。

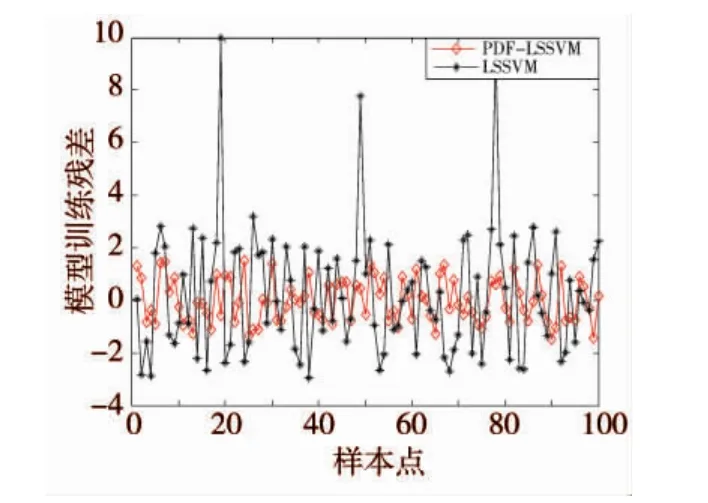
图11PDF-LSSVM与ARMA-LSSVM模型预报残差

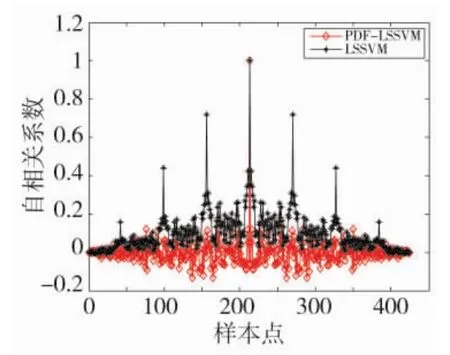
图12PDF-LSSVM与ARMA-LSSVM训练模型残差的自相关分析

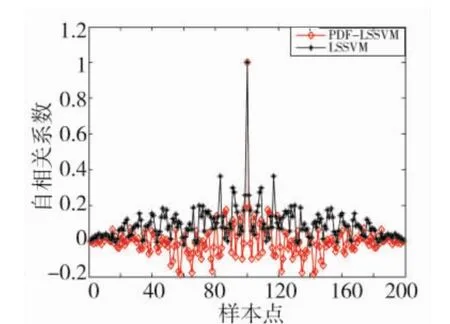
图13PDF-LSSVM与ARMA-LSSVM预报残差的自相关分析

图9为PDF-LSSVM与ARMA-LSSVM模型预报结果与测试数据的对比，图11为PDF-LSSVM与ARMA-LSSVM模型预报精度。根据图9、图11，ARMA-LSSVM建模方法的预报精度要高于PDF-LSSVM建模方法，这说明ARMA-LSSVM的泛化性要高于PDF-LSSVM建模方法，因此，其建模结果更具有实际应用价值。

图12、图13为PDF-LSSVM及ARMA-LSSVM模型训练残差、预报残差的自相关分析。根据该图，可以发现PDF-LSSVM模型的训练残差与预报残差均不为白噪声，即PDFLSSVM所建模型没有提取出建模对象的全部信息，造成模型精度不高、泛化性差等问题。与之相比，ARMA-LSSVM模型的训练残差与预报残差近似为白噪声，因此，其模型结果具有更高精度与应用价值。

［1］孙翔，王景成.基于回归模型的城市长期水量预测［J］.微型电脑应用，2010，38（11）:7-9.

［2］才让加.化学数据的一元线性回归分析［J］.青海师范大学学报（自然科学版），2005，29（2）:13-15.

［3］姚伟.税收组合预测仿真研究［J］.计算机仿真，2012，39（10）:374-377.

［4］叶宗裕.非线性回归模型参数估计方法研究-以C-D生产函数为例［J］.统计与信息论坛，2010（1）:41-45.

［5］张金旺，刘红，华琳，等.非线性回归模型拟合生存资料分析［J］.数理医药学杂志，2009，29（6）:641-642.

［6］Ratkowsky D A.Nonlinear Regression Modeling-a Unified Practical Approach［M］.Marcel Dekker Inc，1983.

［7］张新波.时间序列模型在税收预测中的应用［J］.湖南税务高等专科学校学报，2010，25（4）:30-32.

［8］林锦朗.时间序列模型在海关税收预测中的应用［J］.统计与咨询，2009，28（1）:26-27.

［9］王时绘，周健.时间序列数学模型在税收分析中的应用［J］.科技广场，2011，31（7）:150-154.

［10］张伏生，汪鸿，韩悌，等.基于偏最小二乘回归分析的短期负荷预测［J］.电网技术，2003，25（3）:27-31.

［11］肖苏，熊炎.基于灰度统计和神经网络的物流税收预测模型［J］.物流技术，2013，35（23）:131-132.

Research on Time Series Data Mining Algorithm Based on Intelligent Integrated Architecture

ZHANG Ren-shang1，AN Jun-e2
（1.Shanxi University of Finance and Economics，Taiyuan 030006，China；
2.The Thirty-third Research Institute of China Electronic Technology Group Corporation，Taiyuan 030006，China）

Aiming for the setbacks that a single algorithm can't dig all information in dealing with complex time-series data defects，the intelligent integrated architecture is proposed，providing four kinds of integration architecture，and analyzing their application.Time-series data for one category of random noise，utilizing series nested modeling structure，proposes Auto Regressive Moving Average model（ARMA）nested with double population particle swarm optimization algorithm for date mining，and figures out its stochastic trends;a probability density control based on support vector machine is provided，aimed to determine the trend of data mining，two categories of model of parallel compensation are set to implement the objective of thoroughly data mining，via a series of experiments that revealed the effectiveness of the proposed method.

time series，Support Vector Machine（SVM），intelligent integrated，ARMA

TP393

A

1002-0640（2015）03-0067-05

2014-01-18

2014-03-27

山西省自然科学基金资助项目（20120005）

张人上（1978－ ），男，山西忻州人，硕士，讲师。研究方向：计算机应用、网络安全。