SVC和SOFM组合聚类的雷达信号预分选方法

戴胜波，雷武虎，程艺喆，曾 礼，王 迪

（1.脉冲功率激光技术国家重点实验室，合肥 230037；

2.安徽省电子制约技术重点实验室，合肥 230037；3.解放军63623部队，甘肃 酒泉 732750）

SVC和SOFM组合聚类的雷达信号预分选方法

戴胜波1，2，雷武虎1，2，程艺喆1，2，曾 礼3，王 迪1，2

（1.脉冲功率激光技术国家重点实验室，合肥 230037；

2.安徽省电子制约技术重点实验室，合肥 230037；3.解放军63623部队，甘肃 酒泉 732750）

由于采用单一聚类方法对雷达信号聚类分选中，存在一定的问题。为了克服单一聚类的缺点，并利用其优点，提出了采用组合聚类的方法对雷达信号进行聚类分选。在分析了自组织特征映射网络（SOFM）与SVC的原理的基础上，利用SOFM和SVC的优点，设计了一种SOFM与SVC组合聚类的方法，实现对雷达到达角（DOA）数据的聚类分选。理论分析与实验仿真表明，该方法能够克服噪声的影响，与有先验信息条件下的K均值聚类结果相比，取得了较好的聚类分选结果。

自组织特征映射网络，支持向量聚类，组合

0 引言

分选密集的雷达信号需要对脉冲进行分流和稀释。聚类是对雷达信号进行预分选的一种有效方法［1］。对含方位角和仰角的二维信息的到达角（DOA）参数，是雷达信号参数中最稳定的参数，是预分选处理的重要参数。对DOA进行聚类分选可以有效达到预分选的目的。

支持向量聚类（SVC）是一种无监督的聚类方法，在雷达信号分选上具有广泛的研究［2-6］。相对于其他传统的聚类方法，SVC不需要其他先验知识，根据雷达DOA数据分布情况完成聚类，避免了信号分选中容差设置的局限性，特别适合对复杂未知雷达辐射源信号类别的聚类和识别。然而，SVC的缺点，一方面在于对较大样本的数据运算时间长，另一方面受自身参数C，q的影响，导致聚类数目变化。为了解决这两个问题，文献［2-6］探讨了将数据分段耦合处理的方法、快速支持向量等方法和自适应调整参数C，q的方法。参数C，q的自适应调整，需要对SVC方法执行多次，同样增加了处理时间。因此，克服这两个问题的关键在于SVC处理的数据是小样本。SVC算法的优点在于处理小样本数据。

由于SOFM网络强大的自我学习能力，SOFM能将输入空间的样本模式类有序地映射在输出层上，将高维空间的样本在保持拓扑结构不变的条件下投影到低维空间，具有强大的数据特征提取能力［7］。因此，借助SOFM，大样本数据的处理可以转化为对小样本数据的处理。为此，基于SOFM网络和SVC的优点，提出一种组合聚类方法，对雷达信号进行分选。即对DOA数据进行SOFM学习训练，提取出DOA数据的拓扑结构，然后对该拓扑结构进行SVC聚类，得到聚类数目和聚类中心，完成DOA聚类分选。

1 组合聚类算法

组合聚类是组合不同聚类算法进行聚类的方法，该方法旨在充分利用不同聚类算法的优点，达到最佳的聚类结果。

1.1 SVC算法

SVC的基本思想是：任意输入数据空间{xj，j=1，…，N}，采用一个非线性变换Φ把xj映射到高维特征空间。在该空间中，寻找一个最小半径的封闭超球体，可将数据映射为球面上的点和非球面上的点。超球体空间的球体之外，称作约束支持向量（Bounded Support Vector，BSV）；位于超球体空间的球体的表面，这样的点称作支持向量（Support Vector，SV）。根据数据在超球体空间的分布关系，建立数据之间的邻接矩阵。然后对邻接矩阵进行深度搜索，自动找出数据的聚类情况。

SVC方法由于经过了核函数的映射，有可能较好的分辨、提取并放大有用的特征，使原来没有显现的特征突现出来，从而能够更好地聚类［2］。

1.2 SOFM神经网络

SOFM的结构通常由两层神经结构构成，由输入层和输出竞争层构成，如图1所示。输入层中的每个神经元分别与输入特征矢量的每一维分量相对应，即输入层神经元的数目n与输入特征矢量的维数一致；输出层（即竞争层）是由M=p×q个神经元构成二维的网络结构，每个神经元节点均与其周围的神经元侧向连接。其学习方法是［7］：

（1）初始化。对网络的输出层各权向量赋一个小的随机数，得到wij（0），j=1，2，…，M，i=1，2，…，n，初始化各个神经元的邻域Njc（0）。

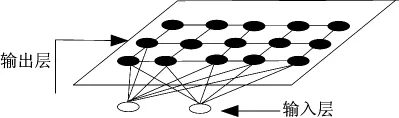
图1 二维SOFM结构

（2）接受输入。从样本中随机输入一个样本模式作为网络的输入样本Xi，i=1，2，…，n。

（3）寻找获胜神经元节点。计算输入样本Xi与所有输出层神经元之间的欧拉距离，从中选出距离最小值所对应的神经元，即为获胜的神经元节点，满足式（1）

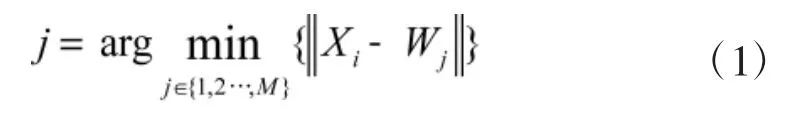
（4）调整权值。获胜神经元j的邻域Njc（t）内的所有神经元进行调整：

η（t）为学习速率因子，是随着时间t的递减函数，且η（t）∈（0，1），保证算法的收敛性。

（5）返回步骤（2），直到学习速率η（t）小于某个预定的值或兴奋神经元与输入样本稳定对应为止。

SOFM是一种无导师的学习人工神经网络，能够对不同的输入样本模式进行学习，将不同的输入模式有序地映射在输出层上，其权值反映了输入数据模式的分布特征，即可利用SOFM对数据进行特征提取。

1.3 组合聚类算法实现

SVC的方法能够自动聚类在于其复杂的二次规划求解，处理小样本数据具有较好的适用性。SOFM方法能提取出数据的拓扑结构，具有较好用少量样本代替全部样本的特性。考虑到这两个优点，可以将SOFM与SVC组合起来进行聚类。即先利用SOFM提取出数据的拓扑结构，然后对拓扑结构进行SVC处理。这种组合聚类方法目的是减少直接对大数据进行SVC的处理时间。

由于每部雷达的DOA信息不能迅速变化，DOA参数具有较好的稳定性，经常作为雷达信号聚类分选的首选参数。含有方位角和仰角的二维信息的雷达DOA参数，其二维平面的分布（拓扑结构）表现为一个个方形或者圆形的簇分布。这样的特征结构很适合SOFM的提取，因此，利用SOFM和SVC的组合聚类方法很适用于DOA数据。

但是，如果噪声数据不滤除的话，将对后续的SVC聚类产生较大的影响。实际中DOA数据中含有噪声，SOFM提取DOA数据特征时，不仅提取了信号数据的特征，同时也提取了噪声数据的特征。在SOFM网络中表现为：部分神经元的权值由信号数据产生（本文称为信号神经元），部分神经元的权值由噪声数据产生（本文称为噪声神经元）。对SOFM的权值进行SVC聚类，由于SVC处理的数据量较少，噪声神经元的权值将对SVC产生较大的影响。为了减少噪声神经元对SVC的影响，需滤除SOFM网络中的噪声神经元，保留SOFM中的信号神经元，才能真实反映信号DOA数据的结构。另一方面，由于SOFM网络自身的原因，需要滤除对输入数据无响应的死神经元。对于含有噪声的DOA数据，滤除噪声和噪声神经元的具体方法如下［9-10］：

（1）将DOA数据按照式（1）的原则分配到SOFM相应的神经元上，检查每个神经元拥有的数据个数。滤除少于2个数据的神经元，排除了相应的死神经元和部分噪声神经元。

（2）对剩下的每个神经元j，计算分配到神经元j的数据的平均值centerj，计算权值Wj与centerj的距离distj=‖Wj-centerj‖，并计算所有距离distj的平均值mean_distj和标准方差std_distj，如果对某个神经元满足式（3），则将该神经元视为噪声神经元，排除该噪声神经元，也滤除分配到该神经元的数据。

（3）对剩下的每个神经元j，计算属于神经元j的每个数据xi与权值Wj的距离distj（xi）=‖xi-Wj‖，并且计算所有distj（xi）的均值mean_distj和标准方差std_distj。如果神经元j中的数据xi满足式（4），则删除该数据xi。可以滤除部分输入噪声数据。

（4）对于整个SOFM，属于每个神经元数据的平均个数为N/M。对于剩下的神经元，统计属于每个神经元数据的个数，如果其个数小于N/M，则将其神经元列入待排除的神经元。对于待排除的神经元j，统计其属于各个待排除的神经元的数据num_j，计算 num_j的平均值 maen_num_j和方差std_num_j。如果方差大于平均值，即std_num_j＞maen_num_j，且神经元j满足式（5），则将该神经元排除掉，并删掉属于其的数据；如果方差小于平均值，即std_num_j＞maen_num_j，且神经元j满足式（6），则将该神经元排除掉，并删掉属于其的数据。

综上所述，组合聚类算法具体的流程如图2所示。

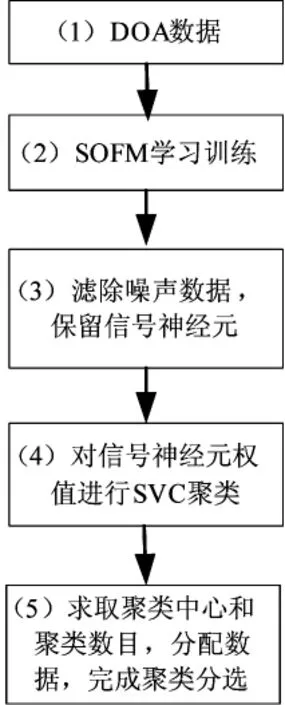
图2 SOFM和SVC的组合聚类算法流程

2 仿真结果及分析

2.1 算法原理仿真

雷达脉冲到达角DOA的参数如表1所示。仿真的DOA数据（3 428个）中含有部分均匀随机噪声数据（100个），其平面散点图如下页图3所示。对该数据进行组合聚类算法，其过程和结果如图3～图7所示。SOFM采用的网络大小为6×6，对DOA数据进行了500次训练。图3为SOFM提取的DOA拓扑结构。图4所示的是滤除噪声神经元后，SVC对信号神经元进行聚类时产生的支持向量。图5所示的是对保留的神经元进行聚类的结果，其聚类个数统计直方图如图6所示。图7所示的是利用图5求出聚类中心后，将DOA数据分配到各个类中的分配结果。从图3～图7可以说明该方法的可行性。为了比较该方法的有效性，在给定原始DOA聚类中心和聚类数目的情况下，利用K均值进行聚类的结果如图8所示。从图7和图8可以得出，该算法原理具有可行性。

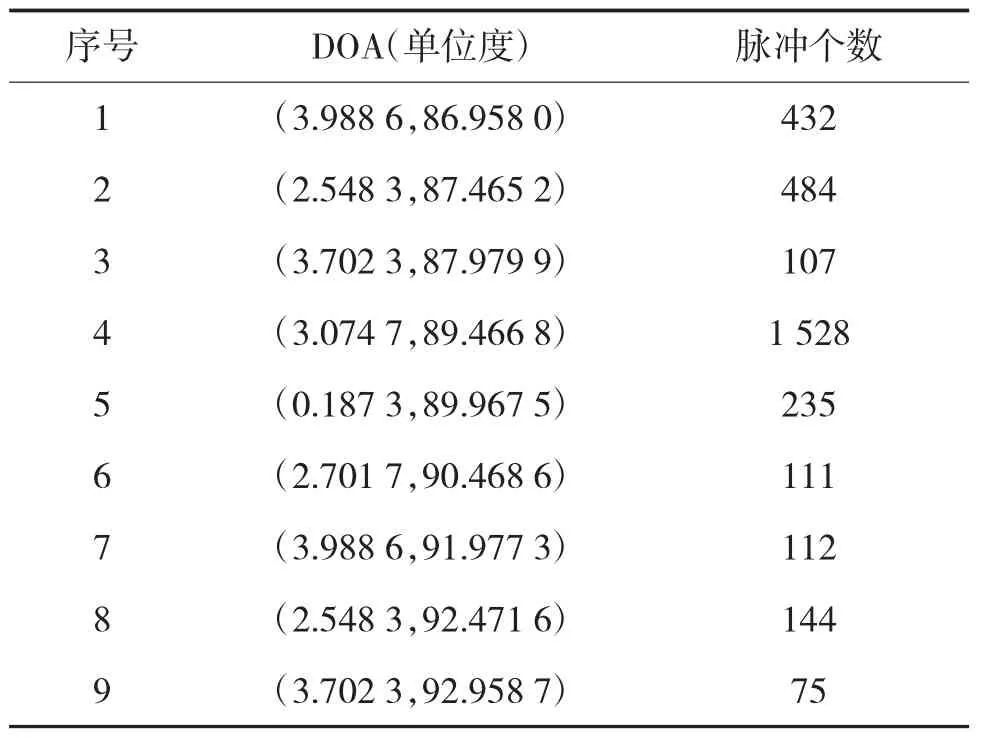
表1 DOA参数表

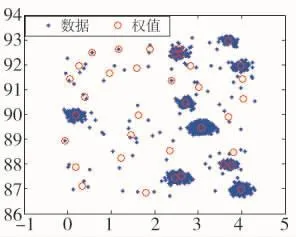
图3 原始数据分布和权值分布

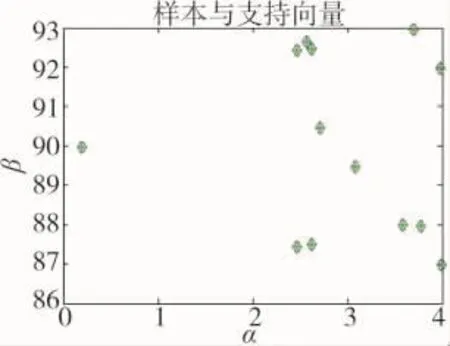
图4 信号神经元的SVC聚类的支持向量

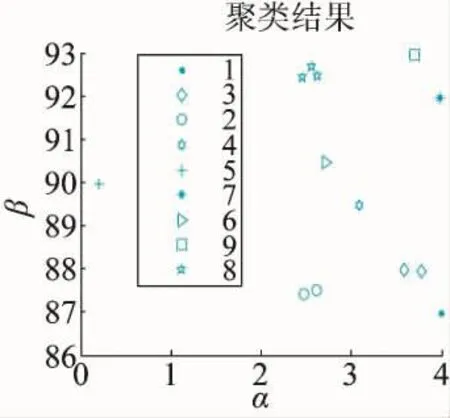
图5 信号神经元的SVC聚类的结果

图6 SVC聚类的直方图

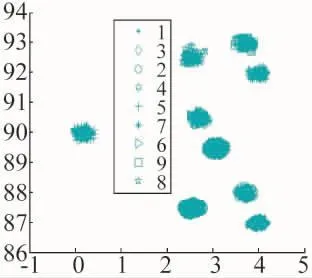
图7 DOA数据组合聚类结果

图8 DOA数据K均值聚类结果

图9 DOA数据组合聚类结果图

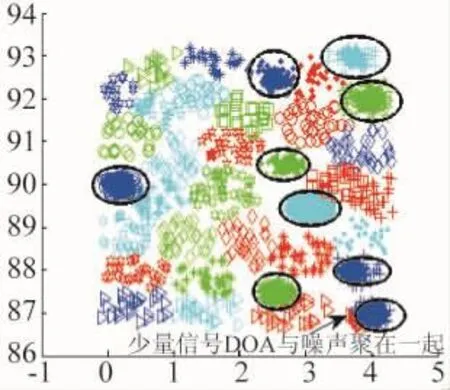
图10 DOA数据组合聚类结果

2.2 算法的抗噪性能分析及运算性能

实际上，噪声数据对该组合聚类的方法存在影响，但是该方法具有一定的抗噪声能力。如图7（含有100个随机均匀噪声），如图9（含有200个随机均匀的噪声），如图10（含有500个随机均匀的噪声）可以看出：对于较少数量的噪声，该算法能够全部去除噪声；对于数量较多的噪声，由于噪声的密度达到一定程度，噪声数据也聚集在一起，因此，噪声不能全部去除。虽然随机均匀分布噪声导致DOA数据的聚类数目增多，但没有破坏DAO的信号数据的特征，信号数据仍然被正确归类。图9、图10中用椭圆圈出了信号DOA数据的聚类结果。图10中，出现了噪声数据与少量信号DOA数据聚在一起的情况。如果噪声的密度继续增大，则噪声将可能破坏信号DOA数据的聚类情况。因此，该算法能适应一定密度的随机均匀分布的噪声影响。同时，该方法可能将具有较少数目的雷达DOA数据当作噪声排除掉，而出现漏分选的情况。

另一方面，该算法处理速度相对直接SVC算法要快。该组合聚类与直接SVC在仿真运算时间上的比较结果如表2所示（在同一计算机上运行的）。直接SVC采用的数据是原DOA数据中选取的部分数据，但所用时间更长，说明组合聚类方法的运算速度具有一定的优势。

表2 算法仿真时间比较

综上，该组合聚类方法能克服噪声的影响，对DOA数据聚类能取得较好的效果，而且减少了运算时间。

3 结束语

SVC聚类方法在雷达信号分选中具有重要作用。为了充分利用SVC的优点，研究了一种对DOA数据聚类的预分选方法，即SOFM与SVC的组合聚类方法，同时分析了噪声对该方法的影响，并提出了滤除噪声的方法。通过仿真实验表明，该方法能够对DOA数据取得很好的聚类效果，能对噪声具有较好的适应性，有利于后续的信号分选。另外，对噪声神经元的滤除方法还值得进一步研究。

［1］郑子扬，陈永游，张君，等.基于SOFM网络聚类雷达信号分选预处理改进算法［J］.航天电子对抗，2013，29（3）：42-45.

［2］王世强，张登福.基于快速支持向量聚类和相似熵的多参雷达信号分选方法［J］.电子与信息学报，2011，33（11）：2735-2740.

［3］李振兴，卢景双，张国毅，等.一种自动选择参数的雷达辐射源SVC分选方法［J］.电子信息对抗技术，2011，26（2）：15-20.

［4］赵贵喜，穆成新，刘永波，等.改进SVC算法在雷达信号分选中的应用［J］，舰船电子对抗，2012，35（3）：6-9.

［5］向娴，汤建龙.基于改进的支持向量聚类的雷达信号分选［J］.航天电子对抗，2011，27（1）：50-53.

［6］Guo Q，Li Z，Zhang X.Support Vector Clustering and Type-entropy Based Joint De-interleaving/recognition Sys-tem of Radar Pulse Sequence［M］.Intelligent Control and Automation.Springer Berlin Heidelberg，2006.

［7］韩力群.人工神经网络理论、设计及应用［M］.北京：化学工业出版社，2007.

［8］Hun A B，David H，Hava T.Siegelmann，Vladimir Vapnik，Support Vector Clustering［J］.Journal of Machine Learning Research，2001，12（2）：125-137.

［9］Wu S T，Tommy W S，Clustering of the Self-organizing Map Using a Clustering Validity Index Based on Inter-cluster and Intra-cluster Density［J］.Pattern Recognition，2004，37（2）：175-188.

［10］Lee S，Daniels K.Gaussian Kernel Width Generator for Support Vector Clustering［C］//International Conference on Bioinformatics and its Applications，2004.

Research on a Combined SOFM and SVC Clustering Method for Pre-deinterleaving of Radar Pulse

DAI Sheng-bo1，2，LEI Wu-hu1，2，CHENG Yi-zhe1，2，ZENG Li3，WANG Di1，2
（1.State Key Laboratory of Pulsed Power Laser Technology，Hefei 230037，China；
2.Anhui Province Key Laboratory of Electronic Restriction，Hefei 230037，China；3.Unit 63623 of PLA，Jiuquan 732750，China）

Since there are some problems in clustering of radar pulses with single clustering method，it is a question to be solved.To overcome the shortcomings and fully make use of the advantages of single clustering method，a method of combining some clustering methods is proposed. After analyzed the principles of Self-Organizing Feature Map（SOFM）and SVC，a clustering method of combining SOFM and SVC is proposed.With fully making use of the advantages of the SVC，the method can solve the problem of clustering the direction of arrival（DOA）which is one of Radar Pulse parameters.The result of simulation shows that the method is free from some noises and effective in sorting the data of DOA，comparing with the method of K-means under prior knowledge.

SOFM，SVC，combined

TN971

A

1002-0640（2015）03-0096-04

2014-01-09

2014-03-16

戴胜波（1988- ），男，湖南岳阳人，硕士研究生。研究方向：信息处理。