一种基于PRI变化规律的雷达辐射源识别方法
2015-06-15关一夫张国毅王晓峰
关一夫,张国毅,王晓峰
(空军航空大学,长春 130022)
一种基于PRI变化规律的雷达辐射源识别方法
关一夫,张国毅,王晓峰
(空军航空大学,长春 130022)
针对相控阵雷达中某些具有复杂PRI调制样式的工作模式难以准确识别的问题,提出一种通过提取PRI序列变化规律来进行辐射源识别的方法。该方法借鉴了脉冲样本图的模型以及生物信息学中基因序列比对的动态规划思想,较好地解决了某些复杂PRI调制样式不好描述,以及相控阵雷达中一个完整工作模式包含脉冲序列长度太短,以致很难通过统计的方法对其进行准确识别的问题。仿真结果表明该算法的有效性,而且在存在脉冲丢失和干扰脉冲的情况下具有稳健性。
PRI规律,雷达辐射源,识别
0 引言
雷达辐射源识别是电子战系统的关键技术之一,其目的是在分选截获雷达信号的基础上,得到信号中雷达的工作参数,然后利用这些参数获取该雷达的体制、用途和型号等信息[1]。目前的雷达辐射源识别算法可分为两类[2]:一种是基于统计参数建模的识别方法,如专家系统的方法[3]、灰度关联的方法[4]、基于人工神经网络的方法[5]、基于粗糙集理论的方法[6]等等;另一种是基于脉冲参数建模的识别方法,如联合分选识别方法[7]、雷达辐射源的序贯识别方法[8]、脉冲样本图的方法[9]等等。随着现代雷达技术的不断发展,各种复杂体制雷达不断涌现,基于统计参数建模的识别方法很难准确描述信号复杂的变化规律,而且相控阵雷达在其一个完整的工作模式周期中可以只辐射很短的一串脉冲序列就实现其功能,这也给统计处理带来很大困难。
本文借鉴脉冲样本图的模型,提出了脉冲PRI样本的模型,并讨论了其在数据库中的存储方法,针对PRI组变信号的规律特点,完善了这类信号脉冲PRI样本在数据库中的存储方式;通过分析侦收数据发现,脉冲序列的PRI变化规律能够提供很可靠的分类信息,越是复杂的变化规律,其所能提供的分类信息量越大,因此,利用基因序列比对中动态规划的思想,提取出脉冲序列PRI的变化规律并以此作为特征设计了识别匹配度模型,而且针对PRI组变信号的情况,设计了综合识别匹配度的模型。
1 脉冲PRI样本
雷达辐射源按照信号形式可以分为脉冲雷达和连续波雷达两类。连续波雷达的数量较少,并且使用有限,本文主要对脉冲雷达进行研究,所述雷达辐射源均为脉冲雷达。PRI是脉间参数,通过计算两相邻脉冲到达时间差得到。
1.1 脉冲PRI样本的定义
设雷达在某工作模式下发射一串具有N个脉冲的脉冲序列S=(t1,t2,…,tN),其中ti,i=1,2,…,N代表脉冲的到达时间,则P=(PRI1,PRI2,…,PRIN-1)就是该串脉冲的PRI序列,其中PRIj=ti+1-ti,i=1,2,…,N,j=1,2,…,N-1。若从P中选取出一个能准确表示P的子序列P',使得P可近似看作由P'进行周期延拓得到(除了P中开头和结尾的几个PRI值),那么P'就是一个脉冲PRI样本,识别数据库中的已知雷达就是以这种形式进行存储的。P'同时给出了工作样式中PRI值及其排列顺序的信息。
1.2 PRI组变信号的脉冲PRI样本
将PRI脉冲样本作为已知雷达的模型存储在数据库中需要考虑识别准确率和数据库容量之间的折中。不难想到,若将P'延拓两到三个周期再作为样本存入数据库,那么对于足够长的待识别脉冲序列,这样的样本能够对脉冲丢失和干扰脉冲有更强的抗性,但同时增加了数据库的容量。
此外,对于PRI组变信号,其每一组内的脉冲个数可能很多而且并不一定是固定的,如相控阵雷达的一种PRI 3组变样式:在第1组内辐射64个脉冲、第2组48个、第3组32个。因此,需要考虑如何对这类信号建立脉冲PRI样本。现将本文的处理思路讨论如下:将一个工作模式用多个脉冲PRI样本来描述。以这个3组变信号为例来说明,以3个PRI值分别作脉冲PRI样本,即得到3个固定PRI的脉冲样本,每个样本中包含的元素个数根据经验设定,这里认为4个~10个较为合理。在数据库中将这3个样本与同一个工作模式进行关联,在识别时将3个样本的识别结果进行融合作为最终的识别结果。这样就可以较好地解决PRI组变信号脉冲PRI样本的建立问题。
2 算法原理
借鉴生物信息学中基因序列配对的经典算法——动态规划比对算法[10]的主要思想,结合脉冲PRI样本及待识别脉冲序列的特点设计打分矩阵和部分得分矩阵,并将回溯路径所经过的各个点的分值相加,作为计算识别匹配度的依据。该算法的原始算法Needleman-Wunsch算法对于长序列需要建立巨大的打分矩阵和部分得分矩阵,并且在回溯的时候很费时,其时间复杂度和空间复杂度均为O(n2)(n为序列长度),这就限制了其在实际中的应用。后来人们提出了改善其时间、空间复杂度的算法,典型的有:Hirschberg算法、Ukkonen算法和 Divide-and-Conquer算法。其中Divide-and-Conquer算法的时间和空间复杂度分别为O(nlog2d+d2)和O(d)(d为两条序列的得分值),在实际中有较好的应用,对长度为1 000以上的基因序列具有较快的处理速度[11]。关于上述改进算法的原理可参考文献[11],此处不再赘述。
2.1 动态规划的基本原理
首先介绍一下动态规划的基本原理,其过程大致可分为两步:建立得分矩阵和回溯
步骤1:建立得分矩阵M
设有两个序列e1和e2,长度分别为n1和n2,则M是一个(n1+1)×(n2+1)的矩阵,其建立方法如下:首先按照空位得分规则[14]初始化M的第一行和第一列,然后从m22开始,按式(1)计算mij:

其中p(S1i,S2j)表示将M第i行对应序列e1中的元素值与M第j列对应e2中的元素值进行匹配,如果两个数值在预先设定的匹配容差σ范围内则匹配结果为1,否则结果为-1。
步骤2:回溯
回溯是从m(n1+1)(n2+1)开始,沿向左、向上或向左上3个方向,移动到m11的过程。当回溯到mij后,从m(i-1)j,mi(j-1)和m(i-1)(j-1)3个选项中选择满足式(1)
的位置继续前进,直到回溯到m11。
2.2 本文算法流程
本文算法主要分3步:建立自得分矩阵并计算分数,建立互得分矩阵并计算分数,计算识别匹配度。
步骤1:建立自得分矩阵Ma并计算分数Scorea
所谓自得分矩阵就是指e1和e2对应数据库中同一个脉冲PRI样本序列,并由此建立的得分矩阵;计算分数就是对回溯路径上各元素的分值求和,作为该得分矩阵的分数。
步骤2:建立互得分矩阵Mc并计算分数Scorec
所谓互得分矩阵是指e1和e2分别对应上一步中的脉冲PRI样本序列和待识别脉冲PRI序列(或其子序列),并由此建立的得分矩阵;计算分数的方法同上一步。
这里需要说明的是,待识别脉冲PRI序列的选取方法对该算法的处理时间和结果的准确度有很大影响:若用整个待识别脉冲PRI序列计算互得分矩阵,势必要花费大量的时间;若只选取与脉冲PRI样本序列等长度的待识别序列,虽然在理想情况下仍能进行识别,但是由于脉冲丢失和干扰脉冲的存在会使得分矩阵的分值很小以致于误判为未识别的序列。本文对这一问题的处理思路是利用待识别序列中存在大量数据冗余的特点通过多次建立得分矩阵以求取平均分,具体地说,就是截取与脉冲PRI样本序列等长度的待识别脉冲PRI序列,建立互得分矩阵Mc1并计算分数Scorec1,然后以上一次截取序列的末端为起点在待识别序列上向后再截取下一段,建立得分矩阵Mc2并计算分数Scorec2,照此处理L次,最后的得分为:

L通常取3次~5次为宜,若待识别序列长度不能满足这一需求,则按照尽可能多取的原则进行处理。
步骤3:计算识别匹配度η
在对从数据库中选取的脉冲PRI样本计算得分数Scorea,并且将其与一待识别脉冲PRI序列计算得分数Scorec之后,按下式计算二者的识别匹配度η:

并将此作为进行识别判决的依据,若该值超过某一门限则认为识别成功否则为未识别。值得一提的是,互得分矩阵的分数可能为负值,从而使识别匹配度η也为负值,后面的仿真将表明,η为负值时一般是对应序列不匹配的情况,这也使得识别判决门限的设定变得较为容易。
2.3 对于PRI组变信号存在增批时的综合识别匹配度模型
对于PRI组变信号,现有的一些分选算法[13]容易将其分选成多批数据,以上文中提到的PRI 3组变为例,分选算法给出的结果将该信号分成了3组固定PRI的信号,造成了增批,若不对这种情况进行合批处理,就会使识别结果中出现多个重复雷达辐射源的结果,从而给情报分析人员造成困惑。
针对这种情况,结合本文第2部分对组变类型脉冲PRI样本在数据库中存储方式的讨论,建立了一个综合识别匹配度模型。因为组变信号是按固定值分别建立样本,故而当组变信号出现时,就会有多批数据与该信号样式多个样本匹配识别成功,也就是说对于数据库中一个信号样式会得到多个过门限的识别匹配度结果,这时,按下式对这些结果进行融合得到总的识别匹配度:
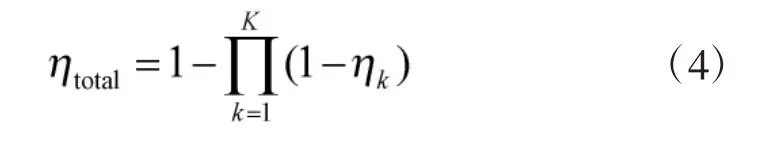
其中ηk表示数据库中该信号样式下第k个样本与某待识别批数据的识别匹配度。
3 仿真结果
下面对该算法的有效性、在存在脉冲丢失和干扰脉冲的情况下算法的稳健性进行仿真说明;文献[12]述及存在一种PRI三编码信号,这种信号具有固定的3个编码值,但是3个值的出现不像参差信号那样具有周期性而是服从某种编码规律,本文对这种信号的识别进行了仿真并分析了仿真结果。由于篇幅所限,仿真只考虑L=1,即只对待识别序列截取一次的情况。
3.1 算法的有效性和稳健性分析
以一个PRI六参差信号为例对算法的有效性和稳健性进行仿真分析。设该信号的PRI值按顺序依次为PRI1,PRI2,PRI3,PRI4,PRI5和PRI6,并以此作为该信号的脉冲PRI样本序列;作为比对所截取的未知信号序列其PRI分别为X1,X2,X3,X4,X5和X6;干扰脉冲为U1和U2。

图1 六参差样本的自得分矩阵

图2 不匹配情况下的互得分矩阵
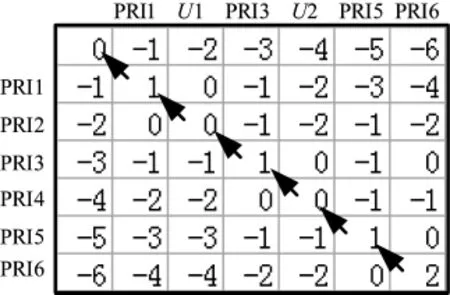
图3 存在干扰脉冲时的互得分矩阵
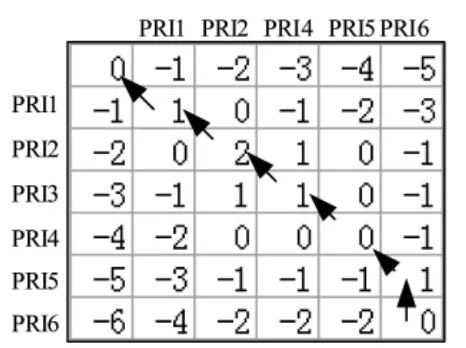
图4 存在脉冲丢失时的互得分矩阵
图1为该脉冲PRI样本的自得分矩阵,分数为21;图2为该样本与一不匹配的脉冲列形成的互得分矩阵,分数为-21,从而识别匹配度为-1;图3为存在干扰脉冲时的互得分矩阵,分数为5,从而识别匹配度约为23.8%;图4为存在脉冲丢失的互得分矩阵,识别匹配度为23.8%。
通过对大量实际侦收信号进行仿真,认为将门限取为1.5较为合适,平均识别准确率在93%以上。
3.2 PRI三编码信号的识别
设PRI三编码信号的PRI为PRI_1,PRI_2,PRI_3。对于这种信号在建立脉冲PRI样本的时候,是通过对侦收的该信号序列进行人工分析然后提取其中比较具有代表性的一小段来完成的。这里选取 PRI_1,PRI_3,PRI_3,PRI_2,PRI_1,PRI_2作为该信号的一个脉冲PRI样本序列。
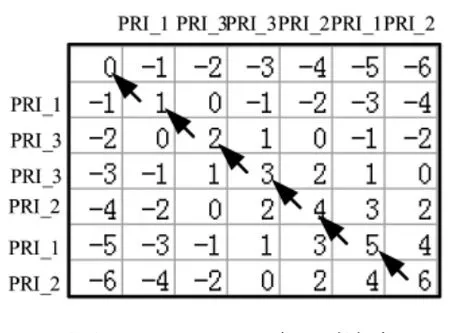
图5 PRI三编码样本的自得分矩阵
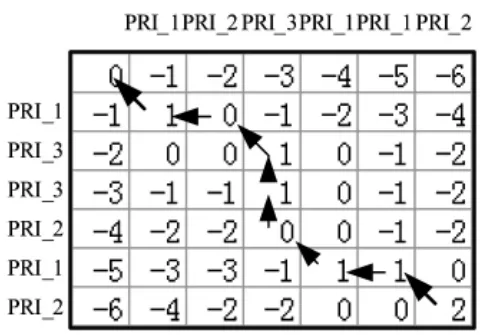
图6 PRI三编码序列的互得分矩阵
图5是该信号脉冲PRI样本的自得分矩阵,分数为21,图6是与一待识别脉冲PRI序列的一段子序列的互得分矩阵,分数为7,因此,识别匹配度约为30%。
通过利用多组实际侦收的PRI编码信号进行仿真,当门限取为1.5时,平均识别准确率可达91.2%。
4 结论
通过上面的讨论与仿真分析可以看出,该算法可以对复杂PRI样式的雷达信号进行较好的描述,并且只利用脉冲序列的PRI信息,启发式搜索PRI变化规律的相似性并将这种相似性量化成得分矩阵中各元素的分数,然后进行累加,仿真结果说明了该算法在存在脉冲丢失和干扰脉冲的情况下仍具有稳健性。
现代ESM中测时设备的精度可以做得很高,这也使脉冲序列的PRI及其变化规律能够提供更可靠的分类识别信息,相比其他一些多参数的识别算法[14-16],提取PRI的变化规律作为分类特征更具有研究潜力与应用价值。此外,可以考虑将这种方法用于对相控阵雷达复杂工作样式信号的识别。
下一步还需要进一步研究的内容主要有脉冲PRI样本在数据库中的存储与管理问题以及待识别脉冲序列的选取问题。
[1]韩俊,何明浩,李胜喜,等.现代雷达辐射源识别技术综述[J].航天电子对抗,2008,24(1):43-45.
[2]刘海军,柳征,姜文利,等.基于联合参数建模的雷达辐射源识别方法[J].宇航学报,2011,32(1):142-149.
[3]赖中安,罗杰.基于雷达辐射源识别专家系统的数据融合方法研究[J].舰船电子对抗,2012,35(3):37-39.
[4]刘凯,王杰贵,李俊武.基于区间灰关联的雷达辐射源识别新方法[J].火力与指挥控制,2013,38(1):138-141.
[5]刘海军,柳征,姜文利,等.基于云模型和矢量神经网络的辐射源识别方法[J].电子学报,2010,38(12):2798-2801.
[6]胡可,王宏远.基于粗糙集的决策树雷达辐射源识别方法[J].计算机仿真,2011,28(8):29-30.
[7]Hassan H E.A New Algorithm for Radar Emitter Recognition[C]//Proceedings of the 3rd International Symposium on Image and Signal Processing and Analysis,Ontario,2003.
[8]杨博,许丹,黄知涛,等.雷达辐射源的序贯识别方法[J].宇航学报,2008,29(3):1022-1024.
[9]Gong L L,Wu S L.A Radar Emitter Identification Method Based on Pulse Match Template Sequence[C]//2010 2nd International Conference on Signal Processing Systems,IEEE,2010.
[10]马爽,王莹桂,柳征,等.基于序列比对的多功能雷达搜索规律识别方法 [J].电子学报,2012,40(7):1435-1439.
[11]唐玉荣.生物信息学中的序列比对算法研究[D].北京:中国农业大学,2004.
[12]Richard G.Wiley.ELINT:The Interception and Analysis of Radar Signals[M].北京:电子工业出版社,2008.
[13]王晓峰.雷达信号快速分选算法研究[D].长春:空军航空大学,2011.
[14]徐欣,刁联旺,于永生.雷达辐射源类型识别分析[J].计算机与数字工程,2013,41(4):565-568.
[15]丁军,刘志成.基于特征参数匹配的雷达辐射源识别方法研究[J].现代雷达,2011,33(9):29-32.
[16]张中山,贾可新.基于量子神经网络的辐射源识别方法[J].航天电子对抗,2013,3(2):182-184.
[17]黄渊凌,郑辉,万坚.特定辐射源识别的信息论描述[J].西安电子科技大学学报,2012,39(6):125-130.
A Radar Emitter Recognition Method Based on the PRI Switching Rules
GUAN Yi-fu,ZHANG Guo-yi,WANG Xiao-feng
(Aviation University of Air Force,Changchun 130022,China)
Focusing on the problem that phased-array radar has some modes with complex PRI modulation patterns are difficult to accurately identify,this paper proposes a recognition method by extracting the switching rules of the PRI sequence.This method draws on the pulse template model and the dynamic programming theory of bioinformatics in gene sequence alignment,having solved the difficulty in describing some complex PRI modulation pattern and those for statistical methods in recognizing phased-array radars with mode includes a complete sequence of pulses with very short length.Simulation results show the effectiveness of the algorithm and its robustness even in the presence of interference pulses and missing pulses.
PRI switching rules,radar emitter,recognition
TN971
A
1002-0640(2015)03-0079-04
2014-01-11
2014-03-25
关一夫(1988- ),男,黑龙江哈尔滨人,在读研究生。研究方向:雷达信号分选和雷达辐射源识别。
