复杂系统维修性综合评估技术

张联禾

（中国飞行试验研究院，西安 710089）

复杂系统维修性综合评估技术

张联禾

（中国飞行试验研究院，西安 710089）

分析了复杂系统使用期间维修性水平动态变化特点，研究了复杂系统在使用中维修性数据特点、类型和分布确定方法，建立了复杂系统使用期间维修性指标综合评估模型，提出了维修性增长极大似然评估方法，为复杂系统维修性指标计算和评估提供参考。

维修性，数据分布，似然估计，增长评估

0 引言

随着航空科学技术的发展，航空装备系统正在向数字化、智能化发展，系统组成、功能越来越复杂，综合化程度越来越高。这样的复杂系统不但要求具有优越的性能，而且要寿命长、故障少、易于维修保障，从而使其具有较高作战使用效能和较低寿命周期费用，以获得最佳的效费比［1］。维修性是影响复杂系统作战效能和寿命周期费用的重要因素，也是影响系统质量的重要内涵。航空发达国家通过维修性工程技术的发展与应用，在复杂系统研制中获得了巨大的经济效益。进入21世纪以来，欧美各国在维修性工程技术的发展方面又取得了新进展。

在复杂系统使用期间，通过“试验-分析-改进”的方式不断发现和消除系统设计或制造过程中的薄弱环节，使系统维修性获得逐步提高，是典型的维修性增长过程。在这个过程中，如果能够准确地对其维修性进行评估，验证维修性指标的符合性并尽早发现维修性方面存在的问题，促进产品设计改进，对顺利完成系统研制，提升系统效能具有非常重要的作用。

维修性问题设计更改会导致系统维修性状态发生变化［2］。另一方面，随着系统使用维修人员的技术熟练程度也在逐步提高，维修工作流程和维修计划也在不断地优化和完善。因此，系统维修性将会处于动态变化和不断增长中。其次，从严格的统计意义上讲，统计评估的样本数据必须来自同一母体。但是，由于对发现的维修性问题采取了改进措施，系统技术状态随之发生了变化，即样本数据的母体发生了变化。最后，由于采集的维修数据来自不同维修技术状态，而且技术状态频繁更改，导致任一状态下收集的数据量有限，给传统的依赖统计方法进行评估带来困难。并且，要获得来自同一母体足够数量的样本，在时间和经费上都是不允许的。

因此，本文针对复杂系统使用期间维修性评估存在的特点，研究维修性数据分类和增长评估方法，提出了基于似然估计的维修性增长模型，建立了复杂系统维修性综合评估方法。

1 使用期间维修性数据特点及分类

目前，火控系统、雷达系统等复杂系统在使用期间，往往发生的故障较多，则其维修性数据也相对较多，而另外某些系统则故障较少，甚至只有1次～2次故障［3］，相应的维修性数据也较少。特别是通过使用还将对系统进行设计更改，样本母体发生变化，之前采集的数据一般不能直接应用于系统维修性评估。在维修性数据采集过程中，还会经常出现数据不能准确记录的情况。例如，有些故障暂时不影响系统使用安全，可能会不进行彻底地修复，此时记录的维修数据并不能代表正常情况下的维修状况，这类数据将比正常数据偏小。有些时候，某些系统处于试验状态，技术状态和维修方式尚未完全固化，此时采集到的数据将比正常数据偏大。另外，系统本身的保障条件也在不断完善，不可避免地会产生各种延误时间，如等待备件等，这样收集到的数据也将比正常数据偏大。上述几类数据都不能直接应用于维修性评估。

使用期间维修时间可以分为不完全维修时间、完全维修时间、超完全维修时间3类。具体如表1所示。

表1 使用期间维修时间分类表

因此，根据表1分类，维修时间数据也可以分为完全维修时间数据、不完全维修时间数据和超完全维修时间。所谓完全维修时间数据是指故障发生后经过了故障定位、隔离、拆卸、维修、更换、调整、检验等一系列过程的维修时间。不完全维修时间数据是指没有进行完全维修过程的情况，主要包括故障后发现不影响安全使用以及返厂修理等情况。在记录维修事件时，为处理因保障设备等因素额外耗去的维修作业时间，如备件供应、管理等造成的延误时间等均不应计入修复性维修时间。但是在实际使用期间，要精确地剔除出这些时间是困难的。当保守估计这类时间时，所记录的时间就是超完全维修时间数据。因此，记录使用期间维修性数据时，除了记录具体的时间值，还应该记录下当时的故障修复情况和维修数据类别。

当在系统维修性设计方面采取了改进措施且能够证明有效时，则系统更改后收集的数据为反映改进后真实维修性状况的数据，即为完全维修数据；而更改前的维修，相对于更改后的维修来说，付出了用于克服维修性设计缺陷额外的维修时间，因此，更改前采集的数据属于超完全维修时间数据。值得注意的是，当要评估更改前的维修性时，更改前收集的数据又属于完全维修数据了。因此，这里的完全维修和超完全维修是相对于维修性设计更改而言的。

另外，没有进行改进和无需进行更改的系统所采集到的维修数据，均属于完全维修时间数据。而那些需要进行改进但尚未实施改进的系统，所收集到的数据相对于假设实施改进后的维修性评估来说，应属于超完全维修时间。

影响使用期间维修时间分类的因素主要有两方面。一是维修过程情况，二是维修性设计更改情况。维修过程情况需在记录数据时，由数据记录员详细记录；维修性更改需要在数据分析时，查找相应技术更改资料分析确定。为了清晰准确地对采集到的数据按照上述原则分类，应首先分别从维修过程和维修性改进情况进行单项分类，然后再根据单项分类之间的逻辑关系确定数据的最终类别。

2 使用期间维修性评估

2.1 维修性指标评估

复杂系统常用的维修性指标参数是MTTR（平均修复时间）。使用期间，根据复杂系统实际发生的维修性数据样本量进行维修性指标评估。一般要求样本量不少于30。

当复杂系统使用期间发生的维修样本大于等于30时，通过对样本进行分布检验，确定其数据样本分布类型后，分别采用以下模型进行评估。

（1）数据样本服从指数分布时，MTTR按式（1）进行评估：

式中：Mct为平均修复时间评估值，h；μ为指数分布数学期望。

（2）数据样本服从正态分布时，MTTR按式（2）进行评估：

式中：Mct为平均修复时间评估值，h；μ为正态分布数学期望，h。

（3）数据样本服从对数正态分布时，MTTR按式（3）进行评估：

式中：Mct为平均修复时间评估值，h；μ为对数正态分布数学期望；σ为对数正态分布方差。

（4）数据样本服从威布尔分布时，MTTR按式（4）进行评估：

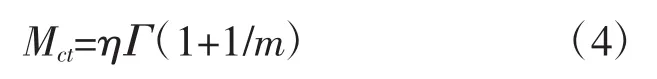
式中：Mct为平均修复时间评估值，h；η为威布尔分布数学期望；

（5）样本均不服从（1）～（4）分布情况下，MTTR按式（5）和式（6）进行评估：

式中：Mct为平均修复时间点估计值，h；T1为修复性维修总时间，h；r1为修复性维修作业次数。

对按式（5）计算出的平均修复时间评估值用式（6）进行评判：

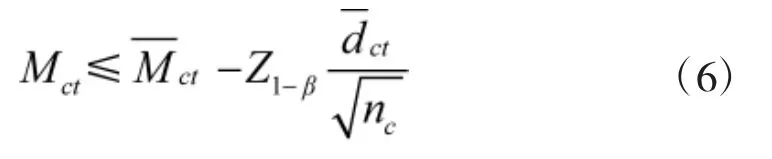
当满足上式时，则平均修复时间符合要求，否则不满足要求。

式中：Mct为平均修复时间点估计值，h；为规定的平均修复时间指标值，h；Z1-β为对应下侧概率（1—β）的标准正态分布分位数，β是订购方风险，未给定时取0.10；为修复性维修样本标准差；nc为修复性维修样本量，应大于等于30。

当复杂系统实际发生维修样本小于30时，可采用模拟试验的方法补充维修样本后再按上述方法进行评估。在进行维修性模拟试验时，系统各组成单元状态必须符合规定要求，按照各组成LRU（现场可更换单元）故障率对样本进行分配，模拟实际发生故障后排除和修复过程并记录维修数据。

维修性指标MTTR评估流程见图3所示。

3.2 维修性增长评估

3.2.1 维修性增长趋势分析

复杂系统维修性增长的主要因素是维修性设计的更改和维修熟练程度的提高。依据引起维修性增长的因素不同，维修性增长评估方法可以分为两大类。

维修性设计的更改引起维修性增长主要体现在局部增长，是在某一时间段内的增长［4］，这种情况可以利用极大似然法进行评估，所使用的样本包括改进前和改进后的维修数据。

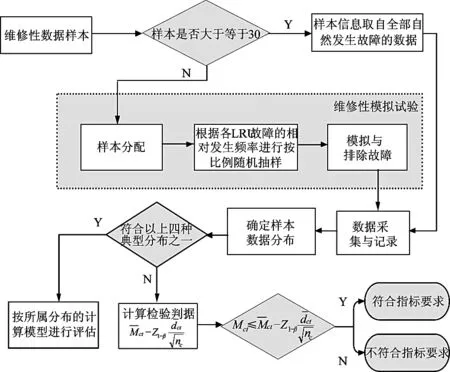
图3 维修性指标评估流程

维修熟练程度的提高、维修方案和流程的优化等因素所引起的维修性增长，则体现在整个使用阶段，是一种全局的增长。此时，维修性状态即维修性母体分布在不断变化，应该建立回归模型。

使用期间维修性增长趋势分析，首先应该对数据进行整理，剔除影响评估结果的异常值，然后利用样本数据对增长模型参数进行估计，并进行拟合优度检验，计算拟合度。当估计出的模型能够通过拟合优度检验，拟合度也符合要求时，即可进行维修性增长趋势分析和评估。对维修性进行增长分析主要思路是考察累积维修时间与维修次数之间的关系，将各次维修时间进行累加，并绘制出累计维修时间的增长曲线，寻找增长规律。它所评估的是维修性增长的总体趋势，这种总体趋势中包含了局部增长和设计改进等综合因素的影响，也有可能出现负增长等情况，但暂时的波动不会对总体的趋势带来太剧烈的影响。

维修性增长趋势分析步骤主要包括：①数据预处理：剔除异常值，对维修时间进行累加；②模型参数估计：根据所获得的数据估计模型参数；③拟合优度检验：可采用F检验法根据已获数据来判断增长是否符合增长模型；④计算拟合度：拟合度是一个取值在0到1之间的数，该值越大说明拟合程度越好；⑤对维修性指标进行评估。

3.2.2 维修性增长似然估计

在使用期间，若需评估复杂系统某次改进后的维修性指标时，则将改进后的维修时间视为随机变量X。对于A、B、C 3类维修性数据，发生了3种概率事件：

当样本数据属于“完全维修”时，发生了事件“X=xi”；当样本数据属于“不完全维修”时，发生了事件“X＞xi”；当样本数据属于“超完全维修”时，发生了事件“X＜xi”。

传统的评估方法，只有属于事件“X=xi”的数据才能用来估计随机变量X的分布参数。当此类数据达不到一定量的样本需求时，估计出的分布参数将有较大的偏差。为了扩充样本量，有效充分地利用其他两类数据，本文采用极大似然法来解决这一问题。

假设A、B、C 3类维修性数据样本出现的概率分别为：

（1）A类“完全维修”数据的概率为P（X=xi）；

（2）B类“不完全维修”数据的概率为P（X＞xi）；

（3）C类“超完全维修”数据的概率为P（X＜xi）。

若维修性数据样本个数为n，3类样本数据个数分别为r、s-r、n-s，则可构建似然函数：

可以看出，新建立的似然函数不但使用了改进后的数据，还使用了改进前的数据，并且利用了异常数据。这样有效地挖掘了样本潜在信息，扩充了样本量。

假设维修数据服从对数正态分布。设改进后维修时间X取对数后的分布密度是

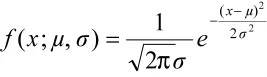
其中（x1，x2，…，xn）为取对数后的维修时间，在本文后面的叙述中，不加说明的认为样本值均为取对数后的值。μ，σ是未知参数，μ=E（1nti）表示各单次维修时间的数学期望，σ是其标准差。因此，

这里取的小区间长度dxi是固定量。选择μ，σ的值使P（X=xi）达到最大，亦即使f（xi；μ，σ）达到最大。因此，似然函数为：

其中：

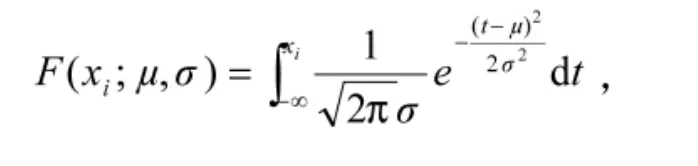
选择μ，σ使达到L最大，即

令：

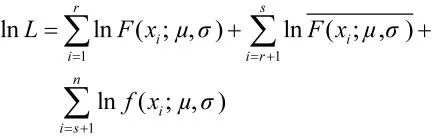
对1nL中的μ、σ求偏导，并令偏导数等于零，得：

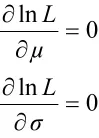
分别将3类数据代入极大似然函数的3个部分，即可求解分布参数。其中，“C类”数据代入P（X＜xi）部分，“B类”数据代入P（X=xi）部分，“A类”数据代入P（X＞xi）部分。

求解整个方程组这样得到的μ，σ的值作为相应未知参数的估计值，再根据式（3）便可得到平均修复时间MTTR。

4 结论

传统的复杂系统使用期间维修性指标评估方法仅能使用“完全时间”类数据进行评估，这就使得可用的样本大大减少。当样本量不足时，样本不能遍历整个样本空间，不能准确地对复杂系统维修性进行评估。本文提出将复杂系统维修性数据分为“完全时间”、“不完全时间”和“超完全时间”3类，并根据维修性数据的分类特点，重新构建了求解分布参数的极大似然函数，充分利用已有的数据进行维修性增长评估，建立了复杂系统维修性指标综合评估方法，使得维修性指标评估更加科学合理，工程上具有很好的应用性。

［1］陈学楚，张诤敏，陈云翔，梁工谦，陈翔宇.装备系统工程［M］.北京：国防工业出版社，2005.

［2］张会奇.维修性对装备维修工作量的影响分析［J］.装甲兵工程学院学报，2008，36（5）：74-78.

［3］杨晋.机载火控系统故障［J］.计算机测量与控制，2009，54（8）：56-59.

［4］廖武.维修性增长指标分配方案的决策与优选［J］.电光与控制，2010，32（10）：32-35.

Complex System Maintainability Integrated Evaluation Technique

ZHANG Lian-he
（China Flight Test Estabishment，Xi’an 710089，China）

This paper analyzes the maintainability dynamic characteristics of the complex systems during the using period，studies the maintainability characteritics，types and distribution determining method，comprehensive maintainability index evaluation model，puts forward the maximum likelihood estimation method of maintainability growth，provides a reference of maintainability index calculation and evaluation for complex system.

maintainability，data distribution，likelihood estimation，growth assessment

V37

A

1002-0640（2015）03-0163-04

2014-01-26

2014-03-19

张联禾（1970- ），男，陕西户县人，硕士，高级工程师。研究方向：航空装备可靠性维修性。