基于中心凸包算法与增量学习的SVM算法研究*

白东颖，王 刚，张 泚

（1.第二炮兵工程大学，西安 710025；2.空军工程大学防空反导学院，西安 710051；3.解放军94402部队，济南 250002）

基于中心凸包算法与增量学习的SVM算法研究*

白东颖1，2，王 刚2，张 泚3

（1.第二炮兵工程大学，西安 710025；2.空军工程大学防空反导学院，西安 710051；3.解放军94402部队，济南 250002）

基于计算几何理论，在分析支持向量与凸包向量关系的基础上，提出了一种基于中心凸包算法与增量学习的SVM学习算法。在确保分类器达到可靠精度的前提下，为解决学习中时耗过长的问题，在对当前训练集计算凸包的基础上采用欧式中心距离淘汰法对训练样本进一步精简，并且每次进行增量学习的样本都包含前次训练样本集中违背KKT条件的样本，在UCI数据库上进行算法对比实验，结果表明算法的可行性和有效性。

凸包，增量支持向量机，中心距离，KKT

0 引言

支持向量机［1］（Support Vector Machine，SVM）是一种以统计学习理论为基础的机器学习技术，主要应用于求解监督学习［2］问题。在实际应用中，训练样本常常具有在线式增加的特点，这就要求分类器不断地对新样本重新训练，使得分类效率大大降低，而增量学习旨在获得原训练样本与新增样本并集的最优解，因此，对于不断增长的数据集来说，支持向量机增量学习具有其独特的优势。

当前，对增量SVM算法的研究主要集中在如何保证分类精度与提高学习速度两个方面。见文献［3-12］。

由以上分析可知，如何对训练样本有效淘汰在一定程度上影响了SVM分类精度与学习速度。本文分析了计算几何［13］中构成凸包的向量与支持向量之间的关系，采用了凸包算法与样本的欧氏中心距离［14］概念结合进行样本筛选，依据KKT条件更新增量训练样本，提出了一种利用中心凸包算法与增量学习的SVM快速学习算法，简称CQSVM。

1 SVM分类原理及支持向量与凸包向量的几何关系

1.1 SVM分类原理

SVM是从线性最优分类超平面发展而来，最优分类面问题可以表示成如下的约束优化问题［1］：

定义Lagrange函数为：

则原问题在原约束条件下可以转化为如下凸二次规划的对偶问题：

上述方程其实质是一个不等式约束下的二次函数机制问题，存在唯一最优解αi*，则：

αi*不为零时，所得到的样本为支持向量。因此，最优分类面中所采用的权系数向量是支持向量的线性组合，b*可通过约束条件求解，由此得到的最优分类函数是：

1.2 支持向量和凸包向量的几何关系

文献［15］指出：寻找使2类间的分类边界最大的最优超平面等同于在2类数据相应的凸包上寻找2个最近邻点。2类线性可分样本最优分类面的几何意义见图1所示。

在线性可分的情况下，是由SV来确定SVM最优分类面的位置。为确保最优分类面能够最大化2类样本间的最小间隙，SV只可能在位于2类样本集合边界位置的样本向量中产生。

凸包是指每一类训练集几何意义上最边缘的样本［13］。SVM算法旨在寻求两个凸集之间的最小距离最大化，SV一定出现在样本集合的最边缘位置。可以说，SV产生于样本集的凸包上以及凸包周围。当SV确定后，最优分类面的位置也就得到了确定。

第三，完善资本市场机制。完善绿色金融市场相关规定，优化证券发行和准入机制，降低绿色债券发行成本、拓宽发行渠道，扩大绿色债券发行对生态产业的正效益，使企业直接融资更加容易，最终做到提高绿色金融支持效率。

2 KKT条件及支持向量变化情况分析

KKT条件（Karush-Kuhn-Tucher condition）［1］在约束优化中具有重要作用。根据KKT条件，在最优点，拉格朗日乘子与约束的积为0。取线性判别函数：

则对偶问题的最优解α=［α1，α2，…，αl］使得每个样本x满足优化问题的KKT条件为：

式中，非零的αi为SV。考虑函数系g（x）=h，可知g（x）=0为分类面，g（x）=±1为分类间隔的边界，其上的样本即为SV。

定理1新增样本加入后，一部分与KKT条件相违背的新增样本将转化为满足KKT条件的样本甚至SV；部分满足KKT条件的新增样本将转化为SV；部分满足KKT条件的原样本集的非SV将转化为SV；部分原SV将转化为非SV。这就意味着，标准增量训练过程中，仅考虑新增样本和原样本集的SV集，而忽略原样本集中的非SV集可能造成重要信息的丢失。因此，每次进行增量训练时，训练样本还应包含上次训练样本集中违背KKT条件的样本。

3 基于中心凸包与增量学习的SVM算法

3.1 算法原理

为保证包含分类信息的训练样本在筛选时被有效保留，同时考虑到原SV集可能受到新增样本集的影响，在进行新的增量学习过程中，将前次训练过程中与KKT条件相违背的样本同本次新增样本点一起作为当前训练样本集。同时，在对当前训练集计算凸包的基础上进行训练样本集筛选，采用欧式中心距离淘汰法将边界凸包向量提取出来，作为增量SVM训练的训练集。

3.2 算法描述

3.2.1 符号说明

3.2.2 算法步骤

（1）对Qhull{X0}训练得到分类器Ω0。

（2）第k次增量学习（k=1，2，…，n）时，算法描述为：步骤1检验增量过程是否继续，如果不继续，转步骤3，否则，执行步骤2；步骤2求Xk-1的中心凸包向量CQhull{Xk-1}；步骤3计算Xk-1中违背KKT条件的样本；步骤4令Xk=Ik+CQhull{Xk-1}+；步骤5用Xk训练获得分类器Ωk。

（3）终止，输出Ωk。

4 实验分析

4.1 实验数据及参数设置

实验环境为Intel酷睿2.50 GHz，内存2 GB的PC机，Matlab7.0平台，采用libsvm-mat-2.91-1的工具包。为验证算法的有效性，选取UCI数据库中2类不同的数据进行学习：①Breast-cancer数据集，选取训练样本为300，测试样本为300；②Artificial数据集，取训练样本为600，测试样本数为300，样本类别数为2，2类中心欧式距离为3。

4.2 相关对比算法

方法1：IncHulSVM0（）。只采用凸包算法进行训练集约简；每次增量学习过程中，用本次计算的凸包向量与新增样本一起求解分类器。

方法2：IncHulSVM1（）。只采用凸包算法进行训练集约简；每次增量学习过程中，用本次计算的凸包向量和前次训练样本集中违背广义KKT条件的样本以及新增样本点一起进行分类器的求解。

方法3：IncHulCntr0（）。采用中心凸包算子进行样本约简；每次进行增量学习时，仅用本次计算的中心凸包向量与新增样本点求解分类器。

方法4：标准增量SVM，记为SISVM。

4.3 实验结果与分析

图2和图3是在Breast-cancer数据集上的实验结果。图4和图5是基于Aritificial数据集的测试结果。实验选用RBF核函数来确定训练时间，而分类精度是在不同核函数（Linear、Rbf）下求得的分类精度的平均值。

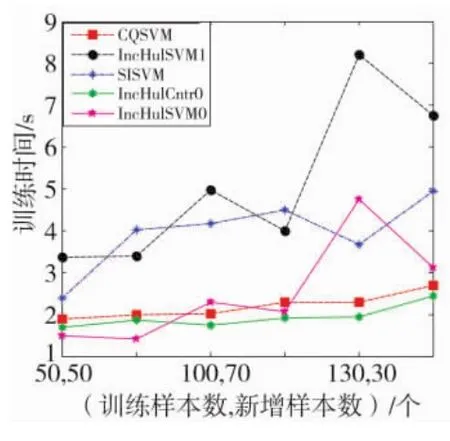
图2 Breast-cancer数据集下本文算法与对比算法训练时间比较图

图3 Breast-cancer数据集下本文算法与对比算法学习精度比较图

图4 Artificial数据集下本文算法与对比算法训练时间比较图

图5 Artificial数据集下本文算法与对比算法学习精度比较图

对以上实验结果分析：①从训练时间上来说，对于Breast-cancer数据集，训练样本数为300。由图2可见，IncHulSVM0、IncHulCntr0与CQSVM训练时间较短，SISVM及IncHulSVM1耗时较长，由于选取的训练样本集规模不大，因此，上述几种方法在训练时间上都有不同程度的重叠，不能确定何种方式的训练速度最快。而对于Artificial数据集，训练样本数为600，规模较大。由图4可见，这些方法中，按时耗由小到大排序分别是：IncHulSVM0、IncHulCntr0、CQSVM、IncHulSVM1、SISVM；②从分类精度上来说，图3与图5表明，不管采用Artificial或者Breast-cancer数据集，CQSVM与SISVM的分类精度是最高的，并且两者的分类精度近似。方法IncHulSVM0虽然耗时最短，但其分类精度也最低。方法IncHulCntr0与IncHulSVM1体现出近似性能，均高于方法 IncHulSVM0，但低于 CQSVM与SISVM。

CQSVM算法核心思想是提高SVM增量学习速度的同时尽量不降低分类精度。从训练时间的角度分析，在采用了凸包算法对训练样本约简后进一步用中心距离比值来简化训练样本，提高训练速度；从分类精度方面来说，每次进行增量训练的样本都包含了前次训练样本集中与广义KKT条件相违背的样本，体现了对新增样本的合理利用，使得分类精度尽量不降低。

5 结束语

利用KKT条件，着重对SV集受到新增样本的影响进行了分析；从计算几何角度指出寻找使2类间的分类边际最大的最优超平面等同于在两类数据相应的的凸包上寻找2个最近邻点。提出了基于中心凸包算法与增量学习的SVM算法，该方法结合了凸包算法与中心距离淘汰法，同时每次进行增量学习的样本中都包含了前次训练样本集中与KKT条件相违背的样本。实验表明，该算法能够在保持较高分类精度的同时大大提高SVM增量学习的速度。

［1］Vapnik V.The Nature of Statistical Learning Theory［M］.New York：Springer Verlag，1995.

［2］王珏，周志华，周傲英.机器学习及其应用［M］.北京:清华大学出版社，2006.

［3］Syed N，Liu H，Sung K.Incremental Learning with Support Vector Machines.［C］//Proceedings of the Workshop on SupportVector Machines atthe InternationalJoint Conference on Artificial Intelligence.Stockholm ，Sweden: Morgan Kaufmann，1999.

［4］文波，单甘霖，段修生.基于驱动错误准则的SVM增量学习研究［J］.计算机技术与自动化，2012，31（3）:100-103.

［5］吴崇明，王晓丹，白冬婴.基于类边界壳向量的快速SVM增量学习算法［J］.计算机工程与应用，2010，46（23）: 185-187.

［6］ RalaivolaL，dAlch-BucF.IncrementalSupportVector Machine Learning:A Local Approach［C］//Proc.of ICANN，01.Vienna，Austria:Springer，2001.

［7］牟琦，陈艺坤，毕孝儒.一种基于快速增量SVM的入侵检测方法［J］.计算机工程，2012，38（12）:92-94.

［8］毛建洋，黄道.一种新的支持向量机增量算法［J］.华东理工大学学报（自然科学版），2006（8）:989-991.

［9］李忠伟，张健沛，杨静.基于支持向量机的增量学习算法研究［J］.哈尔滨工程大学学报，2005，26（5）:643-646.

［10］王一，杨俊安，刘辉.一种基于内壳向量的SVM增量式学习算法［J］.电路与系统学报，2011，16（6）:109-113.

［11］ Gert C，Tomaso P.Incremental and Decremental Support VectorMachine Learning ［C］//Adancesin Neural Information Processing Systems（NIPS*2000）.Cambridge，MA:MIT Press，2001.

［12］申丰山，张军英，王开军.使用模拟切削算法的SVM增量学习机制［J］.模式识别与人工智能，2010，23（4）: 491-500.

［13］周培德.计算几何—算法分析与设计［M］.北京:清华大学出版社，2003.

［14］Zhang L，Zhou W D，Jiao L C.Pre-extracting Support Vectors for Support Vector Machine［C］//Proceeding of ICSP2000.Beijing:IEEE Press，2000.

［15］Theodorids S，Koutroumbas K.Pattern Recognition，Third Edition［M］.Beijing:China Machine Press，2006.

Study on SVM Algorithm using Center Convex Vector and Incremental Learning

BAI Dong-ying1，2，WANG Gang2，ZHANG Ci3
（1.The Second Artillery Engineering University，Xi’an 710025，China；
2.Air and Missile Defense College，Air Force Engineering University，Xi’an 710051，China；
3.Unit 94402 of PLA，Jinan 250002，China）

Based on analysis of the support vector geometry significance and convex vector relationship，a learning algorithm of fast incremental convex vector algorithm based on SVM is proposed.In order to enhance training speed while SVM incremental learning accuracy is ensured，the training set is acquired based on computing the convex vector of the center distance method in the training sample set，and each incremental training sample contains the last training sample set against the KKT conditions of the sample，various algorithms then are used for comparison experiment under the UCI standard database，the result shows the feasibility and validity of this algorithm.

convex hull，incremental support vector machine，center distance，Karush-Kuhn-Tucher

TP18

A

1002-0640（2015）03-0020-04

2014-01-15

2014-03-27

国家自然科学基金资助项目（61102109）

白东颖（1982- ），女，陕西宝鸡人，博士。研究方向：智能信息处理。