压印接头强度的有限元模型及理论计算方法

杨慧艳，何晓聪，周 森

(昆明理工大学 机电工程学院，昆明650500)

0 引 言

随着汽车工业的迅速发展和日趋激烈的竞争，轻量化结构和新轻型材料逐渐得到重视和发展。铝、镁合金等材料在汽车、家电等领域应用越来越多，但由于这些材料化学或物理性能导致焊接性能不好或根本无法焊接，而且点焊很难实现异种板材组合、多层板材组合、有夹层等连接。因此，急需开发新的板料连接技术，压印连接是近年来快速发展起来的薄板连接新技术。压印连接技术由专用的压印连接模具在外力作用下，迫使被连接材料组合在连接点处产生材料流动，通过金属塑性变形形成一个相互镶嵌的内锁机构。

在连接强度上，压印单点静拉伸强度是点焊拉伸强度的70%，双点连接强度与点焊的相等［1-2］。要将压印连接技术应用于汽车车身中，压印接头强度研究很重要。压印连接技术诞生至今，国内外许多学者对其进行了多方面的研究，并产生了一系列成果。何晓聪从工艺参数、接头强度、振动特性等方面综述了压印连接技术的发展状况［3-4］。De Paula［5］研究了模具几何尺寸以及压印连接过程中诸如冲压力等参数对连接接头强度的影响。Varis［6-7］研究了模具尺寸、板料厚度等对接头成形的影响。周云郊等［8］采用试验和有限元模拟相结合的方法对钢-铝组合板材的压印连接件进行了几何工艺参数的多目标优化。黄柳钧等［9］研究了模具参数对接头失效形式、断面质量和剪切强度的影响规律。从国内外的公开文献看，压印连接技术的大部分研究主要集中于几何参数及接头强度研究上，且研究方法大多局限于试验。龙江启等［10］基于神经网络提出了压印接头力学性能预测的方法。Lee［11］提出了固定模压印接头的强度预测方法。而这些压印接头强度的预测方法中均对接头形状进行了近似处理。压印连接的下模具有固定模和分瓣模两种，分瓣模得到的压印连接点更可靠，固定模得到的压印点形状和成形过程相对简单。在压印连接的相关研究和实际应用中大多采用分瓣模压印点，涉及到有限元建模和强度计算则通过采用固定模连接点近似求解，导致求解结果与实际有较大的偏差。

本文将建立压印接头拉伸-剪切过程的有限元模型，研究接头破坏过程及接头拉剪强度。并根据接头的拉剪失效形式提出接头强度的理论计算方法。

1 压印接头拉剪强度的数值模拟

1.1 压印连接试验

所用材料为Al5052，厚度为2.0 mm，材料化学成分和机械性能参数如表1 和表2 所示，图1为材料的真实应力-应变曲线。本文用于制作试件的板料方向均沿轧制方向。

表1 Al5052 化学成分(质量分数，%)Table 1 Chemical composition of Al5052(percentage，%)

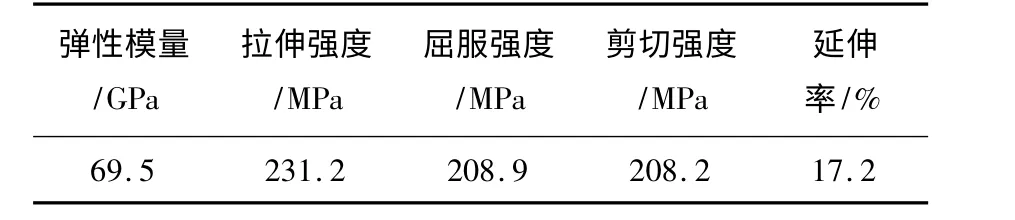
表2 Al5052 力学性能参数Table 2 Mechanical property of Al5052

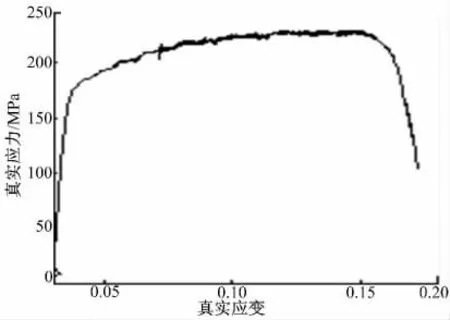
图1 Al5052 真实应力-应变曲线Fig.1 True stress-strain relationship for Al5052

压印连接试验在RIVCLINCH 1106 P50 压印连接设备上完成，选用模具为:上模型号为SR5010，下模型号为SR60314。连接件尺寸示意图如图2 所示，上、下板料尺寸为100 mm×20 mm×2 mm，搭接长度为20 mm，在搭接部位的中心进行压印连接。设备工作时的压强设定为0.6 MPa，相当于50 kN。在相同试验条件下，冲压6个试件，分别标记为Al5052-2.0+2.0-01 ～Al5052-2.0+2.0-0.6。

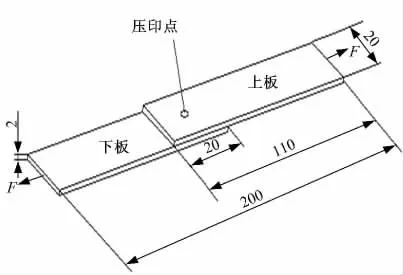
图2 压印连接件尺寸示意图Fig.2 Schematic diagram of clinched joint

取编号为Al5052-2.0+2.0-01 的试件，沿子午面将接头剖开，对压印接头显微组织形态进行特征分析。采用阳极化覆膜处理试件，用微分干涉相衬法(DIC)进行观察并通过微分干涉进行反差增强。对接头截面进行机械抛光、电解抛光、阳极化覆膜后，在智能数字万能材料显微镜上，偏光下进行微观组织分析并采集照片。电解抛光液是10 ml 体积分数为70%的高氯酸与90 ml 无水乙醇的混合液;覆膜液为5 g 氟硼酸与200 ml 水的混合液;试件作为阳极，阴极为铅块。

1.2 接头拉剪试验

试验在MTS landmark 力学试验机上完成，试件受测时在两端装加相应厚度的垫片以减小弯矩，拉伸速率设为5 mm/min。

图3 为接头的载荷-位移曲线拉剪破坏过程。5 个试件的最大拉剪载荷均值Fa=1856.0 N，标准差为43.8 N，经检验接头强度服从正态分布。

图3 拉剪试验结果Fig.3 Result of tensile-shear test

1.3 压印连接过程的有限元模型

1.3.1 有限元模型建立

采用有限元分析方法模拟压印接头的成形过程及接头拉剪过程。首先在ANSYS/LS-DYNA 中建立压印连接模型，由于压印接头几何形状轴对称，采用二维模型进行简化。压印成形模型包括:冲头、压边圈、固定下模、分瓣模、弹性体、上板料和下板料。将压边圈、冲头、固定下模、分瓣模定义为刚体，上、下板料定义为多线性弹塑性材料模型，弹簧定义成弹性体，模型示意图如图4 所示。模型尺寸与板料和设备实际尺寸一致。

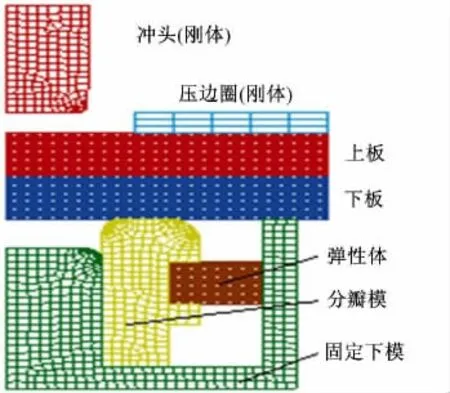
图4 压印连接过程的有限元模型Fig.4 Numerical model of riveting process

动态接触算法采用程序默认的对称罚函数法，模型各Part 间采用单面自动接触，摩擦因数设为0.15。加入自适应网格划分以避免网格严重畸变或丢失，同时，采用沙漏及积分控制、质量缩放。并按试验条件设置边界条件。

1.3.2 数值模拟结果

通过数值模拟分析可以得到金属板材的压印连接过程和接头截面。图5 为压印连接过程的模拟结果。压印连接过程分为3 个阶段显示，上、下板料随冲头下行，同时分瓣模向周围扩张，板料在下模腔内充分变形，最终形成一个固定摩擦连接点。图5(b)表明模拟结果与试验结果接近。

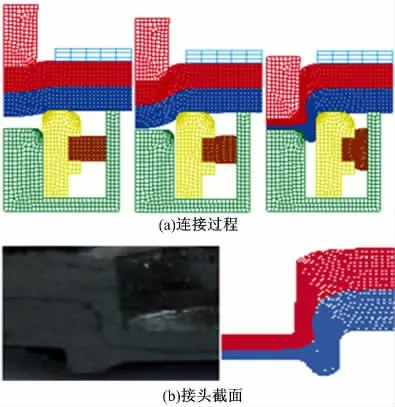
图5 压印连接过程的模拟结果Fig.5 Simulations of clinching process

图6 压印接头组织流向图Fig.6 Macrostructure diagram of clinched joints

图6 (a)为通过对处理过的压印接头截面进行电化学腐蚀，在显微镜下观察接头截面的不同区域的组织变化。在压印连接的过程中，铝合金基体金属的形状和沿晶界分布的杂质形状都要发生变形，它们将沿着变形方向被拉长，呈纤维状的流线型。从A 处的分布可以看出，距离板料和冲头接触区域越近处的晶粒变形越大，各晶粒发生定向延伸和弯曲，距离板料和冲头接触位置最近处晶粒变形最大，随着冲头冲压过程的进行，变形晶粒逐渐被拉伸成纤维状。位置B、C、D 的分布显示了晶粒在下模具作用下的变形，组织流向体现出与模具几何形状的一致性。从整个接头截面的微观组织来看，板料被拉伸成纤维状，被拉长的晶粒变形平滑，几乎不存在晶粒断裂。晶粒被拉长并细化，晶粒越来越细，晶界也越来越多，因此金属的变形越分散，减少了应力集中。有限元模型不能完全一致地描述金属内部的微观组织分布，但可通过正方形单元的变形预测金属组织流向，图6(b)为组织流向的模拟结果，模拟结果的组织流向与试验结果基本一致。

1.4 压印接头强度的有限元模型

接头三维模型由成形模拟获得的二维接头经过一系列布尔运算生成。接头强度模型建立过程如图7 所示，其中图7(a)为1.3 节中压印连接过程的数值模拟结果，由(a)经过旋转、分割得到接头部分(b);同时，在同一坐标中按照实际尺寸建立连接件的其余部分:建立相互搭接的上下两板，采用与(b)尺寸相等的圆在搭接中心进行材料切除，得到接头部分(c);将(b)与(c)相加就得到压印连接件的模型(d)。

接头拉剪强度的模拟在ANSYS 基础模块中进行，材料做非线性和接触非线性考虑。材料模型选用双线性(Biliner);接触类型选用面－面间的柔体接触;接触算法采用罚函数法。边界条件的设置与试验条件一致。

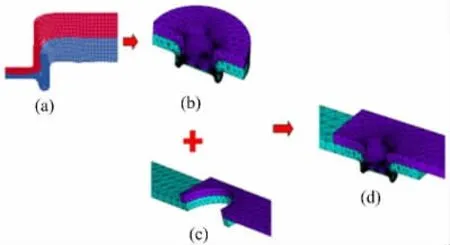
图7 接头强度模型的建立过程Fig.7 Establishment of the joint strength model

图8 压印接头强度的数值模拟结果Fig.8 Simulations of clinched joint strength

模拟结果如图8 所示，试验获得压印接头最大强度均值为1856.0 N，模拟值为1919.5 N，误差为3.4%，拉伸过程位移为0.85 mm，载荷-位移曲线形状与试验基本一致。从图8(b)可以看出:随着拉伸位移的增加，接头颈部最薄的位置出现环向的最大应力分布，且在上端应力集中现象最明显，颈部不断被拉长，上下板之间沿接头方向的缝隙不断增大，接头不断倾斜。随着上板颈部不断被拉长，颈部径向尺寸不断减小，出现屈服现象，并发生严重的塑性变形，由此可推断最终在颈部发生断裂。接头失效过程与图3(b)基本一致。

2 接头强度理论计算方法

在拉伸-剪切载荷的作用下，压印接头一般有两种失效形式:颈部断裂失效和上下板分离失效［8-9，11］。建立的压印接头强度模型可对接头强度和载荷-位移曲线进行较好的预测，但由于有限元软件的计算能力有限，尚不能预测接头上下板拉脱失效的接头强度，而且不能直观地模拟颈部断裂的现象。因此，将根据压印接头的两种失效形式提出可直接计算接头强度和失效形式的解析计算方法。

2.1 颈部断裂失效形式

单搭压印接头在拉伸-剪切载荷的作用下，随着拉伸位移的增加，施加载荷逐渐增大，接头上的应力不断增大。由图8 可以看出:接头颈部应力最大，当接头颈部应力达到材料的最大剪切应力时，颈部断裂，接头失效。压印接头的失效形式如图9(a)所示，断裂面示意图如图9(b)所示。

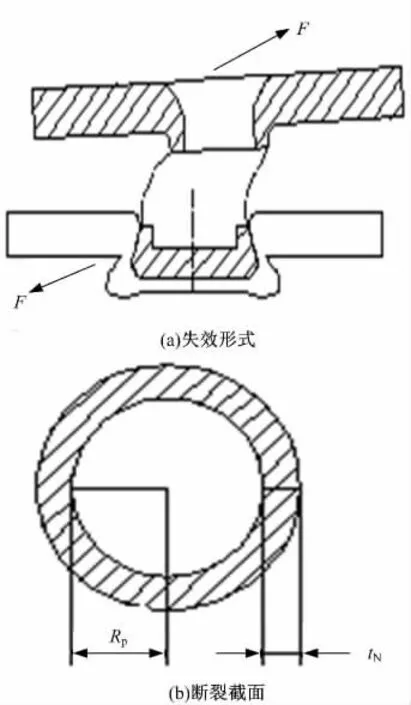
图9 颈部断裂失效形式Fig.9 Neck-fracture

颈部断裂失效属于剪切失效，断裂面近似为平面，接头破坏强度即为上板颈部剪切强度，由剪切断裂面的面积A 决定。因此，颈部断裂失效时的破坏力FN可由式(1)得到:

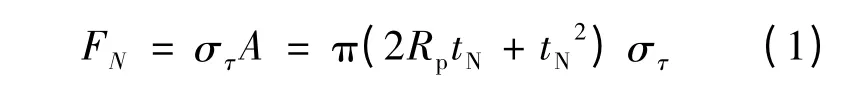
式中:στ为上板材料的剪切强度;tN为接头颈部厚度;Rp为冲头半径。

对于颈部断裂失效的压印接头，上板剪切强度、冲头半径和颈部厚度越大，接头强度越大。对于材料和厚度一定的组合接头，接头强度取决于接头颈部厚度，颈部厚度越大，接头强度越高。

2.2 上下板拉脱失效形式

上下板拉脱失效是由于接头中镶嵌量tU不足导致的。上板从下板中拉脱的过程中，右端内锁部位的材料不断发生塑性变形，直到右端镶嵌部分变平滑，接头上板从下板中拉出，接头失效。上下板失效形式如图10 所示。

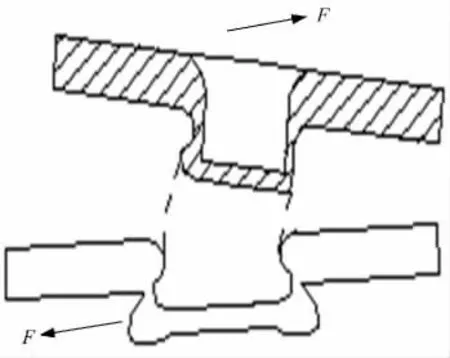
图10 上下板拉脱失效形式Fig.10 Button separation

接头强度取决于塑性变形力，金属塑性变形力的计算本身就较复杂，对于非轴对称变形的拉脱失效接头有一定难度。为简化计算、提高工程适用性，将压印接头形状进行简化，采用主应力法进行计算。简化后的接头形状和应力状态如图11 所示，由图可以看出:接头拉伸过程中的塑性变形类似于管材拉拔过程，因此压印接头强度采用管材拉拔时的拉伸力计算曲线(见图12)进行计算［12］。

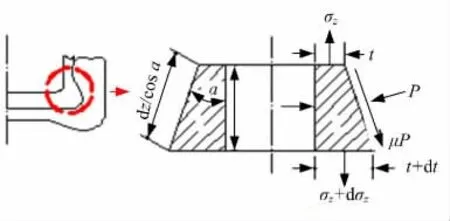
图11 接头形状简化后的应力状态Fig.11 Clinched joint section and stress condition

压印接头上下板拉脱失效形式下的接头强度计算公式为:

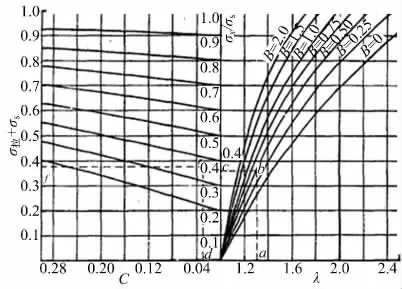
图12 拉伸力计算曲线Fig.12 Calculation curve of tension

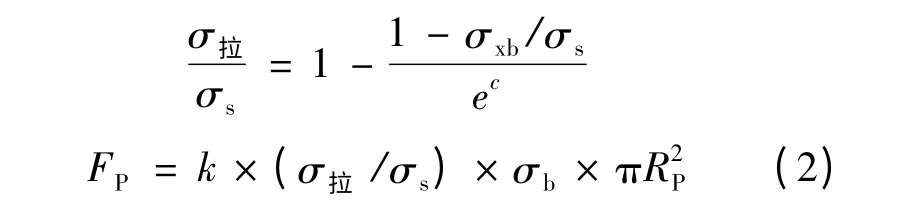
具体计算过程如下:

(1)计算拉剪过程中的延伸系数

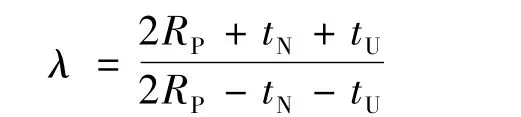
(2)根据摩擦因数μ 和倾角α 计算系数

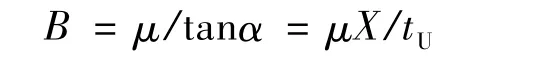
(3)根据参数λ 和B，从图12 中查到σxb/σs值。具体方法是在横坐标轴上找到λ 位置，作垂线与B 值曲线相交，从交点做水平线，与纵坐标轴的交点即为σxb/σs值。

(4)计算系数

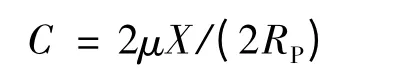
并在图12 左半部分横坐标轴上找到相应位置，过该点作垂线，与图中的σxb/σs值作为起点的曲线相交(若图中没有σxb/σs计算值的曲线，采用插入法确定交点)，交点纵坐标即为σ拉/σs值。

(5)计算拉伸过程中的加工硬化程度

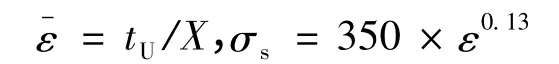
(6)计算流动应力σs值［13］

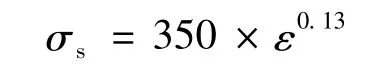
(7)由于压印接头拉脱时，部分接头发生塑性变形，式(2)中的k 值小于1，对于压印接头取k=0.8。k 值可根据接头形状进行修正。

图12 中参数的查找过程可以用a、b、c、d、e、f等点依次描述。确定这些参数之后，根据方程(2)可求得上下板分离失效模式下压印接头的强度。式中k 根据压印接头形状确定，由求解过程可知，接头强度与摩擦因数μ、底部厚度X、颈部厚度tN、镶嵌量tU、流动应力σs有关。给定板材材料和总组合厚度，摩擦因数μ、底部厚度、流动应力σs则为已知，此时接头强度取决于颈部厚度tN和镶嵌量tU，两者之和越大，接头强度越大，其中镶嵌量tU对强度的影响较颈部厚度tN大。

2.3 试验验证

压印接头颈部断裂失效形式的接头强度取决于颈部厚度tN，tN越大则接头强度越大。上下板拉脱失效的接头强度取决于颈部厚度tN和镶嵌量tU，两者之和越大则接头强度越大，其中tN的影响较tU明显。为了验证本文提出的两个接头强度计算公式，采用厚度为2.0 mm 的Al5052 进行检验。

首先对2.2 节中的颈部断裂失效接头进行检验，测量经拉剪后颈部断裂失效的1 组6 个试件的颈部厚度值，其颈部厚度均值为0.487 mm，由式(1)计算得接头强度FN=1810.6 N，试验值Fa=1856.0 N，求解误差为2.4%。

为了同时检验接头强度计算公式(1)和(2)，对2.0 mm 的Al5052，在不同的模具组合下连接，获得具有不同颈部厚度和镶嵌量的压印接头。试验共研究了12 种压印接头，颈部厚度变化范围为0.35 ～0.60 mm、镶嵌量变化范围为0.04 ～0.45 mm，如表3 所示。

表3 压印接头Table 3 clinched joints

根据12 种压印接头的颈部厚度tN和镶嵌量tU，分别按照式(1)和式(2)计算接头颈部断裂强度和上、下板拉脱失效的接头强度，取较小强度和对应的失效形式作为接头的计算强度和失效形式。

对比12 组试件的接头强度的试验结果和计算结果，如表4 所示。接头的计算预测结果与试验结果的最大误差为8.9%，计算误差较小。12种压印接头的失效形式与试验结果一致，其中12组试件中有9 组发生颈部断裂失效，其余为上下板拉脱失效。因此，本文提出的接头强度计算方法可以很好地计算和预测压印接头强度及失效形式。

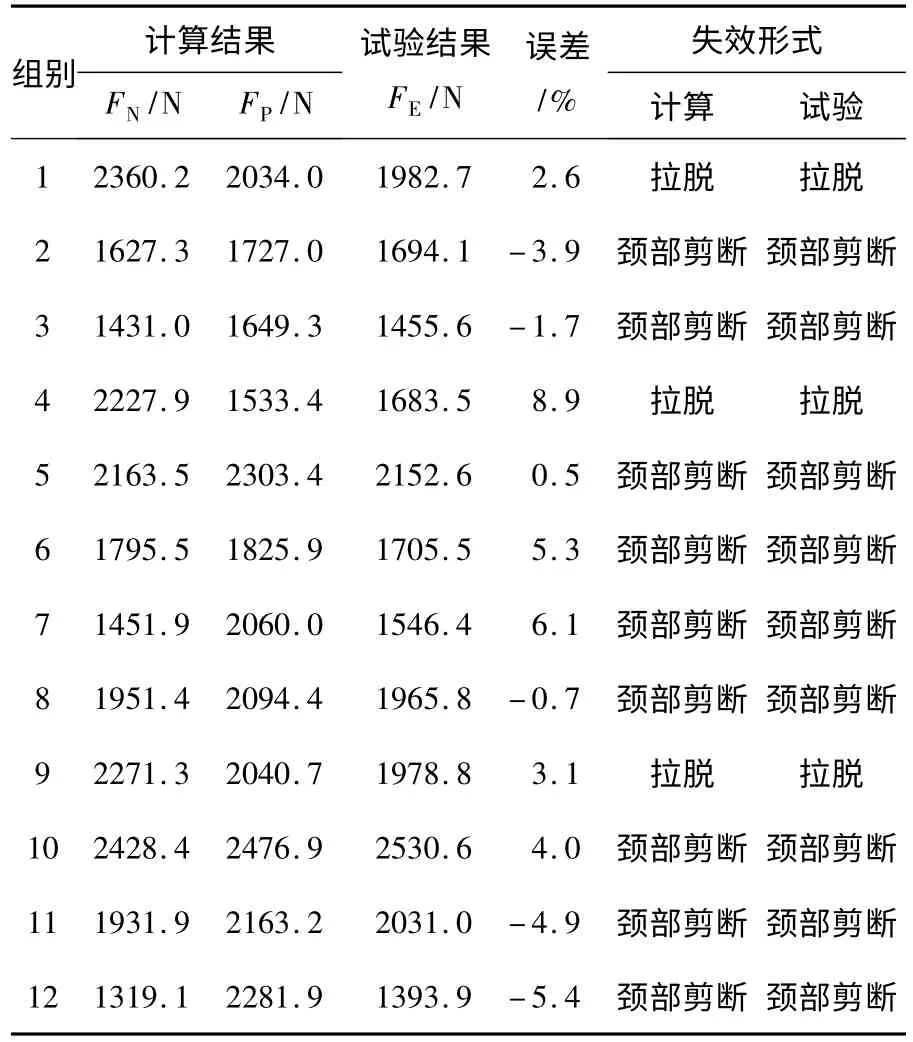
表4 接头强度预测结果和试验结果的对比Table 4 Comparison of analytical model and experiment

图13 和图14 分别为拉伸-剪切试验获得的载荷-位移曲线和失效形式。对于发生颈部断裂失效的接头，最大拉伸位移在0.6 ～1.2 mm;对于发生拉脱失效的接头，拉伸位移在1.2 ～2.0 mm。所有接头中，随着拉伸位移的增加，拉伸载荷增大。达到最大载荷后，图13(a)中载荷在一个较小的拉伸位移内迅速降低为零，这是由于上板颈部达到最大应力值发生突然断裂(见图14(a));图13(b)中最大载荷保持一段拉伸位移后开始下降，并降低到零，这是由于上板在从下板拉出的过程中，上板颈部不断发生塑性变形，直到上板从下板中脱出，上下板分离(见图14(b))。

3 结 论

(1)所建立的压印连接过程的有限元模型可以较好地模拟压印接头成形过程，接头截面形状与试验一致。并通过模拟结果研究变形过程中的金属流动规律，单元变形情况与金属组织流向具有一致的规律。

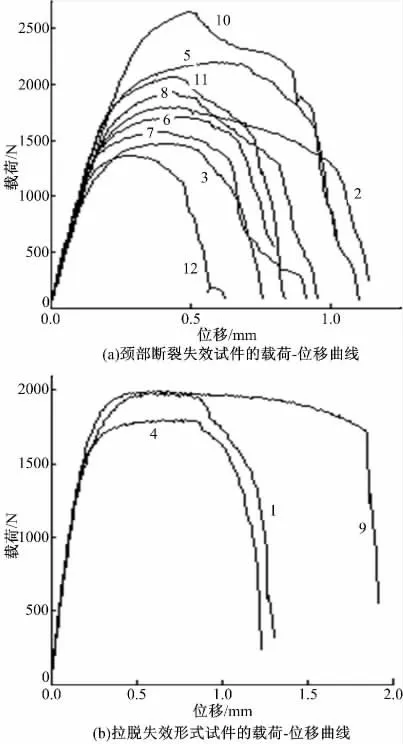
图13 12 种压印接头的载荷-位移曲线Fig.13 Load-displacement curves after tensile-shear tests for 12 clinched joints

图14 压印接头拉伸-剪切试验的失效形式Fig.14 Failure modes of clinched joints after tensile-shear tests

(2)由压印连接过程的模拟结果进行布尔运算得到接头拉剪的三维模型，模拟压印接头的拉剪过程。结果表明，充分考虑材料之间的接触和摩擦等非线性因素的有限元模型，可以较好地预测和分析压印接头强度及失效过程。

(3)根据压印接头颈部断裂失效和上下板拉脱失效分别提出了接头强度计算公式。提出的计算方法可以准确地预测压印接头拉剪强度和失效形式，计算误差不超过8.9%。

［1］李勇.TOX 板件冲压连接技术［J］.机械工程师，2003(5):58-60.Li Yong.TOX sheet metal stamping connection technology［J］.Mechanical Engineer，2003(5):58-60.

［2］Mori K，Abe Y，Kato T.Mechanism of superiority of fatigue strength for aluminium alloy sheets joined by mechanical clinching and self-pierce riveting［J］.Journal of Materials Processing Technology，2012，212(9):1900-1905.

［3］He X.Recent development in finite element analysis of clinched joints［J］.International Journal of Advanced Manufacturing Technology，2010，48(5-8):607-612.

［4］He X.Coefficient of variation and its application to strength prediction of clinched joints［J］.Advanced Science Letters，2011，4(4-5):1757-1760.

［5］De Paula A A，Aguilar M T P，Pertence A E M，et al.Finite element simulations of the clinch joining of metallic sheets［J］.Journal of Materials Processing Technology，2007，182(1-3):352-357.

［6］Varis J P.The suitability for round clinching tools for high-strength structural steel［J］.Thin-Walled Structures，2002，40(3):225-238.

［7］Varis J P.The suitability of clinching as a joining method for high-strength structural steel［J］.Journal of Materials Processing Technology，2003，132(1-3):242-249.

［8］周云郊，兰凤崇，黄信宏，等.钢铝板材压力连接模具几何参数多目标优化［J］.材料科学与工艺，2011，19(6):86-99.Zhou Yun-jiao，Lan Feng-chong，Huang Xin-hong，et al.Multi-objective optimization of geometry of clinching tools for steel-aluminum blank sheets［J］.Materials Science and Technology，2011，19(6):86-99.

［9］黄柳钧，何玉林.铝板无铆钉自冲铆接质量及强度的试验研究［J］.机械设计与制造，2010(11):98-100.Huang Liu-jun，He Yu-lin.An experimental research on quality and strength of aluminous joints by clinch joining technique［J］.Machinery Design＆Manufacture，2010(11):98-100.

［10］龙江启，兰凤崇，陈吉清.基于神经网络无铆钉自冲铆接接头力学性能预测［J］.计算机集成制造系统，2009，15(8):1614-1630.Long Jiang-qi，Lan Feng-chong，Chen Ji-qing.Neural network-based mechanical property predication in the mechanical clinching joints［J］.Computer Integrated Manufacturing Systems，2009，15(8):1614-1630.

［11］Lee C J，Kim J Y，Lee S K，et al.Design of mechanical clinching tools for joining of aluminium alloy sheets［J］.Materials and Design，2010，31(4):1854-1861.

［12］曹乃光.金属塑性加工原理［M］.北京:冶金工业出版社，1982.

［13］徐政坤.冲压模具及设备［M］.北京:机械工业出版社，2005.