电动汽车复合制动预测模型

郭洪强，何洪文，卢 兵

(北京理工大学 电动车辆国家工程实验室，北京100081)

0 引 言

制动能量回收是提高电动汽车驱动效率的重要手段，有效的复合制动系统可使电动汽车续驶里程增加10%～30%［1-2］。复合制动系统除要求具备较高的再生制动能量回收效率外，还应具备较佳的制动稳定性能［3］。电动汽车复合制动系统主要分为并联式及串联式。串联式需对现有制动系统进行改造，但可实现较好的复合制动特性;并联式无需对现有制动系统进行改造，但其再生制动能量回收效率的提高依赖于额外增加的总制动力需求，容易造成车轮提前抱死，降低制动效能［3］。

复杂系统的不同子系统之间往往存在强耦合关系，采用传统的优化方法难以得到收敛解。多学科优化设计可以充分利用子系统间相互作用产生的协调作用获得整体最优解，因而多学科优化方法是解决复杂系统优化问题的有效手段［4-6］。文献［7-9］基于ECE 制动法规，以制动稳定性为边界条件，对复合制动制动力分配的方法进行了研究，取得了较好的控制效果。但没有考虑最大化再生制动能量回收效率及最佳制动稳定性两个目标之间的平衡问题。文献［10-11］基于优化的方法对复合制动制动力分配的方法进行了研究，该方法能获得较好的复合制动特性，但是鉴于在线优化实时性差的缺陷，难以实现工程应用。

本文提出了制动强度二次再分数学模型，可确保并联式复合制动系统最大化回收再生制动能量且跟随总制动扭矩需求。提出了基于协同优化算法(CO)的复合制动制动力分配方法，可协调最大化再生制动能量回收效率及最佳制动稳定性两个目标。设计了离线优化流程，基于离线优化数据构建了关键参数的响应面模型，将响应面模型代入制动强度二次再分数学模型，构建了复合制动预测模型，解决了在线优化实时性差的问题。

1 复合制动系统构型

本文采用双电机动力耦合系统。制动时，基于复合制动控制器、液压制动器、电机1 和电机2协调对车辆前轴和后轴施加再生制动力。复合制动系统构型如图1 所示。

图1 复合制动系统构型Fig.1 Structure of the cooperative braking system

本文研究的是一般制动情况，即假定路面为良好的干燥路面，且路面能够提供足够的地面附着力，使车轮不会出现过大滑移。此外，在一般制动的情况下，制动减速度很少能超过3 m/s2［2］，因此，本文设定制动强度z 为0 ～0.4;考虑到最小电机转速及车速的限制，设定车速v 为20 ～100 km/h;考虑到电池的充电特性，设定电池SoC 为0.1～0.8。z、v 和SoC 构成了复合制动系统的连续设计空间。

2 制动强度二次再分数学模型

图2 为复合制动系统受力图。图2 中，Tm1、Tm2分别为电机1、2 作用到车轮处的再生制动扭矩;Thf、Thr分别为前、后液压制动器作用在车轮处的制动扭矩;rw为轮胎滚动半径;ωf、ωr分别为前、后轴车轮速度;Fxf、Fxr分别为前、后轴车轮地面制动力。

图2 复合制动系统受力图Fig.2 Force diagram of the cooperative braking system

复合制动时，总制动扭矩应为总电机再生制动扭矩Tm、Thf和Thr之和;Tm为Tm1和Tm2之和:

式中:Trm为总制动扭矩，其表达式为:

式中:mg 为整车质量。

制动强度二次再分方法要求:部分制动强度分配给双电机，其余制动强度分配给液压制动器，液压制动器按原比例阀特性进行制动力分配:

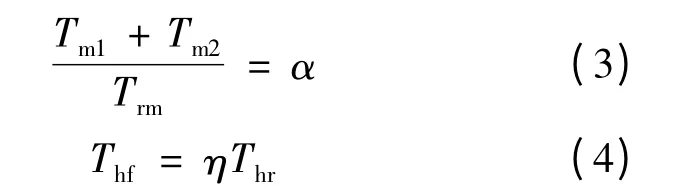
式中:α 为制动强度二次再分系数，优化算法中，其变化范围为0 ～1;η 为比例阀特性值，当制动强度小于0.4 时，其值为恒定值2.5。

为了满足制动稳定性要求，双电机再生制动扭矩需进行合理分配:

式中:γ 为双电机扭矩分配系数，优化算法中，其变化范围为0 ～1。

联立式(1)～(5)可求得:

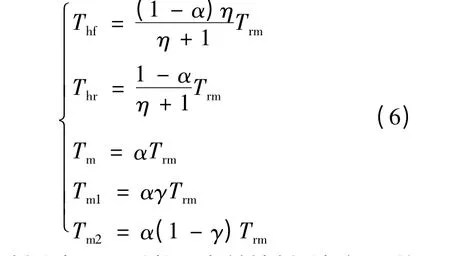
定义制动力分配系数β 为前轴制动扭矩与总制动扭矩之比:

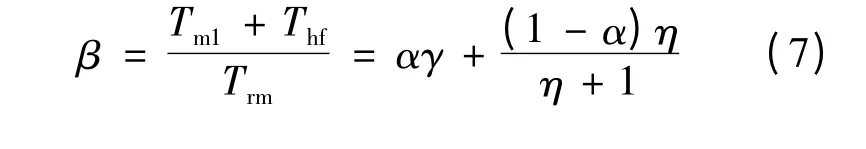
3 优化流程

基于ISIGHT 软件平台，采用分布式计算的方法实现。首先对连续设计空间进行DOE 采样，采样点为2000 组。然后将采样点传递给优化参数计算模块，计算协同优化算法所需的输入参数，优化后，将采样点及优化参数存入采样点优化数据库。最后，基于采样点优化数据库，构建关键参数的二阶响应面模型。

3.1 试验设计采样

较好的采样点分布是构建高精度响应面模型的基础［12］。最优拉丁超立方设计(Optimal latin hypercube design，Opt LHD)可对连续设计空间进行均匀采样，具有较好的空间填充性和均衡性，因而本文采用该方法进行采样，采样点如表1 所示。

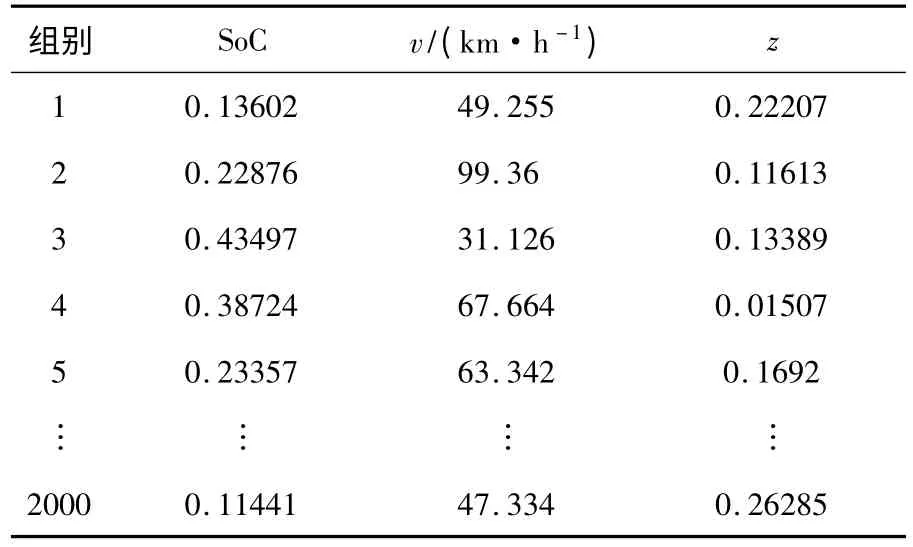
表1 连续设计空间采样点Table 1 Continuous design space's sampling points

3.2 优化参数计算模块

3.2.1 最大化制动能量回收目标值

理想充电扭矩主要取决于以下扭矩的最小值:①电池最大可充电扭矩:不同电池SoC 下，电池的最大可充电扭矩也不同;②不同转速电机的最大再生制动扭矩;③当车轮制动扭矩全部由电机承担时，地面附着力允许的最大制动扭矩。因此，复合制动系统在特定车速v、电池SoC 及制动强度z 下的理想充电扭矩为:

式中:Topt为理想充电扭矩;Tmot_brake为电机最大再生制动扭矩;Tbattery_charge为电池最大可充电扭矩;Tf为由地面附着力允许的最大制动扭矩。

3.2.2 最佳制动稳定性目标值

制动时，车辆如果按照理想制动力分配线(I曲线)进行分配，将会防止任何车轮提前抱死，此时，车辆可获得最佳的制动效能，同时也能获得较好的制动稳定性［9］，本文中将理想的制动力分配线(I 曲线)作为最佳制动稳定性的目标值:

式中:βopt为理想制动力分配系数;b 为后轴距;L为轴距;hg为质心高度。

3.2.3 约束边界条件

(1)总电机再生制动扭矩输出不能超过理想充电扭矩:

(2)Tm1和Tm2分别不能超过电机的峰值充电扭矩Tout1和Tout2:

式中:Tout1，Tout2为电机在给定转速下峰值充电扭矩，其值由电机转速及充电扭矩特性曲线通过插值方法得到。

(3)前后轮总制动扭矩均不能超过地面附着力允许的前后轮最大制动扭矩Tf1和Tf2:

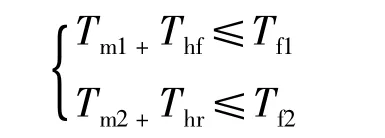
(4)根据国家制动法规ZBT24007－1989(在各种装载情况下，总质量大于3.5 t 的货车)及稳定性的要求，制动力分配系数与制动强度的关系可用式(10)表达:

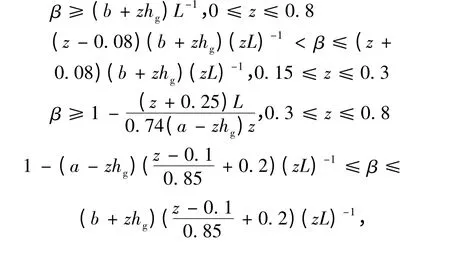
式中:a 为前轴距。

式(10)可作为优化算法中制动稳定性的约束条件，以制动强度z 为横坐标，制动力分配系数β 为纵坐标，可画出稳定制动区域(见图3)，图中，a，b，c，d，e 为由式(10)决定的边界线;I 为理想制动力分配线。

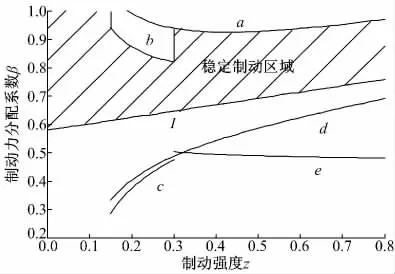
图3 稳定制动区域Fig.3 Braking stability scope

3.3 协同优化算法

复合制动系统优化主要存在以下难点:

(1)再生制动能量回收和制动稳定性之间存在强耦合系统变量，约束主要为系统变量的表达式形式，且较为复杂。

(2)本文研究在2000 组采样点下的优化问题，每组采样点输入均需做优化，因此，优化算法的自适应性及收敛性是本优化问题的一个难点。

(3)收敛解的精度及总优化时间(小于24 h)需得到保证。

该优化问题也可作为一多目标优化问题，处理方式一般有两种:①通过引入权值系数将多目标优化问题转化为单目标优化问题进行求解。对于本优化问题，如果采用梯度算法，难以跳出局部最优;如果采用自适应模拟退火算法(ASA)，其收敛性、算法自适应性及优化时间能得到保证，但难以收敛到较好的解;如果采用多岛遗传算法，则容易发散且优化时间过长。②采用多目标优化算法求解。对于矛盾目标的优化问题，一般采用该算法。对于本优化问题，因其为一致性目标优化问题，所以无需采用该算法。

本文中，协同优化算法系统层及子系统层均采用自适应模拟退火算法(ASA)，可以保证较好的收敛性及自适应性;基于分布式计算的方法可保证优化时间［13-14］。基于系统层与子系统层的不断协调，可得到较好的收敛解。

图4 为协同优化算法示意图。如图5 所示，协同优化算法的系统层目标为复合制动系统总目标，采用归一化处理保证两目标值数量级一致，设定两目标具有同等重要的地位(权值系数为1)。系统层约束为子系统层目标，其为保证子系统一致性的约束条件，此外，为保证算法的收敛性，定义松弛因子ε 为1×10－4。系统变量为α 和γ，在系统层分别以z1和z2描述。一般来说，协同优化算法需区分系统层与子系统层设计变量，对于本优化问题，因仅涉及两个设计变量α 和γ，所以构建协同优化算法时，子系统层设计变量也为α 和γ。优化流程:

图4 协同优化算法Fig.4 Collaborative optimization algorithm

(1)系统层向各子系统层下发系统变量值，该值作为各子系统层的固定值，各子系统层不断寻优并找到满足本子系统目标及约束的设计变量值及目标值。

(2)将各子系统层目标值反馈给系统层，系统层判断该值是否满足子系统一致性约束条件，同时判断当前系统目标值是否满足收敛条件，如果满足则停止;反之则重复步骤(1)，重新下发系统设计变量。

3.4 构建预测模型

响应面法是一种用来获取一组独立变量与系统响应之间某种近似关系的统计技术，该方法可得到确定的数学表达式，有利于后期控制算法的开发。此外，鉴于本文设计空间较弱的非线性特点，采用二阶响应面模型。响应面模型中，常采用复相关系数R 度量对原函数的逼近程度，R 值的范围为(0，1)，越接近1，说明拟合精度越高，本文采用R2来进行评价［15］。

以采样点(见表1)作为输入，自变量α、γ 和β的优化解αopt、γopt及βopt作为输出，基于二阶响应面的方法，可构建对应αopt、γopt及βopt的响应面模型和。该响应面模型可作为在某一样本点输入下αopt、γopt及βopt的预测模型。本文取拟合精度较高的α^及β^作为预测模型:

将式(11)(12)代入式(6)(7)，可得到复合制动预测模型如下:

4 仿真验证

基于Matlab/Simulink 仿真环境，搭建整车复合制动仿真模型。设定路面附着系数为0.8，初始车速为86 km/h，初始SoC 为0.5。三次简单制动过程如图5 ～图7(a)所示，其中t0为制动过程中的反应时间、协调时间及二分之一制动力上升时间的总和;t1、t2和t3为三次简单制动时间。

为了验证预测模型的实时性，本文对比进行了在线优化仿真(Matlab 调用ISIGHT 进行联合优化)及基于预测模型的仿真两种计算。此外，为进一步校核预测模型精度，定义相对误差评价参数如下:

图5 在线优化与预测模型仿真结果对比Fig.5 Simulation comparison results between the online optimization and the predictive model

图6 复合制动仿真结果1Fig.6 Cooperative braking simmulation result 1

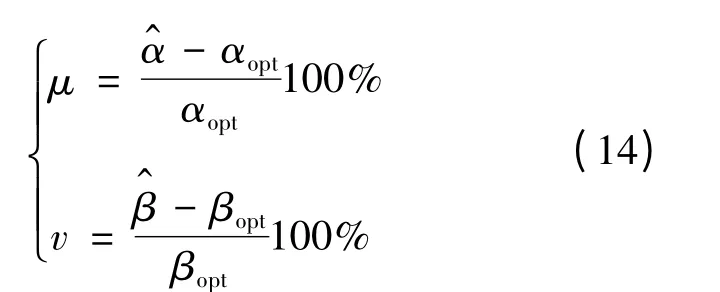
式中:μ 为αopt的评价参数;v 为βopt的评价参数。

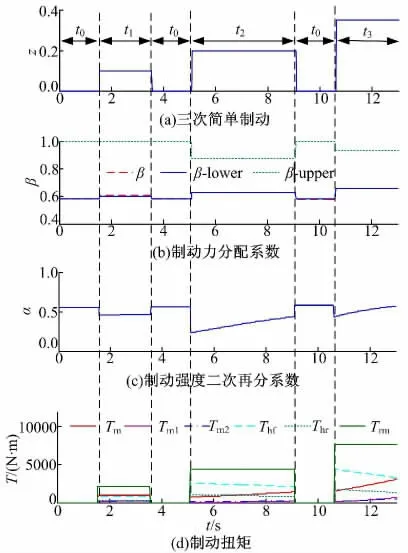
图7 复合制动仿真结果2Fig.7 Cooperative braking simulation result 2

如图5(b)所示，预测模型预测值与在线优化解相对误差均较小，最大相对误差为5.6%，说明预测模型具有较高的预测精度。此外，在线优化仿真时间为11.3 h，而基于预测模型的仿真时间为1.16 s，说明预测模型具有较好的实时性。

如图6 和图7 所示，在t0制动过程，SoC、v 均保持不变，无制动扭矩输出。α，γ 虽有输出值，但受限于Trm(见式2)，对图7(d)的制动扭矩输出无任何影响。t1、t2和t3制动过程中，SoC 线性增加，并正比于图7(d)中Tm值的变化;v 线性降低并反比于图7(d)中Trm的变化。为了满足优化目标的要求，α 进行制动强度二次再分，γ 协调双电机扭矩分配系数。β 始终处于稳定制动区域，而且接近于β-lower，β-lower 为制动稳定性下限，同时也是理想制动力分配线(见图4)，这说明制动过程中，车辆能保持较好的制动稳定性能。

5 结束语

系统分析了并联式复合制动系统制动力分配预测模型的设计方法。提出的制动强度二次再分数学模型，通过合理分配制动强度，可在不额外增加总制动扭矩的前提下，改善复合制动特性。提出的复合制动协同优化算法，可协调最大化再生制动能量回收效率及最佳制动稳定性两个目标。此外，仿真结果表明:提出的基于DOE 采样-离线优化-构建预测模型-在线预测控制的解决方案可解决在线优化实时性差的问题。

［1］王昕，姜继海.轮边驱动液压混合动力车辆再生制动控制策略［J］.吉林大学学报:工学版，2009，39(6):1544-1549.Wang Xin，Jiang Ji-hai.Regenerative braking control strategy for wheel drive hydraulic hybrid vehicle［J］.Journal of Jilin University(Engineering and Technology Edition)，2009，39(6):1544-1549.

［2］仇斌，陈全世，张开斌.北京市区电动轻型客车制动能量回收潜力［J］.机械工程学报，2005，41(12):87-91.Qiu Bin，Chen Quan-shi，Zhang Kai-bin.Braking energy recycle of light electric bus of Beijing town［J］.Chinese Journal of Mechanical Engineering，2005，41(12):87-91.

［3］张俊智，薛俊亮，陆欣，等.混合动力城市客车串联式制动能量回馈技术［J］.机械工程学报，2009，45(6):102-106.Zhang Jun-zhi，Xue Jun-liang，Lu Xin，et al.Series braking energy recycle technology of hybrid electric city bus［J］.Chinese Journal of Mechanical Engineering，2009，45(6):102-106.

［4］马明旭，王成恩，张嘉易，等.复杂产品多学科设计优化技术［J］.机械工程学报，2008，44(6):15-26.Ma Ming-xu，Wang Cheng-en，Zhang Jia-yi，et al.Multidisciplinary optimization technology of the complicate production［J］.Chinese Journal of Mechanical Engineering，2008，44(6):15-26.

［5］Yang R J，Gu L，Tho C H.Multidisciplinary design optimization of a full vehicle with high performance computing［C］∥AIAA Paper，2001-1273.

［6］Kodiyalam S，Yang R J，Gu L，et al.Multidisciplinary design optimization of a vehicle system in a scalable，high performance computing environment［J］.Struct Multidisc Optim，2004，26(3-4):256-263.

［7］李玉芳，周丽丽.纯电动汽车电-液复合制动系统控制算法的多边界条件优化设计［J］.中国机械工程，2012，23(21):2634-2640.Li Yu-fang，Zhou Li-li.Optimization design of ev electro-hydraulic composite braking system control algorithm with mul-boundary conditions［J］.Chinese Journal of Mechanical Engineering，2012，23(21):2634-2640.

［8］郑宏宇，许文凯，刘宗宇，等.四轮独立驱动电动汽车再生制动控制策略［J］.吉林大学学报:工学版，2013，43(3):590-594.Zheng Hong-yu，Xu Wen-kai，Liu Zong-yu，et al.Control strategy regenerative braking for four-wheeldrive electric vehicle［J］.Journal of Jilin University(Engineering and Technology Edition)，2013，43(3):590-594.

［9］宗长富，张继红，陈国迎，等.四轮驱动与前轮驱动电动车的再生制动性能［J］.吉林大学学报:工学版，2010，40(增刊1):24-28.Zong Chang-fu，Zhang Ji-hong，Chen Guo-ying，et al.Investigating regenerative braking performance of 4WD and FWD electric vehicle［J］.Journal of Jilin University(Engineering and Technology Edition)，2010，40(Sup.1):24-28.

［10］Hellgren J，Jonasson E.Maximisation of brake energy regeneration in a hybrid electric parallel car［J］.International Journal of Electric and Hybrid Vehicles，2007，1(1):95-121.

［11］郭金刚，王军平，曹秉刚.基于优化的电动车制动力分配［J］.机械科学与技术，2011，30(9):1495-1499.Guo Jin-gang，Wang Jun-ping，Cao Bin-gang.Optimization based braking force distribution for electric vehicles［J］.Mechanical Science and Technology for Aerospace Engineering，2011，30(9):1495-1499.

［12］Park J S.Optimal Latin-hypercube designs for computer experiments［J］.Journal of Statistical Planning and Inference，1994，39(1):95-111.

［13］Tappeta R V，Renaud J E.Multiobjective collaborative optimization［J］.Journal of Mechanical Design，1997，119(3):403.

［14］Zhou W，Wang D，Sheng J，et al.Collaborative optimization of maintenance and spare ordering of continuously degrading systems［J］.Journal of Systems Engineering and Electronics，2012，23(1):63-70.

［15］Myers R H，Anderson-Cook C M.Response Surface Methodology:Process and Product Optimization Using Designed Experiments［M］.USA:Wiley Press，2009.