基于扰动观测器的电动助力转向系统用永磁同步电机鲁棒预测电流控制

张 虎，张建伟，郭孔辉，李 洋

(吉林大学 汽车仿真与控制国家重点实验室，长春130022)

0 引 言

电动助力转向系统(Electric power steering，EPS)以其高效、节能和安装方便等优点正逐渐取代液压助力转向系统成为汽车动力转向系统的发展趋势。EPS 的助力电机主要有直流有刷电机、直流无刷电机、永磁同步电机和感应电机。相比于其他几种助力电机，永磁同步电机以其高能量密度、高转矩惯量比、高可靠性和转矩脉动小等优点越来越多地应用到EPS 中［1］。

目前常用的EPS 用永磁同步电机电流控制策略为基于矢量控制的同步坐标系下的PI 控制。但是矢量控制仅实现了dq 轴电流的静态解耦，动态过程中交叉耦合项的存在会影响电流跟踪性能。为此，文献［2-3］提出了前馈解耦、反馈解耦、内模解耦和逆系统解耦等各种解耦方法来提高电流动态性能。此外，传统PI 电流控制调节时间长且容易超调，很难兼顾EPS 系统对电流响应的快速性和稳定性的要求。

除传统的PI 电流控制外，滞环控制、无差拍控制等方法也被广泛应用于永磁同步电机电流环的控制。滞环控制响应迅速且对电机参数不敏感［4］，但其控制的电流波纹大且开关频率不定，不适用于EPS 系统。无差拍电流控制能够在有限拍时间内无差跟踪目标电流值，响应快速且无超调，但其控制性能依赖于精确的电机模型，另外，与其他控制方法一样，其稳定性受控制延迟的影响，因此在实际应用中应对无差拍控制进行改进。针对控制延时问题，文献［5-6］提出将延时放到电机模型中并对电机电流进行向前一步预测的方法消除系统延时对稳定性的影响。针对电机电感参数摄动问题，文献［7-8］提出采用状态观测器预测下一时刻电机电流，并通过调整状态观测器的增益扩展了系统稳定性对模型电感误差的容许范围。但上述方法并未考虑其他电机参数摄动及扰动对系统鲁棒性能的影响。文献［9］采用参数在线辨识的方法来消除电机参数波动对系统性能的影响，但辨识过程繁琐且辨识结果受采样噪声的影响。

针对上述问题，本文首先利用反馈解耦消除了电压交叉耦合项对系统动态性能的影响。在此基础上建立了考虑系统延时和扰动的电机解耦模型。分析了系统延时、电机参数摄动和其他系统扰动对无差拍电流控制器动态性能和稳态性能的影响，提出了一种由无差拍控制器、电流状态观测器和自适应扰动观测器构成的鲁棒预测无差拍电流控制(ARPCC)算法，电流状态观测器用于保证无差拍控制系统的稳定性，自适应扰动观测器用于提高系统的跟踪精度。然后对所提控制器的无差拍性能和稳定性进行了分析，并在一台460 W的EPS 永磁同步电机上对所提控制算法的有效性进行了试验验证。

1 永磁同步电机的数学模型

1.1 永磁同步电机基本模型

忽略磁路饱和、磁滞和涡流的影响，假设定子三相绕组对称且绕组电流在气隙中产生的磁动势为正弦分布，则在同步dq 轴坐标系下，表贴式永磁同步电机电流动态方程可以表示为:

式中:id、iq、ud和uq分别为电机dq 轴的电流和电压;R、L 和ψ 分别为电机定子电阻、定子电感和转子磁链;ωe为电角速度。

由式(1)可知，矢量控制仅实现了dq 轴电流的静态解耦，在动态过程中，由于交叉耦合项ωeiq和ωeid的存在造成两轴电流相互影响，使dq 轴电流控制精度降低，动态过程变慢［2］。因此要实现电机良好的动、静态性能，必须先对交叉耦合项进行补偿，本文采用反馈解耦的方法来消除交叉耦合项对系统性能的影响。令:

式中:i =［id，iq］T;v =［vd，vq］T;ac=－R/L，bc=1/L。

由式(3)可知，dq 轴电流状态方程被解耦为两个完全相同的单输入、单输出一阶惯性环节。上述状态方程式(3)的解为:

考虑到逆变器零阶保持特性，令t0=kT，且t=(k+1)T，则式(4)可以离散化为:

1.2 考虑延时及扰动的永磁同步电机模型

图1 为数字电流控制器的时序图，理想的控制器采样、计算和控制量的输出都是在采样时刻kT 完成的。但实际上，从电流控制开始到控制结束存在两个采样周期的延时。第一个延时用于电流等信号的采集及控制算法的计算，逆变器的零阶保持特性引入了第二个延时［5］。

图1 数字电流控制器时序图Fig.1 Timing sequence of the digital current controller

此外，系统运行过程中，电机参数摄动、电机转子位置信号和电流信号的扰动、蓄电池电压波动、逆变器非线性和电机的未建模动态都会影响电流控制器的鲁棒性能，因此本文将其统一作为系统扰动处理，其表达式为:

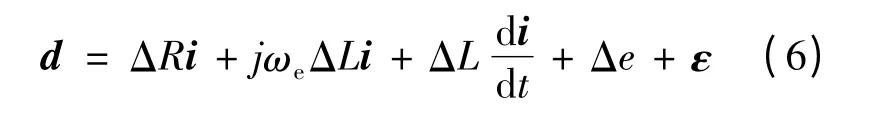
在状态方程(3)的解中引入延时td=T 和式(6)所述的不确定性扰动，并令id(t)=i(t－td)则有:

将t0=kT－td和t=(k+1)T 代入式(7)得:

假设在采样周期内扰动d(t)不变且施加在

电机上的电压保持恒定，并令dd(t)=d(t－td)则有:

由式(8)(9)可得考虑延时及扰动的永磁同步电机离散模型为:

2 无差拍电流控制的动态分析

无差拍电流控制能够在有限拍的时间内实现电机电流对给定电流的无差跟踪［10］。当延迟时间满足td≪T 时，即忽略采样和计算延时，电机电流动态方程可由式(5)表示，令i(k +1)=iref(k)，则无差拍控制率可以表示为:

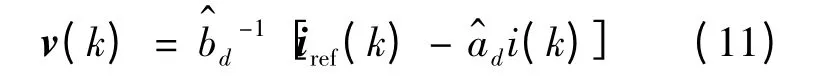
由式(5)(11)得无差拍电流控制框图，如图2 所示。

图2 无差拍电流控制框图Fig.2 Block diagram of the deadbeat current control

当忽略采样和计算延时时，无差拍电流控制能够在一个采样周期内实现电机电流对给定电流的无差跟踪。但实际上当延迟时间与控制周期相当时，由数字控制本身不可避免的延时也会降低系统的稳定裕度。图3 为考虑延时的无差拍电流控制框图。

由控制框图3 可知，考虑延时的无差拍电流控制闭环传递函数为:

由式(13)可知，当β=1 时，闭环传递函数简化为T(z)=1/(z2－z+1)，系统的两个闭环极点都位于单位圆上，系统稳定裕度大大降低。系统稳定的条件为:0 ＜β ＜1。因此延时的存在使系统的无差拍控制性能劣化。

由上述分析可知，无差拍电流控制器的稳定性受到系统延时和电感参数摄动的影响。另外，电机参数摄动、各采样信号的扰动、逆变器非线性和电机模型中的未建模动态等扰动也会影响电流控制的鲁棒性能。

图3 考虑延时的无差拍电流控制框图Fig.3 Block diagram of the deadbeat current control with time delay

3 基于扰动观测器的鲁棒预测电流控制算法设计及分析

为了补偿采样和计算延时以及系统扰动，提高系统的稳定性和控制精度，本文在无差拍电流控制基础上增加电流观测器和扰动观测器。电流观测器预测电机电流补偿系统延时并通过调整观测器增益扩展系统稳定性对电感摄动容许范围，从而提高系统的稳定裕度。扰动观测器可以估计包括电机参数变化、车载蓄电池电压波动、逆变器非线性以及其他一切扰动的综合作用［11］，从而提高系统的鲁棒性能。

3.1 鲁棒预测电流控制算法设计

假设系统扰动dd(k)已知，为了补偿采样和计算延迟，提高系统稳定性，将式(10)超前一个采样周期，并且令id(k+2)=iref(k)得电流控制系统的无差拍控制率:

之所以称之为预测控制是因为需要预测下一时刻的电机电流id(k+1)和扰动dd(k+1)。

k+1 时刻的扰动dd(k+1)可以利用拉格朗日差值公式预测得到:

本文采用状态观测器预测k+1 时刻的电机电流id(k+1)。电流观测器的差分方程为:

系统带宽和收敛速度取决于观测器极点的位置。此状态观测器的极点为，为了保证系统的稳定性，状态观测器增益值应满足0 ＜Lso＜2。

3.2 自适应扰动观测器设计

本文采用基于李雅普诺夫稳定理论的自适应观测器估计系统扰动dd(k)，由状态方程式(10)构造自适应观测器的参考模型如下:

则其可变模型可以表示为:

构造如下李雅普诺夫函数:

式中:λ 为大于零的实数。

由李雅普诺夫稳定理论［12］可知，要使系统全局渐进稳定必须满足:

对式(20)李雅普诺夫函数求导得:

由式(22)得系统扰动自适应率为:

自适应率的离散化形式为:

3.3 鲁棒预测电流控制的无差拍性能及扰动观测器稳定性分析

由式(14)(16)得鲁棒预测电流控制框图如图4 所示。

图4 鲁棒预测电流控制框图Fig.4 Block diagram of the robust predictive current control

由控制框图4 知，鲁棒预测电流控制开环传递函数为:

假设β ≈1，则系统的闭环传递函数为:

由式(26)可知，对于任意的状态观测器增益Lso，鲁棒预测控制都是两个采样延时的无差拍控制，即电机电流经过两个控制周期后实现对给定电流的无差跟踪。其闭环特征方程为(z+Lso)(z－1)+Lsoβ =0，由July 判据可知，当β ∈［0，(1+Lso)/Lso］时系统稳定。减小观测器增益Lso能够在不改变无差拍性能的前提下扩展对电感不确定的容许范围，增加了系统的稳定裕度。

为了确定式(24)中的自适应增益λ 的取值范围，引入离散域李雅普诺夫函数:

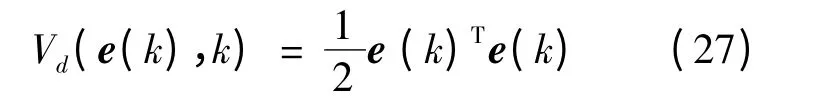
则自适应律能够使观测器稳定的条件为:

由式(27)为正定二次型函数知，要使式(28)成立只需满足:

将式(19)(24)(27)的离散式代入式(29)得:

此外，由于实际的系统扰动都是在一定范围内变化的，为了保证自适应观测器的有界稳定性，将估计的扰动(k)限制在内。

4 仿真及试验结果分析

对提出的基于自适应扰动观测器的鲁棒预测电流控制(ARPCC)算法的性能进行仿真和试验验证。仿真和试验验证用转向助力电机参数如下:额定功率为460 W;额定转速为1050 r/min;额定转矩为4.2 N·m;额定电流为113 A;定子电阻为0.0143 Ω;定子电感为66.2 μH;转子磁链为0.00618 Wb;极对数为4。由于算法是基于矢量控制的，故采用SVPWM 调制方法，电流的采样和控制周期均为50 μs。

4.1 仿真结果及分析

仿真环境为Matlab/Simulink，本文所提出的ARPCC 算法中状态观测器增益Lso=0.5，扰动观测器增益λ=0.4。

图5 给出了文献［7］提出的鲁棒预测电流控制(RPCC)算法和本文提出的ARPCC 算法忽略逆变器非线性而电阻增大80%时的q 轴电流控制效果。其测试工况为:q 轴目标电流设为频率为1 Hz、幅值为113 A 的正弦电流信号，负载为4 N·m 以模拟EPS 原地转向工况(工况1)。图中和Δiq_ARPCC分别表示q 轴目标电流、RPCC 算法控制误差和ARPCC 算法控制误差，由图5 可知，RPCC 控制器电流稳态误差随电流的增大而增加，最大达到3 A 左右，而本文提出的ARPCC 控制器无论电流大小都没有稳态误差。

图5 电阻增加80%两种控制算法的仿真结果Fig.5 Simulation results of two control algorithms

图6 给出了两种控制算法忽略逆变器非线性而磁链降低50%时的q 轴电流控制效果。其测试工况为:电机转速在0.02 s 时从静止阶跃到1000 r/min，电机目标电流从0 A 阶跃到30 A 以模拟较高车速下EPS 快速转向工况(工况2)。从图6 可以看出，RPCC 算法电流稳态误差随电机转速升高而增大，最大达到2 A 左右，而本文提出的ARPCC 算法静态误差几乎为零。

图6 磁链减少50%两种控制算法的仿真结果Fig.6 Simulation results of two control algorithms

图7 为电机参数准确、逆变器死区时间为2 μs 时，在工况1 下两种控制算法的电流跟踪效果。由图7 可知，本文提出的ARPCC 算法能有效地抑制由逆变器非线性引入的扰动，而RPCC 算法不能抑制此扰动。

图7 考虑死区时间两种控制算法的仿真结果Fig.7 Simulation results of two control algorithms with deadtime

图8 为两种控制算法在蓄电池电压波动时在工况1 下的电流跟踪效果，由于在工况1 下由EPS 引起的蓄电池电压波动较明显，且随电流的增大而减小。因此，假设蓄电池电压的波动波形如图8 中VBus所示。从图8 可以看出:RPCC 算法的稳态误差随着蓄电池电压的降低而增大，而本文提出的ARPCC 算法没有稳态误差。

图8 蓄电池电压波动时两种控制算法的仿真结果Fig.8 Simulation results of two control algorithms with a fluctuation in the power supply

4.2 试验结果及分析

试验环境如图9 所示，试验平台由以TI 公司的TMS320F28335 DSP 作为主控芯片的电流控制器、EPS 用永磁同步电机和一台加载电机组成。

图9 试验平台Fig.9 Experimental platform

图10 为传统的PI 控制算法与本文提出的ARPCC 算法的控制效果。理想情况下，本文提出的ARPCC 算法可以在两个采样周期内跟踪目标值，然而受蓄电池电压(12 V)限制实现无差跟踪的时间有所延长，但从图中可以看出:调整PI 参数使传统PI 控制算法与ARPCC 算法有相当的响应速度时，PI 控制算法与ARPCC 算法相比有较大超调。

图10 传统PI 控制与ARPCC 控制的瞬态过程Fig.10 Dynamic process of the PI control and ARPCC

图11 考虑死区时间两种控制器的试验结果Fig.11 Experimental results of two control algorithms with deadtime

图11 给出了电机参数准确但不对逆变器死区进行补偿时，RPCC 算法与ARPCC 算法在目标电流为50 A 恒定值下的控制效果，如图11 所示，由于RPCC 算法没有考虑逆变器非线性的扰动，电流跟踪的稳态误差大约在2 A 左右，而本文提出的ARPCC 算法很好地抑制了上述扰动，电流跟踪不存在稳态误差。

本文在电机三相绕组中各串联阻值为10 mΩ的导线以模拟助力电机长时间大电流运行工况下，因绕组温度升高引起的电机电阻的增加。图12 给出了补偿逆变器非线性但电机电阻增加70%时(即每相串联一条10 mΩ 导线)，两种控制算法在工况1(目标电流幅值100 A)下的试验结果，由图12 可以看出:由于RPCC 算法在计算控制率时电机参数使用的是标称值，因此在电机电阻增大时，RPCC 控制算法不可避免地出现了稳态误差，且稳态误差随着电机电流的增大而增大。相反，本文提出的ARPCC 算法对电机参数变化引起的扰动进行了相应的估计和补偿，因此即使在电机电阻变化时也不会产生静态误差。

图12 电阻增加70%两种控制算法的试验结果Fig.12 Experimental results of two control algorithms

图13 模型磁链增加50%时两种控制算法的试验结果Fig.13 Experimental results of two control algorithms

因降低电机永磁体磁链值比较困难且有可能导致其退磁，故本文将电机模型中的磁链增大50%以模拟实际电机磁链减小。图13 给出了补偿逆变器非线性但ψ^ =1.5ψ 时两种控制算法在工况2 下的试验结果。如图13 所示，当电机转子磁链减小时，RPCC 算法电流跟踪出现稳态误差，当转速达到1000 r/min 时，稳态误差大约2 A 左右，而本文提出的ARPCC 算法电流跟踪误差在较短时间内即收敛到0。

5 结束语

无差拍电流控制算法的稳定性受控制延时和电机电感参数变化的影响;而电机参数的变化和系统其他扰动影响无差拍控制的鲁棒性能。本文提出的ARPCC 算法在保证无差拍电流控制快速响应性能的前提下，通过引入状态观测器并改变观测器增益提高了系统的稳定性，通过引入自适应扰动观测器并对扰动进行补偿消除了电流环的静态误差。仿真和试验结果表明:本文提出的ARPCC 算法比传统的PI 电流控制响应速度更快，比RPCC 算法有更高的电流跟踪精度，因此更适于EPS 电流环的控制。

［1］Mohamed Y A R I.Design and implementation of a robust current-control scheme for a PMSM vector drive with a simple adaptive disturbance observer［J］.IEEE Transactions on Industrial Electronics，2007，54(4):1981-1988.

［2］杨明，付博，李钊，等.永磁同步电动机矢量控制电压解耦控制研究［J］.电气传动，2010，40(5):24-28.Yang Ming，Fu Bo，Li Zhao，et al.Research on voltage decoupling control of vector control for permanent magnet synchronous motor［J］.Electric Drive，2010，40(5):24-28.

［3］刘贤兴，胡育文.永磁同步电机的神经网络逆动态解耦控制［J］.中国电机工程学报，2007，27(27):72-76.Liu Xian-xing，Hu Yu-wen.Dynamic decoupling control of PMSM based on neural network inverse method［J］.Proceedings of the CSEE，2007，27(27):72-76.

［4］Cortés P，Kazmierkowski M P，Kennel R M，et al.Predictive control in power electronics and drives［J］.IEEE Transactions on Industrial Electronics，2008，55(12):4312-4324.

［5］Moon H T，Kim H S，Youn M J.A discrete-time predictive current control for PMSM［J］.IEEE Transactions on Power Electronics，2003，18(1):464-472.

［6］Lee Kui-Jun，Park Byoung-Gun，Kim Rae-Young，et al.Robust predictive current controller based on a disturbance estimator in a three-phase grid-connected inverter［J］.IEEE Transactions on Power Electronics，2012，27(1):276-283.

［7］Huerta J M E，Castelló-Moreno J，Fischer J R，et al.A synchronous reference frame robust predictive current control for three-phase grid-connected inverters［J］.IEEE Transactions on Industrial Electronics，2010，57(3):954-962.

［8］牛里，杨明，王庚，等.基于无差拍控制的永磁同步电机鲁棒电流控制算法研究［J］.中国电机工程学报，2013，33(15):78-85.Niu Li，Yang Ming，Wang Geng，et al.Research on the robust current control algorithm of permanent magnet synchronous motor based on deadbeat control principle［J］.Proceedings of the CSEE，2013，33(15):78-85.

［9］Jeong Se-Jong，Song Seung-Ho.Improvement of predictive current control performance using online parameter estimation in phase controlled rectifier［J］.IEEE Transactions on Power Electronics，2007，22(5):1820-1825.

［10］杨勇，阮毅，吴国祥，等.基于DPWM1 的无差拍解耦控制的三相并网逆变器［J］.电工技术学报，2010，25(10):101-107.Yang Yong，Ruan Yi，Wu Guo-xiang，et al.Deadbeat decoupling control of three-phase grid-connected inverters based on DPWM1［J］.Transactions of China Electrotechnical Society，2010，25(10):101-107.

［11］郭卫农，陈坚.基于状态观测器的逆变器数字双环控制技术研究［J］.中国电机工程学报，2002，22(9):64-68.Guo Wei-nong，Chen Jian.Study on digital dual-loop control for inverters based on state observer［J］.Proceedings of the CSEE，2002，22(9):64-68.

［12］胡寿松.自动控制原理［M］.5 版.北京:科学出版社，2007:516-517.