应用主成分分析的原棉可纺性指数构建
2015-06-09刘建立高卫东
苟 捷, 刘建立, 高卫东
(生态纺织教育部重点实验室(江南大学), 江苏 无锡 214122)
应用主成分分析的原棉可纺性指数构建
苟 捷, 刘建立, 高卫东
(生态纺织教育部重点实验室(江南大学), 江苏 无锡 214122)
为实现大容量纤维检测(HVI)指标在原棉品质评价中的合理应用,并为配棉提供参考,提出了一种基于主成分分析的原棉品质综合评价方法。首先选取不同产地、不同等级的284种原棉进行HVI检测,为消除指标间存在的冗余信息,选择了13项指标进行主成分分析;然后,利用提取的6项主成分因子构建原棉可纺性指数(FSI),实现了原棉品质的定量化评价;最后,讨论了FSI与成纱强力之间的相关性。研究结果表明,FSI指数越高,成纱强力越高,对应原棉的可纺性能越好。基于主成分分析的原棉评价方法能够定量评价棉纤维的可纺性能,可为原棉品质管理及成纱质量预测提供参考。
原棉; 品质评价; 可纺性; 主成分分析; 纱线强力
配棉是纺纱工艺的最前期工作,其核心在于充分掌握原棉的各项品质参数,根据纺纱实际要求,合理搭配原棉,充分发挥不同原棉的特点,优劣互补,达到提高产品质量、稳定生产、降低成本的目的[1]。随着国家棉花质量新标准的贯彻实施,原棉感官检验已逐步被仪器检验取代,大容量纤维检测仪(HVI)可快速提供原棉的各项性能指标,为后续生产提供技术参考,因此,研究众多HVI指标对原棉综合品质的贡献程度和对纱线质量的影响,对实现纺织企业信息化改造具有重要的技术经济意义。
与传统棉花检验方法相比,HVI仪器化检验可准确快速地提供原棉的17项性能指标:回潮率、马克隆值、成熟度指数、断裂比强度、断裂伸长率、上半均长、长度整齐度、短纤率、反射率、黄度、色特征级、荧光度、杂质数量、杂质面积、杂质等级、棉结数以及纺稳参数SCI。经验证,HVI指标间存在较强的相关性,例如:成熟度指数是由马克隆值、断裂比强度和断裂伸长率经过推算得出的[2]。如果直接利用众多HVI指标进行原棉综合评价,必然导致信息重叠,影响评价结果的合理性,因此,本文对HVI指标进行主成分分析,尽可能消除指标间的相关性,达到剔除冗余信息的目的,然后通过构建可纺性指数,实现原棉品质的客观评价。
1 评价指标及其检测结果
本文研究以某纺织企业2012—2013年度购入的284种不同产地(美国、巴西、新疆、山东、河南等)、不同等级(1~4级)的原棉棉样为研究对象,将所有样品放置于温度为(20±2) ℃,相对湿度为(65±2)%的环境中24 h,然后进行HVI检测。
在进行主成分分析前,剔除了受温湿度影响较大的回潮率以及杂质等级、色特征级等已经量化的等级指标,利用其余13项指标进行评价。为方便起见,标记各项指标:马克隆值为X1,成熟度指数为X2,断裂比强度为X3,断裂伸长率为X4,上半均长为X5,长度整齐度为X6,短纤率为X7,反射率为X8,黄度为X9,杂质数量为X10,杂质面积为X11,棉结数为X12,纺稳参数为X13,检测结果如表1所示(限于篇幅,本文仅列出部分数据)。
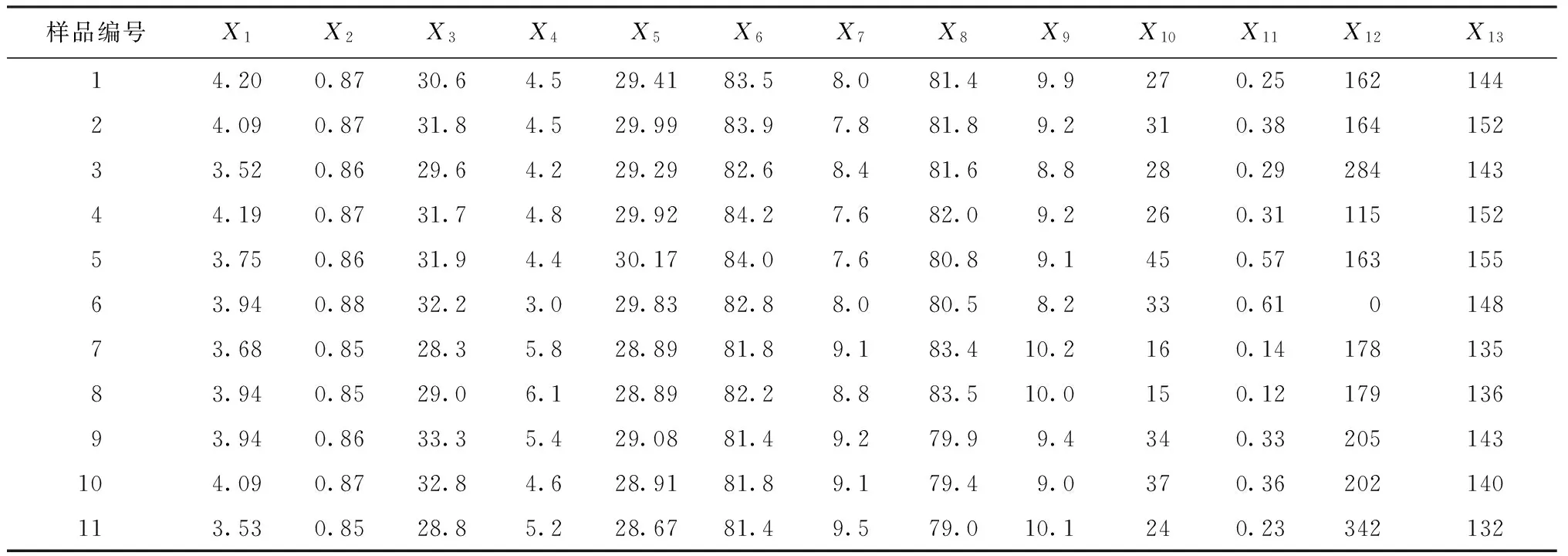
表1 原棉各项品质参数Tab.1 Quality parameters of raw cotton
2 HVI指标的主成分分析
主成分分析是一种基于统计学原理的描述系统低维模型的方法,其原理是通过对原始数据(本文为284种原棉的13项HVI指标)相关矩阵内部结构关系的研究,尽可能减少原始数据间的冗余信息,提取综合指标(主成分因子),在保留绝大部分重要信息的基础上较简洁地对样本进行综合评价。
主成分分析的一般步骤[3]为:1) 确定研究变量,整理数据,对样本数据进行标准化处理,消除量纲不同的影响;2)进行指标间相关性判断;3)求数据的协方差矩阵;4)求特征值、特征向量和累积贡献率;5)确定主成分因子;6)构建综合评价指数。
2.1 HVI指标的相关性分析
选取284种原棉的13项HVI指标值为对象,进行相关性分析,结果如表2所示。
表2中的数值代表了变量间的相关程度,绝对值越大,则相关性越强。可看出:成熟度指数(X2)与马克隆值(X1)、断裂比强度(X3)、断裂伸长率(X4)的相关系数分别达到了0.740、-0.512、-0.653;纺稳参数(X13)与断裂比强度(X3)、上半均长(X5)以及长度整齐度(X6)之间的相关系数分别为0.612、0.727、0.742,并且均在0.01水平上显著相关。由此可见,众多HVI指标间存在大量的信息重叠现象,因此,对其进行主成分分析可有效地剔除冗余信息,进而达到降低系统维数的目的,更合理地对原棉品质进行评价[4-5]。
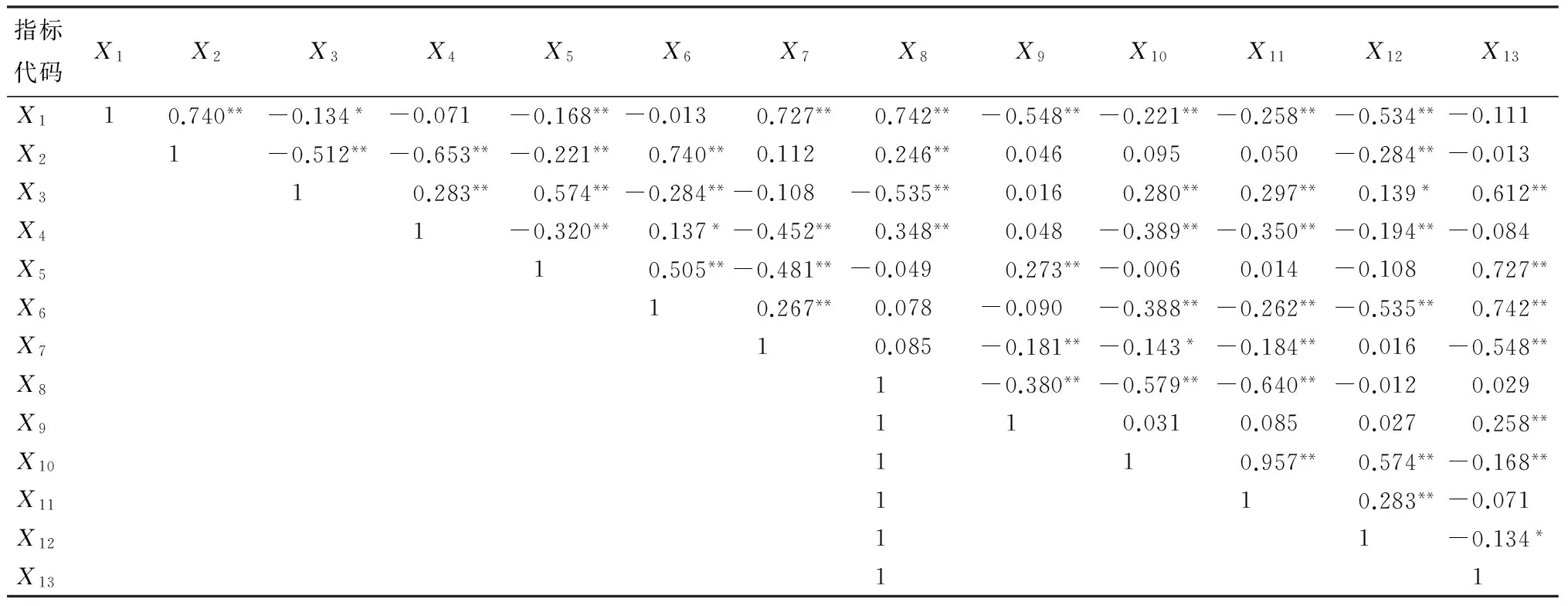
表2 HVI指标的相关系数Tab.2 Correlations among HVI indicators
注:* 表示在 0.05 水平(双边)上显著相关;** 表示在0.01 水平(双边)上显著相关。
2.2 主成分分析
利用MatLab对284种原棉的13项HVI指标数据进行主成分分析,表3、4分别示出主成分分析的方差分解特征提取表和初始因子载荷。 表3反映了提取出的各项主成分包含原始数据信息量的情况,累积贡献率表示前N个主成分合计提供的信息量占总体信息量的比例[6]。分析结果显示,前6项主成分的方差已经达到了总方差的88.51%,包含了原始样本的绝大部分信息,因此,选取前6项主成分作为原棉综合品质的评价因素。
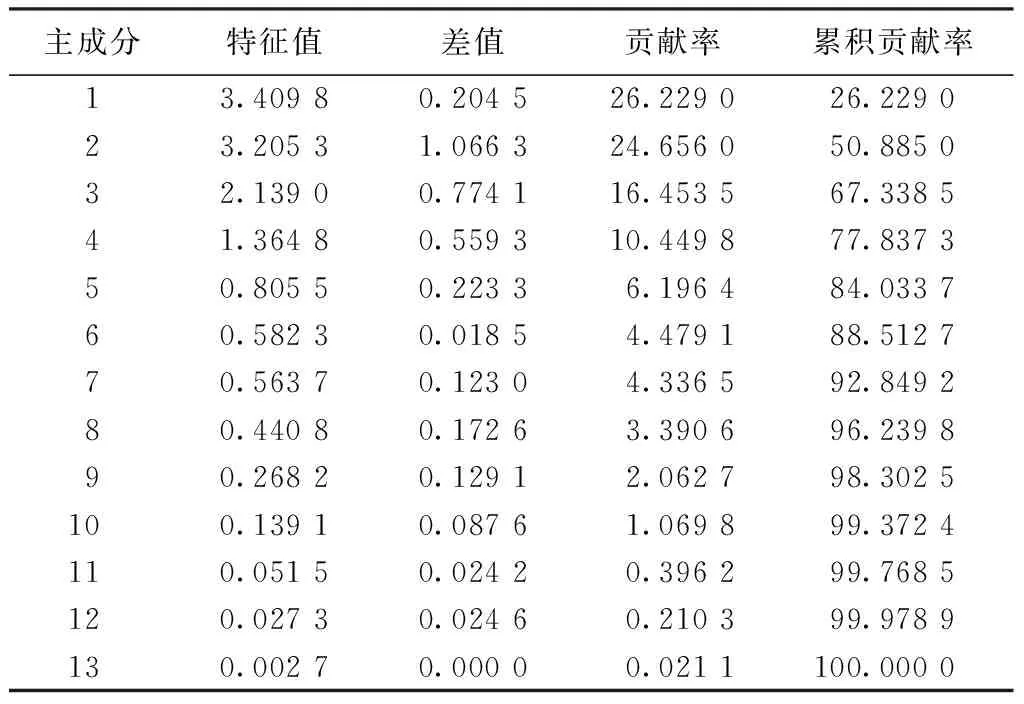
表3 方差分解特征提取分析表Tab.3 Total variance explained
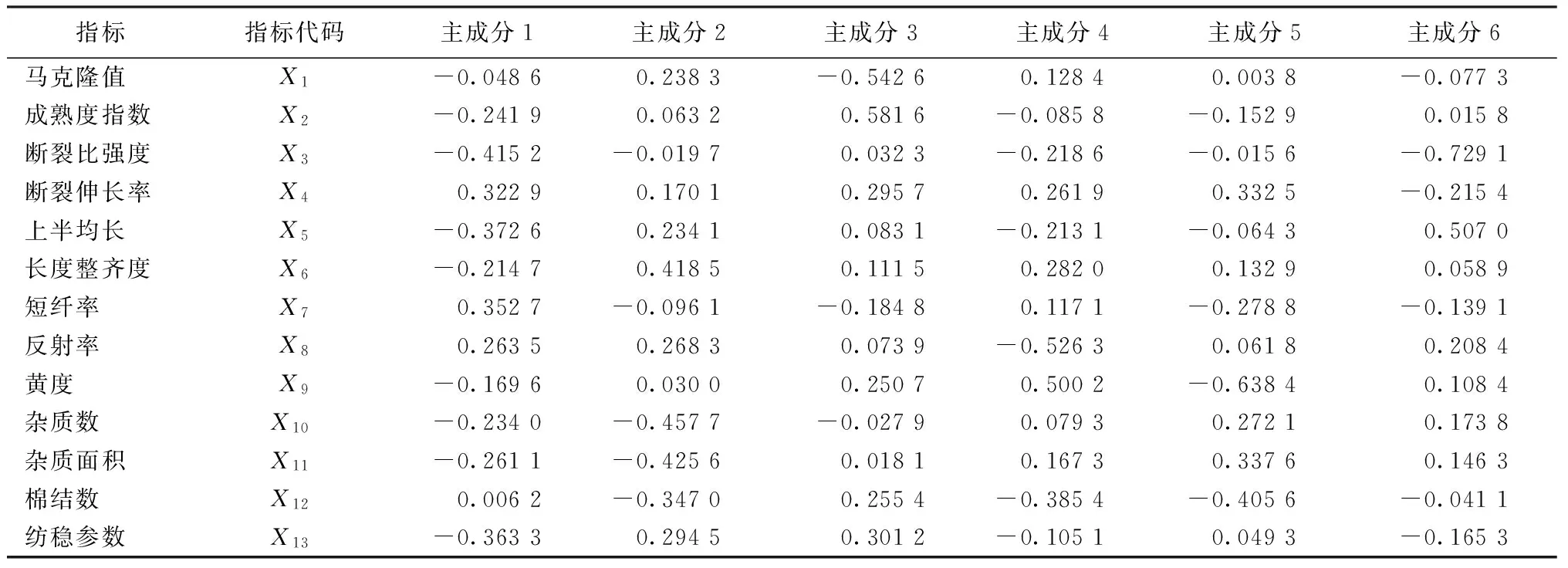
表4 初始因子载荷Tab.4 Loading of initial factors
初始因子载荷实质是指各项原始变量因子表达式的系数,反映原始指标对提取的主成分的影响程度,数值越高,表明该主成分包含该项指标越多的信息[7-8]。如表4所示,主成分3在马克隆值和成熟度指数上的载荷较大,说明主成分3对这2项指标具有较强的解释性;同理,主成分6较好地反映了棉纤维上半均长和断裂比强度这2方面特征。
将原始数据标准化后得到的矩阵与特征向量相乘,即可求得各项主成分的表达式[9-10]。通过对表3、4的数据进行分析,将表4的后6列分别与标准化后的数据相乘,得到的各项主成分表达式如下:
Y1=-0.363 3zx1-0.048 6zx2-0.241 9zx3-0.372 6zx4-0.214 7zx5+0.352 7zx6-0.415 2zx7+
0.322 9zx8+0.263 5zx9-0.169 6zx10-0.204 0zx11-0.261 1zx12+0.006 2zx13
Y2=0.294 5zx1+0.238 3zx2+0.063 2zx3+0.234 1zx4+0.418 5zx5-0.096 1zx6-0.019 7zx7+
0.170 1zx8+0.268 3zx9+0.030 0zx10-0.457 7zx11-0.425 6zx12-0.347 0zx13
Y3=0.301 2zx1-0.542 6zx2+0.581 6zx3+0.083 1zx4+0.111 5zx5-0.184 8zx6+0.032 3zx7+
0.295 7zx8+0.073 9zx9+0.250 7zx10-0.027 9zx11+0.018 1zx12+0.255 4zx13
Y4=-0.105 1zx1+0.128 4zx2-0.085 8zx3-0.213 1zx4+0.282 0zx5+0.117 1zx6-0.218 6zx7+
0.261 9zx8-0.526 3zx9+0.500 2zx10+0.079 3zx11+0.167 3zx12-0.385 4zx13
Y5=0.049 3zx1+0.003 8zx2-0.152 9zx3-0.064 3zx4+0.132 9zx5-0.278 8zx6-0.015 6zx7+
0.332 5zx8+0.061 8zx9-0.638 4zx10+0.272 1zx11+0.337 6zx12-0.405 6zx13
Y6=-0.165 3zx1-0.077 3zx2+0.015 8zx3+0.507 0zx4+0.058 9zx5-0.139 1zx6-0.729 1zx7-
0.215 4zx8+0.208 4zx9+0.108 4zx10+0.173 8zx11-0.146 3zx12-0.041 1zx13
式中zxi为xi(i=1,2,3,…,13)对应的HVI指标标准化后的数据。将各项主成分对应的特征值占总特征值的比例作为权重,加权求和6项主成分即可得到原棉品质综合评价函数Y,将其称为可纺性指数FSI,如下式所示。
Y=0.289 3Y1+0.278 6Y2+0.185 9Y3+
0.118 6Y4+0.07Y5+0.050 6Y6
式中,Y1,…,Y6分别表示由公式计算得到的6个主成分。本式中,可纺性指数可表示为6个主成分的线性函数,其系数值代表FSI与6个主成分Y1,…,Y6之间的相关性。
3 可纺性指数与部分评价指标的关系
3.1 可纺性指数与原棉等级的关系
为客观评价原棉品质,需要对可纺性指数FSI与原棉等级之间的关系进行研究,并与HVI指标中的纺稳参数SCI进行对比。其中,在HVI检测指标中SCI是反映原棉纺纱稳定性的指标,可衡量棉纤维的成纱强力。一般情况下,SCI的数值越大,纱线强力和纺纱过程的稳定性就越好。
对284种原棉的等级与其对应的SCI值作散点图,如图1所示。图中原棉等级与其对应的SCI值之间不存在直观的函数规律,难以通过划分SCI区间实现原棉等级的分类管理。同样对284种原棉与其对应的FSI值作散点图,如图2所示,可以发现二者之间存在较高的相关性。
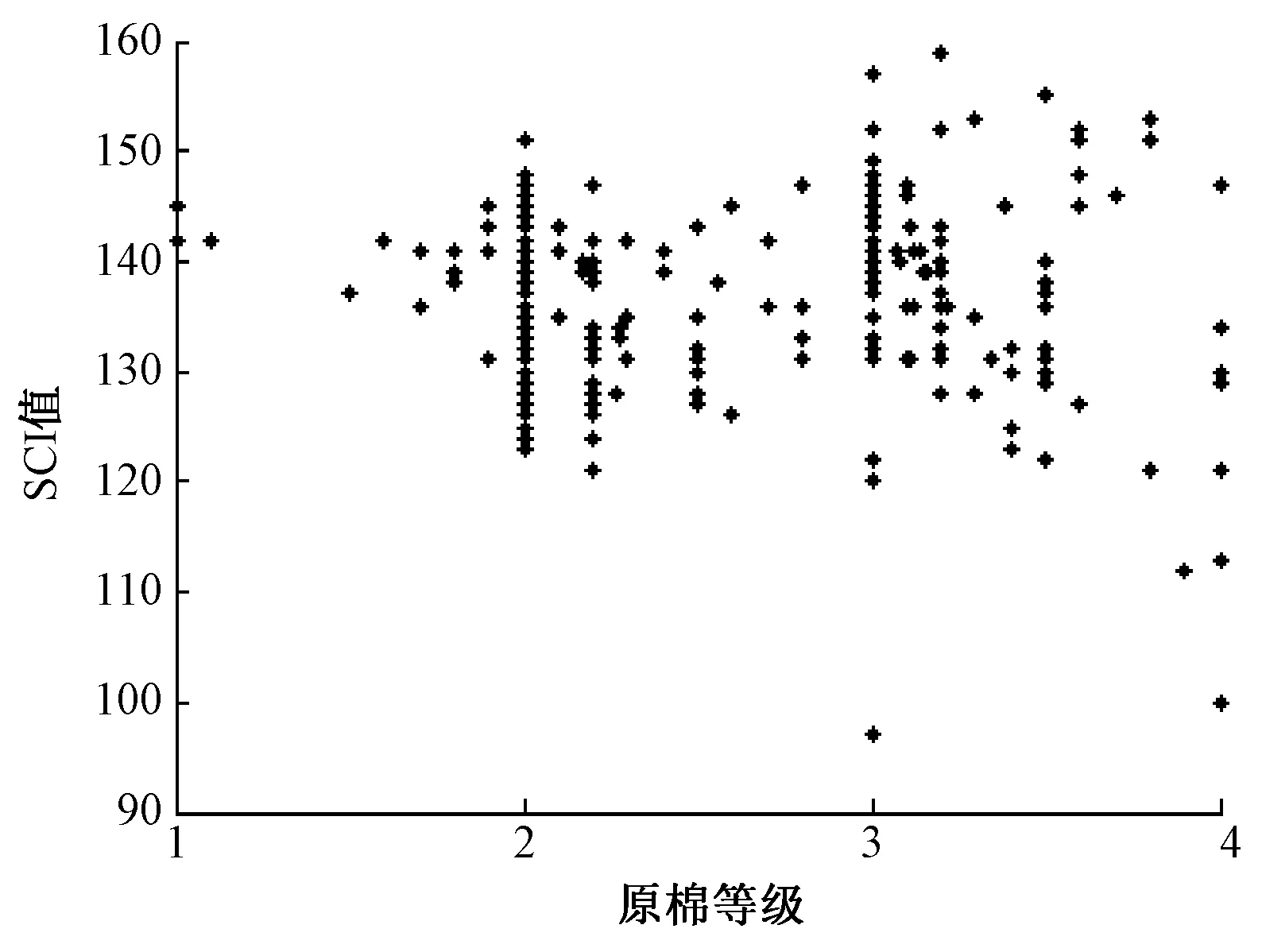
图1 原棉等级与SCI散点图Fig.1 Scatter of cotton grade and SCI
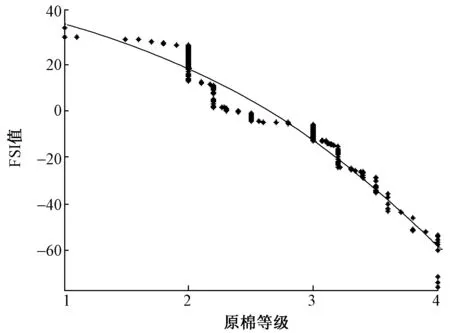
图2 原棉等级与FSI拟合曲线图Fig.2 Curve fitting diagram of cotton grade and FSI
观察图2可发现,随着原棉等级的增加,FSI数值逐渐减小,二者之间的关系可采用二次多项式函数对数据进行拟合[11],拟合方程为
f(x)=-6.782x2+2.046x+42.31
式中所示曲线方程可有效地表达原棉等级与FSI之间的函数关系,其拟合系数为0.948 6,因此,在原棉样本足够大的情况下,原棉等级可由其对应的FSI直接计算,即可通过划分FSI取值区间实现原棉等级的评定。
3.2 可纺性指数与成纱强力的关系
众所周知,纱线强力是衡量纱线综合品质的重要指标,因此有必要对可纺性指数FSI与棉纤维成纱强力之间的关系进行研究分析。
根据实际生产情况,从284种原棉中选择了139种,制订出45个配棉方案,并在环锭纺工艺下试纺18.2 tex(20个)和27.8 tex(25个)纯棉纱。为研究FSI及SCI与成纱强力的关系,分别对试纺纱线的强力值和对应原棉组的SCI加权平均值、FSI加权平均值进行数据拟合。结果表明:当拟合函数为二次多项式时,SCI与单纱强力的拟合精度最高;而对于FSI与单纱强力,采用指数函数对数据进行拟合则可达到最佳拟合效果,拟合曲线如图3~6所示。
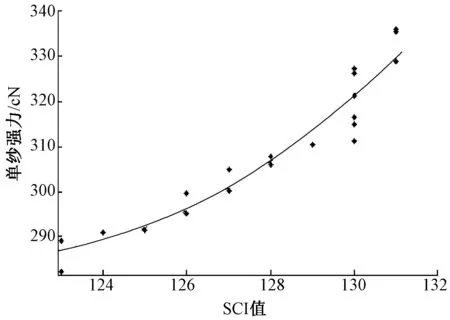
图3 SCI与18.2 tex纱线强力曲线拟合图Fig.3 Curve fitting diagram of SCI and strength of 18.2 tex yarn
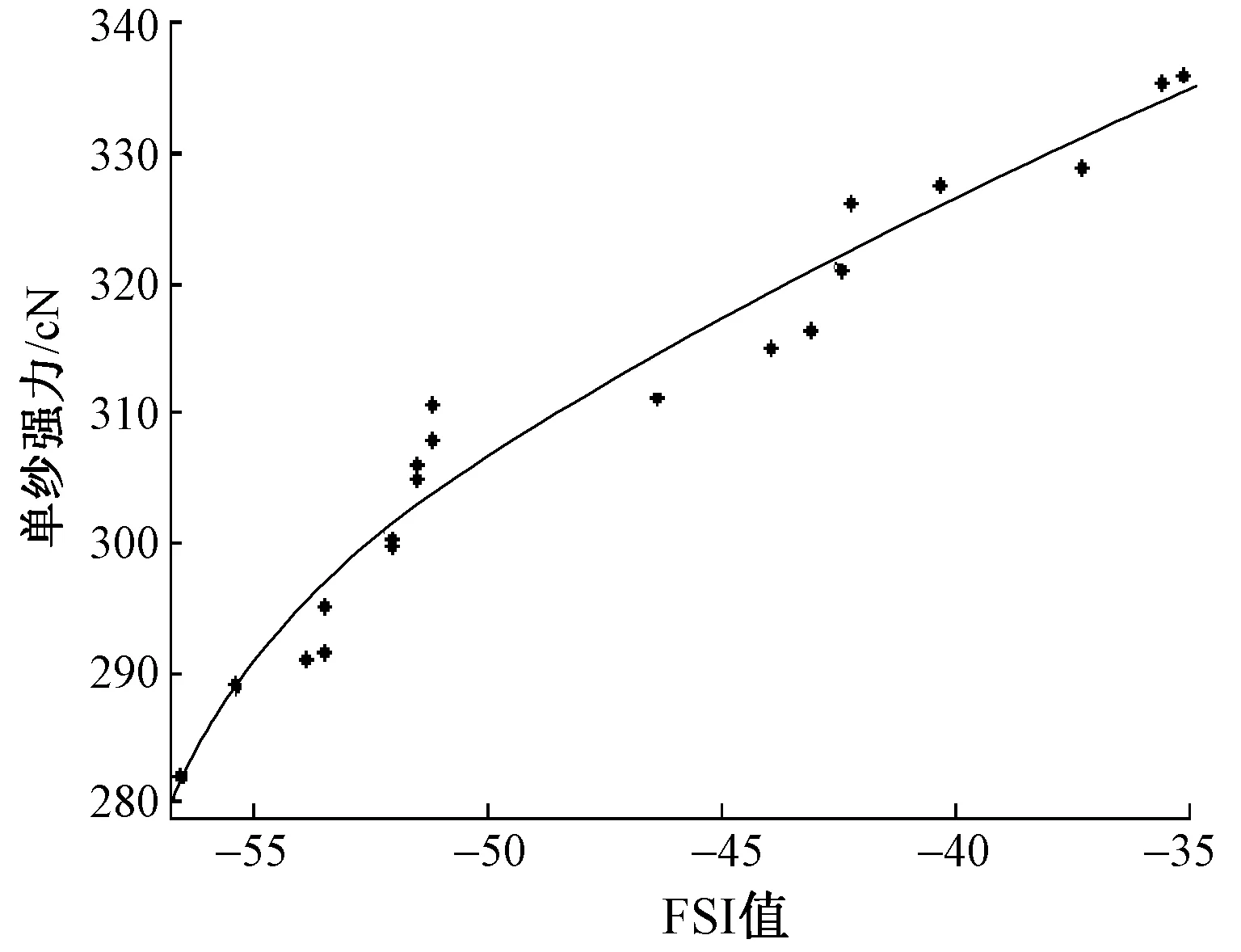
图4 FSI与18.2 tex纱线强力曲线拟合图Fig.4 Curve fitting diagram of FSI and strength of 18.2 tex yarn
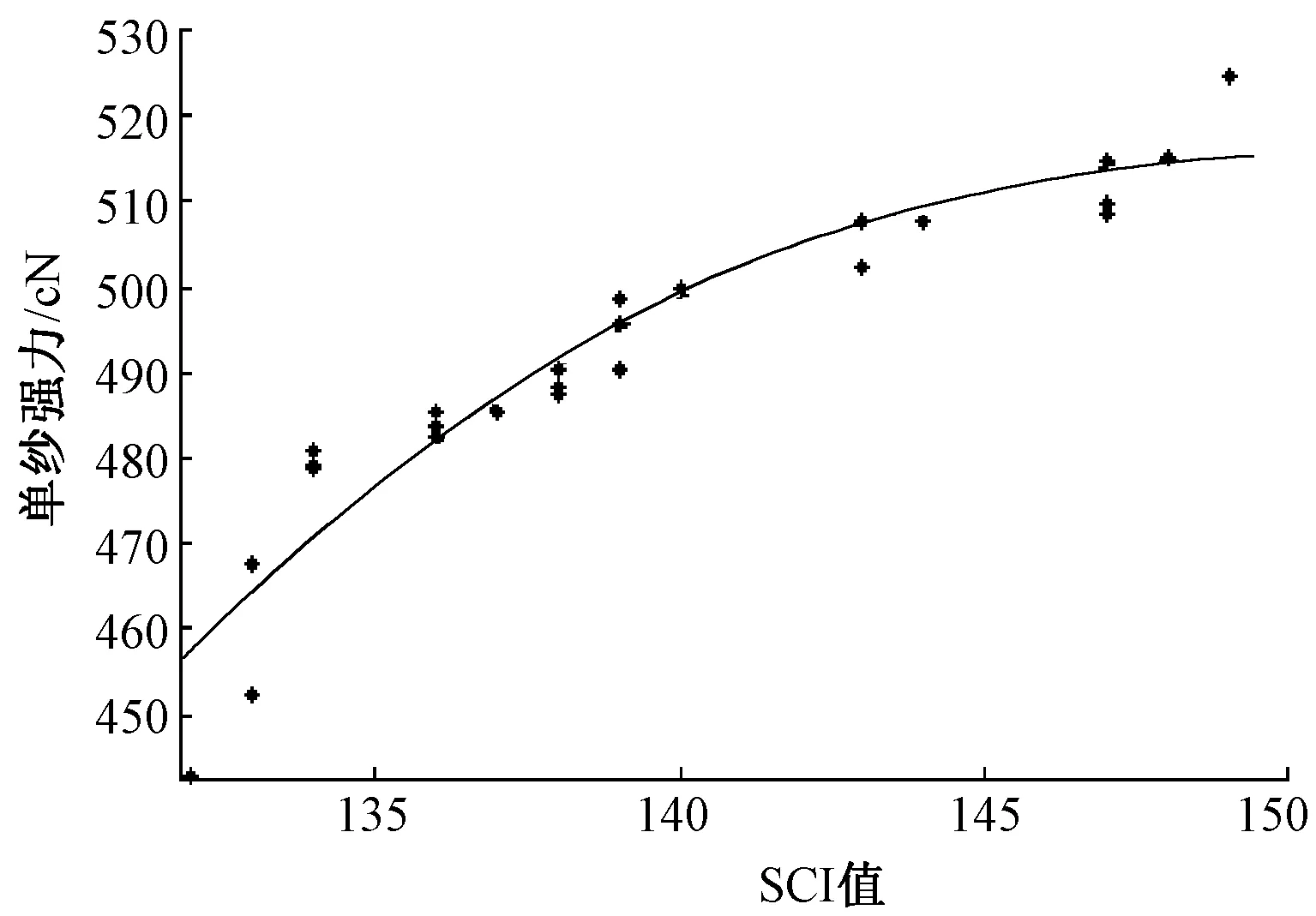
图5 SCI与27.8 tex纱线强力曲线拟合图Fig.5 Curve fitting diagram of SCI and strength of 27.8 tex yarn
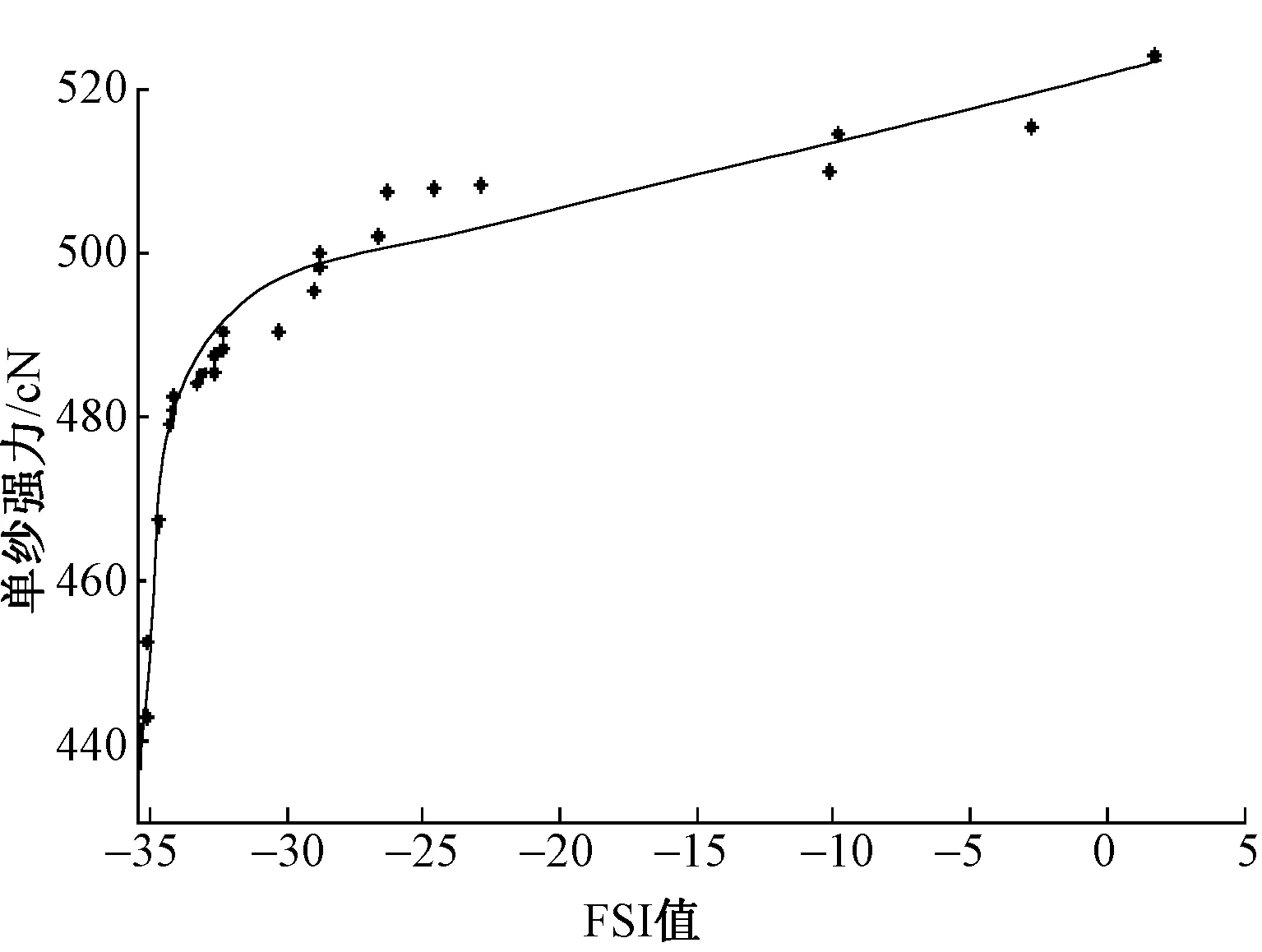
图6 FSI与27.8 tex纱线强力曲线拟合图Fig.6 Curve fitting diagram of FSI and strength of 27.8 tex yarn
由图3~6可知,原棉组的SCI加权平均值、FSI加权平均值越高,棉纤维的成纱强力就越高,二项指标均能较好地反映成纱品质。4种情形下的拟合方程如表5所示。就环锭纺18.2 tex纯棉纱而言,纺稳参数SCI、可纺性指数FSI与单纱强力之间拟合方程的拟合系数分别达到了0.923 4和0.957 6;对于环锭纺27.8 tex纯棉纱,SCI、FSI与单纱强力之间拟合方程的拟合系数分别达到了0.898 3和0.952 5,这表明,针对18.2 tex和27.8 tex纱线的强力,FSI的拟合效果更佳。 上述研究表明,可纺性指数FSI与纺稳参数SCI一样,均能够对棉纤维成纱强力进行高精度预测。

表5 拟合方程及其参数Tab.5 Parameters of fitting equations
4 结 论
本文将主成分分析法运用于原棉品质综合评价,利用包含绝大部分原始信息的主成分因子构建可纺性指数FSI,从而实现了原棉综合品质的定量化评价。经分析,纺稳参数SCI与原棉等级之间的相关性极小,几乎无规律可循,在实际生产中无法利用其对原棉进行分类管理。然而,可纺性指数FSI与原棉等级呈显著相关,可为原棉品质管理提供参考。此外,通过对比不同纱线产品的强力指标与对应原棉组的FSI和SCI加权平均值之间的相关性可知,FSI的预测精度及稳定性均优于SCI,可为纱线质量预测工作提供更有价值的参考。
[1] 石洋, 张得坤, 徐玫. 基于HVI检验数据的配棉方法[J].西安工程大学学报, 2011, 25(4):470-471. SHI Yang, ZHANG Dekun, XU Mei. Cotton assorting based on HVI data[J]. Journal of Xi′an Polytechnic University, 2011, 25(4):470-471.
[2] 刘国松, 邱兆宝, 汪黎明. 基于HVI数据的配棉主体变量选择[J]. 山东纺织科技, 2010(2):1-4. LIU Guosong, QIU Zhaobao, WANG Liming. Choice of main variables based on HVI data[J].Shandong Textile Science & Technology, 2010(2):1-4.
[3] 胡永宏.综合评价中指标相关性的处理方法[J]. 统计研究, 2002(3): 39-40. HU Yonghong. Approach of indexes correlation in comprehensive evaluation[J].Statistical Research, 2002(3):39-40.
[4] 张务建.原棉综合纺纱性能的模糊评判[J].五邑大学学报:自然科学版, 2002,16(4):64-66. ZHANG Wujian. Use of fuzzy mathmatics to appraise the spin capability of cotton [J]. Journal of Wuyi University: Natural Science Edition, 2002,16(4):64-66.
[5] 杨红英, 原海波, 周金利. 采用主成分分析法建立经纱可织性评价模型[J]. 棉纺织技术, 2011, 39(2):85-86. YANG Hongying, YUAN Haibo, ZHOU Jinli. Establishing warp weavability evaluation-model through principle component analysis[J].Cotton Textile Technology, 2011, 39(2):85-86.
[6] 汪祥莉, 孙琳.数理统计及其在数学建模中的实践[M].北京: 机械工业出版社, 2013:212-216. WANG Xiangli, SUN Lin. Mathematical Statistics and its Practice in Mathematical Modeling[M].Beijing: Machinery Industry Press, 2013:212-216.
[7] FENG Chung, KUO Jeffrey. The application of principal component analysis and gray relational method in the optimization of the melt spinning process using the cooling air system[J]. Textile Research Journal, 2013, 83(4):371-374.
[8] ZHENG Zhaohui, DU Hongbin. Muti-scale principal component analysis based on Matlab[J]. Journal of Dalian University of Technology, 2003, 43(4):428-430.
[9] 郭金, 董锁拽, 周文龙. 亚麻纱线USTER测试结果的主成分分析[J].浙江理工大学学报, 2012, 29(1):23-25. GUO Jin, DONG Suozhuai, ZHOU Wenlong. On the principal component analysis of the USTER test data of linen yarns[J]. Journal of Zhejiang Sci-Tech University, 2012, 29(1):23-25.
[10] 陆慧琴, 高月红.主成分聚类分析法在大学生综合测评中的应用[J].科技信息, 2010(26):80-81. LU Huiqin, GAO Yuehong. Principal component-cluster analysis in the comprehensive evaluation of college students[J]. Science & Technology Information, 2010(26):80-81.
[11] 刘霞, 王运锋. 基于最小二乘法的自动分段多项式曲线拟合方法[J].科学技术与工程, 2014(3):55-58. LIU Xia,WANG Yunfeng. Research on automatic segmentation based on least squares polynomial curve fitting method[J]. Science Technology and Engineering, 2014(3):55-58.
Construction of raw cotton spinnability index based on principal component analysis
GOU Jie, LIU Jianli, GAO Weidong
(KeyLaboratoryofEco-Textiles(JiangnanUniversity),MinistryofEducation,Wuxi,Jiangsu214122,China)
In order to realize the reasonable application of high volume instrument (HVI) indexes in the cotton quality evaluation and provide the guide for the cotton assorting, a comprehensive evaluation method of raw cotton based on principal component analysis was proposed. Firstly, 284 kinds of cotton from different areas and different levels were selected to subjected to the HVI detection. principal component analysis was performed on selected 13 indexes to eliminate the redundant information among the indexes. Secondly, the six extracted principal component factors were used for constructing the fiber spinnability index (FSI) to realize the quantitive evaluation of the raw cotton quality. Finally correlation on the FSI and yarn strength is discussed. The results showed that the FSI is higher, the higher yarn strength, and the better performance of the corresponding raw cotton. The comprehensive evaluation method of raw cotton based on principal component analysis achieved the quantitative evaluation of the cotton fiber spinnability, providing a reasonable reference for raw cotton quality management and yarn quality prediction.
raw cotton; quality evaluation; spinnability; principal component analysis; yarn strength
10.13475/j.fzxb.20140503206
2014-05-19
2015-04-14
国家自然科学基金青年科学基金项目(61203364);高等学校博士学科点专项科研基金项目(20120093130001)
苟捷(1989—),男,硕士生。主要研究方向为基于原棉品质参数的纱线质量预测。高卫东,通信作者,E-mail:gaowd3@163.com。
TS 104.1
A
