SHTB 加载紧凑拉伸试样断裂韧性测试仿真

邹广平，沈昕慧，赵伟玲，吴立夫，唱忠良

(1.哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨150001;2.黑龙江科技大学 现代制造工程中心，黑龙江 哈尔滨150022)

研究金属材料在动态加载下的断裂特性，不仅对指导金属材料构件的合理设计以保证其安全服役具有积极的意义，而且对研究在动态加载条件下裂纹的运动规律具有重要的学术价值［1］。然而与静态断裂问题相比，动态断裂问题在数学上和物理上都具有相当大的难度，因此对金属材料动态断裂韧性的研究尚未形成统一标准。目前材料动态断裂韧性测试装置多是基于Hopkinson杆装置研发［2］，按其应力波加载形式，可分为压缩应力波加载和拉伸应力波加载。压缩应力波加载实验装置主要是对Hopkinson压杆进行改造，试样以三点弯曲(3PB)为主，该装置最早由 Ruiz 等［3］提出，姜凤春等［4］用该方法对3PB试样进行了动态断裂韧性研究，但试样尺寸往往受制于Hopkinson杆的尺寸，且易出现试件与支撑点脱离的现象。相比较而言，基于拉伸应力波加载的紧凑拉伸(CT)试样，其试件尺寸小，容易满足平面应变条件，因此被广泛用于测量材料的断裂韧性和裂纹扩展速度。BEGUELIN等［5］利用试验机施加不同的加速度荷载加载紧凑拉伸试样，比较光弹实验与有限元结果，得到了试样动态响应与加载速率以及加载装置接触刚度之间的关系;BASSIM等［6］使用改进的分离式Hopkinson压杆上对紧凑拉伸试样进行加载，确定了在慢速、准静态和动态加载下的由J积分表示的断裂韧性的变化。邹广平等［7］改进的Hopkinson压杆装置，利用转换夹具的方法加载CT试样，同时用一种简单的弹簧质量模型来代表紧凑拉伸试样，获得了表征材料的动态断裂韧性的参量。

本文基于Hopkinson拉杆原理，针对紧凑拉伸试样，改变Hopkinson杆加载试样端的形状，使其可直接与试样相连，实现应力波加载下CT试样动态断裂韧性测试。利用ANSYS/LS-DYNA有限元软件，对CT试样断裂韧性测试实验过程进行了数值模拟，获得了CT试样在直接拉伸应力波加载下的动态响应。

1 冲击拉伸试验的数值模拟

1.1 试验方案概述

李玉龙等［8］改造Hopkinson拉杆实验装置研究了拉伸应力波加载下的中心切口I/II型裂纹试样的动态断裂问题，并研究了板中应力波的平衡条件。本文也采用该种方法，通过Hopkinson拉杆的杆端改进，使拉伸应力波直接对CT试样进行加载，且不需要夹具，试样与杆连接的方法是直接在Hopkinson入射杆和透射杆的连接端各切出一个凹槽，并在凹槽两侧上穿孔。将试样装卡在凹槽内，使用销穿过试样和入射杆、透射杆端的通孔，实现冲击拉伸过程中入射杆—试样—透射杆连接Hopkinson杆的改造方案如图1所示。紧凑拉伸试样的几何参数是按照国标GB4161-2007-T［9］设计的，B=6 mm，W=24 mm，a/W=0.5。图2表明了连接处的几何尺寸和连接方式。

图1 改进的Hopkinson实验装置及连接装置示意图Fig.1 Schematic of modified Hopkinson bar and connecting devices

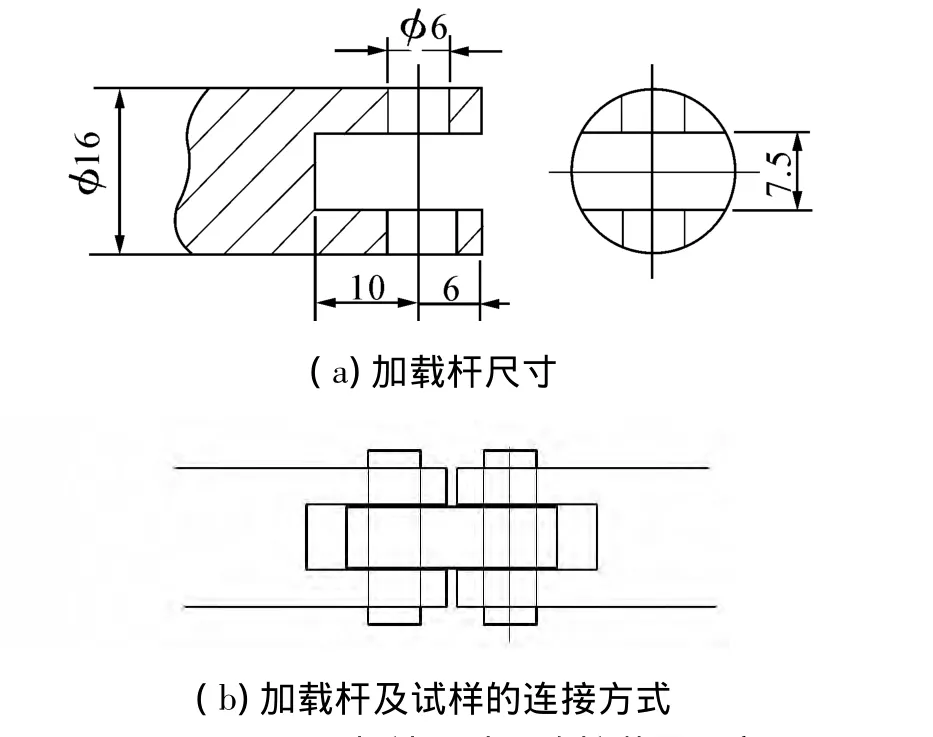
图2 Hopkinson杆端尺寸及连接装置示意图Fig.2 Schematic of dimensions of the waveguide bars and connecting devices

1.2 数值模拟的前处理

采用8节点显式动力分析单元SOLID164。根据问题的需要，采用了不同的材料模型。试验时认为Hopkinson杆是弹性的，传递应力波时应变率效应较为微弱，可将其忽略。这是Hopkinson拉杆压杆试验系统能将结构惯性效应和材料应变率效应解耦的前提之一。故将入射杆、透射杆和连接装置设定为各向同性弹性模型。考虑到紧凑拉伸试样在受载时的塑性变形，采用双线性随动材料模型，利用单元失效的方法模拟开裂，设定其材料为率无关材料LYl2cz铝合金，材料参数可以由准静态试验测得，其弹性模量为 68.3 GPa，切线模量为 88.1 MPa，失效应变为 0.18。

考虑到结构的对称性，建模时只选取整体结构的一半。建模完成后，对入射杆和试样截面进行简单的分割，便于划分网格，得到如图3的有限元模型。透射杆的有限元模型可由入射杆有限元模型通过VSYMM对称操作生成，最终形成整个结构的有限元模型。夹具与试样和Hopkinson杆的连接处采用自动面面接触算法。

图3 三维有限元模型图Fig.3 The 3-D finite element model

1.3 加载和求解

利用Hopkinson拉杆实验装置进行加载时，撞块以一定速度与固定于入射杆末端的挡块发生撞击，入射杆中会形成的拉伸应力波。根据一维应力波分析，拉伸波在入射杆中传播时各点的波形是相同的。为了简化分析过程，本文忽略撞击和产生拉伸波时的复杂情况，直接在入射杆模型的自由端施加一个拉伸波波形。本文中施加的载荷曲线是依照试验中波形整形后的应力波曲线建立的。然后将载荷曲线作为应力载荷施加在入射杆端的受载单元组元上。加载应力波时间-应力曲线如图4所示。

图4 应力波加载曲线Fig.4 The curve of loading stress wave

2 数值模拟结果

2.1 试样的承载过程

通过LS-PREPOST可以观察求解的动态结果。从全局的求解结果可以看出:拉伸波从入射杆的末端传至试样，然后又沿着透射杆继续传播。将试样部分放大后，可以看到试样承受从开始应力波载荷，直至裂纹开始扩展的过程的应力云图，如图5所示。其中图5(c)、(d)试样已开裂。

图5 试样承载过程Fig.5 The loading process of specimen

2.2 入射波、反射波和透射波的波形

通过曲线查看入射杆和透射杆杆中间单元的计算结果，得到了入射、反射和透射波，如图6所示。

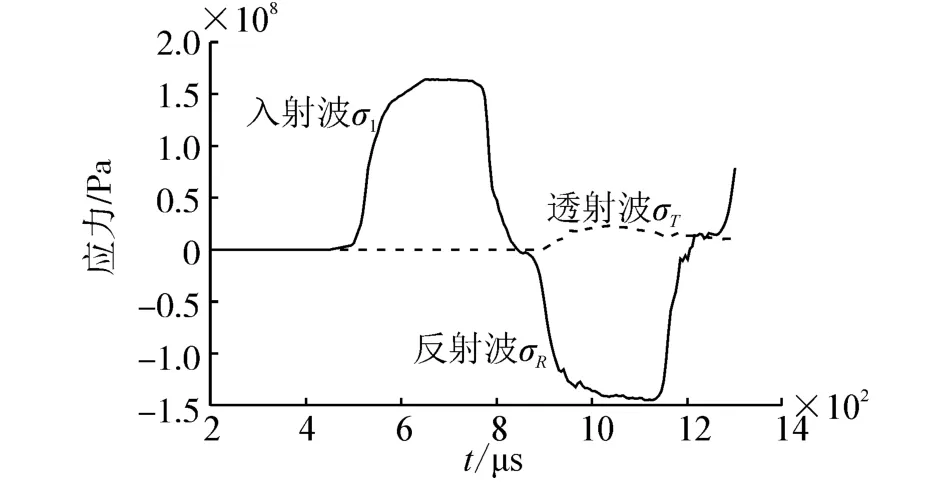
图6 入射波、反射波和透射波波形Fig.6 The waveforms of incident wave，reflection wave and transmitted wave

若将反射波和透射波叠加，即σT-σR，可以得到图7所示的曲线。

实验数据说明，通过在Hopkinson拉杆实验装置入射杆和透射杆的连接端切槽的方式，对小尺寸紧凑拉伸试样进行冲击拉伸加载的过程是符合一维应力波假设的，同时也验证了仿真的有效性。这样，可以根据Hopkinson杆加载的一维试验原理计算出t时刻试样内的平均应力σs(t)。当试样中裂纹发生扩展时，随着应力的释放，平均应力σs(t)的曲线会在起裂时刻发生骤降。以上分析说明，在试验中通过测定入射波、反射波和透射波的波形来确定起裂时间是可行的，这对于指导实验进行具有积极意义。

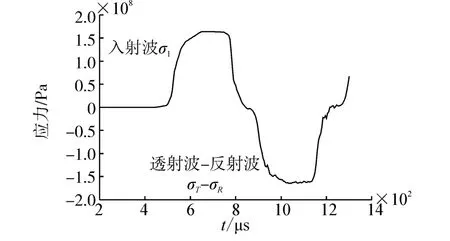
图7 入射波，透射波与反射波相减得到的曲线Fig.7 The curve of incident wave，and the subtracion result by transmitted wave and reflection wave

2.3 应力波在试样中的传播

通过观察加载过程中各个时刻试样中的应力场分布，可以得到应力波在试样中的传播规律，从而可以相对精确地确定试样达到动态平衡所需的时间。通常该时间是与试样的连接装置以及加载时应力波的波形有关，对试样达到动态平衡所需的时间进行研究，有助于选择加载波形和实验装置的改进。选取试样厚度方向的对称截面进行观察，得到结果如图8。由图8可见，应力波在与入射杆相连的销接触试样后开始传入试样，绕过裂尖向与透射杆相连的销传去。开始时应力场在试样上分布是非对称的，一段时间后逐渐达到对称分布的状态。

图8 应力波在试样中的传播Fig.8 The propagation of stress wave in CT specimen

3 结果分析

3.1 应力平衡分析

在Hopkinson杆加载的断裂试验中要得到可靠的断裂韧性，必须满足2个基本假设，即一维应力波，应力平衡。本节通过对试样裂尖两端单元的应力分析(图9)和试样与入射杆和透射杆接触两端的动载荷比较结果(图10)，研究在该实验装置加载条件下试样的应力平衡情况。

图9是试样裂尖左右两端单元的应力结果图。从图中可以看出:在685 μs时，试件开始受载;大约在770 μs时，裂尖左右两端单元达到了应力平衡;应力波传入试样到试样达到动平衡经历的时间约为85 μs。而 CT 试样的起裂时间在约 865 μs，此时试样已经处于应力平衡状态。因此在此加载条件下得到的试样的断裂韧性是可靠的。图10为试样左右两端动载荷曲线，其中PI为入射杆加载点与试样之间的动载荷，PII为试样与透射杆之间的动载荷。其计算公式为:PI=EA(εI+εR)，PII=EAεT，E 和 A 分别为Hopkinson杆的弹性模量和横截面积，εI、εR和εT分别为测得的入射波、反射波和透射波的应变值。从图中可以得到与图9相似的结果，即大约在770 μs时，试样左右两端达到了应力平衡，应力波传入试样到试样达到动平衡经历的时间约为85 μs。

图9 试样裂尖左右两端单元的应力结果图Fig.9 The result curves of left and right CT specimen crack elements

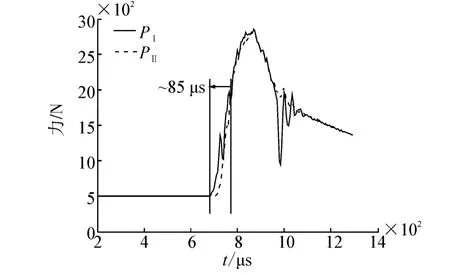
图10 动载荷加载曲线Fig.10 The dynamic loading curve

通过2种方法对应力平衡的验证，说明了该实验测试试样的动态断裂韧性方法的有效性，试样起裂发生在试样应力平衡后，满足Hopkinson杆假设，因此准静态断裂理论在该实验条件下是可以应用的。

3.2 动态J积分的计算

本文使用Kishimoto［10］提出的动态J积分计算式。在直角坐标下将其表示为

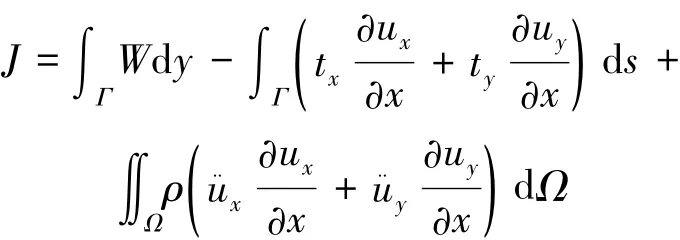
式中:W为应变能密度;Γ为围绕裂纹尖端选取的任意围线，如图11所示;Ω为Γ和裂纹面所包围的面积;tx、ty分别为 x、y 方向的面力分量，ux、uy和分别为位移和加速度矢量在x、y方向的分量。

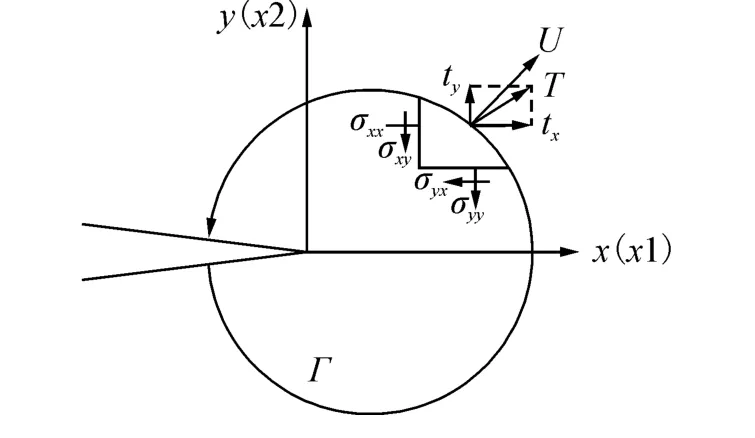
图11 J积分定义的区域Fig.11 J-integral region

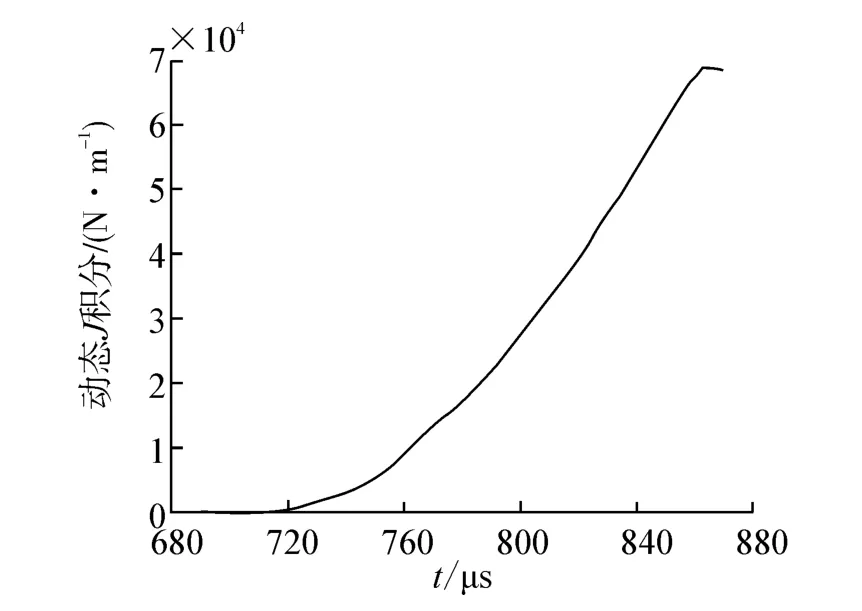
图12 JI(t)曲线Fig.12 The curve of JI(t)

图13KI(t)曲线Fig.13 The curve of KI(t)

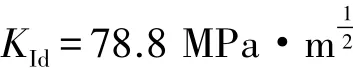
4 结论

本文对Hopkinson拉杆实验装置进行了改进，采用ANSYS/LS-DYNA有限元软件，对拉伸应力波加载CT试样的动态断裂过程进行了数值仿真，获得结论如下:

1)对提出一种新的测试紧凑拉伸试样动态断裂韧性方法进行了有限元验证，获得了基于Hopkinson杆加载的紧凑拉伸试样的动态断裂行为。

2)研究了应力波加载时CT试样的应力平衡问题和起裂时间以及应力波在CT试样中的传播过程，证明了该种加载方式可以较好的满足一维应力波假设，试样在起裂之前已经达到了应力平衡状态。

3)通过采用动态J积分计算方法，对LY12cz铝合金CT试样的断裂韧性进行了计算，结果与文献［11］相符合，从而论证了改进方案的可行性，为后续基于拉伸应力波加载的CT试样断裂韧性实验研究提供依据。

［1］邹广平.金属材料动态断裂韧性的表征与测试［D］.哈尔滨:哈尔滨工程大学，2005:7-12.

ZOU Guangping.Characterization and measurement of metals dynamic fracture toughness［D］.Harbin:Harbin Engineering University，2005:7-12.

［2］JIANG F，VECCHIO K S.Hopkinson bar loaded fracture experimental technique:a critical review of dynamic fracture toughness tests［J］.Applied Mechanics Reviews，2009，62(6):060802.

［3］RUIZ C，MINES R A W.The Hopkinson pressure bar:an alternative to the instrumented pendulum for Charpy tests［J］.International Journal of Fracture，1985，29(2):101-109.

［4］JIANG F，VECCHIO K S.Experimental investigation of dynamic effects in a two-bar/three-point bend fracture test［J］.Review of Scientific Instruments，2007，78(6):063903.

［5］BEGUELIN P，FOND C，KAUSCH H H.The influence of inertial effects on the fracture of rapidly loaded compact tension specimens part A:loading and fracture initiation［J］.International Journal of Fracture，1998，89(1):85-102.

［6］BASSIM M N，BAYOUMI M R，SHUM D.Study of the variation of fracture toughness with loading rate using compact tension specimens［J］.Engineering Fracture Mechanics，1987，26(4):619-623.

［7］邹广平，唱忠良，曲嘉，等.平面应变下紧凑拉伸试样的动态断裂韧性研究［J］.实验力学，2011，26(3):240-246.

ZOU Guangping，CHANG Zhongliang，QU Jia，et al.Experimental study of dynamic fracture toughness of specimen subjected to compact tension under plane strain［J］.Journal of Experimental Mechanics，2011，26(3):240-246.

［8］XU Z，LI Y.A novel method in determination of dynamic fracture toughness under mixed mode I/II impact loading［J］.International Journal of Solids and Structures，2012，49(2):366-376.

［9］GB/T21143-2007.金属材料准静态断裂韧度的统一试验方法［S］.北京:中国标准出版社，2008.

［10］KISHIMOTO K，AOKI S，SAKATA M.Dynamic stress intensity factors using J-integral and finite element method［J］.Engineering Fracture Mechanics，1980，13(2):387-394.

［11］XIA Y，RAO S，YANG B.A novel method for measuring plane stress dynamic fracture toughness［J］.Engineering Fracture Mechanics，1994，48(1):17-24.