二维狭缝内波动基频共振频率的解析分析

丛龙飞，滕斌，勾莹

(大连理工大学海岸与近海工程国家重点实验室，辽宁大连116024)

近年来超大型浮体在海洋工程中得到广泛应用，这种结构形式将多个浮体进行连接，因此在各个模块之间存在狭缝，当狭缝具有某种尺度时，狭缝内部水体会产生巨大的波动。对可能产生使狭缝水体共振的入射波浪频率进行计算对工程实际具有很大意义。MOLIN B［1-2］在浮体尺度无穷大，无穷水深假设下对二维及三维月池内水体的共振频率进行了研究，结果可以直接应用到二维狭缝的分析;MIAO Guoping等［3］应用匹配渐进展开方法得到了狭缝的共振频率，提出了小狭缝情况下共振频率的解析表达式;FALTINSEN O M等［4］应用线性势流理论对二维月池进行了分析，考虑了粘性的影响并与实验结果进行了对比;朱仁传等［5-6］应用线性势流理论对小间隙对浮体水动力特性的影响进行了数值分析，通过频域计算得到共振频率;SUN Liang等［7-8］对方箱间狭缝的共振问题进行了三维分析;SAITHO T等［9］对二维狭缝问题进行简化，得到了狭缝内水体的共振频率并与实验结果进行了对比;LU Lin等［10-12］通过求解N-S方程对狭缝共振现象进行了研究，与势流结果进行了对比并讨论了狭缝内水体波动的能量耗散;KRISTIANSEN T等［13-15］将势流模型与粘性流模型进行耦合，对狭缝共振问题进行了深入研究;LIU Yong等［16］利用线性势流理论特征展开方法，在狭缝内部区域引入阻尼项，对狭缝水体的波动进行了解析研究;ZHANG Xinshu等［17］利用线性势流理论特征展开方法对两层流体下的月池共振问题进行了研究。

本文对二维方形结构间的狭缝进行分析，对狭缝内部水体进行“刚体”假设，进而对其共振频率进行求解。在得到狭缝“刚体”水动力系数的过程中与高阶边界元方法所得结果进行了比较，验证了本文方法的正确性。共振频率的计算结果表明，本文方法对各种尺度狭缝内部水体共振频率的求解均适用。

1 控制方程与问题简化

考虑波浪与固定于水面上2个相同方箱的作用问题，方箱吃水为T、宽度为B，箱体间狭缝宽度为2a，水深为d。取二维笛卡尔直角坐标系OXZ，Z向上为正，X向右为正，坐标原点O位于静水面狭缝中心处，如图1。

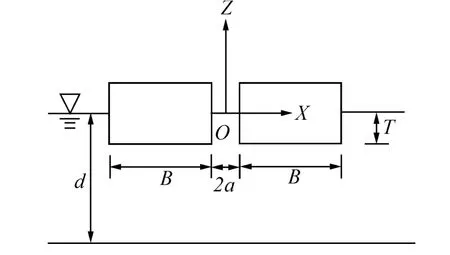
图1 计算域定义图Fig.1 Definition of the computation domain

在不可压缩理想流体初始无旋的假设下，整个流域存在满足Laplace方程的速度势Φ，考虑规则波浪与箱体作用的稳态问题，可分离出时间因子:

复速度势φ仍满足Laplace方程。假设狭缝宽度为小量，在狭缝内部对空间变量、速度势函数进行无量纲化:x'=x/a，z'=z/T，φ'=φ/aTω。则 Laplace方程变为

因此可以得到

式(1)表明狭缝内水体的水平速度u沿水平变化相比于垂向速度v沿垂向变化是小量，结合边壁法向速度为零的条件，狭缝内部水体的水平速度可以忽略，即u=0，由Laplace方程得

式(2)说明狭缝内部水体有相同的垂向速度，像“刚体”一样。这样可以对狭缝内部水体的波动形式进行简化，将其视为质量为M=2ρaT的刚体，原问题就变为波浪作用下两箱体间单浮体的响应问题。

2 狭缝内水体波动的解析分析

如前文所述，可以将狭缝内的水体视为质量为M做上下升沉运动的“刚体”，如图2(a)。图2(b)是狭缝“刚体”的受力分析。其中Fb、Fw和Ff分别为狭缝“刚体”底部受到的静浮力、波浪激振力和辐射力。

图2 问题简化图Fig.2 Sketch of the simplification

设狭缝“刚体”的运动位移为

Ξ =Re［ξe-iωt］

则底部静浮力Fb可按初始吃水和水体运动位移分解为

辐射力Ff可表示为狭缝“刚体”运动的水动力系数与其运动幅值的乘积关系:

式中:m(ω)和b(ω)分别为狭缝“刚体”运动的附加质量和辐射阻尼。

狭缝“刚体”的运动方程为

代入各项表达式并消除时间因子，得

狭缝“刚体”的运动响应为

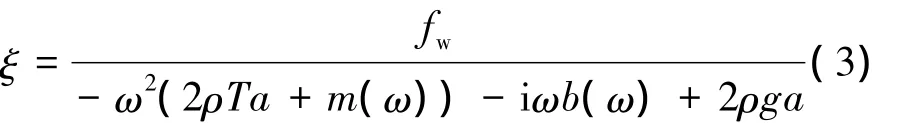
式(3)表明，狭缝“刚体”的运动位移幅值与其运动产生的水动力系数有密切关系。在使式(3)分母的绝对值取极小值，该频率下狭缝内水体的运动响应会接近极大值，此时即产生了共振现象。

求解该方程的核心是狭缝“刚体”附加质量和辐射阻尼的求解，下面将对二者进行分析和求解。

3 狭缝水动力系数的求解

考虑两相同箱体间狭缝“刚体”做单位垂向运动，由于问题的对称性，可将x=0处视为固壁，取一半结构进行简化，如图3。

图3 简化后的计算域Fig.3 Simplification of the computation domain

分解流域成3个子域，各子区域的边界条件如下:

子区域I:

子区域II:

子区域III:

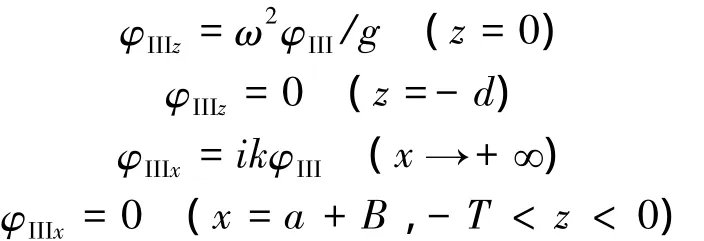
I、II区域的连续条件:

II、III区域的连续条件:

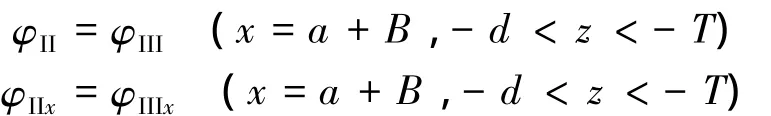
对于子区域I，速度势为满足上边界为齐次边界条件的通解和一个满足上边界非齐次边界条件的特解之和:

式中:Ak为待定系数，特征值为μk=kπ/(d-T)(k=0，1，…)，垂向特征函数为

对于子区域II，利用上下底的齐次边界条件，速度势可以表达为

式中:Bk和Ck为待定系数。

对于子区域III，利用水底的齐次边界条件、水面的自由水面条件以及无穷远场的远场条件，速度势可以表达为

式中:Dk为待定系数，特征值k0和kj(j=1，2，…)为下述色散关系的解:

垂向特征函数为

利用x=a处的速度势和水平速度的匹配条件，可得

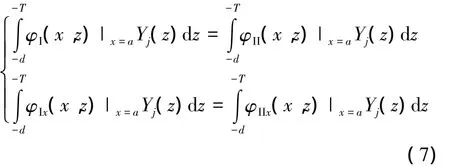
对I区和II区速度势截断至有限项NI、NII得

利用x=a+B处的速度势和水平速度的匹配条件，可得

求解式(8)、(10)所得方程组，可确定各区域速度势的展开系数，方程组中系数可将式(4)～(6)代入式(7)、(9)得到。

求得各区域速度势的展开系数后利用伯努利方程，将所得压强沿狭缝“刚体”底面积分可得狭缝“刚体”底部受到的辐射力为

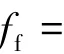
对于II区和III区的速度势截断至有限项NII、NIII得

狭缝“刚体”运动产生的附加质量和辐射阻尼为:m(ω)=Re(ff)/ω2，b(ω)=Im(ff)/ω。

4 狭缝水动力系数的计算结果与对比

为了验证本文方法的正确性，将本文求得的狭缝“刚体”水动力系数与高阶边界元方法所得结果进行对比。图 4是方箱宽 B/d=1.0、吃水 T/d=0.3、缝宽2a/d=0.02时狭缝“刚体”的附加质量和辐射阻尼系数，无量纲化参数的定义为:m'=m/ρad，b'=b/(ρa(gd)0.5)。二者结果吻合良好，证明了本文方法的正确性。

图4 狭缝“刚体”辐射阻尼与附加质量的计算结果对比(B/d=1.0，T/d=0.3，2a/d=0.02)Fig.4 Results comparison of added mass and damp(B/d=1.0，T/d=0.3，2a/d=0.02)

从图4中可以看到，狭缝“刚体”的附加质量随波数的变化较为平缓，狭缝“刚体”的附加质量随波数增大而增大，辐射阻尼随波数增大而减小。

图5及图6为ω=3.50 rad/s时狭缝“刚体”附加质量、辐射阻尼随狭缝宽度的变化曲线与二者随吃水深度的变化曲线。

从图5及图6中可以看出，狭缝“刚体”附加质量与辐射阻尼随狭缝宽度增大而变大，与狭缝宽度为超线性关系;狭缝“刚体”的附加质量在大吃水深度时随吃水深度增大而剧烈变大，辐射阻尼随吃水深度增大而下降，但与附加质量相比变化并不明显。

图5 狭缝“刚体”附加质量、辐射阻尼随狭缝宽度的变化(ω=3.50 rad/s，T/d=0.2，B/d=1.0)Fig.5 Added mass and damp with different widths of the gap(ω=3.50 rad/s，T/d=0.2，B/d=1.0)

图6 狭缝“刚体”附加质量、辐射阻尼随吃水深度的变化(ω=3.50 rad/s，2a/d=0.02，B/d=1.0)Fig.6 Added mass and damp with different draught(ω=3.50 rad/s，2a/d=0.02，B/d=1.0)

5 狭缝内水体共振频率的求解与对比

由式(3)可得，狭缝内波动的共振频率由式(3)分母实部为零的条件决定。阻尼对共振频率的影响较小，阻尼的影响主要体现在共振情况下振动幅值的大小。这样，在估算狭缝内波动共振频率时，可忽略辐射阻尼的影响。

在以下计算中，忽略狭缝“刚体”的辐射阻尼，对下式采用迭代方法对共振频率进行估算:

数值计算表明，由于狭缝“刚体”附加质量随频率的变化不大，迭代计算只需几次便可收敛。图7为应用本文方法计算结果与文献［3，9，16］结果的对比。

图7 共振频率的计算结果对比(B/d=1.0，T/d=0.2)Fig.7 Results comparison of resonance frequency(B/d=1.0，T/d=0.2)

计算结果表明:1)应用本文方法计算所得结果与文献［16］所得结果吻合良好。2)在小狭缝时，其他文献的简化方法与本文方法、文献［16］的结果比较接近;而在大狭缝时，与文献［16］的结果有较大差异，同时各文献结果在大狭缝时也相差较大，这是由于各文献对狭缝内部波动及外流场采用不同简化导致的:①文献［9］将狭缝内部水体与外部水体视为连通器，同时假设狭缝与外部流场之间水体为均匀流动，与实际情况有很大差别，故结果与文献［16］有差距;②文献［3］提出的公式是在狭缝尺度趋于0时的渐进结果，在小狭缝时，与本文结果以及文献［16］的结果吻合良好，在大狭缝的情形，小狭缝假设不成立，故与文献［16］的结果有差距;③对于文献［3］和文献［9］，由于二者的假设条件不同，故二者的结果之间有差距;④另外文献［3］与文献［9］相比，其假设更接近实际情况，故其结果与本文结果以及文献［16］的结果更为接近。对比表明本文方法适用的范围更宽，适用于小狭缝及大狭缝问题。

图8为本文方法与文献［6］应用比例边界元法计算结果的对比，对比结果良好。

对比结果表明，本文方法与文献［6］的比例边界元方法以及文献［16］的线性势流半解析解所得结果在具体数值和随狭缝参数的变化趋势方面均吻合良好，这说明对于小狭缝和大狭缝，本文方法与其他文献的简化方法相比更接近实际，对于不同尺度的狭缝内水体波动问题均能得到准确的共振频率。

对于小狭缝，通过上节给出的数值结果，可以对其共振频率在狭缝尺度趋于0时的特征进行描述，由图 6可以看出 m∝ak(k＞1.0)，结合式(12)，有

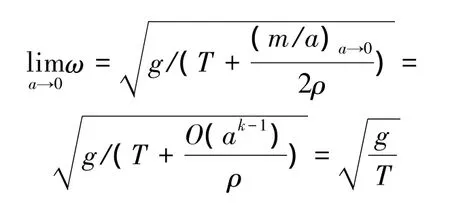
该结果与文献［3，9］在小狭缝时的近似一致。

图8 共振频率的计算结果对比(B/d=1.0，2a/d=0.01)Fig.8 Results comparison of resonance frequency(B/d=1.0，2a/d=0.01)

6 结论

本文将波浪作用下二维狭缝内水体波动转化为波浪作用下单浮体的响应问题;应用线性势流理论特征函数展开方法对波浪作用下狭缝内水体波动的共振频率进行了计算与分析，讨论了狭缝内水体共振的机理。通过本文的计算与分析可以得到下述结论:

1)计算狭缝共振频率时，可以将狭缝内水体简化为“刚体”;

2)狭缝内水体的波动幅值主要由狭缝“刚体”的水动力系数决定;

3)狭缝共振频率主要由狭缝“刚体”的附加质量决定;

4)狭缝内水体的共振频率随狭缝宽度增大而减小;

5)狭缝内水体的共振频率随吃水深度增大而减小;

6)对于小宽度的狭缝，狭缝内水体的共振频率接近于(g/T)0.5(g为重力加速度，T为箱体吃水深度)。

［1］MOLIN B.On the piston mode in moonpools［C］//14th Int Workshop on Water Waves and Floating Bodies.Michigan，1999:103-106.

［2］MOLIN B.On the piston and sloshing modes in moonpools［J］.Journal of Fluid Mechanics，2001，430:27-50.

［3］MIAO Guoping，ISHIDA H，SAITHO T.Influence of gaps between multiple floating bodies on wave forces［J］.China Ocean Engineering，2000(4):407-422.

［4］FALTINSEN O M，ROGNEBAKKE O F，TIMOKHA A N.Two-dimensional resonant piston-like sloshing in a moon pool［J］.Journal of Fluid Mechanics，2007，575:359-397.

［5］朱仁传，缪国平，尤云祥，等.小间隙对多浮体系统水动力性能的影响［C］//第七届全国水动力学学术会议暨第十九届全国水动力学研讨会文集(下册).北京:海洋出版社，2005:175-182.

ZHU Renchuan，MIAO Guoping，YOU Yunxiang，et al.Influences on hydrodynamics of multiple floating structures with small gap in between［C］//Proceedings of the 7th National Congress on Hydrodynamics and 19th National Conference on Hydrodynamics.Beijing:China Ocean Press，2005:175-182.

［6］滕斌，何广华，李博宁，等.应用比例边界有限元法求解狭缝对双箱水动力的影响［J］.海洋工程，2006(2):29-37.

TENG Bin，HE Guanghua，LI Boning et al.Research on the hydrodynamic influence from the gap between twin caissons by a scaled boundary finite element method［J］.The Ocean Engineering，2006(2):29-37.

［7］SUN Liang，TAYLOR P.First-and second-order analysis of resonant waves between adjacent barges［J］.Journal of Fluids and Structures，2010，26:954-978.

［8］TAYLOR E，SUN Liang，TAYLOR P.Gap resonances in focused wave groups［C］//23th Int Workshop on Water Waves and Floating Bodies.Jeju，2008:13-16.

［9］SAITHO T，MIAO Guoping，ISHIDA H.Theoretical analysis on appearance condition of fluid resonance in a narrow gap between modules of very large floating structure［C］//Proc 3rd Asia-Pacific Workshop on Marine Hydrodynamics.Shanghai，2006:805-817.

［10］LU Lin，CHENG Liang，TENG Bin，et al.Comparison of potential f l ow and viscous f l uid models in gap resonance［C］//25th Int Workshop on Water Waves and Floating Bodies.Harbin，2010:1-4.

［11］LU Lin，TENG Bin，CHENG Liang，et al.Modelling of multi-bodies in close proximity under water waves-Fluid resonance in narrow gaps［J］.Science China Physics，Mechanics＆ Astronomy，2011，54(3):16-25.

［12］LU Lin，CHEN Xiaobo.Dissipation in the gap resonance between two bodies［C］//27th Int Workshop on Water Waves and Floating Bodies.Copenhagen，2012:22-25.

［13］KRISTIANSEN T，FALTINSEN O M.Gap resonance analyzed by a new domain-decomposition method combining potential and viscous f l ow DRAFT［J］.Applied Ocean Research，2012，34:198-208.

［14］KRISTIANSEN T，FALTINSEN O M.Application of a vortex tracking method to the piston-like behaviour in a semientrained vertical gap ［J］.Applied Ocean Research，2008，30:1-16.

［15］FREDRIKSEN A G，KRISTIANSEN T，FALTINSEN O M.Experimental and numerical investigation of wave resonance in moonpools at low forward speed［J］.Applied Ocean Research，2014，47:28-46.

［16］LIU Yong，LI Huajun.A new semi-analytical solution for gap resonance between twin rectangular boxes［J］.Proceedings of the Institution of Mechanical Engineers，Part M:Journal of Engineering for the Maritime Environment，2014，228(1):3-16.

［17］ZHANG Xinshu，BANDYK P.On two-dimensional moonpool resonance for twin bodies in a two-layer f l uid［J］.Applied Ocean Research，2013，40:1-13.