Janus-Helmholtz 水声换能器理论问题研究

桑永杰，蓝宇

(1.哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001;2.哈尔滨工程大学水声工程学院，黑龙江哈尔滨150001)

现代潜艇大量应用减振降噪技术，辐射噪声越来越低，一些安静型潜艇的辐射噪声甚至接近于海洋环境噪声，传统的利用被动声呐探潜的手段受到了很大挑战。当前，世界各海军强国逐渐把声学探潜的重点重新转到主动声呐上，因此具有低频、大功率特性的水声换能器成为国内外学者研究的热点［1-2］。另外，在远程水声通信等水声对抗领域、基于声学手段的海洋环境监测领域以及深海地质勘探领域，对低频大功率水声换能器的工作深度及工作带宽也提出了现实要求［3-4］。常见的水声换能器在实现低频、宽带、大功率、深水等指标方面存在着固有不足，如弯张换能器具有低频、大功率发射的特点，但工作带宽和工作深度不足;Tonpilz换能器能宽带、大功率、深水工作，但低频谐振发射时体积、重量过大;电动式换能器能实现超低频发射，但声源级和效率很低，工作深度也有限。Helmholtz水声换能器利用了液腔振动，具有谐振频率低、发射效率和声源级高、无限工作深度等特点，结合激励源的结构振动模态则可以实现宽带发射。近年来国内外学者基于Helmholtz谐振腔结构设计了多种新型Helmholtz水声换能器，使得Helmholtz水声换能器的性能得到了进一步提升。

1 Janus-Helmholtz换能器的等效电路及工作机理

Janus-Helmholtz换能器是诸多新型 Helmholtz水声换能器中性能较为突出的一种，其结构示意图如图1所示［5］。文献［6］报道了研制的一只工作频段为500～2 000 Hz，声源级约199 dB的试验样机。本文针对Janus-Helmholtz换能器的几个理论问题开展研究，如Janus换能器纵振动谐振频率在水中高于空气中的原因、液腔振动和Janus换能器纵振动耦合形成宽带发射的机理、弹性腔体对液腔振动性能的影响机理等。

图1 Janus-Helmholtz换能器结构示意图Fig.1 Janus-Helmholtz transducer

等效电路法是分析和设计水声换能器的主要方法之一。Janus-Helmholtz换能器由于涉及到Helmholtz谐振腔参与声辐射，因此其等效电路图中存在多个声辐射支路，且这些支路之间并不是相互独立的。依据电-力-声类比，Janus-Helmholtz换能器的等效电路图可表示为图2所示的形式。

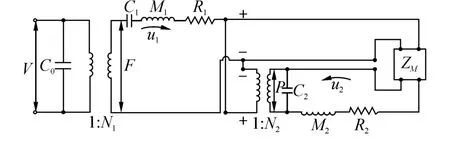
图2 Janus-Helmholtz换能器的等效电路图Fig.2 Equivalent circuit of Janus-Helmholtz transducer

在图2中，V为加载于压电陶瓷材料两端的电压，C0为压电晶堆的静态电容，N1为厚度方向极化的压电陶瓷圆片的机电转换系数，C1为Janus换能器纵向振动时的机械顺性，M1为Janus换能器振动时的动态质量，R1为机械振动阻。流经3个元件的为振速u1。电路图中有2个动态支路，分别代表着Janus换能器纵振动(上支路)和液腔振动(下支路)，振速流经上支路时方向为顺时针，意味着该振动产生的声辐射由辐射盖板的外表面推动，振速流经下支路时方向为逆时针，意味着Helmholtz谐振腔内的流体振动是由辐射盖板的背面推动，即2种振动存在180°的固有相位差(假设声波波长远大于结构尺寸)。N2为机声转换系数，C2为Helmholtz谐振腔的声容，M2为声质量，R2为声阻。Zm为液腔振动产生的声辐射与Janus纵振动产生的声辐射之间相互作用引入的互辐射阻抗。此外，如果腔体的弹性不可忽略，即存在着腔体的声散射，等效电路图中还包含反映腔体散射的第3条支路，如图3示。腔体的弹性与腔体的形状、材质及厚度有关，为了满足刚性壁条件，腔体一般选用杨氏模量大的金属，且需一定的厚度，这样在理论计算液腔谐振频率时才可忽略腔体弹性的影响，即第3条支路断路。

在低频时，图3所示的电路图中第2条和第3条支路可以合并为图4所示的形式，其中Ra和Ma为Helmholtz谐振腔辐射时的声阻及声质量;Ca为Helmholtz谐振腔的声容。腔体自身的等效声阻抗可归结为一个容性元件Cp附加到Helmholtz谐振腔的声容中［7-8］。此时液腔谐振频率公式可以近似写为

由上式可以看出，比起刚性壁条件下的液腔谐振频率表达式，该表达式分母增加了一项Cp，因此液腔谐振频率有所降低。

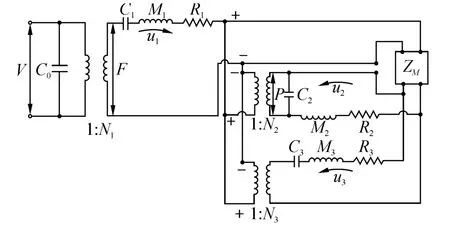
图3 考虑腔体弹性时的机电声等效图Fig.3 Equivalent circuit when elasticity of housing is considered

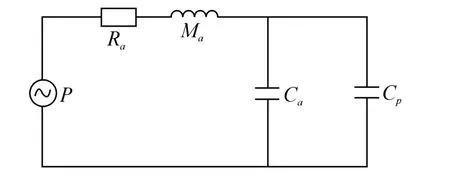
图4 低频时弹性Helmholtz谐振腔等效图Fig.4 Equivalent circuit of elastic Helmholtz resonatorat low frequency

由于存在互辐射阻抗，液腔谐振频率和Janus换能器的纵振动谐振频率与各自在独立状态下的值有所不同，具体高于或低于独立状态下的值，取决于Janus-Helmholtz换能器的长度和波长之比，即d/λ，Janus-Helmholtz换能器工作时类似于由Helmholtz谐振腔和Janus换能器组成了一个二元基阵。基阵基元之间的互辐射阻和互辐射抗随d/λ变化，可正可负。互辐射阻正负影响着基阵的辐射效率，而互辐射抗的正负使得同振质量相对于独立状态下有所增加或减小，因而决定着基元谐振频率的变化情况。以Janus-Helmholtz换能器的纵振动谐振频率为例，独立状态时该谐振频率可表示为［7］

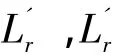
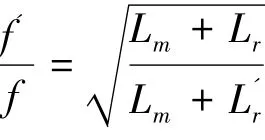
Janus-Helmholtz换能器通常工作在如图1所示的0°方向和90°方向。在90°方向上，换能器不呈现指向性;在0°方向上则呈现一定的指向性。本文主要研究Janus-Helmholtz换能器在0°方向上的发射特性。

Janus-Helmholtz换能器在水中工作时，低频段出现Helmholtz谐振腔产生的液腔谐振，它对Janus换能器低频纵振动产生的声能量进行放大，决定了Janus-Helmholtz换能器的下限工作频率;在高频段有Janus换能器的纵向谐振，决定着Janus-Helmholtz换能器上限工作频率。在声波波长远大于换能器尺寸的假设下，液腔振动和Janus换能器纵向振动在0°方向远场某处产生的声压相位关系为［9］:在液腔谐振频率和Janus换能器纵向谐振频率之间，属于液腔振动的质量控制区及Janus换能器纵向振动的刚度控制区，2种振动产生的声压存在180°相位差，如图5(a)所示，但由于2种振动为辐射盖板的前后面推动，因此存在固有的180°相位差，故综合起来2种振动产生的声压相位差为0°，如图5(b)所示，声压正相叠加，使得该频段内声压频响曲线变得平坦。

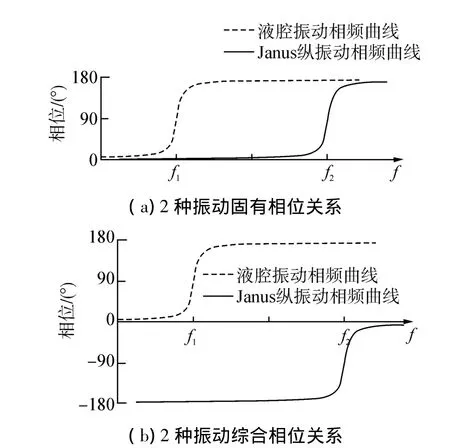
图5 2种振动产生的声压相频曲线图Fig.5 Sound pressure phase frequency curves of the two vibrations

2 Janus-Helmholtz换能器样机有限元优化设计

利用等效电路法分析Janus-Helmholtz换能器往往要基于多种假设与近似，如刚性壁条件、等效集中参数模型、声波波长远大于结构尺寸等，求解过程复杂且精度不足。工程上设计结构复杂的水声换能器时更多地采用有限元法，借助于有限元软件如ANSYS、ATILA等进行换能器结构优化设计，预报换能器的振动和声学性能。

2.1 模态分析

对水声换能器进行模态分析的意义在于可以掌握换能器主振区和节面的位置，以便于合理设置非结构振动附件(如法兰、障板等)，避免附件影响结构振动性能。此外，利用模态分析还可掌握结构振动的谐振频率等信息。

建立的Janus换能器有限元模型和模态分析结果如图6所示。本文设计的虚拟样机Janus换能器纵振动谐振频率在空气中约为2.24 kHz。

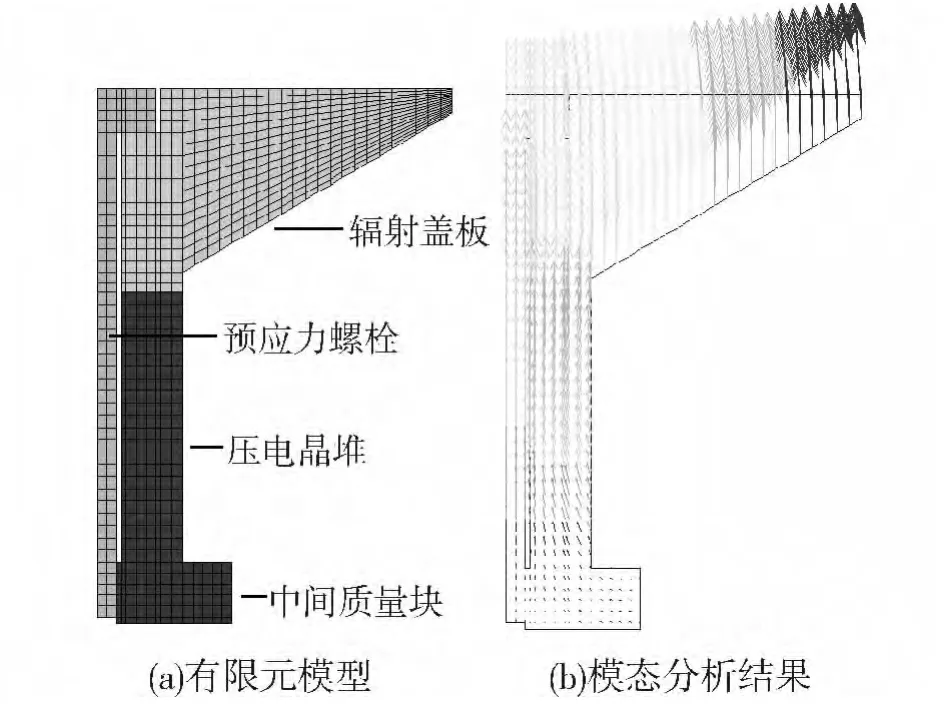
图6 Janus换能器有限元模型和模态分析结果Fig.6 Finite element model and modal analysis results of the Janus transducer

由图6(b)的模态分析结果可以看出，振动位移最大处位于辐射盖板边缘处，因此在引入腔体后该边缘处要保证自由边界条件;振动节面位于中间质量块的中心面处，因此该处可设置连接附件以将腔体和Janus换能器固定在一起。

2.2 水中的谐响应分析

对水声换能器进行水中谐响应分析可以得到电导纳、发送电压响应、声源级等参量的频响曲线，还可以依据求解结果计算出电声效率、机械品质因数、带宽等。建立的Janus-Helmholtz换能器水中有限元模型如图7所示。

通过结构优化设计，最终确定了换能器各结构的尺寸。虚拟样机的发送电压响应曲线如图8所示，水中的电导纳曲线如图9所示。由该图可以看出虚拟样机的液腔谐振频率约为1.14 kHz，Janus换能器纵振动谐振频率约为2.32 kHz，比起空气中的谐振频率2.24 kHz略高，显示出在纵振动谐振频率处互辐射阻抗为负值。

图7 Janus-Helmholtz换能器水中有限元模型Fig.7 Finite element model of the Janus-Helmholtz transducer in water

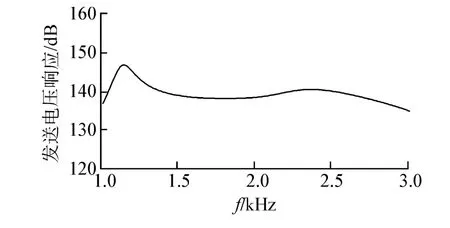
图8 虚拟样机的发送电压响应曲线Fig.8 Transmitting voltage response curve of the virtual prototype

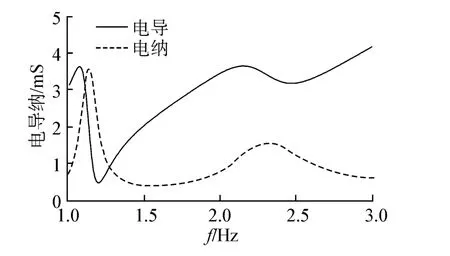
图9 虚拟样机水中的电导纳曲线Fig.9 Admittance curves of the virtual prototype in water

3 换能器试验样机制作与测试

依据有限元优化设计结果，制作了试验样机，如图10。样机的最大直径为0.316 m，最大长度为0.436 m，空气中重约 47 kg。

在哈尔滨工程大学水声技术重点实验室的消声水池测试了该样机的电声性能。该消声水池的消声下限频率为1 kHz，满足该试验样机的测试需求。图11为空气中测得的样机的电导纳曲线，Janus换能器的纵振动谐振频率为2.27 kHz。图12为在水池中测量的电导纳曲线，液腔谐振频率约为1.16 kHz，Janus换能器纵振动谐振频率约为2.39 kHz，该纵振动谐振频率高于空气中的纵振动谐振频率，与理论预测趋势相符。图13、14是发送电压响应及声源级测试结果，其中测试声源级时加载在压电陶瓷片上的电压为3 000 V(峰峰值)。

图10 Janus-Helmholtz换能器样机照片Fig.10 The Janus-Helmholtz transducer prototype

图11 测试的空气中电导纳曲线Fig.11 Measured admittance curves of the prototype in air

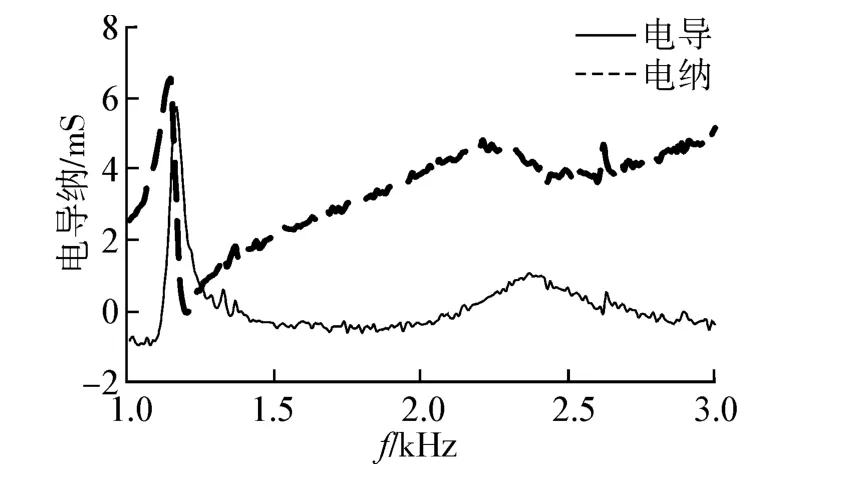
图12 测试的水中电导纳曲线Fig.12 Measured admittance curves of the prototype in water

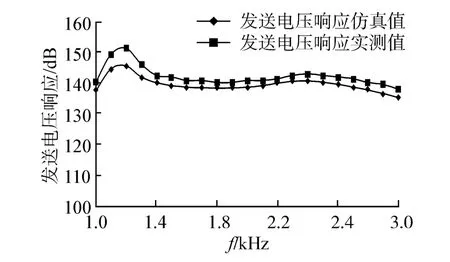
图13 试验样机发送电压响应测试曲线Fig.13 Measured transmitting voltage response curves of the prototype

图14 试验样机声源级测试曲线Fig.14 Measured source level curve of the prototype

由图13可以看出，实测值与仿真值趋势基本一致。由图14可以看出，在1～3 kHz频率范围内，该样机的声源级大于200 dB，最大声源级约为204 dB。在液腔谐振频率处并未表现出与发送电压响应相适应的声辐射能力，主要原因在于大功率驱动时该处由于出现液腔谐振，腔体内的愈量压强很高，容易出现空化现象，造成声辐射能力下降。若在深海环境下工作，则有望抑制空化现象。

4 结论

给出了基于互辐射理论的Janus-Helmholtz换能器等效电路图，研究了Janus-Helmholtz换能器的几个理论问题，得出的主要结论如下:

1)液腔振动和Janus纵振动产生的声辐射存在互辐射作用，互辐射抗在纵振动谐振频率处为负值是纵振动谐振频率在水中高于空气中的原因;

2)在2个谐振频率之间的频段，两种振动产生的声压经2个180°反相后，在0°方向正相叠加使得该频段内声压频响曲线变得平坦;

3)低频时腔体的弹性不能忽略，腔体弹性可归结为与一个与腔体声容并联的容性元件添加到腔体的声容中，增大了腔体的顺性使得液腔谐振频率较刚性壁时有所降低。

［1］周利生，胡青.水声发射换能器技术研究综述［J］.哈尔滨工程大学学报，2010，31(7):932-937.

ZHOU Lisheng，HU Qing.Summarization of underwater acoustic projector technologies［J］.Journal of Harbin Engineering University，2010，31(7):932-937.

［2］解宝兴，郝拥军，程玲.水下远程探测的研究和发展方向［J］.舰船科学技术，2008，30(3):17-21.

XIE Baoxing，HAO Yongjun，CHENG Ling.Underwater remote detection research and development［J］.Ship Science and Technology，2008，30(3):17-21.

［3］MARSSET T，MARSSET B，KER S.High and very high resolution deep-towed seismic system:Performance and examples from deep water Geohazard studies［J］.Deep Sea Research Part I:Oceanographic Research Papers，2010，57(4):628-637.

［4］SATHISHKUMAR R.2 kHz high power smart transducer for acoustic sub-bottom profiling applications［J］.Journal of Marine Science and Application，2013，12(3):361-365.

［5］LE Y，GALL B D.300Hz Janus-Helmholtz transducer for ocean acoustic tomography ［C］//Proc Conf Oceans 93，IEEE.Piscataway，USA，1993:1278-1281.

［6］桑永杰，蓝宇.低频大功率Janus-Helmholtz换能器的设计［J］.陕西师范大学学报:自然科学版，2013，41(6):21-26.

SANG Yongjie，LAN Yu.Design of low-frequency high-power Janus-Helmholtz underwater acoustic transducer［J］.Journal of Shaanxi Normal University:Natural Science Edition，2013，41(6):21-26.

［7］王泽锋，胡永明，熊水东.腔壁弹性对水下小型圆柱形亥姆霍兹共振器共振频率的影响［J］.物理学报，2009，58(4):2507-2512.

WANG Zefeng，HU Yongming，XIONG Shuidong.Influence of cavity wall elasticity on re sonant frequency of small underwater cylindrical Helmholtz resonator［J］.Chin Phys Soc，2009，58(4):2507-2512.

［8］王泽锋，胡永明，孟洲.水下圆柱形Helmholtz共振器的声学特性分析［J］.物理学报，2008，51(11):7022-7028.

WANG Zefeng，HU Yongming，MENG Zhou.Acoustic characteristics of underwater cylindrical Helmholtz resonator［J］.Chin Phys Soc，2008，51(11):7022-7028.

［9］桑永杰，蓝宇.多液腔 Janus-Helmholtz水声换能器［J］.哈尔滨工程大学学报，2013，34(10):1261-1266.

SANG Yongjie，LAN Yu.Multicavity Janus-Helmholtz underwater acoustic transducer［J］.Journal of Harbin Engineering University，2013，34(10):1261-1266.

［10］傅临泰.互辐射影响与基阵设计［J］.声学与电子工程，1990(18):2-12.

FU Lintai.Mutual radiation effects and design of array ［J］Acoustics and Electronics Engineering，1990(18):2-12.

［11］莫喜平.ANSYS软件在模拟分析声学换能器中的应用［J］.声学技术，2007，26(6):1280-1290.

MO Xiping.Simulation and analysis of acoustics transducers using the ANSYS software［J］.Technical Acoustics，2007，26(6):1280-1290.