基于样本累积响应面法的防波堤可靠度分析

刘君，魏开涛，易平

(1.大连理工大学海岸与近海工程国家重点实验室，辽宁大连116024;2.大连理工大学建设工程学部，辽宁大连116024)

核电工程中的防波堤是核电海工构筑物非安全级类物项的重要一项，其稳定性对厂区及取排水设施的正常运行有很大影响［1］。由于防波堤地基土以及筑堤材料强度变异性较大，仅仅用安全系数评价防波堤结构的稳定性是不够的，需要进行可靠度分析作为补充［2-3］。在防波堤这类岩土工程可靠度分析中，功能函数不能显式表达，只能通过有限元强度折减法、Bishop条分法等数值方法得到离散值［4-5］。此时，虽然能用蒙特卡罗法进行可靠度分析，但工作量非常大，另一常用的方法是响应面法(response surface method，RSM)［6-8］。响应面方法通过确定性的计算生成一系列样本点，然后利用这些样本点来拟合一个响应面，并以此代替真实的极限状态曲面进行可靠性分析。不少学者在精度、收敛性和计算效率上对响应面法做了改善［9-14］，但当前应用较多的仍是Bucher的响应面法及其局部改进［15］。这类响应面法采用不含交叉项的二次多项式，通过抽样点信息确定多项式系数，得到近似显式功能函数，基于此进行可靠性分析计算验算点和可靠指标;初次生成的响应面通常不能很好地拟合原功能函数，需要多次迭代生成多个响应面，每次都需重新取样进行有限元分析，工作量偏大［16-18］。有学者已经意识到将之前计算得到的样本点信息摈弃是对资源的极大浪费，提出了一些基于样本重复使用来构造功能函数的结构可靠度计算方法［19-20］。

本文采用拉丁超立方抽样技术取样，在响应面构造时，将历史样本点全部累积或有选择性累积到新生成样本点中，利用累积的样本点构造响应面函数计算可靠指标，循环迭代，直至收敛。通过算例验证了样本累积法使样本点得到了最大程度的利用，迭代也更容易收敛，提高了计算效率;最后对某核电工程防波堤进行了稳定可靠性分析。

1 基本原理

1.1 拉丁超立方抽样

构造响应面的第一步就是进行抽样，样本点的选择直接影响着响应面的好坏和可靠指标的计算效率。为了有效改进抽样效率，从而能够用较少的抽样次数得到较理想的结果，本文采用拉丁超立方抽样(Latin hypercube sampling，LHS)［21］技术进行抽样，该方法被认为是目前最有效的实验设计方法之一［22-23］。

该方法先确定样本数m，对于随机变量xi(i=1，2，…，n)，将每个变量的取值范围平均分成m个互不重叠的子区间。每次抽样仅抽取变量xi某一子区间中的一个随机数，每个变量均进行如此抽样，从而得到第j个样本点xj=(xj1，xj2…，xjn)(j=1，2，…，m)。每个子区间只抽样一次，最终得到m组样本。

1.2 样本累积响应面法的计算步骤

在工程实践中，很多情况下难以得到极限状态函数的明确表达式，这时候可以采用响应面法来近似拟合实际的极限状态函数。响应面法就是通过一系列确定性“试验”生成一系列样本点，然后利用这些样本点来拟合一个响应面，并以此代替真实的极限状态曲面，从而进行可靠性分析。

一般可以取不含交叉项的二次多项式形式:

式中:a=［a0，ai，aii］T是待定系数，n 是随机变量的个数，xi为随机变量。

待定系数a的个数k根据响应面函数的形式确定。对于不含交叉项的二次多项式，待定系数个数k=2n+1，因此需要进行m(m≥k)次独立试验，得到m个样本点及其对应的响应值g(xj)(j=1，…，m)。由于方程组条件数不好，通常都是病态的，因此本文求解响应面待定系数时采用最小二乘QR分解算法(least squares QR，LSQR)［24］，该方法对于求解病态方程组有较好的效果。

对于边坡稳定问题，随机变量一般包括黏聚力、内摩擦角、重度和孔隙水压力等参数;极限状态函数一般取为 g(x1，x2，…，xn)=Fs-1=0，Fs为边坡稳定安全系数，本文采用强度折减法通过FLAC3D软件来计算安全系数。如果记μi和σi分别为随机变量的均值和标准差，Li和Ui分别为随机变量的下限和上限，基于LHS技术的样本累积法边坡稳定可靠度分析的步骤如下:

1)采用LHS方法在μi±3σi内抽取2n+1组样本，并保证样本在该随机变量许可的上下限内，计算对应的安全系数及功能函数值;

2)采用最小二乘QR分解算法计算待定系数a，然后得到响应面，进而采用Matlab优化函数fmincon计算对应的可靠指标βi及验算点xi*。3)如果|βi-βi-1|≤ ε，则迭代收敛，βi和 xi*即为最终的可靠指标β*及验算点x*。否则以新验算点xi

*为中心点，在［xi*-σi，xi*+σi］范围内采用LHS方法抽取2n+1组新样本，并与前面所有样本累积共同来确定新的响应面。由于前面的样本已经是确定的了，仅是新增的2n+1组样本需要计算安全系数，这个计算量与传统响应面法的计算量是相同的。由于样本累积法最大限度地利用了已生成的样本点信息，可以防止迭代陷入局部极值，从而减少迭代次数，提高计算效率。

4)重复步骤 2、3，直至|βi-βi-1|≤ε。

2 算例验证

2.1 算例1

如果把传统不采用样本累积的方法记为方法1(不累积)，而把采用样本累积的方法称为方法2(全部累积)，采用不含交叉项的二次多项式来拟合响应面，2种方法得到的可靠指标计算结果列于表1，迭代过程如图1所示。从表1和图1中可以看出，采用样本累积的方法2用较少的迭代次数得到了收敛解，误差不到2%;而没有采用样本累积的方法1不仅迭代次数多，而且没能得到收敛解。

表1 算例1计算结果对比Table 1 Results comparison of example 1

图1 算例1的迭代过程Fig.1 Iteration process of example 1

2.2 算例 2

图2是两层边坡的剖面图［26］，表2给出了随机变量的分布类型和参数取值，重度 γ=19 kN/m3。模型共有1 200个单元和2 560个节点，采用摩尔-库伦强度准则，这里取△β≤0.01作为收敛标准。

图2 两层边坡剖面Fig.2 Cross-section of a two-layered slope

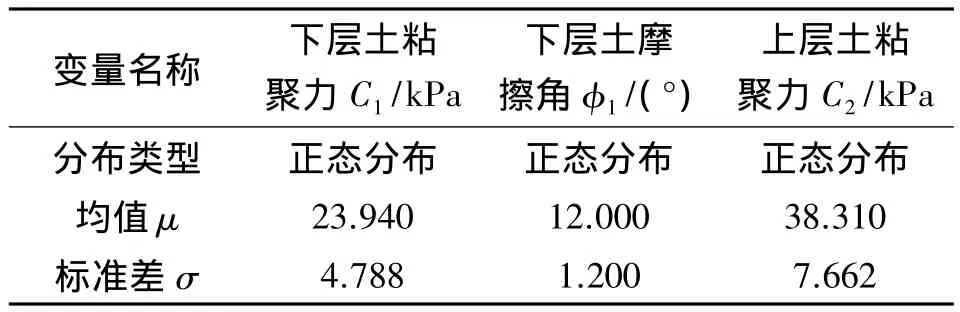
表2 变量及其参数值Table 2 Variables and parameter values

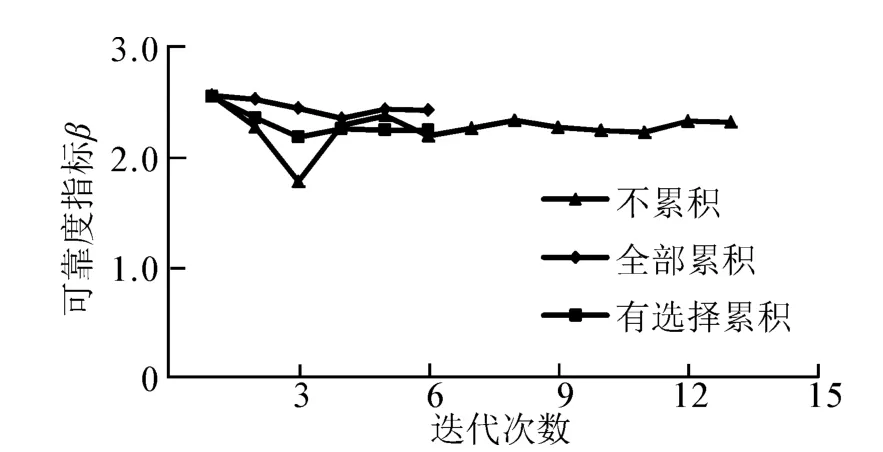
图3 算例2的迭代过程Fig.3 Iteration process of example 2

表3 可靠度分析结果Table 3 Reliability analysis results

当随机变量取均值时，边坡的安全系数Fs(μ)=1.650，这与 Xu 等［27］计算的 Fs(μ)=1.646(有限元法)和 1.634(Spencer非圆弧滑面法)是吻合的，表明边坡稳定安全系数的计算过程是准确可靠的。图3给出了不累积和全部累积2种方法的可靠指标迭代收敛过程，表3给出了2种响应面构造方法的可靠指标计算结果。结果表明，采用方法2仅进行6次迭代即可得到收敛结果，而采用方法1需要13次迭代。虽然方法2得到的可靠指标稍微偏大，但与方法1的结果也仅相差不到5%，效率却提高了1倍。将随机变量的均值μ代入上述2种方法构造的响应面中，安全系数分别为 Fs1(μ)=1.75，Fs2(μ)=1.69，与 Fs(μ)=1.65 的误差分 别 是 6.1% 和2.4%。验算点处的功能函数 g(x*)分别为0.02和0.04，与g(x*)=0相比误差很小。这些计算结果表明方法2构造的响应面能很好地拟合极限状态函数，并有较高的计算效率。

如果在进行样本累积时有所选择，仅将靠近极限状态曲面的样本点累积并参与响应面的构造，而摈弃远离极限状态曲面的样本点，这样可以避免不好样本的干扰，又可以充分利用已有的样本点信息，从而提高收敛效率和可靠度计算精度。

图3给出了有选择样本累积方法(选择标准为与极限状态曲面距离小于0.1范围内的样本点)的可靠度迭代收敛过程，虽然与全部累积方法的迭代次数相同，但可靠性指标要精确一些。表3也给出了有选择累积法得到的验算点和可靠性指标值。

3 核电防波堤可靠性分析

某核电厂海域工程的一典型防波堤断面如图4所示。水位为最高天文潮+100年一遇增水位，距离堤顶3.09 m。材料参数根据工程勘察报告取值［28］，见表4和表5。假设9个随机变量均符合正态分布，每次迭代需抽取19个样本点。

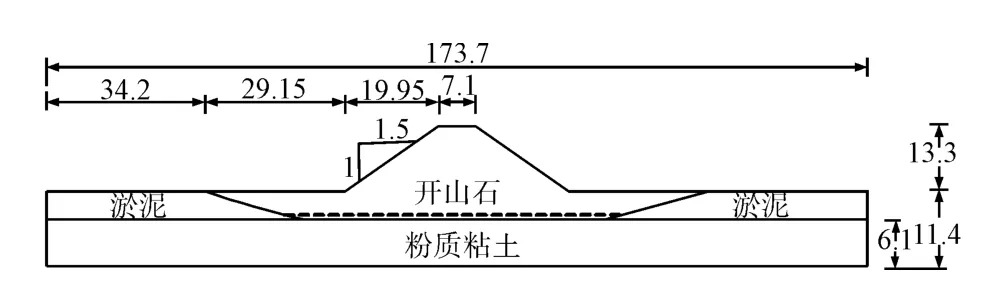
图4 防波堤断面Fig.4 Cross-section of a breakwater

表4 材料参数Table 4 Material parameters

表5 强度参数变异性表Table 5 Variability of strength parameter

核电厂防波堤要根据极限安全地震动确定其稳定性计算的地震作用。在设计基准期内，年超越概率为 0.1‰的地震动峰值加速度不小于0.15 g［1］。考虑静力(工况1)和动力(工况2)2种工况，计算模型共有1 826个单元，3 968个节点。水平向加速度代表值为 0.15 g，竖直向为 0.10 g，顶部加速度放大倍数为2.5。由于工程实际中多采用爆炸挤淤法填筑堤身，假设开山石下有0.5 m厚未挤淤干净的淤泥层，如图4虚线所示。含淤泥层的静力和动力工况分别记为工况3和工况4。

表6给出了4个工况下随机变量取不同值时的安全系数。对于静力情况的工况1和工况3，当土体参数取为最不利的情况时安全系数分别为1.270和1.066，表明这2种工况的失效概率为0，即在静力条件下，不管开山石下部有没有0.5 m厚淤泥夹层，防波堤都是安全的。

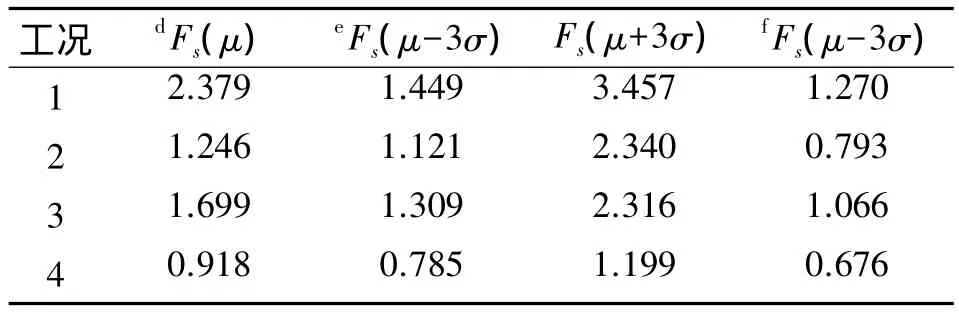
表6 各工况的安全系数Table 6 The safety factors for each case

从表6可以看出，对于工况2，当强度参数C和φ取均值减3倍标准差而重度γ'取均值加3倍标准差时，安全系数为0.793，表明结构有失稳的可能。对于工况4，在表6所列的4种情况下，有3种情况的边坡安全系数均小于1.0，说明结构失稳的可能性较大。采用样本累积法计算了工况2和4这2个工况的可靠指标和失效概率。

在采用样本累积法构造响应面时考虑了2种处理手段:1)所有已有样本全部参与响应面的构造，与前面2个算例相同;2)仅选择离极限状态曲面很近的样本点参与累积和响应面的构造，那些远离极限状态曲面的样本点不参与。图5给出了工况4中2种累积方法收敛性的比较。从图中可以看出，有选择的样本累积法(选择标准为与极限状态曲面距离小于0.1范围内的样本点)可以更快速的收敛，而且没有震荡的现象。图6给出了工况2的收敛过程，参与累积的样本选择标准为与极限状态曲面距离小于0.3范围内的样本点。表7给出了2种工况分别在有选择情况下样本累积法的迭代次数及最终的可靠指标和失效概率。

图5 工况4的迭代过程Fig.5 Iteration process of case 4

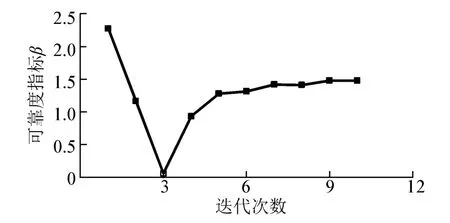
图6 工况2的迭代过程Fig.6 Iteration process of case 2

表7 工况2和工况4的可靠度分析结果Table 7 Reliability analysis of cases 2 and 4

上述计算表明，虽然当变量取均值时的安全系数大于1，但有时失效概率还很高，可靠度分析作为安全系数法评价的补充是非常必要的。地震荷载作用下，防波堤有一定的失效概率;当开山石堤身底部有淤泥夹层，结构的失效概率会变得很大，这种情况对核电工程的正常运行是非常不利的，值得工程人员重视。

4 结论

本文基于拉丁超立方抽样技术，采用样本累积构造响应面，使样本点得到了最大程度的利用，迭代也更容易收敛，提高了计算效率。通过算例和实际应用可以得到以下结论:

1)岩土工程中含有各种不确定性，在工程设计和决策中用可靠度方法来分析这些不确定因素对结构功能的影响是必要的。

2)通常的响应面构造是在验算点附近取点，如果验算点预测有偏差，可靠度迭代将得不到收敛解，这也表明样本点全局逼近能力差。本文采用累积样本点构造响应面，最大程度地使用了样本点信息，在一定程度上使得构造的响应面函数更为接近真实的功能函数。同时每次迭代都是在原有样本点的基础上增加新的样本点，避免了验算点往复震荡难以收敛，提高了计算效率。

3)当采用样本累积法时，如果对已有样本进行有选择性的累积，可以进一步降低迭代次数，提高计算效率。选择标准取为与极限状态曲面距离小于0.1～0.3范围内的样本点(满足样本点数前提下)。

4)核电工程中防波堤的稳定性对厂区及取排水设施的正常运行有很大影响。计算结果表明仅采用安全系数作为防波堤结构稳定与否的判别是不够的，可靠度分析作为安全系数评价的补充能够为核电工程海工构造物的稳定性判别提供有益的参考。

5)当采用爆炸挤淤法进行防波堤施工时，清淤是否干净将对防波堤的稳定性影响很大，值得工程设计和施工人员高度重视。

［1］国家能源局.NB/T 25002-2011，核电厂海工构筑物设计规范［S］.北京:中国电力出版社，2011.

National Energy Board.NB/T 25002-2011，Code for design of maritime structures of nuclear power plants［S］.Beijing:China Electric Power Press，2011.

［2］US National Research Council.Probabilistic methods in geotechnical engineering，committee on reliability methods for risk mitigation in geotechnical engineering，geotechnical board and board on energy and environmental systems commission on engineering and technical systems［R］.Washington D C:The National Academies，1995.

［3］赵国藩，金伟良，贡金鑫.结构可靠度理论［M］.北京:中国建筑工业出版社，2000:2-10.

ZHAO Guofan，JIN Weiliang，GONG Jinxin.Structural reliability theory［M］.Beijing:China Building Industry Press，2000:2-10.

［4］李典庆，周创兵，陈益峰，等.边坡可靠度分析的随机响应面法及程序实现［J］.岩石力学与工程学报，2010，29(8):1513-1523.

LI Dianqing，ZHOU Chuangbing，CHEN Yifeng，et al.Reliability analysis of slope using stochastic response surface method and code implementation［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(8):1513-1523.

［5］彭振斌，李俊，彭文祥.基于Bishop条分法的边坡可靠度应用研究［J］.中南大学学报:自然科学版，2010，41(2):668-672.

PENG Zhenbin，LI Jun，PENG Wenxiang.Application analysis of slope reliability based on Bishop analytical method［J］.Journal of Central South University:Science and Technology，2010，41(2):668-672.

［6］丁幼亮，李爱群，邓扬，等.响应面法在结构可靠度分析中的应用研究［J］.特种结构，2011(2):12-16.

DING Youliang，LI Aiqun，DENG Yang，et al.Application research of response surface method in structural reliability analysis［J］.Special Structures，2011(2):12-16.

［7］LYU Q，LOW B K.Probabilistic analysis of underground rock excavations using response surface method and SORM［J］.Computers and Geotechnics，2011，38(8):1008-1021.

［8］桂劲松，康海贵.结构可靠度分析的响应面法及其Matlab实现［J］.计算力学学报，2004，21(6):683-687.

GUI Jinsong，KANG Haigui.Response surface method for structural reliability analysis and its realization with Matlab［J］.Chinese Journal of Computational Mechanics，2004，21(6):683-687.

［9］谭晓慧，王建国，刘新荣.改进的响应面法及其在可靠度分析中的应用［J］.岩石力学与工程学报，2005，24(S2):5874-5879.

TAN Xiaohui，WANG Jianguo，LIU Xinrong.Improved response surface method and its application to reliability analysis［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(S2):5874-5879.

［10］王宇，王春磊，汪灿，等.边坡可靠性评价的向量投影响应面研究及应用［J］.岩土工程学报，2011，33(9):1434-1439.

WANG Yu，WANG Chunlei，WANG Can，et al.Reliability evaluation of slopes based on vector projection response surface and its application［J］.Chinese Journal of Geotechnical Engineering，2011，33(9):1434-1439.

［11］李生勇，张哲，石磊，等.一种在响应面法中选取样本点的新方法［J］.计算力学学报，2008，24(6):899-903.

LI Shengyong，ZHANG Zhe，SHI Lei，et al.An new method for selecting sampling points in response surface method［J］.Chinese Journal of Computational Mechanics，2008，24(6):899-903.

［12］谭海涛，徐定海，王善.一种计算结构可靠度的一元分解法［J］.哈尔滨工程大学学报，2009，30(8):883-886.

TAN Haitao，XU Dinghai，WANG Shan.One-dimensional decomposition method for calculation of structural reliability［J］.Journal of Harbin Engineering University，2009，30(8):883-886.

［13］谭晓慧，胡晓军，储诚富，等.模糊响应面法及其在边坡稳定可靠度分析中的应用［J］.中国科学技术大学学报，2011，41(3):233-237.

TAN Xiaohui，HU Xiaojun，CHU Chengfu，et al.Fuzzy response surface method and its application in the reliability analysis of slope stability［J］.Journal of University of Science and Technology of China，2011，41(3):233-237.

［14］LAURENCEAU J，SAGAUT P.Building efficient response surfaces of aerodynamic functions with kriging and cokriging［J］.AIAA Journal，2008，46(2):498-507.

［15］BUCHER C G，BOURGUND U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7(1):57-66.

［16］ZHAO W，QIU Z.An efficient response surface method and its application to structural reliability and reliability-based optimization［J］.Finite Elements in Analysis and Design，2013，67:34-42.

［17］苏永华，赵明华，刘晓明.用遗传算法搜索验算点的复杂响应面函数可靠度分析方法［J］.岩石力学与工程学报，2005，24(S2):5868-5873.

SU Yonghua，ZHAO Minghua，LIU Xiaoming.Reliability degree analysis method of complicated response surface function to search checking point with genetic algorithm method［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(S2):5868-5873.

［18］赵维涛，安伟光，严心池.二阶二次矩可靠性指标［J］.哈尔滨工程大学学报，2004，25(2):240-242.

ZHAO Weitao，AN Weiguang，YAN Xinchi.Second-order second-moment reliability index［J］.Journal of Harbin Engineering University，2004，25(2):240-242.

［19］DAS P K，ZHENG Y.Cumulative formation of response surface and its use in reliability analysis［J］.Probabilistic Engineering Mechanics，2000，15(4):309-315.

［20］冯欢欢，蒋向华.样本重复使用失效响应曲线分析结构可靠度方法［J］.航空动力学报，2013，28(10):2228-2234.

FENG Huanhuan，JIANG Xianghua.Sample points reused failure response curve method for structural reliability analysis［J］.Journal of Aerospace Power，2013，28(10):2228-2234.

［21］MCKAY M D，CONOVER W J，BECKMAN R J.A comparison of three methods for selecting values of input variables in the analysis of output from a computer code［J］.Technometrics，1979，21(2):239-245.

［22］吴振君，王水林，葛修润.LHS方法在边坡可靠度分析中的应用［J］.岩土力学，2010，31(4):1047-1054.

WU Zhenjun，WANG Shuilin，GE Xiurun.Application of Latin hypercube sampling technique to slope reliability analysis［J］.Rock and Soil Mechanics，2010，31(4):1047-1054.

［23］隋允康，宇慧平.响应面方法的改进及其对工程优化的应用［M］.北京:科学出版社，2011:10-11.

SUI Yunkang，YU Huiping.The improvement of the response surface method and its applications to the engineering optimization［M］.Beijing:Science Press，2011:10-11.

［24］PAIGE C C，SAUNDERS M A.LSQR:An algorithm for sparse linear equations and sparse least squares［J］.ACM Transactions on Mathematical Software，1982，8(1):43-71.

［25］LUO Xianfeng，LI Xin，ZHOU Jing，et al.A Krigingbased hybrid optimization algorithm for slope reliability analysis［J］.Structural Safety，2012，34:401-406.

［26］HASSAN A M，WOLFF T F.Search algorithm for minimum reliability index of earth slopes［J］.Journal of Geotechnical and Geoenvironmental Engineering，1999，125(4):301-308.

［27］XU B，LOW B K.Probabilistic stability analyses of embankments based on finite element method［J］.Journal of Geotechnical and Geoenvironmental Engineering，2006，132(11):1444-1454.

［28］核工业南京工程勘察院.辽宁徐大堡核电厂海工工程岩土工程详勘报告，工程编号:2012013［R］.南京:核工业南京工程勘察院，2012.

Nanjing Nuclear Industry Engineering Investigation Institute.Report of the geotechnical engineering for the marine engineering of the Xudabao nuclear power plant in Liaoning，No.2012013［R］.Nanjing:Nanjing Nuclear Industry Engineering Investigation Institute，2012.