水下气动发射装置发射性能参数灵敏度分析

牛清勇，李天匀，朱翔，朱显明

(1.华中科技大学船舶与海洋工程学院，湖北武汉430074;2.华中科技大学船舶和海洋水动力湖北省重点实验室，湖北 武汉430074;3.中国舰船研究设计中心船舶振动噪声重点实验室，湖北武汉430064)

作为一种重要的水声对抗器材，某型水下气动发射装置，利用高压气瓶、发射阀和发射管等组件将武器以一定速度发射出管。建立描述该装置发射过程的数学模型并对内弹道性能进行参数影响规律和灵敏度分析，对该发射系统的优化设计和发射试验的参数估计等均有重要意义。由于保密原因该型发射装置的可收集资料较少。因其与鱼雷或水雷发射装置在部分构件上原理相似，研究该发射装置时可参考其他发射系统的分析方法。针对鱼雷或水雷的发射系统，已经在内弹道数学建模和内流场仿真分析方面开展有许多研究［1-5］。在建立了内弹道模型的基础上，内弹道性能的参数影响规律的研究也随之开展起来。对涡轮泵式鱼雷发射装置［6-7］、水雷发射装置［8］和液压平衡式鱼雷发射装置［9］内弹道性能的参数影响规律的研究表明，发射气瓶初压、发射时潜艇深度和速度以及发射阀的开启规律等对内弹道性能均有影响。发射管内武器的移动速度、发射管内膛压既随发射气瓶初始压强的增加而增大，又随发射阀开启面积的增大而增大。发射深度和艇速等对内弹道性能也有一定的影响。已有文献在分析模型参数对内弹道性能的影响时，只讨论了参数本身的变化对内弹道性能的影响规律，并未针对不同参数之间的影响程度即灵敏度进行比较。

本文以某型水下气动发射装置为对象，在建立了描述发射过程数学模型的基础上，利用局部灵敏度分析方法对内弹道性能的主要参数进行了影响规律分析，并对不同参数之间的灵敏度进行了比较，确定了武器出管速度和最大膛压的主要影响参数。

1 发射系统数学模型

图1为某型水下气动发射装置的结构简图。发射阀开启后，高压空气被引入发射管，武器被推动并冲破端盖处金属密封片以一定速度出管。利用热力学和动力学知识，可建立描述该发射过程的数学模型。

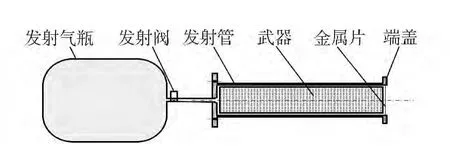
图1 某水下气动发射装置结构简图Fig.1 Sketch of an underwater pneumatic launcher

1.1 发射气瓶模型

由理想气体状态方程和绝热过程状态方程可推出发射气瓶的温度和压强的变化规律:

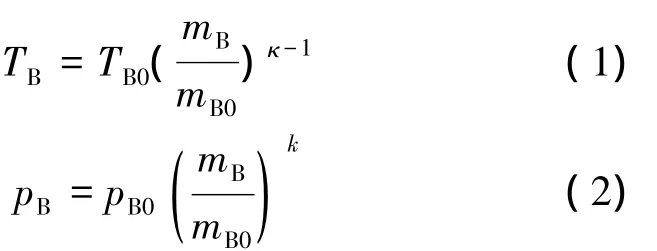
式中:TB0、TB分别为初始时刻(定义为发射阀开启时刻)、发射过程中发射气瓶内空气的温度，K;pB0、pB分别为初始时刻、发射过程中发射气瓶内空气的压强，Pa;mB0、mB分别为初始时刻、发射过程中发射气瓶内空气的质量，mg;κ为绝热指数，κ=1.4。

不计空气泄露，经发射阀流入发射管的空气质量为mi，质量流量为

1.2 发射阀模型

式(3)表示的质量流量又可写成如下形式［10］:

式中:φ为发射阀的流量系数，经验值取0.6～0.65;Ai为发射阀的瞬时开启面积，m2;ρi为发射阀出口截面处的空气密度，kg/m3;ui为发射阀出口截面处的气体流速，m/s。由喷管理论可知，发射阀出口处流速和空气密度分别为

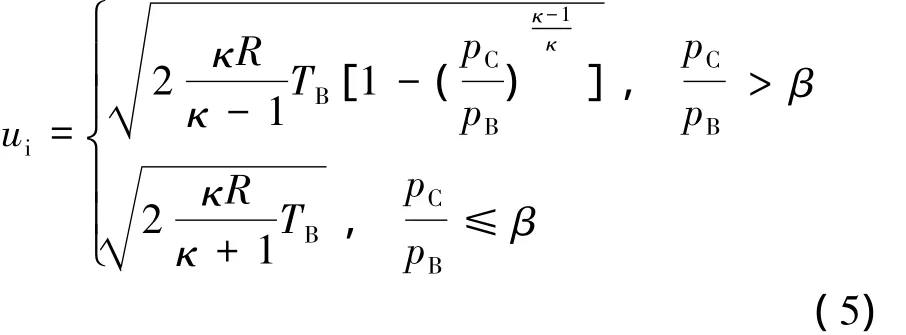
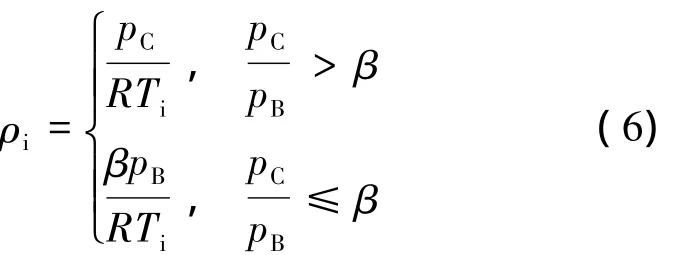
式中:R为理想气体常数，取287 J/(kg·K);pC为发射过程中发射管的内压，Pa;β=［2/(κ +1)］κ/(κ-1)为临界压力比;Ti为发射阀出口截面处的温度:

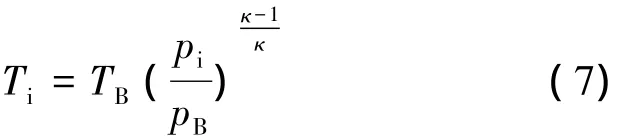
式中:pi为发射阀出口截面处的压强，Pa。

1.3 发射阀开启规律

发射阀的开启规律对于内弹道控制起着重要的作用，其开启面积通常可以表示成随时间变化的连续函数或阶段函数。由于下文中的模型试验中发射阀开启到最大面积后一直保持直至武器出管后才关闭，为便于与试验结果比较，假定发射阀为理想的快开阀模型，其开启面积随时间的变化规律如图2所示。其中t0为发射阀开启动作的响应时间，AV0为最大开启面积。

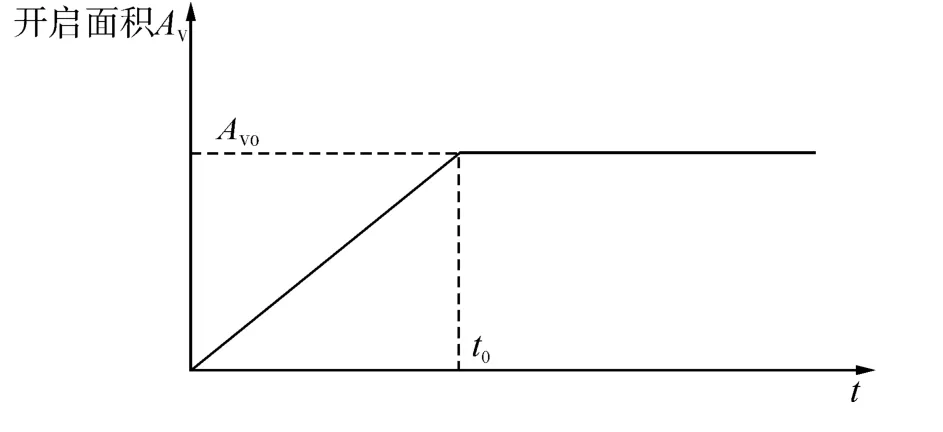
图2 发射阀开启规律Fig.2 Open law of the launch valve

1.4 发射管模型

因武器的保护套管与发射管壁的间隙很小，又由于武器两端的端盖处有密封圈，因此密封片被冲破后外部水没有立即进入发射管且发射管内气体也无溢出。发射前后，发射管内空气体积为连续变化过程，忽略其与管壁间的热交换，发射管内空气的热力学变化过程可用热力学第一定律描述:

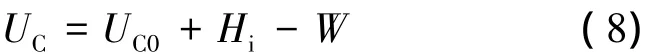
式中:UC、UC0分别为发射过程中和初始时刻发射管内空气的内能，J;Hi为从发射阀流入发射管的空气的热焓，J;W为推动武器运动的力所做的功，J。

发射管内空气的温度TC和压强pC满足:

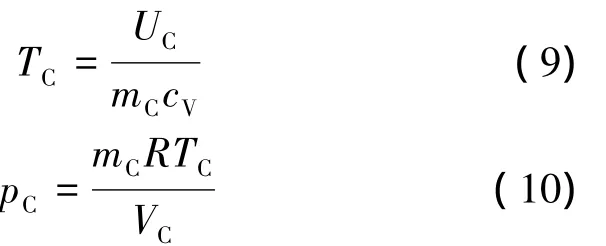
式中:mC为发射管内空气的质量，kg;cV为空气的定容比热，J/(kg·K);VC为发射管内的充气容积，m3。

通过发射阀注入发射管的空气，其热焓注入率为dHi/dt=cpTBdmi/dt。其中，cp为空气的定压比热，J/(kg·K)。考虑到空气经发射阀节流后其滞止温度有所降低，则节流后的空气温度满足经验关系:

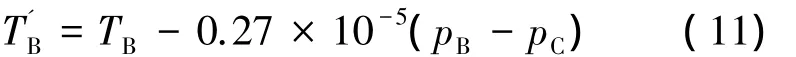
因此，经由发射阀注入发射管的空气热焓注入率为

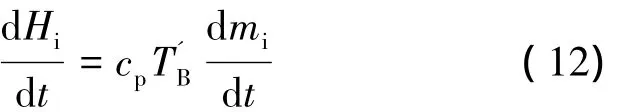
发射管内空气的质量变化率为

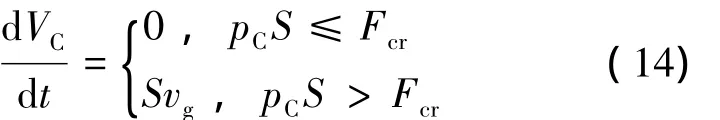
式中:S为武器的横截面面积，m2;vg为武器的运动速度，m/s;Fcr为推动武器开始运动所需克服的初始阻力，主要来源于密封片的冲断阻力。与鱼雷发射装置不同，密封片的存在除了保护管内武器外，还使武器在运动前就已受到较大的推力作用。

1.5 武器在发射管内的运动

武器的运动规律满足:

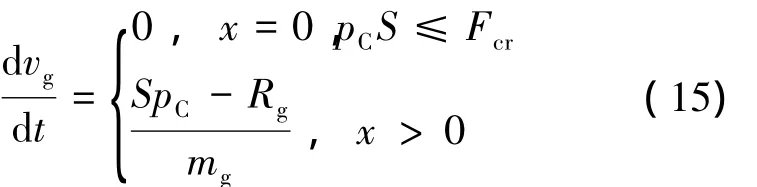
发射开始后，作用于武器底面的推力使武器克服初始阻力开始运动。此过程发射管内充气容积的变化率为

式中:mg为武器质量，kg;x为武器在发射管内的位移;Rg为运动开始后武器所受的阻力，N，可表达为

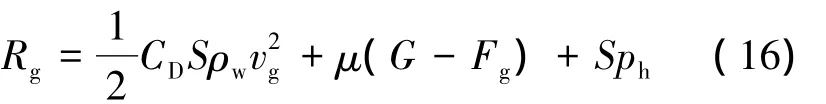
式中:ρw为水的密度，kg/m3;CD为武器水下运动的阻力系数，s2/(m·kg);μ为武器与发射管管壁间的摩擦系数;G为武器的重量，N;Fg为武器所受浮力，N;ph为发射管外的流体压强，Pa。

运动过程中，武器所受推力的做功功率为

利用MATLAB编写程序求解方程(1)～(17)所示的发射系统数学模型，可对发射过程内弹道结果进行仿真分析。

2 模型的有效性验证

利用图3所示的发射试验装置进行了模型发射试验，图4为某次发射过程中武器水下运动的截图。为验证理论模型的有效性，试验中测量了武器在发射管内的运动时间和发射后气瓶气体压强。

模型试验和仿真计算所用参数相同，主要包括:发射气瓶容积0.04 m3，发射管内初始空气体积0.000 5 m3。空气的定压比热 cp为 1 006 J/(kg·K)，定容比热cV为719 J/(kg·K)。武器质量为10 kg，武器发射管内行程为0.8 m，由试验确定的武器运动初始阻力Fcr为9 000 N。发射阀开启动作的响应时间为50 ms，最大开启截面为20 mm2。武器水下运动阻力系数CD取0.8 s2/(m·kg)。

对发射气瓶初始压强为2.50 MPa的发射工况，利用数学模型仿真计算得到的武器管内运动时间为0.138 s，发射后气瓶压强为 2.29 MPa。由水下模型发射试验测到的武器出管时间为0.133 s，发射后气瓶压强为2.25 MPa。数学模型结果与试验结果基本吻合，验证了仿真分析方法的有效性。

图3 发射试验装置Fig.3 Experimental facilities of the launch

图4 发射过程截图Fig.4 Screenshot of the launching process

3 内弹道参数分析

3.1 局部灵敏度分析方法

灵敏度分析用于研究一个系统的状态或输出变化对系统参数变化的敏感程度，其中局部灵敏度分析方法是应用较广泛的一种方法。使用该方法时，一般假定系统 y 是 n 个参数 x1，x2，..，xn的函数。分析某个参数xi的灵敏度时，通常只改变该参数的值，同时保持其余参数不变，由此计算函数值的改变量以衡量参数的影响程度。某个参数xi的局部灵敏度可用如下的偏导数表示［11］:

式中:Si定义为函数在设计点处关于参数xi的灵敏度，的值越大，表示参数xi越灵敏。

对于不同的参数，由式(18)计算得到的结果单位不同，为便于比较，将其无量纲化:

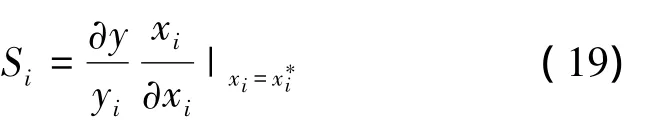
式中:yi是函数在设计点处的函数值。某些系统的解析形式难于得到，为进行局部灵敏度分析，可将参数改变一个微小幅度(如0.5%)采用有限差分法计算灵敏度。

3.2 局部灵敏度结果

水下气动发射系统的内弹道设计目标是在发射膛压允许的条件下使武器以设定的规律出管，因此可取发射过程中最高膛压pC，max和武器的出管速度vg，exit作为内弹道性能的目标函数，分析主要参数武器运动初始阻力Fcr、发射阀最大开启面积AV0、发射气瓶初压pB0和体积VB等的影响规律和灵敏度。以水下试验的参数值为基准，将待分析参数分别减小和增大5%、10%和15%并保持其他参数不变，计算最高膛压和武器出管速度的变化规律及参数灵敏度结果，分别如图5、6所示。

由图5(a)可知，发射管最高膛压与各参数间近似成线性关系。由图5(b)可看出，武器运动初始阻力的灵敏度值最大。随着武器运动初始阻力的增加，发射管最高膛压值也增加。最高膛压与初始阻力这种关系与发射过程内弹道变化有关:当武器冲破密封片开始运动后，发射管内空气体积快速增加引起管内膛压由峰值处迅速下降，因此密封片被冲破瞬时恰好对应着武器克服初始阻力和膛压达到最高值的时刻。

由图6(a)可以看出，武器出管速度与各参数间也近似成线性关系，且随参数的增加而增大。由图6(b)可知，各参数中发射阀最大开启面积和气瓶初压的灵敏度值最大且变化规律接近，武器运动初始阻力的灵敏度值较小，气瓶体积的灵敏度值最小。发射阀最大开启面积和发射气瓶初压，与发射过程中空气推力对武器的做功大小直接相关，因而对武器出管速度的影响最为明显。

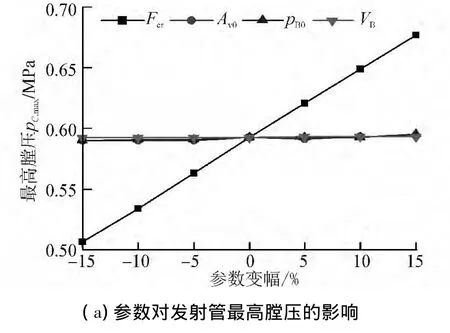
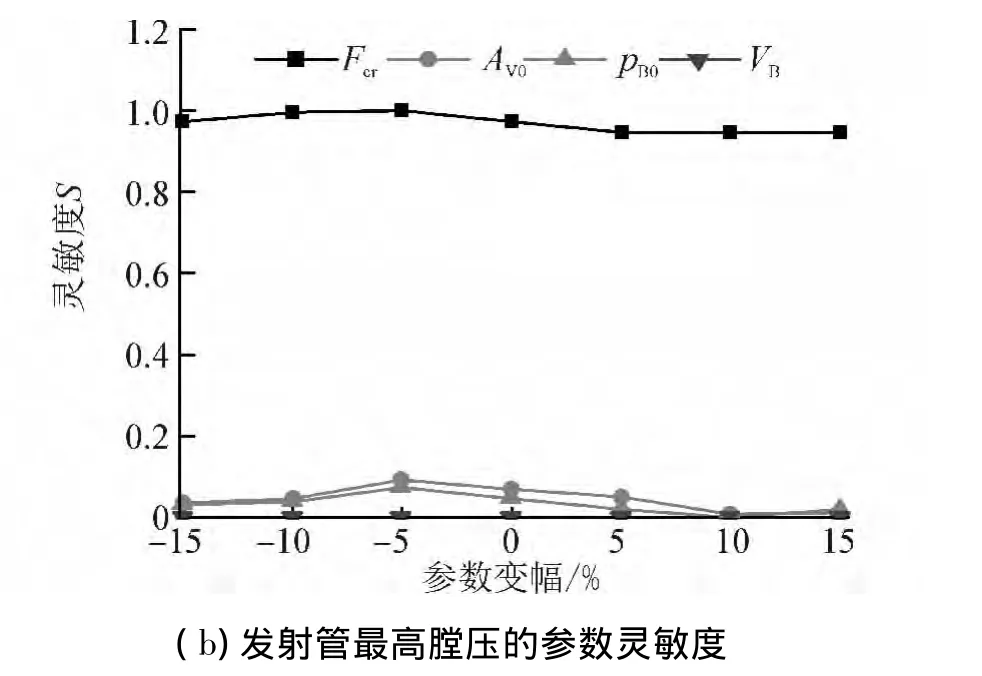
图5 最高膛压的参数影响规律Fig.5 Effect law of parameters on the maximum chamber pressure of the launch tube

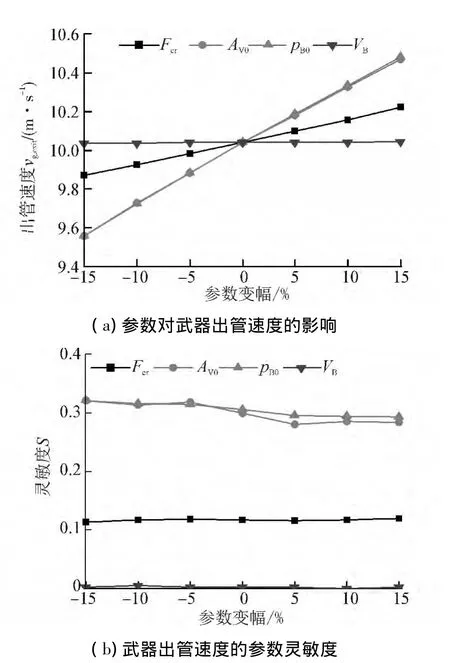
图6 出管速度的参数影响规律Fig.6 Effect law of parameters on the exit velocity of the weapon

通过以上分析可知，为满足发射管最高膛压的允许条件，调整运动初始阻力(主要是调整密封金属片的厚度)效果最显著。为保证武器的出管速度，调整发射气瓶初压和发射阀最大开启面积效果最明显，调整运动初始阻力效果次之。

4 结论

对某型水下气动发射系统进行了内弹道数学建模和参数灵敏度分析。得到如下结论:

1)通过逐个建立发射系统各环节数学模型得到了发射系统的整体模型，发射过程武器管内运动时间和发射气瓶剩余压强的理论和试验结果吻合，验证了该型发射装置内弹道模型的正确性。

2)通过局部灵敏度分析可知:初始阻力对最高膛压的影响最显著，阻力越大最高膛压越大。发射阀最大开启面积、气瓶初压和气瓶体积对最高膛压的影响较小。发射阀最大开启面积和发射气瓶初压对出管速度的影响最明显，出管速度随这2个参数的增加而增加，运动初始阻力对出管速度的影响较小，气瓶体积的影响最小。

3)单参数变化的局部灵敏度分析方法，未能考虑多参数同时变化的影响，更深入的参数影响分析可采用全局灵敏度方法。

4)内弹道性能主要影响参数的确定和影响规律的研究，可为该型发射装置内弹道的优化设计提供参考。

［1］练永庆，王树宗.鱼雷发射装置设计原理［M］.北京:国防工业出版社，2012:169-280.

［2］田兵，王树宗，练永庆.液压蓄能式鱼雷发射装置内弹道建模与仿真［J］.鱼雷技术，2011，19(1):68-71.

TIAN Bing，WANG Shuzong，LIAN Yongqing.Inner trajectory modeling and simulation of hydraulic energy accumulated torpedo launcher［J］.Torpedo Technology，2011，19(1):68-71.

［3］练永庆，田兵，王树宗，等.空气涡轮泵发射系统发射过程仿真分析［J］.兵工学报，2011，32(2):155-162.

LIAN Yongqing，TIAN Bing，WANG Shuzong，et al.Simulation and analysis of the launching process of air-turbine pump launch system［J］.Acta Armamentarii，2011，32(2):155-162.

［4］宋保维，黄海.气动不平衡式鱼雷发射器内弹道流场仿真研究［J］.鱼雷技术，2008，16(2):46-49.

SONG Baowei，HUANG Hai.Simulation of inner trajectory flow field for pneumatic imbalance torpedo launcher［J］.Torpedo Technology，2008，16(2):46-49.

［5］刘乐华，张宇文，袁绪龙.水下大深度垂直发射内流场的数值研究［J］.水动力学研究与进展，2005，20(1):90-94.

LIU Lehua，ZHANG Yuwen，YUAN Xulong.Numerical simulation of the interior flow for launch under deep water［J］.Journal of Hydrodynamics，2005，20(1):90-94.

［6］练永庆，徐勤超，王树宗.空气涡轮机带负载启动过程仿真［J］.机械工程学报，2011，47(8):191-198.

LIAN Yongqing，XU Qinchao，WANG Shuzong.Simulation of startup process of air turbine with load［J］.Journal of Mechanical Engineering，2011，47(8):191-198.

［7］吴朝晖，王树宗，马世杰.旋转泵式鱼雷发射系统建模与仿真［J］.海军工程大学学报，2000，12(5):54-58.

WU Zhaohui，WANG Shuzong，MA Shijie.Building model and simulation of submarine rotary pump torpedo launch system［J］.Journal of Naval University of Engineering，2000，12(5):54-58.

［8］张永，逄洪照，黄波，等.气动不平衡发射装置发射水雷内弹道特性［J］.舰船科学技术，2011，33(12):93-96.

ZHANG Yong，PANG Hongzhao，HUANG Bo，et al.Research on interior trajectory characteristics of the seamine launched by the aerodynamic non-balance torpedo launcher［J］.Ship Science and Technology，2011，33(12):93-96.

［9］陈宜辉，王树宗，练永庆，等.水压平衡式水下发射装置的可调节发射阀研究［J］.机械科学与技术，2006，25(2):210-211.

CHEN Yihui，WANG Shuzong，LIAN Yongqing，et al.Research on the adjustable discharge valve of underwater hydraulic balanced launcher［J］.Mechanical Science and Technology，2006，25(2):210-211.

［10］乔汝椿.涡轮泵式潜艇鱼雷发射装置设计分析［J］.鱼雷技术，2004，12(2):43-46.

QIAO Ruchun.A design analysis of pneumatic turbine pump-type torpedo launcher［J］.Torpedo Technology，2004，12(2):43-46.

［11］束龙仓，王茂枚，刘瑞国，等.地下水数值模拟中的参数灵敏度分析［J］.河海大学学报:自然科学版，2007，35(5):491-495.

SHU Longcang，WANG Maomei，LIU Ruiguo，et al.Sensitivity analysis of parameters in numerical simulation of groundwater［J］.Journal of Hohai University:Natural Sciences，2007，35(5):491-495.