低信噪比突发信号载波频偏估计算法

2015-06-05赵陆文张北江缪志敏李广侠

系统工程与电子技术 2015年12期

关键词：点数门限载波

赵陆文，张北江，缪志敏，李广侠，刘波

（1.解放军理工大学通信工程学院，江苏南京210007；2.解放军理工大学指挥信息系统学院，江苏南京210007）

低信噪比突发信号载波频偏估计算法

赵陆文1，张北江1，缪志敏2，李广侠1，刘波1

（1.解放军理工大学通信工程学院，江苏南京210007；2.解放军理工大学指挥信息系统学院，江苏南京210007）

快速准确的载波频偏估计在突发信号的相干解调中发挥着至关重要的作用。目前的载波频偏估计算法很难同时兼顾估计精度、信噪比（signal-to-noise ratio，SNR）门限以及估计范围等指标。针对这一问题，提出了一种数据辅助的基于接收信号自相关序列离散傅里叶变换（discrete Fourier transform，DFT）的载波频偏估计算法。该算法通过对接收信号的自相关进行加窗处理，借助离散傅里叶变换来实现频率估计。仿真结果表明，与经典的M＆M算法相比，该算法具有更低的信噪比工作门限，在低信噪比情况下具有更低的差错概率和更宽的估计范围，非常适合低信噪比突发信号的载波频偏估计。

载波频偏估计；低信噪比；突发信号；M＆M算法

0 引言

在无线通信中，由于多普勒效应以及收发信机本振不同源，使得接收信号载波与本地载波之间不可避免地存在一定的频差，致使相干解调无法建立，因此对接收信号载波频偏进行估计就显得至关重要。尤其是在突发通信中，为了提高帧效率，需要尽可能压缩导频信号的长度，因此往往需要在极短的时间内完成载波频偏估计。此外，在远距离（比如卫星通信、深空通信）、遮蔽、室内以及干扰条件下，接收到的信号极其微弱［1］。随着高效编码技术的发展，信号的解调门限已越来越低，精确的载波同步技术已成为实现相干解调的一个瓶颈。因此，研究低信噪比（signal-to-noise ratio，SNR）条件下，突发信号载波频偏估计（也称为“频差估计”）就具有非常现实的意义。

基于参数估计的前向频率估计法由于直接对接收信号进行处理，因此估计速度快，而且没有反馈支路，不会出现挂起现象，很适合突发信号载波频偏估计。经典的前向频率估计算法有Kay算法、Fitz算法、L＆R算法、M＆M算法等。Kay算法采用了信号相位差加窗进行估计的方法，仅能在高SNR条件下获得较高的估计精度［2］。文献［3］对Kay算法进行了改进，通过对相位差加权平均，降低了SNR阈值。但随着平均次数的增加，其估计精度会显著降低。Fitz算法［4］和L＆R算法［5］估计精度高、估计门限低，但其估计范围小，因此仅适合于小频偏精确估计。文献［6］通过相位展开，引入Fitz算法，扩大了Fitz算法的估计范围，不过其SNR门限依然在0 dB以上。文献［7］提出了一种基于离散傅里叶变换（discrete Fourier transform，DFT）的估计方法，利用“三点法”实现快速频率估计。这种方法简单易实现，但在小样本条件下，估计精度和频率分辨率较低，且在低SNR下，其性能恶化严重。文献［8- 9］分析了相关运算对估计误差的影响，并给出了较高SNR时的相关长度最优值。文献［10- 11］给出了基于分段累加的快速傅里叶变换（fast Fourier transform，FFT）算法。由于突发信号本身较短，分段累加的优势无法体现。文献［12］依据SNR的不同，选择不同的DFT运算点数，提高了低SNR条件下的估计性能，该算法前提是已知接收信号的SNR。对于突发信号，SNR变化范围较大，且无法在很短的时间内实现SNR估计。因此，此算法同样不适用于突发信号。文献［13- 14］都是基于接收信号自相关差分对频率估计器进行改进，获得了较大的估计范围大和较高的估计精度。不过其SNR门限依然在－3 dB左右。文献［15］结合导频数据的自相关和互相关值，提出了一种应用于医疗体域网设备的低复杂度、低成本的频偏估计算法，不过该算法SNR门限要超过4 d B。文献［16］提出了一种改进的编码辅助迭代载波同步算法，大幅提高了频偏估计范围。但是迭代过程需要较长的估计时间，不适合突发信号。文献［17］针对二进制相移键控调制信号，提出了一种低计算复杂度的频偏估计算法，能够获得较大的估计范围，达到较低的SNR门限。经典的M＆M算法［18］因其实现简单、估计精度高、估计范围宽，在工程实践中得到了广泛的应用。但是其在低SNR条件下的估计精度急剧降低，估计范围也随之迅速缩小，在低SNR突发情况下应用受限。文献［19］利用DFT内插技术，能够达到与M＆M算法相当的估计性能。

为了克服现有方法普遍存在估计精度、估计范围、SNR门限之间的矛盾，本文提出了一种有数据辅助的接收信号自相关序列离散傅里叶变换（auto correlation DFT，ACDFT）的载波频偏估计算法。

1 问题建模

1.1 信号模型

假设接收信号为多进制相移键控（M-ary phase shift keying，MPSK）调制信号，信道为理想的高斯白噪声信道，其双边功率谱密度为N0／2，符号定时能够理想同步。接收机本地参考频率与载波频率的偏差为Δf Hz。那么经过匹配滤波和正确的采样，得到的第k个符号为

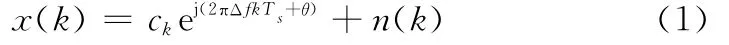
式中，｛ck｝为幅度为1的符号序列；Δf为残留载波频偏；Ts为符号周期；θ为载波初始相位；｛n（k）｝为0均值、独立同分布的复高斯随机变量。假定符号SNR为Es／N0，则噪声方差为1／（Es／N0）。在有数据辅助的情况下，｛ck｝为已知序列。在符号同步的情况下，显然可以将x（k）乘以（为ck的共轭），去除符号带来的影响，记

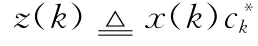
则

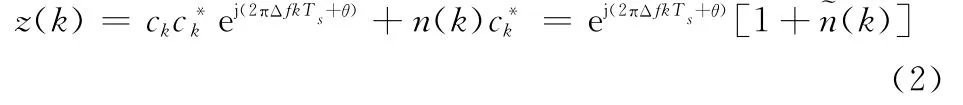
换言之，载波频率估计也就是利用混有噪声的L个连续采样点｛z（k），1≤k≤L｝，得到频偏估计值Δ^f。

1.2 性能指标

评价一个载波频偏估计算法性能优劣，通常包括估计精度、估计范围以及计算量等指标。估计精度常用归一化方差var（ΔTs）或者归一化均方根误差（normal root mean square error，NRMSE）来衡量。其中NRMSE定义如下：

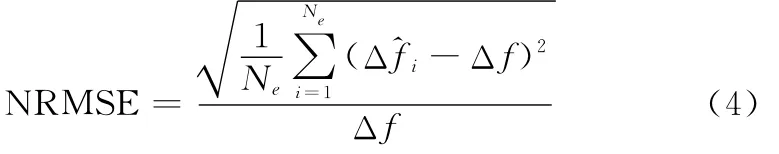
式中，Ne为实验次数；Δ表示第i次实验结果。

对于低SNR情况下突发信号的载波频偏估计，还应考虑算法适用的SNR门限SNRth（也可以用门限Eb／N0衡量）、差错概率pr等指标。所谓差错概率就是估计结果误差绝对值超过一定门限Δfth（取决于具体的应用，比如数倍克拉美罗界）的概率，定义如下：

SNR门限就是在差错概率不超过一定的门限prth的前提下，算法能够正常工作的最低SNR，定义如下：

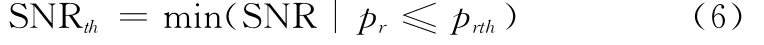
2 算法描述

2.1 基于自相关的频率估计算法性能分析

作为前向频率估计方法的一个重要类型，基于自相关函数的频率估计方法被广泛应用于突发信号载波频偏估计。首先对样点序列｛z（k）｝计算其部分自相关，如下：

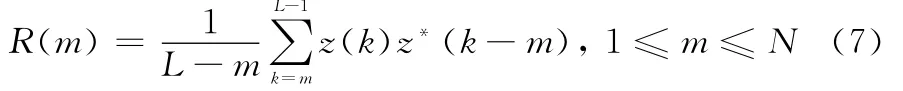
式中，N为参与频率估计的自相关样点数。通常情况下，N≤L／2，在Fitz、L＆R、M＆M等算法中，N＝L／2时算法性能最优。

将式（2）代入式（7），重新写为

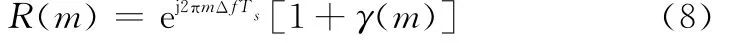
式中

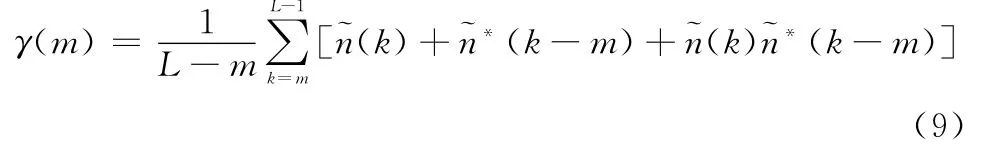
由此可见，接收序列的自相关序列中包含了载波频偏信息和噪声。Fitz、L＆R、M＆M等经典算法都是对该序列进行不同的处理而得到的。相较其他算法，M＆M算法具有较宽的估计范围、较高的估计精度和较低的SNR门限。在下文中，重点对M＆M算法进行分析，本文提出的算法也主要与其进行性能比较。M＆M算法在一定的SNR要求下，忽略掉式（8）中最后一项，得到频偏估计值为

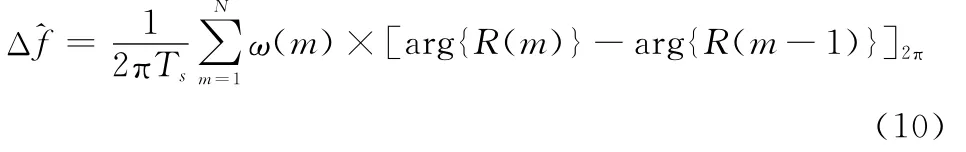
式中，ω（m）为平滑函数［18］，实质上是一个权重因子，其在M＆M算法中起着非常关键的作用。

M＆M算法在SNR较高时，其估计结果能够接近或者达到修正的克拉美罗界（modified Cramer-Rao bound，MCRB）［20］。当SNR降低至某一阈值时，估计性能急剧恶化。如图1所示，对正交相移键控（quadrature phase shift keying，QPSK）调制信号，在L＝128、N＝64、fs＝4 k Hz条件下，当Eb／N0≤－5.5 d B时，算法性能急剧恶化。

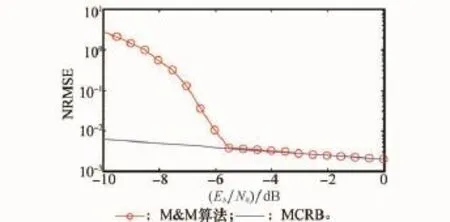
图1 低SNR情况下M＆M算法频偏估计性能

2.2 AC-DFT算法描述

M＆M算法的基本思想与其他基于相位差分频率估计的算法相似，在SNR较高的条件下，把复加性噪声等效到相位中去，从而忽略噪声对频率估计的影响。正如前面分析，这种算法在低SNR情况性能将急剧恶化，甚至根本无法使用。为了提高低SNR下的估计性能，本文直接对自相关值进行DFT分析（在实际使用中可用FFT来实现），得到频偏估计结果，将这种算法称为基于自相关序列离散傅里叶变换的载波频偏估计算法——AC-DFT算法。由于本算法直接从式（8）进行频偏估计，在低SNR情况下，能够获得比M＆M算法更好的估计性能。具体实现步骤如下：

步骤1对样点序列｛z（k）｝计算其自相关，得到长度为2L－1的自相关序列R（n）

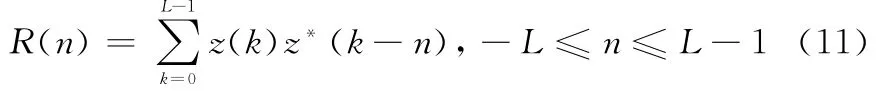
步骤2 将｛R（n）｝向右平移L个点，进行加窗处理，取中间的M个相关值（M≤2L－1，且为偶数），并对幅度进行归一化处理，得到长度为M的部分自相关序列｛R（m）｝

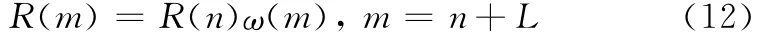
式中，ω（m）为m＝0，1，…，M。

窗函数定义如下：

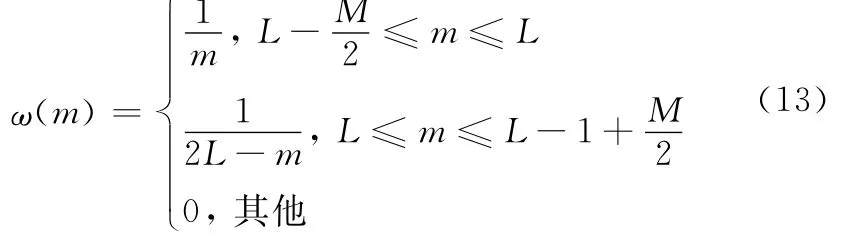
步骤3对｛R（m）｝做M点的DFT，得到｛R（k）｝

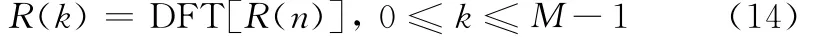
步骤4进行频偏估计，得到频偏估计值为

式中，kpeak＝k＋δ，k＝arg max（｜R（k）｜），表示｛R（k）｝峰值对应的序号，δ为修正因子［6］，定义如下：

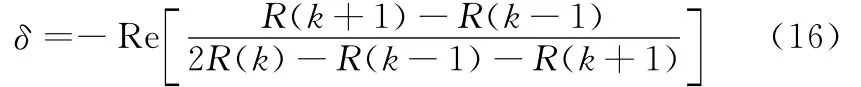
式中，Re［·］表示取实部。

由于该算法也是基于式（8）进行估计，其估计范围同样为｜Δ｜≤0.5fs。

2.3 自相关样点数的选择

对于M＆M等算法，自相关样点数N＝L／2时性能最优，且样点数的选择对算法性能有较大的影响［18］。由于自相关值呈三角形分布，也就意味着m值越大的自相关值受噪声影响越大，因此，过多的样点数，会导致SNR门限升高。而为了获得较高的估计精度，需要足够多的样点数。而越多的样点数，意味着更高的计算复杂度。图2给出了AC-DFT算法在不同自相关样点数下的估计性能。由图可见，对于AC-DFT算法，随着自相关样点数的增加，估计精度不断提高。不过当M≥L以后，性能提升将不太明显。在低SNR情况下，M＝5L／4时能够获得更低的SNR门限和更高的估计精度。因此，在实际使用中，样点数的选择需要综合考虑估计精度、SNR门限和计算复杂度。

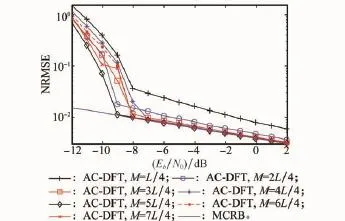
图2 AC-DFT算法在不同自相关样点数下的NRMSE曲线

3 仿真实验与性能分析

3.1 仿真条件

为了考察AC-DFT算法的性能，利用Matlab软件进行仿真，重点将其与M＆M算法以及MCRB进行比较。其中，MCRB［20］计算方式如下：

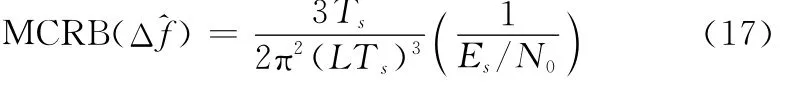
仿真过程中，假设接收到的突发信号采用QPSK调制，真实的载波频偏Δf＝200 Hz，用于载波频偏估计的信号时长T＝32 ms，默认符号速率fs＝4 k Hz，部分相关样点数N＝L／2、M＝5L／4。

3.2 仿真实验

利用Matlab软件对M＆M算法和AC-DFT算法进行10 000次蒙特卡罗仿真，实验结果及性能分析如下。

（1）估计精度

在上述仿真条件下，L＝128，N＝64，与文献［18］选择的参数完全相同。图3给出了M＆M算法和AC-DFT算法在不同SNR下NRMSE。由图可见，在Eb／N0≥－5.5 dB时，两种算法基本都能接近或者达到MCRB。换言之，在SNR较高的时候，AC-DFT算法具有与M＆M算法相当的估计精度。当Eb／N0≤－5.5 dB时，M＆M算法的估计性能随SNR的降低急剧恶化，而AC-DFT算法可低至－9.5 dB，比M＆M算法低4 dB。

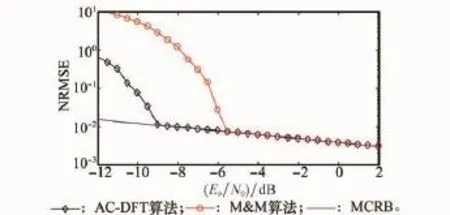
图3 不同信噪比下的NRMSE曲线

（2）错差率和SNR门限

图4给出了不同估计误差门限下，差错率与SNR的关系。由图4可见，在低SNR情况下，对相同的误差门限，AC-DFT算法的差错率明显低于M＆M算法。此外，在误差门限和差错概率一定的条件下，比如，Δfth＝2MCRB、prth＝10%，由图可见，对M＆M算法和AC-DFT算法的门限Eb／N0分别为－8 dB和－12.5 dB。改变误差门限和差错概率的约束条件，也能得到类似的结果。也就是说，AC-DFT算法的工作门限比M＆M算法低4 dB以上。

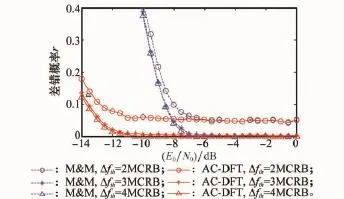
图4 不同载噪比下的差错率曲线

（3）估计范围

M＆M算法和AC-DFT算法的理论估计范围均为｜Δ^f｜≤0.5fs，且在SNR较高的情况下，两种算法都能达到最大的估计范围。由于两种算法的SNR门限不一致，所以在低于M＆M算法门限SNR下，比较二者的估计范围将没有实际意义。为了衡量算法的实际估计范围，分别在二者的SNR门限上进行仿真。图5给出了两种算法在各自的门限SNR下的归一化频差Δf／fs与归一化估计频差Δ^f／fs之间的关系曲线。由图可见，M＆M算法在门限SNR附近，实际的估计范围降低为0.4fs，而AC-DFT算法依然能达到0.5fs。意味着在各自的门限SNR附近，AC-DFT算法能够获得理论上估计范围，而M＆M算法的实际估计范围要小于理论值。

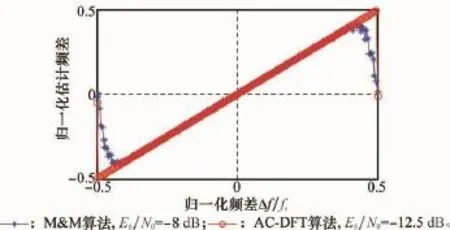
图5 估计范围

（4）符号速率对估计范围的影响

对于特定的突发信号，用于载波频偏估计的信号时长以及载噪比是确定的，符号速率也往往是确定的。但在某些场合下，可以自主设置符号速率。由于不同的符号速率对应不同的采样点数，符号速率的选择将对估计性能产生一定的影响。图6给出了不同符号速率下，NRMSE与载噪比的关系。由图6可见，在低载噪比情况下，两种算法估计精度都随着符号速率的增加而降低，但是高符号速率下，AC-DFT算法具有更低的SNR门限，且符号速率对估计精度的影响不如M＆M算法明显。由于算法的估计范围与符号速率成正比。因此，在低SNR情况下，AC-DFT算法可以通过提高符号速率fs来进一步扩大估计范围。如图6所示，在门限SNR附近，AC-DFT算法能够获得数倍于M＆M算法的估计范围。

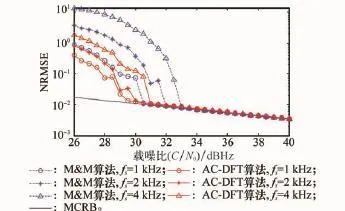
图6 不同符合速率下的NRMSE曲线

4 结论

相比其他算法，本文提出的AC-DFT算法虽然计算复杂度有所增加，不过随着硬件处理能力的提高，利用FPGA等完成FFT已经非常便捷，计算复杂度已不是制约算法性能的瓶颈。该算法能够获得更低的SNR门限、更低的差错概率、更宽的估计范围，非常适合低SNR突发信号载波频偏估计。该算法除了应用于突发通信信号载波频偏估计外，也可用于低SNR情况下导航以及雷达信号处理等领域的频偏估计。

［1］Song Q P，Liu R K.A frequency estimation algorithm for high dynamic and weak signal in deep space［J］.Journal of Astronautics，2013，34（11）：1496- 1501.（宋青平，刘荣科.一种用于深空高动态微弱信号的频率估计算法宋青平［J］.宇航学报，2013，34（11）：1496- 1501.）

［2］Kay S.A fast and accurate single frequency estimator［J］.IEEE Trans. on Acoust，Speech，Signal Processing，1989，37（12）：1987- 1990.

［3］Kim D Y，Narasimha M J.An improved single frequency estimator［J］. IEEE Trans.on Signal Processing，1996，3（7）：212- 214.

［4］Fitz M P.Further results in the fast estimation of a single frequency［J］. IEEE Trans.on Communications，1994，42（234）：862- 864.

［5］Luise M，Regginnaini R.Carrier frequency recovery in all-digital modems for burst mode transmissions［J］.IEEE Trans.on Communications，1995，43（2）：1169- 1178.

［6］Liu X D，Chen W D.Carrier frequency offset estimation algorithm with extended range and high accuracy［J］.Radio Engineering of China，2014，44（3）：43- 45.（刘晓冬，陈卫东.一种宽范围高精度的载波频偏估计算法［J］.无线电工程，2014，44（3）：43- 45.）

［7］Jacobsen E，Kootsookos P.Fast，accurate frequency estimators［J］.IEEE Signal Processing Magazine，2007，24（3）：123- 125.

［8］Volcker B，Handel P.Frequency estimation from proper sets of correlations［J］.IEEE Trans.on Signal Processing，2002，50（4）：791- 802.

［9］Rosnes E，Vahlin A.Frequency estimation of a single complex sinusoid using a generalized Kay estimator［J］.IEEE Trans.on Communications，2006，54（3）：407- 415.

［10］Brown T，Wang M M.An iterative algorithm for single-frequency estimation［J］.IEEE Trans.on Signal Processing，2002，50（11）：2671- 2682.

［11］Zhang X W，Li Y Y，Meng F M.Research of segmented autocorrelation frequency estimation algorithm［J］.Application Research of Computers，2014，31（1）：92- 94.（张晓威，李洋洋，孟凡明.分段自相关频率估计算法研究［J］.计算机应用研究，2014，31（1）：92- 94.）

［12］Yang D Z，Song N F，Lin Z L，et al.High-accuracy frequency estimation algorithm based on autocorrelation and phase difference method［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（8）：1030- 1033.（杨德钊，宋凝芳，林志立，等.基于自相关及相位差法的高精度频率估计算法［J］.北京航空航天大学学报，2011，37（8）：1030- 1033.）

［13］Shuai T，Ren Q Y，Liu J，et al.An frequency estimator for large frequency offset and low SNR signals［J］.Journal of Astronautics，2010，31（12）：2741- 2745.（帅涛，任前义，刘静，等.一种适用于大频偏和低信噪比条件的频率估计器研究［J］.宇航学报，2010，31（12）：2741- 2745.）

［14］Zhou L L，Luo J F，Fu Y X，et al.A frequency estimator based on autocorrelation function in low SNR circumstance［J］.Journal of Huazhong University of Science and Technology（Nature Science），2014，42（4）：45- 49.（周磊磊，罗炬锋，付耀先，等.低信噪比下基于自相关函数的频率估计方法［J］.华中科技大学学报（自然科学版），2014，42（4）：45- 49.）

［15］Li N，Lin W L，Tu S，et al.A low-complexity frequency-offset estimation algorithm for the medical body area［C］∥Proc.of the IEEE International Conference on Network Infrastructure and Digital Content，2012：554- 557.

［16］Shen H O，Wang Y M，Xu H.A modified code-aided carrier synchronization algorithm［J］.Journal of Chongqing University of Posts and Telecommunications（Natural Science Edition），2013，25（3）：324- 328.（沈海鸥，王永民，许华.一种改进的编码辅助载波同步算法［J］.重庆邮电大学学报（自然科学版），2013，25（3）：324- 328.）

［17］Le T，Wang J B.An algorithm for carrier frequency offset estimation in BPSK burst transmission［C］∥Proc.of the IEEE International Conference on the Applications of Digital Information and Web Technologies，2014：50- 53.

［18］Mengali U，Morelli M.Data-aided frequency estimation for burst digital transmission［J］.IEEE Trans.on Communications，1997，43（1）：23- 25.

［19］Zhu Q K，Xu Y，Liu D X，et al.A high-precision carrier frequency offset estimation algorithm based on DFT［J］.Journal of Naval Aeronautical and Astronautical University，2014，29（4）：329- 334.（朱乾坤，许阳，刘东鑫，等.一种基于DFT的高精度载波频偏估计算法［J］.海军航空工程学院学报，2014，29（4）：329- 334.）

［20］Aldo D，Umberto M，Ruggero R.The modified Cramer-Rao bound and its applications to synchronization problems［J］.IEEE Trans.on Communications，1994，42（234）：1391- 1399.

Carrier frequency offset estimation algorithm for burst and low SNR signal

ZHAO Lu-wen1，ZHANG Bei-jiang1，MIAO Zhi-min2，LI Guang-xia1，LIU Bo1
（1.Communication Engineering College，PLA University of Science and Technology，Nanjing 210007，China；2.Command Information System College，PLA University of Science and Technology，Nanjing 210007，China）

Fast and accurate carrier frequency offset estimation is very important in the coherent demodulation for the burst signal.There are some dilemmas in the traditional carrier frequency estimation algorithm，such as estimation accuracy，signal-to-noise ratio（SNR）threshold and estimation range，etc.Aim to these problems，a data aided carrier frequency offset estimation algorithm for burst and low SNR signal is put forward based on the discrete Fourier transform（DFT）of the auto correlation of the

signal.The carrier frequency offset can be estimated by windowing to the received signal autocorrelation and DFT.The simulation results show that，compared with the M＆M algorithm，the lower SNR threshold，lower error probability and higher estimation range in the low SNR conditions are achieved for the algorithm.It is very suitable for carrier frequency offset estimation for the burst and low SNR signal.

carrier frequency offset estimation；low signal to noise ratio（SNR）；burst signal；M＆M algorithm

N 911

10.3969／j.issn.1001-506X.2015.12.28

赵陆文（1977- ），男，讲师，博士，主要研究方向为卫星导航、卫星通信。

E-mail：zhaoluwen＠163.com

张北江（1977- ），男，讲师，主要研究方向为卫星导航、卫星通信。

E-mail：zhang_bei_jiang＠163.com

缪志敏（1978-- ），女，讲师，博士，主要研究方向为人工智能、模式识别。

E-mail：oilvermiao＠126.com

李广侠（196-4- ），男，教授，博士研究生导师，主要研究方向为卫星导航、卫星通信。

E-mail：13905177686＠189.com

刘波（1967- ），男，教授，主要研究方向为卫星导航、卫星通信。