平台-平台惯性系统传递对准技术

2015-06-05李蝉,余浩章,张士峰

系统工程与电子技术 2015年12期

平台-平台惯性系统传递对准技术

李蝉1，2，余浩章2，张士峰1

（1.国防科学技术大学航天科学与工程学院，湖南长沙410073；2.北京跟踪与通信技术研究所，北京100094）

分析了平台-平台系统传递对准技术与捷联捷联系统传递对准技术的差异，在此基础上，推导了平台-平台传递对准中主、子惯导系统速度误差方程和框架角误差方程，建立了平台平台传递对准数学模型，给出了角速度与角加速度的获取方法，设计的低通滤波能够有效抑制角速度与角加速度中的高频噪声。仿真计算表明，基于速度与框架角匹配的平台平台传递对准方法能够得到优于0.15°的对准精度。

传递对准；平台式惯性系统；速度匹配；框架角匹配；低通滤波器

0 引言

传递对准是指载体在航行时，利用高精度的主惯导系统信息对载体上需要对准的子惯导系统进行初始对准的方法，该方法是目前解决运动载体上武器系统在动基座条件下初始对准问题的主要手段。传递对准技术经过几十年的发展，在误差模型［1-2］、匹配方式［35］、可观测性分析［67］、杆臂效应及弹性变形［8-9］等方面取得了许多成果，传递对准的快速性与精度得到了很大提高。在工程实际中，传递对准技术成功应用于战术导弹、飞机、舰船等对象上［34，8，10］，但是这些对象及研究内容绝大多数使用捷联惯性系统，即主、子惯导系统均为捷联惯性系统，或子惯导系统为捷联惯性系统。出于应用背景等原因，国内外关于潜艇潜射导弹、天基武器系统、舰载机着陆等平台平台惯性系统的传递对准问题，即主、子惯导系统均为平台式系统的情况，公开文献讨论较少。文献［11］讨论了舰载平台系统的传递对准，其数学模型仍然基于捷联系统获得。文献［12］研究了平台系统的姿态传递对准问题。

实际上，平台-平台传递对准技术不同于捷联系统传递对准技术，主要特点在于：

（1）平台式惯性系统有物理平台与框架系统，载体角运动可由框架系统补偿，因此平台式惯性系统可实现惯性空间定向；

（2）平台系统不能直接给出载体角速度信息，只能给出框架角信息，而且框架角信息不是通过数学方法计算得到的，而是平台伺服回路与框架系统直接给出的，所以平台系统的失准角概念与捷联系统有所不同；

（3）传递对准中杆臂效应的补偿需要得到载体角速度与角加速度，而平台系统只能输出框架角（即姿态角），如何准确补偿杆臂效应也是其中的关键问题；

（4）平台式惯性系统一般应用于大型舰船、潜艇、战略导弹等对象，其载体机动方式与大小受到很大限制，降低了传递对准中系统的可观测性。

本文主要开展平台-平台系统传递对准数学模型、杆臂效应补偿、方案实现等方面的研究，由平台式系统导航数学模型出发，建立传递对准速度及框架角误差微分方程，在此基础上提出平台平台传递对准匹配方法，最后仿真研究平台平台传递对准中的对准精度与对准速度。

1 平台式惯性系统导航数学模型

为了描述方便起见，定义如下几个坐标系：i表示惯性坐标系，e表示地心坐标系，n表示导航坐标系（当地地理坐标系，即北天东坐标系），m表示主惯导导航坐标系，s表示子惯导实际导航坐标系，s¯表示子惯导考虑安装误差情况下实际三轴指向形成的坐标系，b表示载体坐标系。由于子惯导系统安装误差，m系与s系并不重合，而由于子惯导系统漂移误差，导致s系与s¯系不重合。

惯性平台导航系统可实现对惯性空间定向，同时也可跟踪当地地理坐标系，这种导航方式可直接给出当地地理经、纬度。在讨论平台-平台传递对准问题时，假定主、子平台系统都跟踪当地地理坐标系，即指北跟踪平台。指北跟踪平台系统的导航方程可写成如下形式：

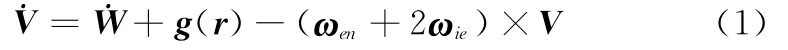
式中，ωie为地球自转角速度在地理坐标系中的表示；ωen为地理系相对于地心坐标系的角速度，即载体在球面上航行所形成的角速度。

平台式系统为保证台体的空间指向，通过框架系统运动补偿载体角运动，可直接给出框架角，框架角信息与载体系至导航系的姿态转换矩阵密切相关，但框架角信息并不是通过数学方法计算得到的，而是平台伺服回路与框架系统直接给出的，因此平台系统的失准角概念需要重新定义。记α，β，γ分别为平台基座相对外框架、外框架相对于内框架、内框架相对于台体的转角。根据台体及框架坐标系的定义，给出框架角速度与载体角速度及台体角速度的关系［13］：

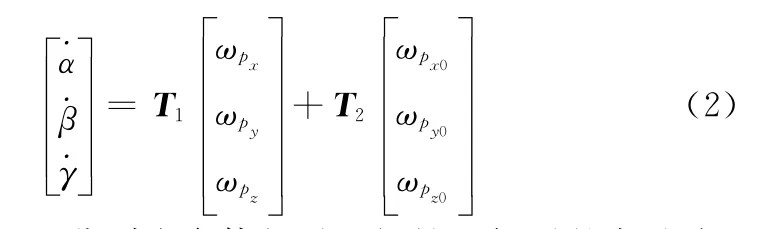
当平台取这种定向方式时，载体姿态角与平台框架轴是一一对应的，不需要经过坐标变换便可用平台姿态角传感器的信号度量载体姿态角。

2 平台-平台系统传递对准误差模型

平台系统采用实际物理平台，姿态角（框架角）输出由平台回路系统得到，而且平台式惯导系统无法直接给出载体角速度，只能给出框架角输出。在平台-平台传递对准过程中，能直接得到的信息是速度信息与框架角信息，下面推导给出平台平台传递对准速度与框架角误差微分方程数学模型。

2.1 惯性器件误差模型

由于传递对准时间较短，子惯导加速度计和陀螺仪的漂移量较小，相当一部分惯导工具误差系数项引起的测量误差很小。如果要对所有误差系数都建模并加以估计，一方面降低了系统的可观性，另一方面大大增加了滤波的状态维数和计算量，降低了安装误差角的估计精度，所以在传递对准过程中，认为子惯导仪器的测量误差主要由常值偏差和白噪声构成。即有

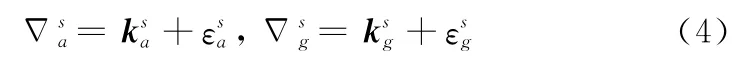
2.2 速度误差方程

在传递对准中，主惯导系统一般不考虑惯性器件漂移误差，其速度微分方程为

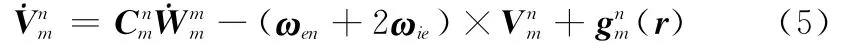
对于子惯导系统，其比力信息是在子惯导真实坐标系中测量得到的，其导航方程为

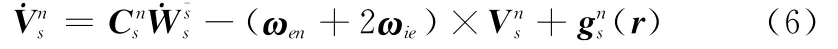
子惯导系统敏感到的比力是在其自身敏感轴所在坐标系中得到的，可表示为

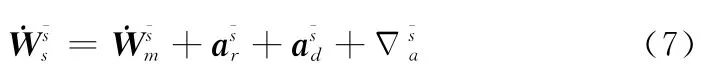
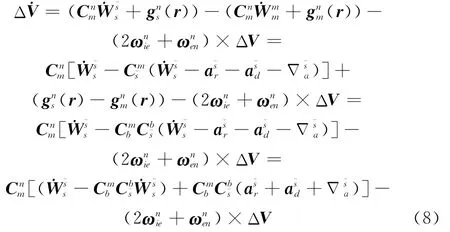
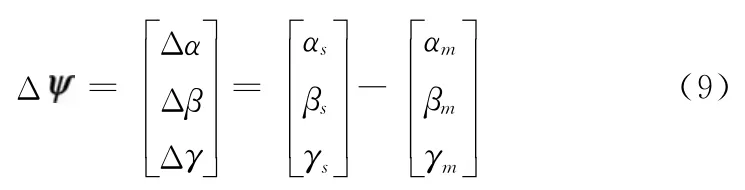
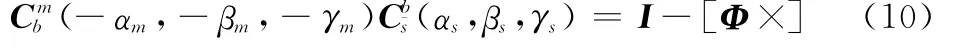
式中，Φ为两个坐标转换矩阵之间的失准角。假设平台框架角与弹体姿态角（俯仰、偏航、滚转）的关系为式（3），根据失准角与姿态角的概念，失准角Φ与Δ之间的关系为

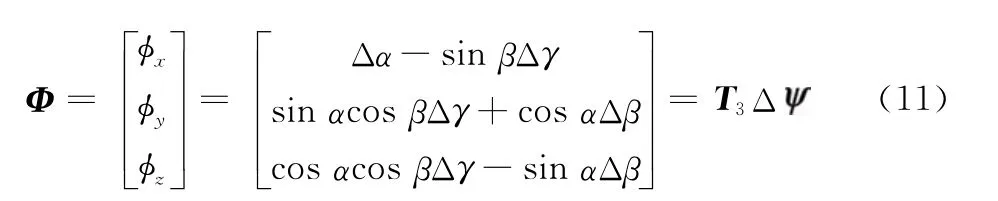
式中

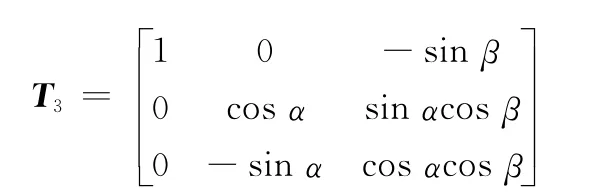
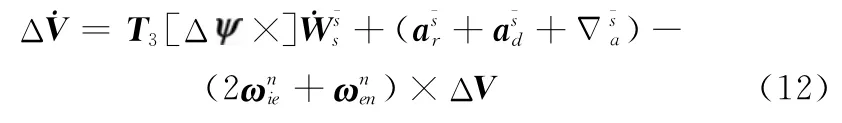
2.3 框架角误差方程

对于指北跟踪平台而言，平台台体角速度与载体角速度共同构成了框架角输出。对于主惯导而言，由于导航坐标系为地理坐标系，则台体跟踪角速度

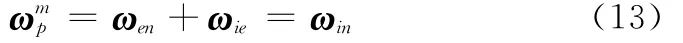
基座角速度即载体运动角速度，即

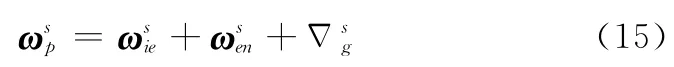
必须说明的是，子惯导敏感到的基座角速度与子惯导安装误差角密切相关，其基座角速度是在子惯导坐标系s下测量的。根据框架系统原理，子惯导陀螺仪漂移量不会反映到平台系统的伺服回路中，所以主、子惯导敏感到的载体角速度为

假设子惯导系统相对于主惯导系统的安装误差为δs，令＝［αβγ］T，则主、子惯导系统框架角输出之差为

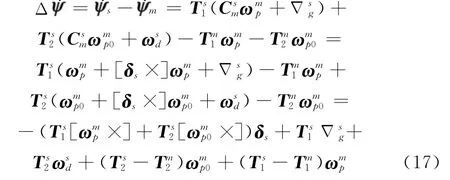
2.4 杆臂效应补偿

在平台-平台系统传递对准中，载体一般为大型舰艇，杆臂矢量rs比较大，导致杆臂效应产生的主、子惯导加速度差也比较大，而且由于各种环境等因素的限制，载体机动加速度比较小，使得杆臂加速度补偿更加重要。定义杆臂加速度如下：

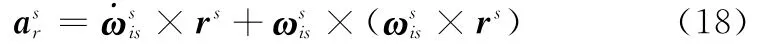
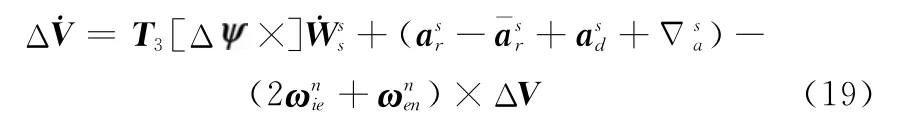
2.5 平台-平台传递对准估计

实际上，式（17）和式（19）就是平台平台系统传递对准中的速度误差微分方程与框架角误差微分方程，为避免滤波系统模型中待估参数过多、模型过于复杂，主、子惯导系统框架角、主惯导敏感到的载体摇摆角速度、以及台体角速度都不作为系统状态变量。在滤波过程中，、中的框架角参数直接使用子惯导系统输出代替，中的框架角参数直接使用主惯导系统输出代替，而主惯导敏感到的载体摇摆角速度、台体角速度根据主惯导输出框架角实时计算得到，这样，传递对准模型中的系统变量为

平台系统不能直接输出角速度信息，载体的角速度信息只能反映到框架角输出上，但是在传递对准中，姿态误差微分方程以及杆臂加速度的补偿都需要角速度信息，因此如何获取角速度信息是平台平台传递对准中非常关键的问题。考虑主惯导平台框架角输出方程式（2），对于跟踪地理坐标系的平台系统而言，ωpx、ωpy、ωpz可根据地球自转角速度及主惯导系统获得速度信息得到，见式（13）。而基座角速度ωpx0、ωpy0_、_ω____pz0的获取则需要采取一定的措施，可根据主惯导系统输出的框架角信息实时估计基座角速度。由于平台台体角速度已知，可利用下式得到载体角速度。

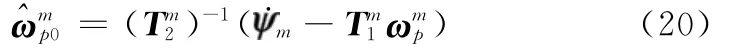
对于差分角速度，设计如下的低通滤波器：通带频率为信号频率的0.05倍，阻带频率为信号频率的0.2倍，通带衰减不得高于3 d B，阻带衰减不得低于40 d B，得到的滤波器离散传递函数为

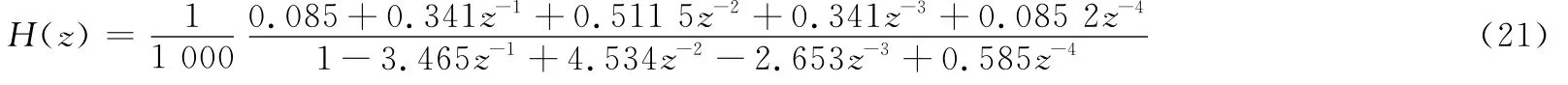
式中，z为复变量。

对于差分角加速度，设计如下的低通滤波器：通带频率为信号频率的0.01倍，阻带频率为信号频率的0.2倍，通带衰减不得高于3 d B，阻带衰减不得低于40 dB，得到的滤波器离散传递函数为

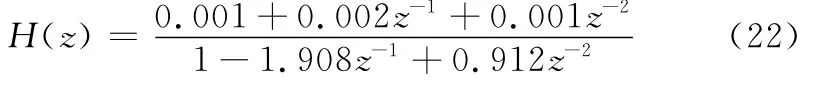
3 速度+框架角匹配方法

3.1 速度匹配方程

式中，εvx、εvy、εvz均表示白噪声。

3.2 框架角匹配方程

获得主、子惯导框架轴测量值后，实际上可以给出舰体坐标系相对于惯性坐标系的坐标转换矩阵，直接将二者作差，即得到主、子惯导系统姿态误差角。

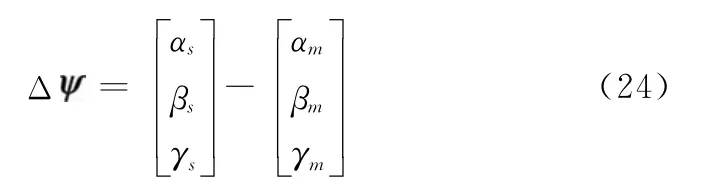
4 仿真验证与分析

速度与角速度匹配模式下，系统的状态方程为15维，分别为主、子惯导系统速度差ΔV、失准角误差Δ、安装误差δs、加速度计零偏、陀螺仪零偏，即

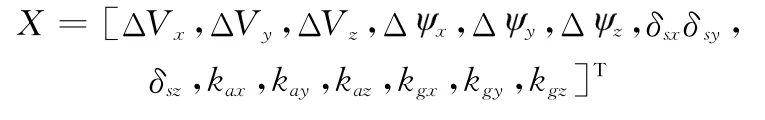
动力学模型为式（17）和式（19），匹配方程为速度误差匹配方程式（23）、平台姿态角匹配方程式（24）。需要注意的是，杆臂效应的补偿需要得到载体角速度信息，但平台系统不能直接获得角速度，所以角速度需要在滤波过程中实时计算得到。

仿真初始参数设置：主子惯导间杆臂矢量（单位：m）rs＝［10 10 2］T；子惯导误差参数：加速度计零偏（单位：m／s2）＝［0.000 1 0.000 1 0.000 1］T，加速度计测量噪声标准差10－5m／s2，陀螺仪常值偏值（单位：（°）／h）＝［0.2 0.2 0.2］T，陀螺仪测量噪声标准差0.005°／h；子惯导的安装误差角δs＝［1° 1° 0.8°］，速度匹配噪声标准差10－4m／s，框架角输出测量噪声10″；主惯导系统加速度计与陀螺仪零偏及随机误差都假设为零，框架角输出测量噪声假设为5″。这里不考虑舰船弹性变形的影响。

载体机动方式是对传递对准精度与速度有重要影响，以舰船为背景讨论平台平台传递对准问题。由于海浪及洋流的影响，舰船在海洋中存在自然的三轴角运动，在仿真中，假设舰船3个方向的角运动分别由两种频率的摇摆运动合成，其中航向角θA（自北向东转为正）的两种摇摆周期分别为18 s、13 s，对应振幅分别为3.5°、2°，偏航运动周期分别为19 s、13 s，对应振幅分别为0.7°、0.2°，俯仰运动周期分别为19 s、14 s，对应振幅分别为3°、1.5°。对准时间为120 s。

根据式（20）获得载体角速度，由于主惯导精度较高，随机误差较小，所以这里利用主惯导框架角输出得到角速度与角加速度，然后根据式（18）计算杆臂效应加速度，在滤波中进行补偿。设定信号采样频率为20 Hz，主惯导框架角随机误差为5″，两次差分周期为0.05 s。图1是根据一次差分得到的角速度值。图2是根据两次差分得到的角加速度值。可以看出，角加速度高频噪声非常大，达到0.4 rad／s，主要原因是主惯导框架角随机测量噪声经过两次差分后被急剧放大。

采用前面设计的差分角速度低通滤波器，滤波结果如图3所示；采用前面设计的差分角加速度低通滤波器，滤波结果如图4所示。可以看出，通过低通滤波器后，高频信号被有效滤除，保留了低频信号，在仿真中，舰船摇摆运动周期在15 s左右，在100 s的仿真时间中，约有6～8个周期的变化。图4中信号的周期特性与仿真设置相符，说明低通滤波器设计比较合理。

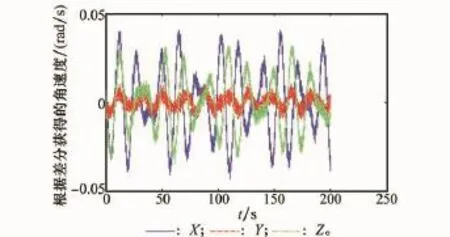
图1 根据一次差分得到的角速度值

图2 根据两次差分获得角加速度值

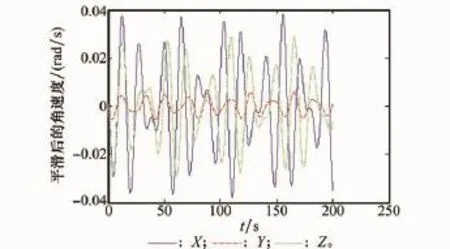
图3 滤波后的角速度值

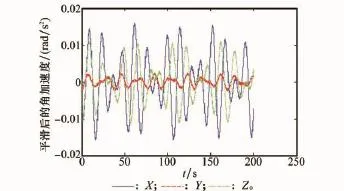
图4 通过低通滤波器后的角加速度值

通过上述低通滤波器后，计算得到的径向加速度与切向加速度值中的高频噪声被有效滤除，计算结果见图5、图6。可以看出，切向加速度远大于径向加速度，所以杆臂效应的补偿中，切向加速度的补偿更需注意，但切向加速度需要计算角加速度，要获得高精度的角加速度值，对于仅有框架角输出的平台系统而言是比较困难的。

进一步分析表明，通过对主惯导框架角输出差分获得角速度，能够有效补偿向心加速度，对于切向加速度，低通滤波器能够有效地滤除高频噪声，显著减小切向加速度的随机干扰，但信号通过低通滤波器，信号存在一定的失真与延迟，与真实值存在一定的差异，这种差异影响了平台-平台传递对准精度。

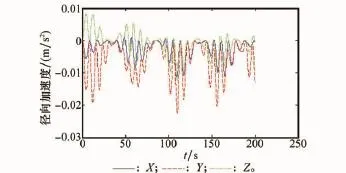
图5 通过低通滤波器后的径向加速度值

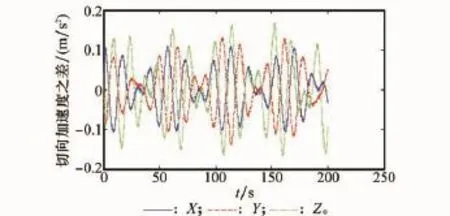
图6 通过低通滤波器后的切向加速度值

图7～图10是补偿杆臂加速度后的传递对准滤波图。从中可以看出，由于切向加速度补偿精度不高，使得子惯导加速度计零偏和陀螺仪估计精度不高，这是容易理解的。另一方面，由于测量噪声以及杆臂补偿误差造成陀螺仪零偏估计偏差较大。但子惯导安装误差传递对准收敛速度比较快。杆臂效应产生的主要原因是潜艇受到海浪影响产生的三轴摇摆，从而产生较大的杆臂效应加速度。

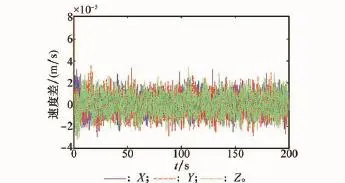
图7 杆臂效应补偿后的速度差滤波图

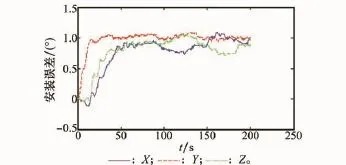
图8 杆臂效应补偿后的安装误差滤波图

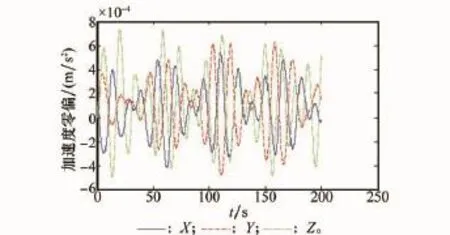
图9 杆臂效应补偿后的加速度零偏滤波图

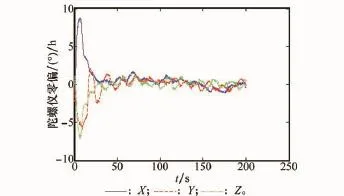
图10 杆臂效应补偿后的陀螺仪零偏滤波图

为减小仿真过程中随机数的影响，利用蒙特卡罗方法进行了100次仿真，取滤波收敛后倒数20 s的估计结果进行统计计算，表1给出了考虑杆臂效应补偿情况下100次仿真结果的统计值。从表1中可以看出，基于速度和框架角匹配的平台-平台传递对准方案可实现0.15°的对准精度。

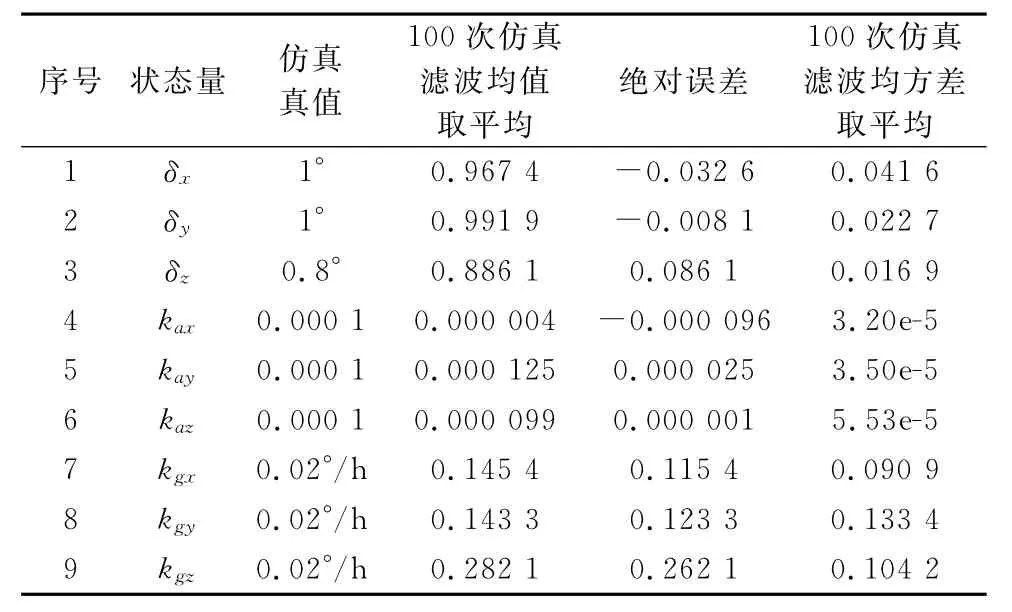
表1 考虑杆臂效应补偿的仿真滤波结果统计分析

5 结论

对于平台-平台系统传递对准技术而言，与捷联系统传递对准技术有比较大的区别，通过上述分析，有以下几点结论：

（1）由于平台系统无法直接获取角速度，需要通过差分得到，因此角速度匹配无法使用。为实现杆臂效应补偿，需要对框架角进行差分计算，而差分计算放大了框架角测量随机噪声，需要对差分得到的角速度与角加速度进行低通滤波，本文设计的低通滤波器很好的抑制了高频噪声，能够很好地复现真实的杆臂效应加速度。仿真计算表明，使用速度和框架角匹配方案传递对准精度可达到0.15°。

（2）平台-平台传递对准中，必须同时补偿杆臂效应中的向心加速度与切向加速度，对于舰船的摇摆运动，切向加速度远大于向心加速度，对于这种机动强度不可能太大的情况，杆臂效应必须以较高精度补偿。

（3）舰船的摇摆运动是平台平台传递对准中一种非常有益的机动，而且机动幅度不能太小，否则会降低传递对准精度、减缓对准速度。

［1］Goshen-Meskin D，Bar-Itzhack I Y.Unified approach to inertial navigation system error modeling［J］.AIAA Journal of Guidance，Control and Dynamics，1992，15（3）：648- 653.

［2］Gao W，Shan W，Xu B，et al.Transfer alignment of platform inertial navigation in the inertial coordinate［J］.Systems Engineering and Electronics，2015，37（5）：1151- 1156.（高伟，单为，徐博，等.惯性系下平台惯导传递方法［J］.系统工程与电子技术，2015，37（5）：1151- 1156.）

［3］Kain J E，Cloutier J R.Rapid transfer alignment for tactical weapon applications［C］∥Proc.of the AIAA Guidance，Navigation and Control Conference，1989：1290- 1300.

［4］Liu Z B，Li S H，Wang J，et al.Relative attitude matching method for transfer alignment［J］.Systems Engineering and Electronics，2014，36（8）：1619- 1625.（刘镇波，李四海，王珏，等.相对姿态匹配传递对准方法［J］.系统工程与电子技术，2014，36（8）：1619- 1625.）

［5］Liu H G，Chen G，Zhou C.Analysis of angular velocity matching transfer alignment for vessel［J］.Journal of Chinese Inertial Technology，2013，21（5）：565- 569.（刘红光，陈刚，周超.角速度匹配传递对准方法在舰艇平台的适用性分析［J］.中国惯性技术学报，2013，21（5）：565- 569.）

［6］Goshen-Meskin D，Bar-Itzhack I Y.Observability analysis of piece-wise constant systems with application to inertial navigation［C］∥Proc.of the 29th Conference on Decision and Control，1990：821- 826.

［7］Goshen-Meskin D，Bar-itzhack I Y.Observability analysis of piece-wise constant systems—part II：application to inertial navigation in-flight alignment［J］.IEEE Trans.on Aerospace and E-lectronic Systems，1992，28（4）：1068- 1075.

［8］Lyou J，Lim Y C.Transfer alignment cosidering measurement time delay and ship body flexure［J］.Journal of MechanicalScience and Technology，2009，23（1）：195- 203.

［9］Liu X，Deng Z H，Wang B，et al.Transfer alignment method under uncertain flexure deformation based on multiple model filtering［J］.Systems Engineering and Electronics，2013，35（10）：2145- 2151.（刘昕，邓志红，王博，等.不确定挠曲变形干扰下基于多模型滤波的传递对准方法［J］.系统工程与电子技术，2013，35（10）：2145- 2151.）

［10］Wang Y F，Sun F C，Zhang Y A，et al.Central difference particle filter applied to transfer alignment for SINS on missiles［J］.Aerospace and Electronic Systems，2012，48（1）：375- 387.

［11］Wang D S，Ai G B，LüS M，et al.Transfer alignment for shipboard platform inertial navigation system［J］.Journal of Chinese Inertial Technology，2009，17（1）：24- 27.（王东升，艾光彬，吕善民，等.舰载平台式惯导系统的传递对准［J］.中国惯性技术学报，2009，17（1）：24- 27.）

［12］Ding Z J，Cai H，Yang H B.Novel transfer alignment of shipborne gimbaled inertial navigation systems［J］.Transacations of the Japan Society for Aeronautical and Space Sciences，2014，57（2）：93- 100.

［13］Zhong W D.Liquid floated inertial device［M］.Beijing：China Astronautic Publishing House，1994.（钟万登.液浮惯性器件［M］.北京：中国宇航出版社，1994.）

制导与控制。

E-mail：zhang_shifeng＠hotmail.com

Transfer alignment technology of the platform inertial navigation system

LI Chan1，2，YU Hao-zhang1，ZHANG Shi-feng1
（1.College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China；2.Beijing Institute of Tracking and Telecommunications Technology，Beijing 100094，China）

The difference of transfer alignment between the platform-platform system and strapdown-strapdown system is described in detail.Then the velocity error equations and the frame angle error equations between the master platform system and the slave platform system are deduced，and the mathematical models of the platform-platform system transfer alignment are set up，and the angle velocity and angle acceleration of the vehicle are obtained by two lowpass filters which can restrain effectively the high-frequency noise in the angle velocity and the angle acceleration respectively.The final simulation result shows that the slave inertial system’s misalignment can reach an anticipated precision of 0.15 degree in 120 seconds.

transfer alignment；platform inertial system；velocity matching；frame angle matching；lowpass filter

U 666.1

10.3969／j.issn.1001-506X.2015.12.24

李蝉（198-2- ），男，工程师，博士研究生，主要研究方向为航天测控、导航制导与控制。

E-mail：lcpku＠163.com

余浩章（1977- ），男，副研究员，硕士，主要研究方向为航天测控、实验与鉴定。

E-mail：yuhaozhanghtc＠sina.com

张士峰（197-1- ），男，副教授，博士，主要研究方向为航天器动力学、

1001-506X（2015）12-2823-07

2015- 01- 15；

2015- 06- 02；网络优先出版日期：2015- 09- 07。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150907.1048.002.html