基于隐式基因混合遗传算法的多脉冲交会导引

2015-06-05欧阳高翔王小丽孙成明

系统工程与电子技术 2015年12期

关键词：脉冲数交会遗传算法

欧阳高翔，王小丽，孙成明，杨新

（1.中国科学院光电研究院，北京100094；2.北京控制工程研究所，北京100090）

基于隐式基因混合遗传算法的多脉冲交会导引

欧阳高翔1，王小丽2，孙成明1，杨新1

（1.中国科学院光电研究院，北京100094；2.北京控制工程研究所，北京100090）

针对航天器交会远程导引段时间非固定多脉冲轨道转移问题，研究多约束条件下且脉冲数未知的共面椭圆交会燃料最省导引律设计。因不同脉冲数将造成多脉冲优化问题求解变量和约束条件个数随之变化，为此在遗传算法中引入隐式基因使得种群中样本个体的基因具有长度可变特性，在单层迭代框架下可同时解出最优脉冲数和脉冲矢量。为进一步改善性能指标还将端点滑行时间作为优化变量，使得在最佳转移时刻进行离轨脉冲作用。寻优过程首先由遗传算法给出设计变量估计值，再由序列二次规划（sequential quadratic programming，SQP）求解全局最优解。最后基于主矢量和最优控制判据，表明所设计的含隐式基因混合遗传算法是求解复杂问题的有效全局优化方法，可解决一类优化变量个数可变的最优多脉冲远程导引律设计问题。

多脉冲；共面椭圆交会；隐式基因；混合遗传算法；序列二次规划；主矢量

0 引言

地球同步轨道卫星在通信、预警及电子侦察等领域起着举足轻重的作用，是空间信息链路中高价值的关键信息节点。因此对其进行监测、维修、升级与补网等空间任务具有重要意义。实施该空间任务的一项关键技术便是交会对接，其中的一类共面椭圆交会过程可描述为机动航天器从椭圆转移轨道出发，在规定时间内与共面圆轨道上的目标飞行器进行交会。常规交会过程可划分为3个阶段：调相段、远程导引段与近程逼近段，本文仅研究远程导引转移段。远程导引是指从转移轨道出发，基于事先求解的最优路径规划策略，在轨注入到追踪器后经过若干次轨道机动，逼近到目标器期望的相对距离和速度范围内［1］。另外，因某些空间紧急救援任务需要在指定时间内与目标飞行器交会，而自身携带的燃料有限，因此上述航天任务对于燃料和转移时间都有一定要求。

本文研究的共面椭圆轨道交会是以能量为性能指标，且推力、转移时间、末端时刻、位置和速度均受约束的轨道机动优化问题。该优化问题在数学上可表示为两点边值问题，可基于不同数值方法进行求解。其中，间接法需要对共轭变量的初值进行猜测，因缺乏具体的物理含义而很难确定其合理的范围，因此对于边界初值选取较为敏感，会造成算法难以收敛［2］。此外，采用配点的直接法对于配点间隔有特殊要求，经栅格化后的数值积分需要步长与配点间隔长度相匹配，否者会造成数值计算上的困难［3］。对于上述轨道优化问题中将不同长度的转移时间作为显示优化变量，若采用直接配点法极易造成数值上的不可行。作为启发式算法——遗传算法（genetic algorithm，GA）仅计算由目标函数对应的适应度值，无需导数和描述函数的自身特性等其他辅助信息，就可确定进一步的搜索方向和范围。此外，遗传算法对转移过程的时间域划分方式并不关心，目前已被广泛应用于解决轨道转移优化问题［4］。

考虑到多脉冲轨道机动在满足光照、测控和导航等条件方面具有较大的灵活性，因此工程中多采用多脉冲轨道转移方式。然而，因涉及参数较多、机动过程更复杂，以及附加其他约束时都使得上述的轨道优化求解越发困难。目前，关于多脉冲的轨道转移问题已经获得了大量的研究，对某些特定问题获得了可行方案。文献［2］通过计算主矢量值获得中间脉冲添加位置信息进行多脉冲设计，但无法考虑其他约束条件，如交会末端时刻不固定情况等。此外，大量的文献［4-8］仅关注轨道转移，而对于转移末端时刻和转移时间均受限这类交会问题未给予足够的重视。

在多脉冲交会设计中对于脉冲个数往往事先难以确定，需要综合实际约束条件后多次迭代优化获得。多脉冲交会问题从数学上可看作是多个两点边值问题的拼接，而每个两点边值问题都对应一组优化变量，且后一组变量的初始值依赖于前一组计算得到的末端值［8］。可见随着中间脉冲个数的增加，最终的优化变量个数也随之成倍增加，在脉冲数未知情况下其优化问题的困难集中体现为优化变量数可变造成数值求解的困难。文献［7］采用混合遗传算法进行多脉冲轨道转移设计，由于样本基因长度固定仅能处理脉冲个数确定的轨道转移。尽管文献［9］采用多层迭代结构进行多脉冲寻优求解，但算法结构复杂，外层优化变量若选取不当极易造成内层优化过程难以收敛。文献［10］通过引入点火开关函数的时序结构，迭代求解多点边界值问题获得最优多脉冲解，但需要人为干预。

本文借鉴文献［11］中的深空星际转移遗传优化算法，通过在常规遗传算法的基础上对样本个体添加隐式基因，使其具有某种长度可变特性，克服了传统遗传算法基因长度固定的局限，因而可处理这类优化变量个数可变的寻优问题，具体算法实现将在第2节中详细介绍。隐式基因的引入在计算上确保了种群各阶段进化操作的可行，同时缓解了传统遗传算法样本基因长度固定带来的优化困难。这种基于隐式基因的遗传优化求解在算法结构上仅为单层迭代，算法的收敛性完全与常规遗传算法一致。然而，文献［11］中隐式基因算法因其自身的概率特性，最终的优化结果存在很大的不确定性，对于转移时间、末端位置等诸多约束条件也并未加以考虑。

此外，共面椭圆交会导引不同于一般圆轨道转移，因为需要和目标星交会，它对追踪器的末端交会时刻、位置和速度均有要求。加之转移轨道为椭圆轨道，因此存在一个以燃料为基准的最佳离轨转移时刻，这里仅考虑两航天器不同初始相位差对最终寻优结果的影响。为此，在建立冲量机动模型［12］时考虑了有端点滑行等待阶段的轨道机动，即将初始滑行时间作为优化变量，寻求一系列离散时刻中最佳时间点作为离轨时刻。最后为保证算法始终运算有解，机动过程的最后两个脉冲采用Lambert方法求解［13］。当脉冲数为2时优化求解则退化为两脉冲Lambert轨道转移。考虑到遗传算法作为一种概率搜索算法，其寻优结果具有一定随机性，且随着优化参数增多极易陷入局部最优解［14］，另外也很难同时处理多约束。因此，本文设计了一种含隐式基因遗传算法与序列二次规划（sequential quadratic programming，SQP）串行的混合遗传算法，以保证最后的优化结果的确定性和全局最优性。最后，基于主矢量计算及最优控制判据，可知本文给出的混合遗传算法获得了全局最优解。

1 问题描述

多脉冲远程导引变轨任务规划问题在数学上是多个两点边值问题，其数学模型可表述为：在远程导引过程中及终端的各种等式、不等式约束下，规划变轨物理量——初始端滑行时间、变轨次数、变轨时刻、冲量方向和冲量大小，使其给定的推进剂消耗性能指标最优，这里脉冲数事先不确定。另外，因转移轨道的偏心率造成不同初始相位差在相同转移时间下，飞行路径的长短也会存在差异，使得最终优化指标计算结果也随之变化。上述初始相位差尽管可在交会调相段加以修正，但因存在误差而造成远程导引前的相位差并非最佳。为进一步改善优化结果，以性能指标为参考基准搜索最佳转移时刻。实事上双星初始相对位置隐含了上述转移时刻的条件约束，通过离轨脉冲作用前调整追踪器的轨道位置来获得最佳转移时刻。为此，在优化模型中加入初始端点滑行过程，并将滑行时间作为优化设计变量之一。优化计算模型可表示为式（1）、式（2）和式（5）。式（1）给出了优化设计变量xn：

式中，Δt0为初始端滑行时间；Δti（i＝1，2，…，n－1）为相邻两脉冲转移时间；Δvj（j＝1，2，…，n－2）为惯性系下前n－2个脉冲矢量。与以往优化问题不同的是，脉冲数n也作为显示设计变量之一，因此式（1）中的设计变量个数为可变，对应的约束条件也是可变的。这里优化约束条件为

式中，i＝1，2，…，n－2，n≥2；Δvi为脉冲增量；Φ（rn，vn，tn）表示终端约束条件；Π（ui）为推力约束条件；P（Δt0，…，Δti，…，Δtn－1）是转移时间约束。函数f和g是追踪星轨道状态微分方程，如下：

式中，μ和req为引力常数和地球半径；控制变量ui＝Δvi；动力学方程（3）仅考虑了地球非球形摄动力J2项。在每步优化迭代过程中经数值积分获得追踪器和目标器惯性系下的位置和速度，如式（4）所示：

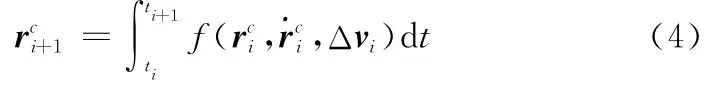
式中，ti＋1－ti＝Δti为相邻两脉冲间的转移时间，其初始值由遗传算法提供。转移时间将整个远程转移段分为了若干个间隔不等的区间，通过在其上积分获得ti时刻的，可得到最终末端时刻tf追踪星的位置和速度，并与目标星位置和速度比较获得优化修正量，同时转移时间亦作为显示优化变量。最后，优化设计变量数为4·（n－2）＋2，其中数字4对应了脉冲矢量vi和转移时间Δti二者的向量维数，n为脉冲数且为可变量，“＋”后的数字2对应为初始端的滑行时间和最后两脉冲的转移时间。优化性能指标为所有脉冲数增量的总和为

式中，最后两脉冲计算则由Lambert方法求解。

2 隐式遗传算法设计

2.1 隐式基因设计

遗传算法中每个样本个体都是由不同基因序列构成，这些基因由独立的设计变量经编码生成。通常基因长度依赖于设计变量个数，为保证在种群优化过程中的交叉等运算可行，设计变量个数必须固定。这种固定基因长度的遗传算法仅能处理设计变量数固定的优化问题。对于第1节中的多脉冲轨道交会问题则不再适用，需采用某种方法使得遗传算法中的样本基因具有某种长度可变特性。为此，通过在群体库中的每个样本添加数量不等的基因，使其所有样本基因数为可能的最大数，与各自样本中设计变量所对应的基因数的差值便是新增基因个数。如图1所示，其中深色部分表示有效基因，对应于实际优化变量；浅色部分表示隐式基因，这里的基因类型分组完全是基于个体基因参与适应度计算与否。

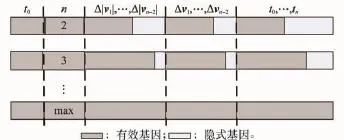
图1 含隐式基因的样本个体

2.2 编码设计

考虑到运算效率和精度，此次采用浮点数编码。把初始端滑行时间、脉冲的三轴分量和相邻脉冲间的转移时间作为编码变量。为了能处理条件约束以及提高遗传算法的搜索效率，对设计变量进行了归一化处理，即引入变量ρi和εi∈［0，1］（i＝1，2，…，n－1）按式（6）进行编码。

式中，变量ρi和εi在初始随机生成；Δvmax为最大允许速度增量；Tmax为整个转移时间上限。隐式基因编码与常规编码一致。

2.3 交叉变异运算

表1和表2给出了种群中脉冲数为4和5的两个任意样本个体，在相同序号位置对应的基因片段交叉运算过程示意，其中vi∈R4（i＝1，2，3）为惯性系下3个轴方向上的第i个脉冲矢量和点火时刻经实值编码后的单个基因。

表1 原始样本基因片

表1中4脉冲样本个体对应的脉冲矢量决策变量数为10，而5脉冲样本个体对应变量数则为14。首先定义x4∈R10和x5∈R14分别为4、5脉冲由式（1）所定义的决策向量，为了能对不同脉冲数进行寻优计算，需对4脉冲样本个体的基因排序号10以后引入隐式基因，即扩维使x′4∈R14。如表1中的、、和即为4脉冲个体样本中的隐式基因片，以浅色部分凸显标注。对于不同脉冲数n的样本个体均可通过引入隐式基因，使其达到最大nmax脉冲数对应维数4·（nmax－2）＋2。由于维数相同，使得不同脉冲数对应的样本个体可以如常规遗传算法进行种群交叉运算。

表2 交叉运算后样本基因片

假定交叉运算随机发生在样本个体序列v2所对应的位置。如表2所示脉冲数为4和5的基因片段从v2起止于v3发生了基因互换，这其中包含了隐式基因。表2给出了表1中样本个体x′4和x5经交叉运算后的新基因序列，这里交叉运算采用实值离散重组［14］，保证了脉冲数为n的基因排序号4·（n－2）＋2后的基因片段始终为隐式基因。对于变异过程则完全与常规遗传算法的交叉运算一致，如式（7）所示：

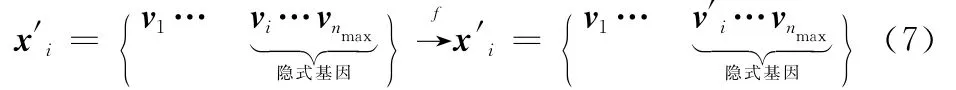
可见，引入隐式基因是为了保证种群中具有不同个数设计变量的样本在运算上可行，同时又可对上述含不同基因数的个体进行统一的数值寻优，进而一次获得期望的最优轨道转移解。更为重要的是这种含隐式基因的遗传算法在收敛性与传统遗传算法一致，有效地避免了多层迭代优化内外层相互影响而造成收敛性难以保证的问题。

2.4 适应度计算

根据式（5）给出的性能指标和式（2）中终端条件进行适应度函数设计，其计算公式如下：

式中，变量α、β满足α＋β＝1。

2.5 自适应调整

为避免早熟和增加种群多样性，借鉴文献［16］提出的自适应遗传算法，使得pc和pm的选取能随适应度函数式（8）自适应调整，其表达式为

式中，fmax为群体中最大适应度值；favg为每代群体的平均适应度值；f为个体当前适应度值。将式（9）中下标“c”换为“m”即为pm的计算式。

2.6 混合优化求解

由于式（2）中关于末端位置和速度等式约束在遗传算法中很难加以考虑，而且通过算法获得的时间域划分并非最优。加之遗传算法自身的概率特性使得单纯的遗传算法结果存在很大不确定性［14］。为此，需采用非线性寻优算法对其结果进一步优化。考虑到SQP是求解复杂非结性规划最有效的方法，而且当约束条件为凸时则优化结果逼近全局最优解［17］。本次混合优化计算采用SQP，其优化求解问题表述为

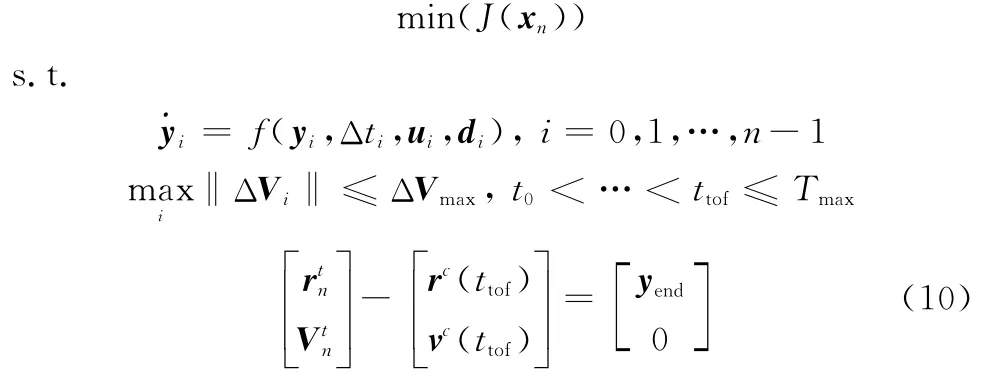
式中，J是式（5）给出的性能指标；xn为式（1）所定义的决策变量；yi是包含追踪星位置和速度的状态变量；f是轨道状态微分方程，这里远程导引段结束后的近程逼近段采用R－bar接近方式［1］。为此，变量yend为追踪器相对于目标器的轨道系下的距离，这里要求在目标星轨道系z轴方向上，即目标星质心与地心连线方向上要相距100 km。在末端速度上则要求与目标星一致。另外，因整个转移交会段被作用脉冲分成了若干子区间，脉冲作用时刻ti被作为显示优化变量。考虑因果关系ti＜ti＋1，需要对上述作用时刻优化变量t0，…，ti，…，tn附加如下约束：

由于转移段中的每一个子区域上的积分初始值是前一子区域的积分值，因此计算式（10）中追踪星末端值rc是一个串行积分形式

原始优化问题式（10）包含有强非线性约束，而SQP优化算法可通过将原始约束优化问题转化非约束问题，对迭代点xk处目标函数J的值域附近进行泰勒二阶项逼近，简化后的优化求解问题如式（14）所示，并满足相应KKT条件。

式中，dk为寻优方向，即为活性约束集合的零空间；Hk为上述转化后的非约束Lagrangian函数的Hessian矩阵，但计算时采用quasi-Newton方法对其逼近［17］，更新计算

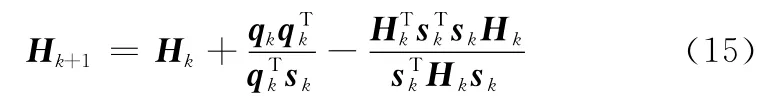
式中，变量qk和sk的求解表达式可参看文献［17］，而决策变量xk的更新计算公式为

式中，αk为更新步长，该优化迭代过程需要对初始决策变量x0进行合理赋值，否者将造成优化过程不可行［17］，本文采用遗传算法提供初值。最终，上述遗传混合优化算法流程如图2所示。

图2 含隐式基因的混合遗传算法流程

3 仿真计算及分析

3.1 仿真初始条件

首先给出两航天器初始轨道根数，如表3所示。

表3 双星轨道根数

表3中第1与第2行分别为追踪星和目标星在UTC时间2013年2月11日20时18分19.3秒时的开普勒轨道6要素，其中追踪星初始处在椭圆转移轨道上，目标星在地球同步轨道上。双星初始相位差为61.99°，目标星的轨道周期为86 176.04 s。

图3给出了双星在不同初始相位差，相同转移时间条件下，两脉冲速度增量变化，可知不同初始相位差对最终燃料消耗有较大影响。

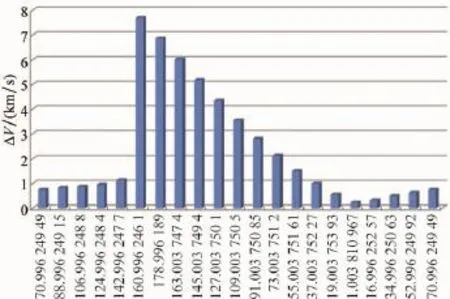
图3 不同初始相位角下的两脉冲幅值变化

表4给出了遗传算法参数的初始设置，并限定转移总时间小于目标轨道周期，另外在轨道机动中采用冲量理论及其相关假设［12］。

表4 遗传算法参数初始设置

这里假定了最大可能脉冲数为4，因在实际中过多的脉冲数反而会降低性能指标。

3.2 仿真结果

按照表4的参数设置，采用图2给出的算法流程，上述隐式基因混合遗传算法进行100次蒙特卡罗仿真，计算结果的均值如表5所示。

表5 3脉冲轨道转移计算结果

表5中的点火时刻是表3所定义的UTC相对时间。按照性能指标式（5）最终解算出3脉冲方式为最优轨道转移。速度增量总和为209.369 m／s，最后末端位置误差为1.208 km，速度误差为2.070 4 m／s，并满足式（10）给出的全部约束条件。表5中第1个脉冲进行推力加速接近远地点，在远地点附近进行轨道转移脉冲作用，最后一个脉冲则使追踪器沿着目标轨道飞行，并迫使满足末端位置和速度约束，即与目标星在轨道系中z轴方向上相距101.208 km。

图4给出群体适应度值随遗传代数变化的过程，表明群体中适应度值较小的个体依次被淘汰，较优个体则被保留并逐渐趋于最优值。

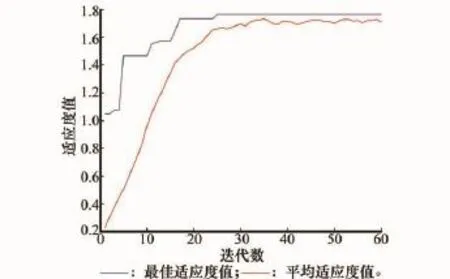
图4 适应度变化曲线

表6给出了不含隐式基因混合遗传算法分别针对2、3、4脉冲进行100次蒙特卡罗计算的均值结果，并与含隐式基因混合遗传算法得到的计算结果进行比较。

表6 不同脉冲数下的计算结果

从表6的计算结果可以看出，不同脉冲数下使用不含隐式基因的混合遗传算法获得的解基本一致，而且计算结果的方差较小。在满足转移总时间约束条件下，以燃料消耗和最终距离误差综合考虑，3脉冲下轨道转移是最优的，这与含隐式基因混合遗传算法的结果是一致的。

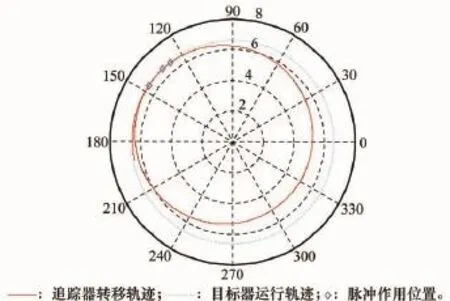
图5 轨道转移相平面示意图

从图5可清楚地看到，追踪器在椭圆转移轨道远地点进行的第2次脉冲点火用于轨道转移，之后的第3次脉冲用于调整末端位置和速度。上面轨道转移过程与霍曼转移非常相似，实际上针对表3给出的轨道参数，采用霍曼转移计算结果是192.597 m／s，然而本文研究的轨道交会与之又有所不同。这里需兼顾目标器末端位置、速度和转移时间，因此隐含了对最终交会时刻的约束，霍曼转移并不考虑末端时刻和转移时间约束，但是二者计算结果的相对偏差仅为8.7%。在不考虑时间约束的情况下，霍曼转移是共面轨道转移的最优解［19］，可见本文给出的计算结果非常接近最优解，下面将进一步采用主矢量判据进行计算结果的最优性分析。

3.3 最优判据及主矢量计算

主矢量p定义为关于速度的协态变量，即p≡λv。可将原始脉冲最优控制的必要条件转为对主矢量的4个条件约束［2］：①主矢量及其一阶导数连续；②脉冲作用时刻，主矢量与脉冲反向幅值为1；③主矢量幅值不大于1是多脉冲最优的必要条件；④脉冲作用时刻，端点除外的主矢量幅值导数为零。主矢量通过式（17）计算：

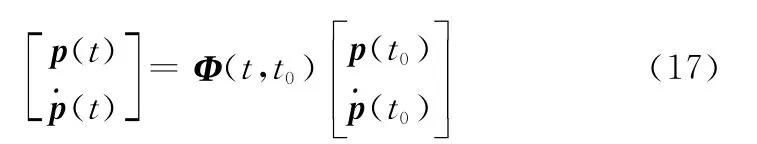
式中，Φ（t，t0）为状态转移矩阵，其形式为

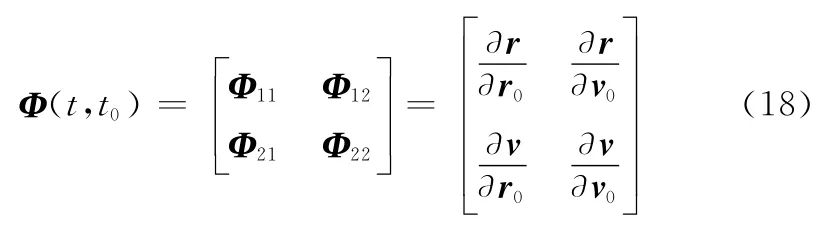
依据文献［18］，4个子矩阵Φ11、Φ12、Φ21和Φ22可有如下表示：

采用式（19）给出的状态转移矩阵可处理远距离椭圆轨道的状态外推，而主矢量计算如下：

基于前面对主矢量的最优条件和计算公式（20），可作为对本文算法结果的最优性评估的判据，进而验证本文算法的最优性。

按照式（17）～式（20）进行轨道转移过程的主矢量计算，其结果如图6所示。结合表5的仿真结果和3.3节中最优控制判据，可知在脉冲点火时刻主矢量p接近1，而在其他时刻主矢量幅值均不大于1，且主矢量及其一阶导数连续，因此表5给出的仿真结果满足最优控制必要条件。再结合前面与霍曼转移结果的比较，可知本文给出的算法计算结果无限接近全局最优解。

图6 轨道转移过程主矢量变化值

最后对3脉冲下初始端有、无滑行的100次蒙特卡罗仿真均值结果进行比较，如表7所示。

表7 初始端有无滑行结果对比

可见加入初始端滑行后，对性能指标有一定改善，另外不同初始相位差改善程度也有差别。

4 结论

通过向种群中的样本个体添加隐式基因，使得遗传算法具有了某种基因长度可变的特性，本质上是扩大了数值寻优的集合空间，丰富了个体的差异性。在算法结构上仅为单层迭代，使得在收敛性上与传统遗传算法一致。基于该隐式基因遗传算法可同时解出脉冲个数和脉冲矢量等优化变量，而且对整个转移时间区间进行了合理的划分。最后，通过采用SQP对遗传算法的计算结果进一步寻优，进而保证了结果的确定性和最优性。通过比较有等待和无等待阶段性能指标值，可知合理地在航天器交会策略中添加等待滑行段可以消耗更少的能量而实现轨道交会。本文尽管仅针对某一特定的初始相位差进行轨道转移，但因加入了初始端滑行来调整双星相位差，故该方法可以推广到任意初始相位差的共面椭圆轨道转移。

最后基于数值计算结果表明：含隐式基因的混合遗传算法能够很好地处理各种约束条件下的优化问题，特别是针对设计变量个数可变的复杂寻优计算，而以往常规遗传算法对此问题则很难获得求解。基于主矢量和霍曼转移计算值可知所获得的结果是无限逼近于全局最优解。

［1］Wigbert F.Automated rendezvous and docking of spacecraft［M］.New York：Cambridge University Press，2003：17- 19.

［2］Conway B A，Prussing J E，Kluever C A，et al.Spacecraft trajectory optimization［M］.New York：Cambridge University Press，2010：3- 4.

［3］Betts J T.Practical methods for optimal control and estimation using nonlinear programming［M］.New York：SIAM Press，2010：123- 217.

［4］Santos D，Prado A，Colasurdo G.Four-impulsive rendezvous maneuvers for spacecrafts in circular orbits using genetic algorithms［J］.Mathematical Problems in Engineering，2012，19（2）：94- 113.

［5］Reichert A K.Using a genetic algorithm to determine the optimum two-impulse transfer between co-planar，elliptical orbits［C］∥Proc. of the AAS Rocky Mountain Guidance Conference，2004：111- 135.

［6］Rauwolf G A.Near-optimal low-thrust orbit transfers generated by a genetic algorithm［J］.Journal of Spacecraft and Rockets，1996，33（6）：859- 862.

［7］Huang Y，Li X J，Zhang D L，et al.Application of hybrid genetic algorithm in optimal Lambert orbital transfer design［J］.Flight Dynamics，2013，31（3）：269- 272.（黄勇，李小将，张东来，等.混合遗传算法在最优Lambert轨道转移设计中的应用［J］.飞行力学，2013，31（3）：269- 272.）

［8］Ossama A.N-impulse orbit transfer using genetic algorithms［J］.Journal of Spacecraft and Rockets，2007，44（2）：456- 459.

［9］Luo Y Z，Zhang J，Li H Y，et al.Interactive optimization approach for optimal impulsive rendezvous using primer vector and evolutionary algorithms［J］.Acta Astronautica，2010，67（2）：396- 405.

［10］Alessandro Z，Guido C.Indirect optimization of finite-thrust cooperative rendezvous［J］.Journal of Guidance，Control，and Dynamics，2015，38（2）：456- 459.

［11］Ahmed G，Abdelkhalik O.Hidden genes genetic algorithm for multi-gravity-assist trajectories optimization［J］.Journal of Spacecraft and Rockets，2011，48（4）：629- 641.

［12］Tang G J，Luo Y Z，Yong E M.Spacecraft trajectory optimization theory，methods and applications［M］.Beijing：Science Press，2011：167- 227.（唐国金，罗亚中，雍恩米.航天器轨迹优化理论、方法及应用［M］.北京：科学出版社，2011：167- 227.）

［13］Vallado D A.Fundamentalsof astrodynamics and applications［M］.3rd ed.New York：Microscom Press，2007：319- 412.

［14］Wang X P，Cao L M.Genetic algorithm—theory，application and software implementation［M］.Xi’an：Xi’an University Press，2002：12- 34.（王小平，曹立明.遗传算法—理论、应用与软件实现［M］.西安：西安交通大学出版社，2002：12- 34.）

［15］Oliver M，Eberhard G.Satellite orbits-models，methods and applications［M］.Berlin Heidelberg：Spring Verlag Press，2000：53- 154.

［16］Srinivas M，Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithm［J］.IEEE Trans.on Systems，Man and Cybernetics，1994，24（4）：656- 666.

［17］Jorge N，Stephen J W.Numerical optimization［M］.2nd ed.New York：Spring Press，2006：448- 492.

［18］Der G.J.An elegant state transition matrix［J］.Journal of the Astronautical Sciences，1997，45（4）：371- 390.

［19］Prussing J E，Conway B A.Orbital Mechanics［M］.New York：Oxford University Press，1993：12- 23.

Hidden hybrid genes genetic algorithm for multi-impulse rendezvous maneuvering

OUYANG Gao-xiang1，WANG Xiao-li2，SUN Cheng-ming1，YANG Xin1
（1.Academy of Opto-Electronics，Chinese Academy of Sciences，Beijing 100094，China；2.Beijing Institute of Control Engineering，Beijing 100090，China）

The spacecraft rendezvous problem of transferring between two coplanar elliptical orbits with free time is studied，which looks for multi-impulsive transfer at the expense of fuel optimization under lots of constraints.Different number of pulses will change the number of variables to solve optimization problems.Through the introduction of hidden genes in the genetic algorithm，the individuals in the gene groups have a variable-length feature.The optimal solution to the number of pulses and impulse vectors is obtained at the same time.In order to further improve the optimal solution，an initial coast is introduced to be as an optimal variable，which results in the just pulse moment of de-orbit for chaser.Firstly，a genetic algorithm is applied to find initial guess values，and then the sequential quadratic programming（SQP）algorithm is used to iteratively improve the above non-optimal solution and converge to a global optimal transferring.Finally，on the base of the primer vector theory and control optimal criterion，it indicates that the hidden genes hybrid genetic algorithm can serve as an effective optimization method to solve effectively a class of complex problems，in addition the multi-pulse rendezvous guidance law design which includes variable number of variables optimized also can successfully be done.

multi-pulse；coplanar elliptical orbits；hidden genes；hybrid genetic algorithm；sequential quadratic programming（SQP）；primer vector

V 412.4

10.3969／j.issn.1001-506X.2015.12.22

欧阳高翔（197-7- ），男，高级工程师，博士，主要研究方向为飞行器设计。

E-mail：oygx210＠163.com

王小丽（198-3- ），女，工程师，硕士，主要研究方向为航天器鲁棒控制。

E-mail：shalyli＠126.com

孙成明（198-4- ），男，副研究员，博士，主要研究方向为空间目标光学探测与识别。

E-mail：sunchengming2008＠163.com

杨新（1967- ），男，研究员，博士，主要研究方向为飞行器设计。

E-mail：yangxin＠aoe.ac.cn

1001-506X（2015）12-2810-07