无人机任务分配与航迹规划协同控制方法

2015-06-05孙小雷齐乃明姚蔚然

系统工程与电子技术 2015年12期

关键词：航程多边形航迹

孙小雷，齐乃明，董程，姚蔚然

（1.哈尔滨工业大学航天学院，黑龙江哈尔滨150001；2.北京航天新风机械设备有限责任公司，北京100854）

无人机任务分配与航迹规划协同控制方法

孙小雷1，齐乃明1，董程2，姚蔚然1

（1.哈尔滨工业大学航天学院，黑龙江哈尔滨150001；2.北京航天新风机械设备有限责任公司，北京100854）

针对无人机协同控制问题，提出一种多无人机任务分配与航迹规划的整体控制架构。将威胁和障碍区域考虑为合理的多边形模型，使用改进的A*算法规划出两个航迹点之间的最短路径。并利用该路径航程作为任务分配过程全局目标函数的输入，采用与协同系统相匹配的粒子结构进行改进粒子群优化（particle swarm optimization，PSO）任务分配迭代寻优。根据分配结果并考虑无人机性能约束，基于B-spline法平滑路径组合，生成飞行航迹。仿真结果表明，算法在保证计算速度和收敛性能的同时，能够产生合理的任务分配结果和无人机的可飞行航迹。

无人机；任务分配；航迹规划；改进A*算法；改进粒子群优化

0 引言

无人机在民用领域和军事战略中起着越来越重要的作用，能够完成包括火灾监测、搜索救援、侦查追踪和执行歼灭等多种任务［1-3］。执行任务的复杂性以及环境的不确定性，要求无人机系统具有更高的决策能力和自主性。

而任务分配和航迹规划是多无人机实现协同自主控制的关键技术［4］。由于任务分配与航迹规划属于非确定性多项式（nondeterministic polynomial，NP）问题［56］，穷举法或最优控制法求解过程将耗费大量的计算代价，甚至难以实现。所以该领域在近_些年的研究中主要以智能算法为核心［7-9］，求取近似最优结果，主要包括：模拟退火（simulated annealing，SA）算法、进化算法（evolution algorithm，EA）、遗传算法（genetic algorithm，GA）和粒子群优化（particle swarm optimization，PSO）算法等。任务分配算法应以航迹航程建立全局目标函数，目前的研究过程中一般假设航程已知，或用直线距离近似航程，使得算法应用具有很大的局限性。

故本文提出一种无人机任务分配与航迹规划整体控制架构，首先采用改进A*算法并考虑多边形障碍区域［10］计算无人机与任务点间的最短路径；基于该最短路径航程，使用改进PSO算法计算任务分配方案；最后利用B-spline法离散化无人机承担任务的组合路径，生成可飞行航迹。

1 协同控制架构

多无人机协同控制架构包括任务规划系统与航迹规划系统，如图1所示。任务规划系统基于场景中无人机与任务信息改进PSO粒子结构，以航迹规划系统计算的最短路径航程建立全局目标函数的自变量信息，计算任务分配结果，求得每架无人机所承担的任务组合及执行顺序。

图1 任务与航迹规划协同控制架构

航迹规划系统包括以改进A*算法为核心的路径规划算法及基于B-spline法的航迹平滑算法两部分。路径规划采用改进A*算法计算无人机与任务点间的最短路径，将直接可到达多边形顶点作为改进A*算法的备选节点，提高算法计算效率；航迹平滑算法以B-spline法为核心，考虑无人机自身性能约束对每架无人机的路径段组合进行平滑计算，得出无人机可飞行航迹。

2 基于改进PSO的任务分配算法

2.1 任务描述

假设无人机协同控制应用场景包含N架无人机和M个待执行任务，则任务分配矩阵sij为

式中，i∈I，j∈J；I＝｛1，2，…，N｝与J＝｛1，2，…，M｝分别为无人机与任务索引集合。

任务分配的目标是最大化全局目标函数，实现任务到无人机的无冲突分配，无冲突指每个任务只能由一架无人机来执行，但每架无人机可根据自身能力执行多个任务。

根据上述信息，全局目标函数［11］建立为

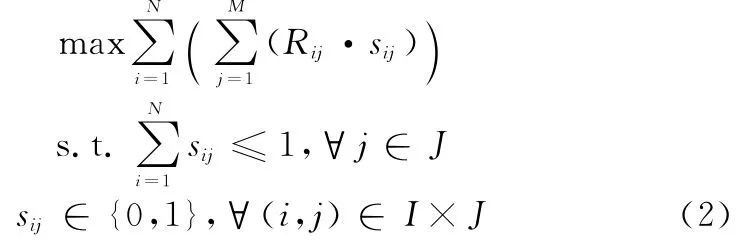
式中，Rij为无人机i分配到任务j后的奖赏函数，一般与对应的航迹航程相关。

2.2 任务奖赏函数

无人机i分配到任务j后所得的得分值Rij为任务奖励函数与惩罚函数之和［12］。奖励函数Rewj具备任务时效性，惩罚函数Costij为燃料相关函数

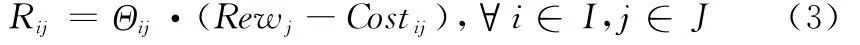
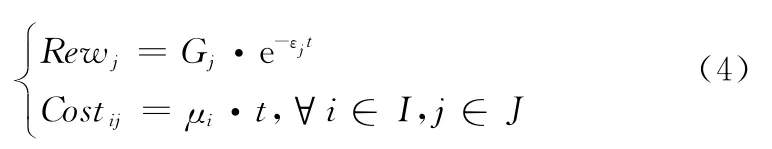
式中，t为执行时间；Gj为任务j的静态得分值；εj和μi为相关权重常数。Θij＝ηi ijξj为约束因数，其中ηi为燃料约束，表示剩余燃料可飞行航程Dr（i）应大于航迹航程Di；ζij为任务匹配约束；ξj为任务有效期约束，任务j开始时间pj与结束时间qj，满足如下关系：

2.3 改进PSO任务分配

设PSO算法的种群规模为Q，根据任务分配场景信息，考虑到N架无人机执行M个任务，PSO的粒子位置向量dn构建为

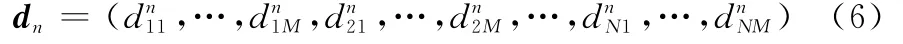
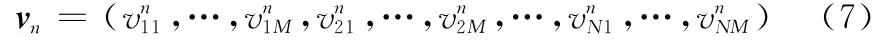
设最佳粒子位置为pn，种群最优位置为pg，第k次粒子更新公式为

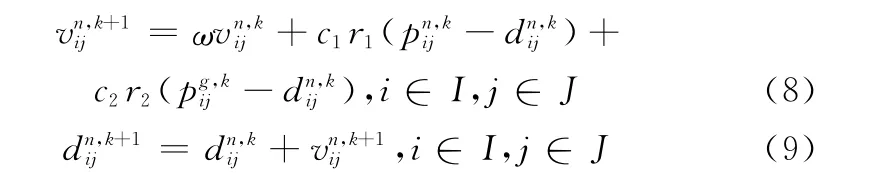
式中，ω为惯性常数；c1，c2为加速度系数；r1，r2为［0，1］上均匀分布的随机数。

下面给出改进PSO算法步骤。外循环（第2～12行）不断更新直至满足算法终止条件，其中内循环（第3～11行）为每个粒子更新过程。

3 航迹规划系统

3.1 无人机质心运动方程

在执行任务中无人机短时间内一般保持同一高度飞行，其二维质心运动方程［13］为

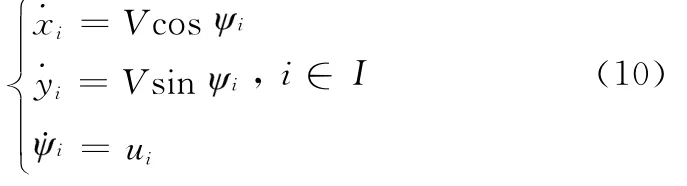
式中，（xi，yi）为无人机i的二维坐标；V表示飞行速度；i为航向角；ui为对应的控制量，最小转弯半径rmin＝V／ui。控制量与航向角约束为

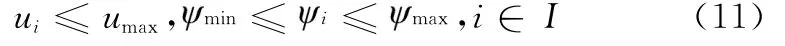
3.2 基于改进A*算法的路径规划算法

最短路径可以定义为，连接无人机与任务点且不穿过多边形威胁区域的最短组合折线长度。为简化问题，做如下假设：

（1）只考虑无人机的质心运动方程；

（2）障碍物及威胁可用多边形近似；

（3）无人机具备防碰撞能力及控制算法。

A*算法为经典启发式算法［1415］，计算当前位置可到达路径点距离，选择最小距离路径点列入备选路径点集合。路径点d的距离函数为

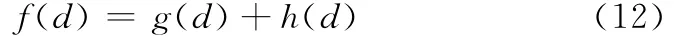
式中，g（d）表示起点到当前路径点d的真实距离；h（d）表示路径点d到目标点的估计距离。

取代了标准A*算法的搜索区域，本文提出的改进A*算法用当前位置可直接到达的多边形威胁区顶点作为备选路径点，以减少了算法的计算次数，该阶段只考虑最短路径，航迹平滑阶段将加入安全距离及无人机自身性能等约束。如图2所示，扇形O1OO2区域为无人机已估算范围，P1、P2与P3为障碍区域，初始路径点O的下一阶段备选路径点为｛A，A1，A2，A3｝，路径点A的备选路径点为｛B，B1｝，以此类推。

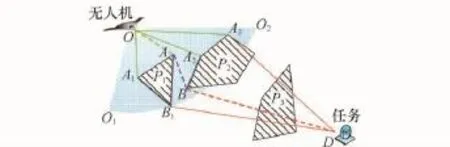
图2 改进A*算法备选路径点选择

图3描述了改进A*算法最优路径计算过程。在已估算范围内，考虑障碍规避规划出无人机与任务间的最短折线路径g（d），即OA＋AB。在估算范围外，用无人机与任务的直线距离，即线段BD的加权来近似障碍规避后的实际路径BC＋CD，得到估计航程h（d），从而得到改进A*算法的距离函数f（d）。

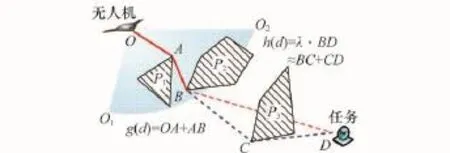
图3 改进A*算法最优路径求取过程

改进A*最优路径算法可减少不必要的计算量，具体计算流程如下：——

图4给出一种应用场景的仿真结果，多边形为障碍外形。虚线段即为该算法求取的最优路径，可以看出在未考虑安全距离等因素下，改进A*算法可有效规划出一条无人机与任务间的最短路径。

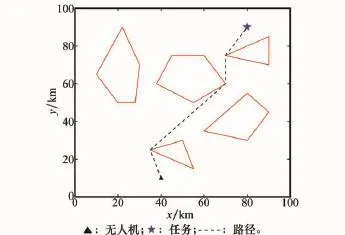
图4 最优路径求取结果

3.3 基于B-spline的航迹平滑算法

航迹平滑阶段除无人机自身性能约束外，还需考虑飞行安全距离等约束，可通过在B-spline法中添加控制点的方式来实现。特别是在多边形威胁区域顶点处，在二维空间中可通过设置两个控制点能够有效规避威胁并生成平滑飞行航迹。二维B-spline离散化曲线方程［16］定义为

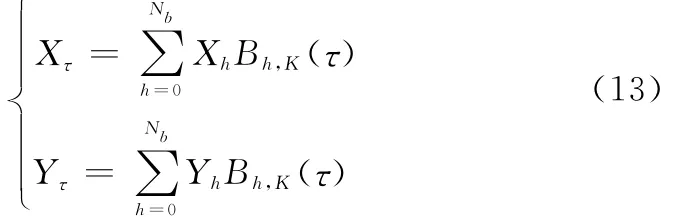
式中，（Xh，Yh）（h＝0，…，Nb）为求得的控制点；Bh，K（τ）为K阶基函数，更新方程如下：

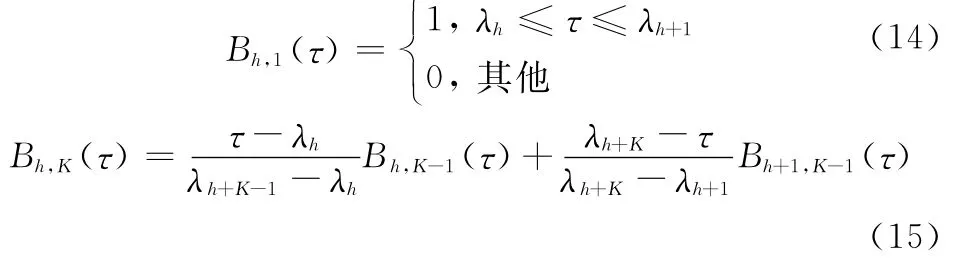
其中，节点方程为

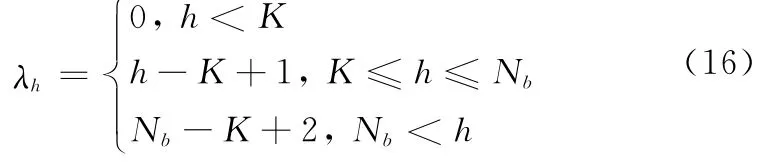
4 仿真实验分析

仿真实验中随机给出4个无人机及7个任务位置，并设置任务奖赏函数。以Core E5800 3.2 GHz CPU，4 G内存的Dell PC为仿真实验环境。假设无人机恒速飞行，速度为200 m／s，最小转弯半径2 km，控制量约束umax＝6°／s，障碍规避安全距离4 km。

图5给出该条件下的仿真实验结果，其中多边形为障碍区域。以无人机1为例，虚线段为航迹平滑前使用改进A*算法产生的最短路径。改进PSO算法任务分配后无人机1承担任务1和任务3，并给出路径组合，实线为采用B-spline法生成的可飞行航迹。可以看出为了有效规避威胁，航迹附近每个多边形威胁区的顶点处设置两个控制点，并得到了较理想的航迹规划结果。

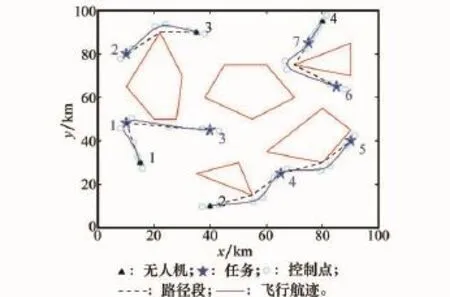
图5 协同控制系统仿真结果

图6为任务场景中控制量随时间的变化规律。可以看出每架无人机的控制规律不仅与仿真场景中的对应曲线相一致，并且控制曲线连续平滑，控制规律较易实现。

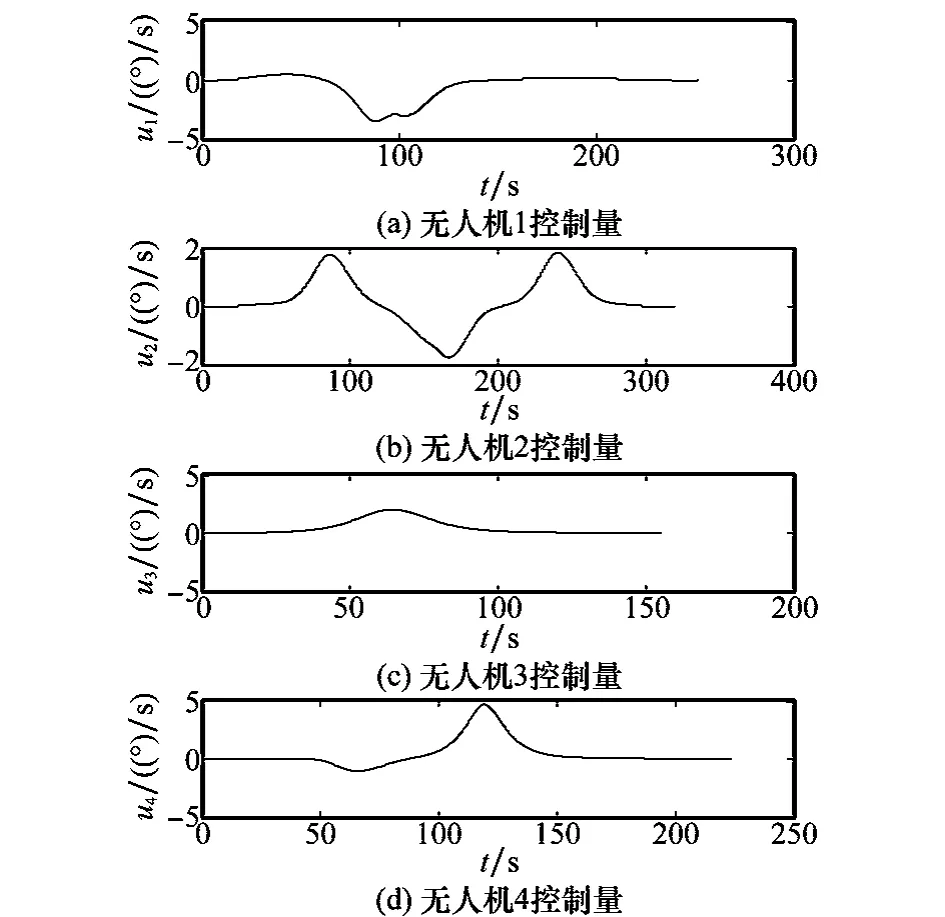
图6 仿真场景中无人机控制量

5 结论

本文提出一种无人机协同控制系统架构，包括任务规划及航迹规划子系统。航迹规划系统使用改进A*算法规划出最短路径，提供任务规划系统的控制输入，使其完成任务分配过程。任务规划系统基于无人机应用场景相关的改进PSO算法，求解任务分配结果，反馈至航迹规划系统，利用B-spline法生成无人机可飞行航迹。仿真结果验证了算法的有效性，并给出了仿真场景中每架无人机的控制量。

［1］Kalyanam K，Chandler P，Pachter M，et al.Optimization of perimeter patrol operations using unmanned aerial vehicles［J］.Journal of Guidance，Control，and Dynamics，2012，35（2）：434- 441.

［2］Shaferman V，Shima T.Unmanned aerial vehicles cooperative tracking of moving ground target in urban environments［J］.Journal of Guidance，Control，and Dynamics，2008，31（5）：1360- 1371.

［3］Bethke B，Valenti M，How J P.UAV task assignment［J］.IEEE Robotics and Automation Magazine，2008，15（1）：39- 44.

［4］Chen Z J，Wei J Z，Wang Y X，et al.UAV autonomous control levels and system structure［J］.Acta Aeronautica et Astronautica Sinica，2011，32（6）：1075- 1083.（陈宗基，魏金钟，王英勋，等.无人机自主控制等级及其系统结构研究［J］.航空学报，2011，32（6）：1075- 1083.）

［5］Shen L C，Chen J，Wang N.Overview of air vehicle mission planning techniques［J］.Acta Aeronautica et Astronautica Sinica，2014，35（3）：593- 606.（沈林成，陈璟，王楠.飞行器任务规划技术综述［J］.航空学报，2014，35（3）：593- 606.）

［6］Bertuccelli L F.Robust decision-making with model uncertaintyin aerospace systems［D］.Cambridge：Massachusetts Institute of Technology，2008.

［7］Ni T Q，Wang J D，Liu Y A.Application of particle swarm algorithm in route planning of UAV［J］.Systems Engineering and Electronics，2011，33（4）：806- 810.（倪天权，王建东，刘以安.交叉粒群算法在无人机航路规划中的应用［J］.系统工程与电子技术，2011，33（4）：806- 810.）

［8］Mc Lain T W，Beard R W.Coordination variables，coordination functions，and cooperative timing missions［J］.Journal of Guidance，Control，and Dynamics，2005，28（1）：150- 161.

［9］Sahingoz O K.Generation of Bezier curve-based flyable trajectories for multi-UAV systems with parallel genetic algorithm［J］.Journal of Intelligent and Robotic Systems，2014，74（1／2）：499- 511.

［10］Koyuncu E，Ure N K，Inalhan G.Integration of path／maneuver planning in complex environments for agile maneuvering UCAVs［J］.Journal of Intelligent&Robotic Systems，2010，57（1／4）：143- 170.

［11］Shen L C，Niu Y F，Zhu H Y.Theories and methods of autonomous cooperative control for multiple UAVs［M］.Beijing：National Defense Industry Press，2013：82- 85.（沈林成，牛轶峰，朱华勇.多无人机自主协同控制理论与方法［M］.北京：国防工业出版社，2013：82- 85.）

［12］Bakker T，Klenke R H.Dynamic multi-task allocation for collaborative unmanned aircraft systems［C］∥Proc.of the 52nd Aerospace Sciences Meeting，2014：1- 10.

［13］Wan M，Dai Z，Chu W K.Turning path planning for UAV in region coverage with scanline［J］.Systems Engineering and Electronics，2014，36（9）：1750- 1754.（万明，代忠，褚文奎.无人机扫描线区域覆盖中的转弯航迹规划［J］.系统工程与电子技术，2014，36（9）：1750- 1754.）

［14］Chandler P R，Rasmussen S，Pachter M.UAV cooperative path planning［C］∥Proc.of the AIAA Guidance，Navigation，and Control Conference and Exhibit，2000：1- 11.

［15］Jia Q X，Chen G，Sun H X，et al.Path planning for space manipulator to avoid obstacle based on A*algorithm［J］.Journal of Mechanical Engineering，2010，46（13）：109- 115.（贾庆轩，陈钢，孙汉旭，等.基于A*算法的空间机械臂避障路径规划［J］.机械工程学报，2010，46（13）：109- 115.）

［16］Nikolos I K，Valavanis K P，Tsourveloudis N C，et al.Evolutionary algorithm based offline／online path planner for UAV navigation［J］.IEEE Trans.on Systems Man and Cybernetics Part B，2003，33（6）：898- 912.

Cooperative control algorithm of task assignment and path planning for multiple UAVs

SUN Xiao-lei1，QI Nai-ming1，DONG Cheng2，YAO Wei-ran1
（1.School of Astronautics，Harbin Institute of Technology，Harbin 150001，China；2.Beijing Aerospace Xinfeng Machinery Equipment Limited Liability Company，Beijing 100854，China）

An integrating framework of task assignment and path planning for multiple unmanned aerial vehicles（UAVs）is presented.To avoid the obstacles area which is represented as polygon，the shortest path segment between UAVs and task can be found by the improved A*algorithm.According to this segment distance，the global objective function of task allocation is modeled.The assignment process is determined by improved particle swarm optimization（PSO），which particle structure matches the cooperative system.The B-spline method is adopted to smooth the flight path，which consists of path segments of the assignment.Numerical results demonstrate that the proposed method can achieve the optimal task assignment solution and best flight routes.

unmanned aerial vehicle；task assignment；path planning；improved A*algorithm；improved particle swarm optimization（PSO）

V 19

10.3969／j.issn.1001-506X.2015.12.17

孙小雷（198-5- ），男，博士研究生，主要研究方向为飞行器协同任务分配与航迹规划方法。

E-mail：yuyancool＠163.com

齐乃明（1962-- ），男，教授，博士，主要研究方向为飞行器机电一体化。

E-mail：qnmok2000＠163.com

董程（198-3- ），男，副主任工艺师，主要研究方向为飞行器机电一体化。

E-mail：dongo2001＠163.com

姚蔚然（199-0- ），男，硕士研究生，主要研究方向为飞行器协同智能控制与优化算法。

E-mail：yaowr1990＠163.com

1001-506X（2015）12-2772-05