基于改进DPC近似的多子阵SAS距离多普勒算法

2015-06-05唐劲松钟何平

系统工程与电子技术 2015年12期

关键词：合成孔径声呐历程

田振，唐劲松，张森，钟何平

（海军工程大学海军水声技术研究所，湖北武汉430033）

基于改进DPC近似的多子阵SAS距离多普勒算法

田振，唐劲松，张森，钟何平

（海军工程大学海军水声技术研究所，湖北武汉430033）

传统修正的偏置相位中心近似方法往往忽略距离历程近似误差的方位空变性，使得基于该方法的成像算法重建的图像出现近距离散焦和方位向偏移现象。为解决该问题，该文对修正的偏置相位中心近似方法进行改进，将双根号形式距离历程表示为类收发合置项、距离空变项和方位空变项之和的形式，有效提高了距离历程的近似精度；在利用驻定相位原理求取方位向驻定相位点的过程中，通过充分考虑距离历程方位空变性的影响，推导了更为精确的方位向驻定相位点，有效提高了点目标响应二维谱的准确性。在此基础上，提出一种适用于高分辨多子阵合成孔径声呐成像的距离多普勒算法，仿真试验和实测数据成像结果验证了该算法的有效性。

多子阵合成孔径声呐；距离多普勒算法；偏置相位中心近似；方位空变

0 引言

由于水声传播的低速性，传统的单阵合成孔径声呐（synthetic aperture sonar，SAS）很难同时兼顾高的方位向分辨率和高的测绘速率，多子阵技术［14］的引入很好地解决了这一问题，但是也增加了成像算法的复杂性。多子阵技术导致点目标回波响应的距离历程不再是单一的双曲函数，而是两个根式之和，这使得难以利用传统的驻定相位原理［5］推导严格解析的点目标二维谱，从而难以推导出快速有效的高分辨多子阵SAS成像算法。另外，多子阵SAS系统的拖曳速度与水下声速可比拟，适用于合成孔径雷达［67］（synthetic aperture radar，SAR）的停走停近似不再成立，必须考虑信号发收期间SAS平台运动引入的方位向走动，这种停走停近似不成立的情况称为非停走停模式［8］。

为了推导解析的点目标二维谱，最直接的方法是对双根号形式的距离历程进行近似。文献［9］提出了经典的偏置相位中心（displacement phase center，DPC）近似方法，该近似认为发射阵和接收阵之间存在一个虚拟的阵元，声呐从该阵元相位中心发射并接收信号。该近似具有广泛的适用性，但是误差较大。文献［10］提出了一种改进的DPC近似方法，该方法部分考虑了DPC近似带来的误差，但是没有考虑非停走停模式引入的方位向走动。文献［11］继续对DPC近似进行改进，提出了一种停走停近似修正的DPC近似方法。但是该方法对于DPC近似误差的修正只考虑了距离空变，没有考虑方位空变，近距误差较大。文献［12］对于DPC近似误差的修正虽然考虑了方位空变，但是在利用驻定相位原理求取方位向驻定相位点时忽略了方位空变的影响，导致点目标响应二维谱不够精确，导致成像质量下降。

本文提出一种适用于多子阵SAS高分辨成像的距离多普勒（range Doppler，RD）算法，该算法在基于非停走停模式，将双根号形式的距离历程表示为类收发合置项、距离空变项和方位空变项之和的形式，大大降低了距离历程近似引入的误差。在求取方位向驻定相位点时，本文充分考虑了距离历程近似中方位空变的影响，推导了更加精确的驻定相位点和点目标响应二维谱，有效提高了成像算法的精度。仿真试验和湖试结果验证了所提算法的有效性。

1 多子阵SAS距离历程几何模型

多子阵SAS距离历程几何模型如图1所示，SAS沿X轴（方位向）以速度v作匀速直线运动，发射阵在前，接收阵在后，点目标位于（0，r）处。在t时刻，发射阵向正侧方向以恒定的脉冲重复间隔发射线性调频信号，设其坐标为（vt，0），用RT（t；r）表示此时发射阵与点目标之间的距离。假设在t＋时刻，接收阵i接收到来自目标的反射回波，用RRi（t；r）表示此时接收阵i与点目标之间的距离，表示信号发收过程花费的时间，即＝［RT（t；r）＋RRi（t；r）］／c，c表示水下声速。Δdi表示发射阵与接收阵i等效相位中心之间的间隔，即Δdi＝（i－1）D，D为相邻子阵等效相位中心之间的间隔。因此，接收阵i的坐标可以表示为（vt－Δdi＋，0）。

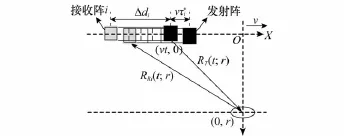
图1 多子阵SAS距离历程几何模型

用Ri（t；r）表示信号发收期间总的距离历程，那么有

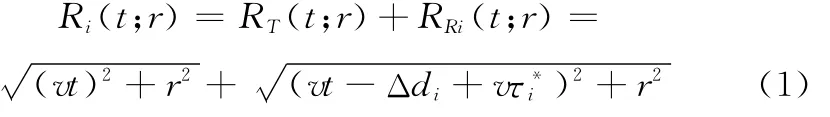
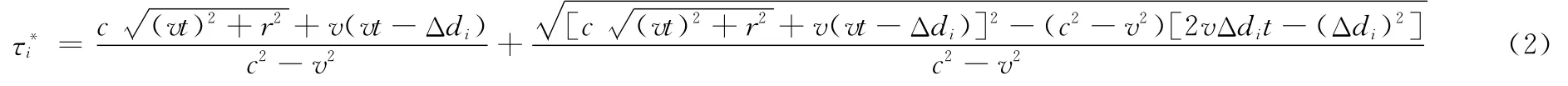
显然，式（2）相当复杂，很难被直接利用于快速的多子阵SAS成像算法推导，当波束较窄时，通常用2r／c近似代替。需要注意的是，当目标距离较近时，该近似也可应用于宽波束的情形。

与双基地SAR相类似［15］，式（1）是典型的双根号形式，这将导致很难利用传统的驻定相位原理获取精确的点目标二维谱。为了解决这个问题，该文对双根号形式的距离历程进行近似处理，即

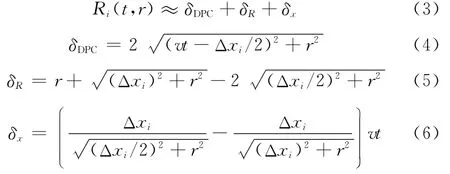
式中，Δxi＝Δdi－v·2r／c表示不同接收阵和非停走停模式引入的收发分置畸变项，当Δxi＝0时，式（3）退化为单阵收发合置的形式。

当Δxi≠0时，δDPC与收发合置形式相类似，被称为类收发合置项；δR为DPC近似误差的距离空变项，文献［11］中关于DPC近似误差仅为δR对Δxi进行泰勒近似且保留二阶项的情形，是本文近似的特殊情况；δx为DPC近似误差的方位空变项，此处仅考虑方位空变的一阶线性变化特性。

距离历程近似通常会引入一定的相位误差，当误差较大时会导致图像质量下降，当相位误差小于π／8时，该部分误差才可以忽略。为了验证本文近似能否满足要求，对式（3）引入的相位误差进行仿真分析，仿真参数如下：信号载频为150 k Hz，信号带宽为20 k Hz，SAS平台航速为3.2 m／s，接收阵个数为48个，接收阵长度为8 cm，距离向采样距离为40～410 m。为了确保误差分析过程中真实距离历程不存在误差，不进行任何近似，直接采用式（2）的精确表达式。

误差分析结果如图2所示，其中图2（a）为修正的DPC近似［11］引入的相位误差，图2（b）为本文近似引入的相位误差，图2（c）为两种近似引入的最大相位误差随距离的变化情况。由图2（a）和图2（b）可知，两种近似方法在近距离处误差较大且为负值，随着距离的增大，误差变为正值并逐渐增大。相位误差一般考查其绝对值，因此图2（c）中的相位误差均是指误差的绝对值。如图2（c）所示，当目标距离小于62.58 m时，修正的DPC近似引入的相位误差将超过临界值π／8，当目标距离为40 m时，相位误差达到0.292 1π，超过临界值，不能满足近距离点目标的成像要求。相比之下，当目标距离为40 m时，本文近似引入的相位误差仅为0.104 0π，仍然小于临界值，远远优于修正的DPC近似。

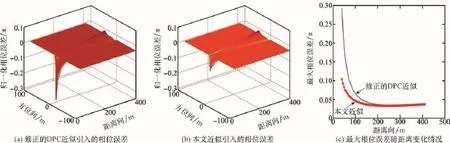
图2 误差分析

2 多子阵SAS RD算法推导

2.1 单个子阵点目标响应二维谱

严格解析的点目标响应二维谱是推导快速的高分辨多子阵SAS成像算法的关键。多子阵SAS系统通常由单个发射阵向正侧方向发射线性调频信号，多个接收阵共同接收来自目标的反射回波。以接收阵i为例，经过解调至基带，接收阵i接收到的点目标回波响应可以表示为

式中，A为信号幅度；τ为距离快时间；f0为信号中心频率；ωa（·）由收发系统基阵的方向性函数决定；p（·）为线性调频脉冲，p（τ）＝rect（τ／Tr）·exp（jπkτ2），Tr为脉冲宽度；k为调频斜率。如无特别说明，后续推导中忽略与成像质量无关的幅度项。

将式（7）沿距离向作傅里叶变换（Fourier transform，FT），可得

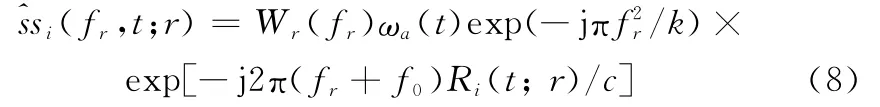
式中，fr表示距离向基带频率；Wr（·）表示距离向频谱的包络形状。

将式（3）代入式（8），并将回波响应沿方位向作FT进入二维频域，有

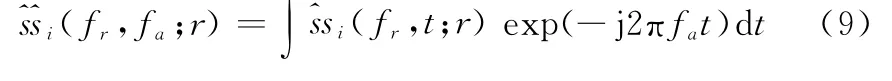
式中，fa表示方位向频率。

依据驻定相位原理，方位向驻定相位点可以表示为

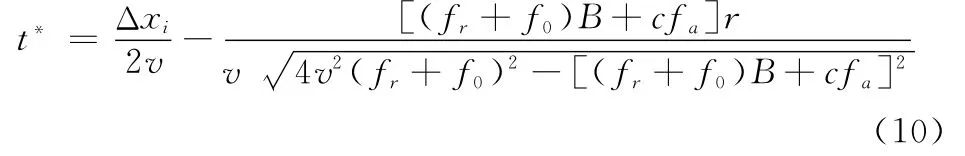
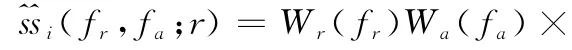
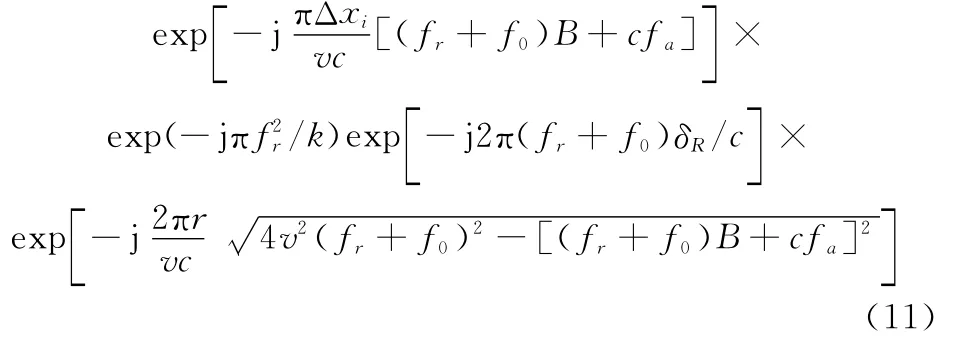
式中，Wa（·）表示方位向频谱包络形状。不妨令

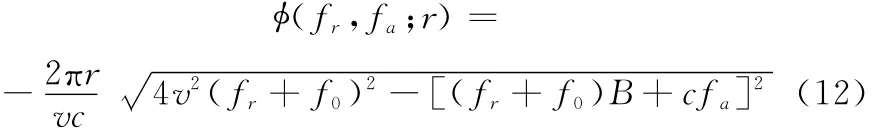
在窄带条件下，有fr≪f0，将式（12）对fr进行泰勒级数展开并保留二阶项，有

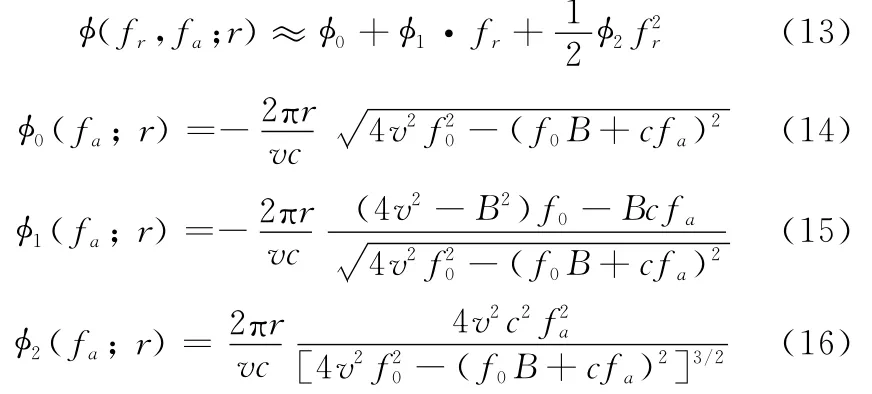
将式（13）～式（16）代入式（11），经过整理，点目标回波响应的二维谱为

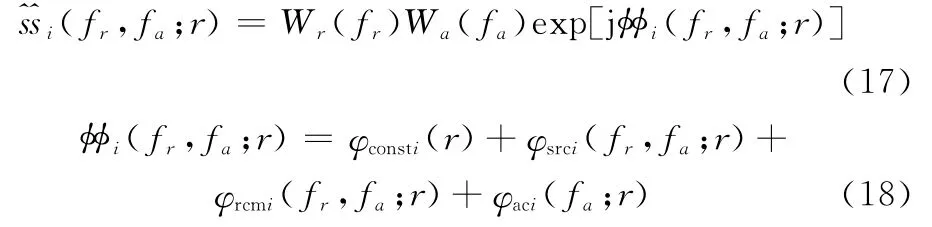
式中，第1个相位项φconsti（r）表示与距离频率和方位频率均无关的常数项，该项可以在任意域通过相位相乘予以消除，其表达式为

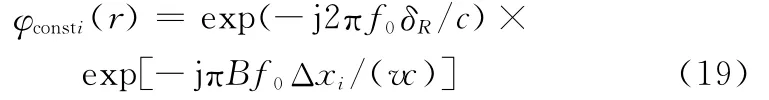
第2个相位项φsrci（fr，fa；r）表示方位频率和距离频率的二阶耦合项，是距离压缩（range compression，RC）和二次距离压缩（secondary range compression，SRC）的来源项，该项可以在二维频域通过相位相乘予以消除，其表达式为

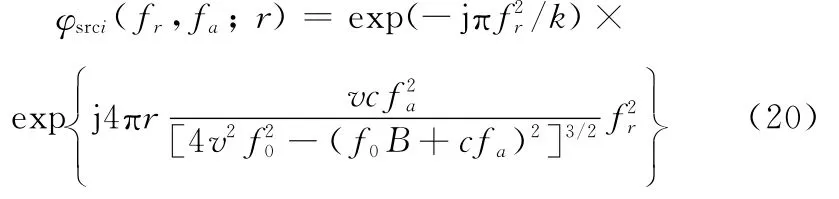
第3个相位项φrcmi（fr，fa；r）表示方位频率和距离频率的一阶耦合项，是距离徙动校正（range cell migration correction，RCMC）的来源项，该项可以在RD域通过sinc插值予以校正，其表达式为

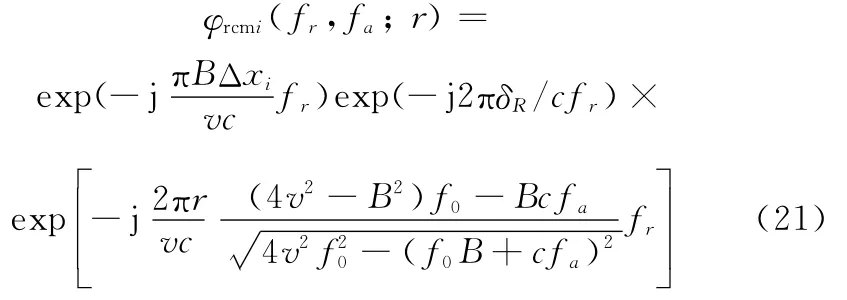
第4个相位项aci（fa；r）与距离频率无关，是方位走动校正（azimuth migration correction，AMC）和方位脉压（azimuth compression，AC）的来源项，该项可以在RD域通过相位相乘予以消除，其表达式为

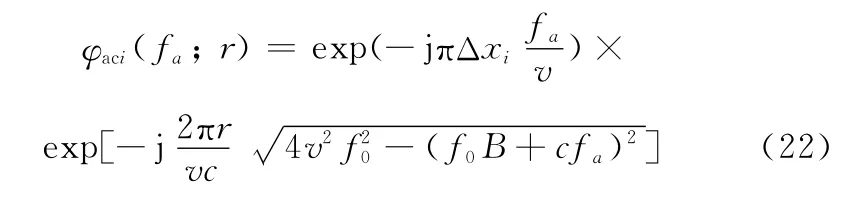
2.2 多子阵RD算法

经过推导，式（17）给出了多子阵SAS点目标响应的二维谱，这为后续设计快速的多子阵RD算法奠定了基础。依据上节对式（18）中各个相位项的分析，首先需要通过相位相乘补偿不同子阵的回波响应的固定相位项，该过程可以在距离频域方位时域进行。依据式（19）可以确定固定相位补偿因子为

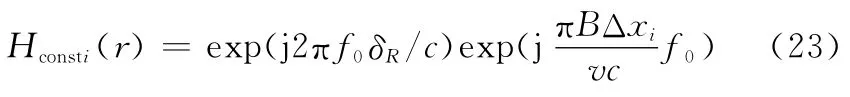
需要注意的是，式（17）仅为接收阵i接收到的回波响应的二维谱。对于多子阵SAS系统而言，单个接收阵的回波响应二维谱在方位向是欠采样的［15］，这是由多子阵SAS系统的工作方式决定的。如果直接对式（17）进行处理，会导致严重的图像散焦问题。

为了解决这个问题，通常对欠采样的方位谱进行扩展。具体做法分为两步：第一步将单个子阵欠采样的二维谱复制N次，N表示多子阵SAS系统使用的接收阵数量；第二步将N个相同的二维谱沿方位向进行首尾相接排列。显然，单个子阵欠采样的二维谱将被扩展为原来的N倍，这就是单个子阵二维谱的方位谱扩展过程，其主要目的是使得扩展后的二维谱满足采样要求，进而利用单阵收发合置RD算法对单个子阵的回波响应进行处理。

RC和SRC通常在二维频域通过相位相乘实现，依据式（20）可以确定RC和SRC参考因子为

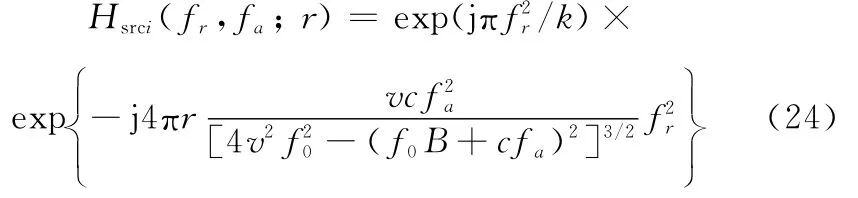
这样就完成了RC和SRC。然后，将回波响应沿距离向作逆FT回到RD域以完成RCMC和方位向处理，RCMC通常通过sinc插值实现。依据式（21）并结合距离多普勒域的回波响应可以确定距离徙动量为

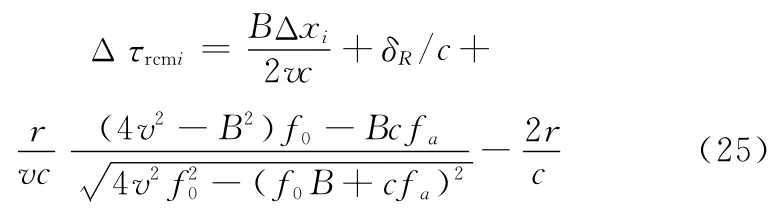
方位向处理主要包括AMC和AC，通常在RD域通过相位相乘实现。依据式（22）可以确定AMC和AC的参考因子为

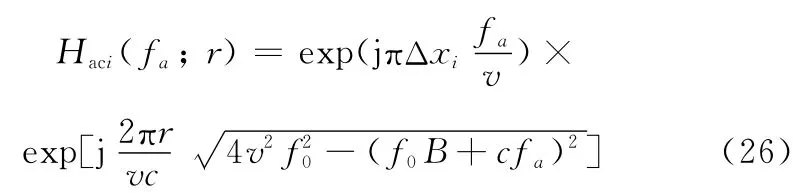
对于单阵SAS而言，可以沿方位向作逆FT回到二维时域以获得SAS图像，但是对于多子阵SAS而言，仅通过单一子阵回波响应重建的图像是相当模糊的。方位谱扩展虽然增加了二维谱的数量，使单个子阵的二维谱满足单独成像的要求，但是并没有增加任何有效的信息量。为了得到高分辨的SAS图像，需要充分利用不同接收阵回波信号之间的相干性，通过相干叠加实现高分辨SAS图像的重建。相干叠加之后，通过方位向逆FT回到二维时域即可获得高分辨的多子阵SAS图像。图3绘制了本文所提多子阵SAS RD算法的结构图。

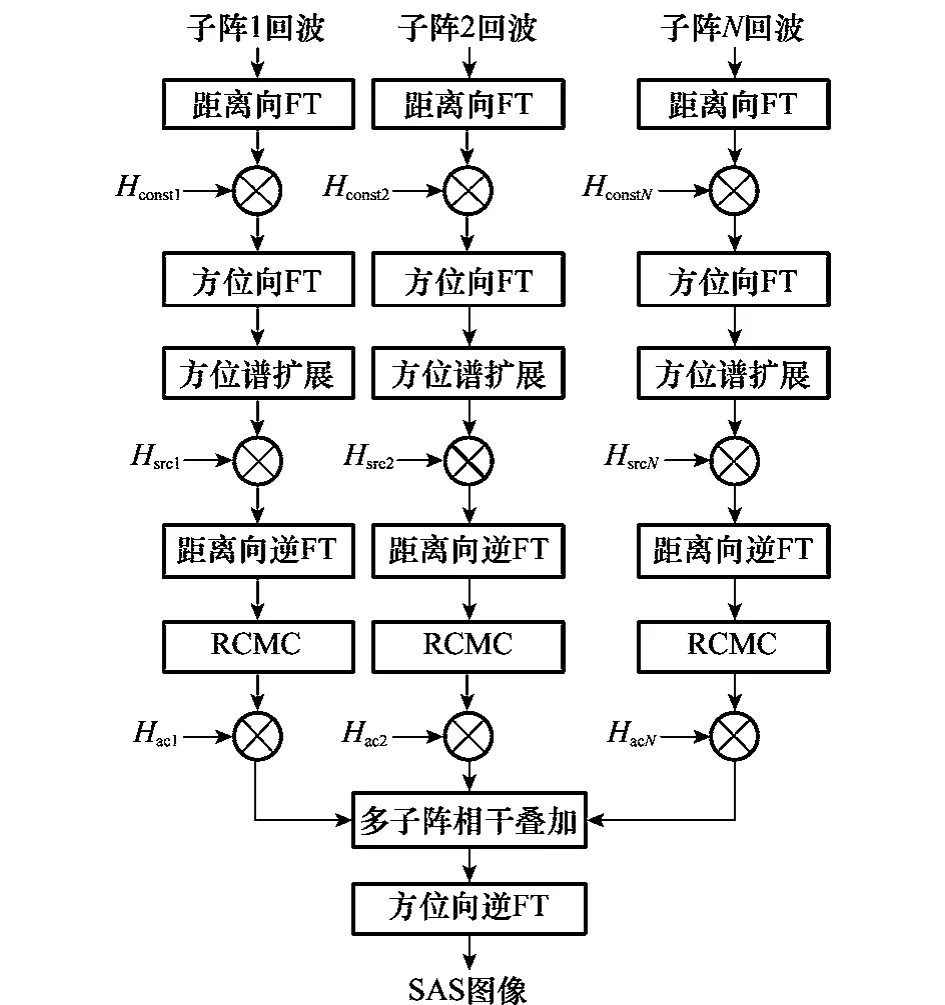
图3 多子阵SAS RD算法结构图

3 仿真试验和实测数据成像结果

3.1 仿真试验

为了验证上述分析及所提算法的有效性，进行了仿真试验，仿真参数如下：中心频率为150 k Hz，发射阵和接收阵长度均为8cm，信号带宽为40 k Hz，脉冲重复间隔为0.2 s，信号时宽为20 ms，SAS平台航速为2.5 m／s。成像场景为分别位于（0 m，55 m）、（1 m，54 m）、（1 m，56 m）、（－1 m，54 m）和（－1 m，56 m）的5个孤立的点目标。仿真过程利用基于修正的DPC近似的RD算法［11］和本文算法对成像场景的回波响应进行处理，处理过程中距离向和方位向均不进行任何加权。

图4绘制了仿真试验结果，其中图4（a）为基于修正DPC近似的RD算法［11］对成像场景内点目标回波响应的处理结果，图4（b）为本文算法的处理结果，横坐标表示距离向，纵坐标表示方位向，点目标响应强度用能量进行归一化，取值范围为－40～0 d B。从图4（a）可以看出，基于修正DPC近似的RD算法的处理结果在方位向存在着虚假目标，这可能是由于较高的副瓣所致。造成这种现象的主要原因是由于该距离上修正的DPC近似引入的相位误差已经超过临界值π／8，难以满足高分辨成像的要求。相比之下，利用本文算法的处理结果则明显优于利用基于修正的DPC近似的RD算法的处理结果，如图4（b）所示，这也充分说明了本文算法的可靠性和有效性。

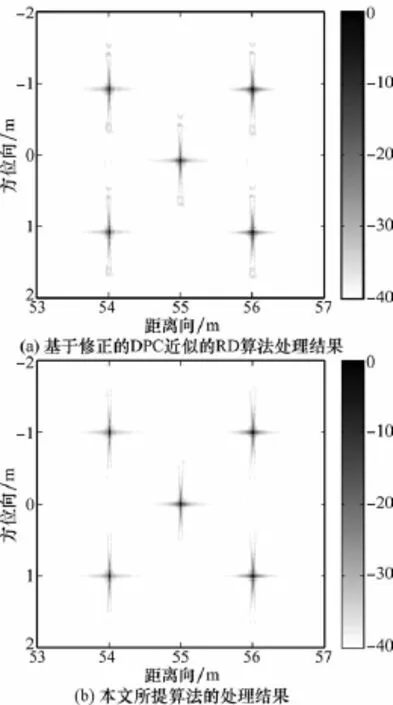
图4 仿真试验结果对比

3.2 实测数据成像结果

本节采用ChinSAS-150多子阵SAS系统在2010年千岛湖某航次录取的湖底地形数据进一步验证本文算法的有效性。该系统在高分辨模式下，工作参数与仿真试验使用的参数一致。成像场景为一个50 m×60 m的数据块，其中距离向为36～80 m，方位向为0～60 m。图5绘制了两种算法对成像场景内实测回波数据的重构结果，其中图5（a）为基于修正的DPC近似的RD算法重构的目标场景，图5（b）为本文算法重构的目标场景，横坐标表示距离向，纵坐标表示方位向，图像右侧的色彩条表示目标强度。

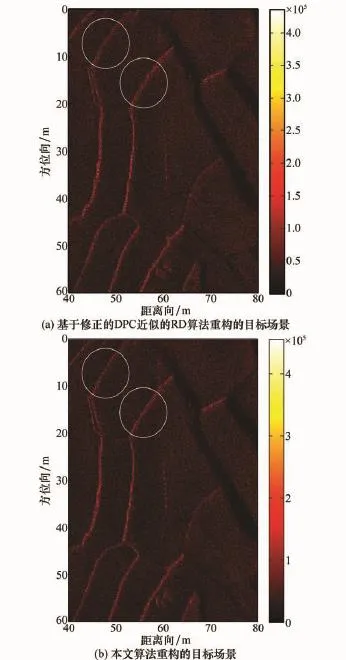
图5 实测数据成像结果对比

从整体上来看，两幅图像并无明显区别；但是从细节上来看，图5（b）具有比图5（a）更好的锐化效果，局部区域也更加清晰（图中的标注部分）。该结论与仿真试验结论相一致，进一步验证了本文算法的有效性。

4 结论

为了推导更加精确的点目标响应二维谱以设计快速的高分辨多子阵SAS成像算法，本文对修正的DPC近似进行改进，将双根号形式的距离历程表示为类收发合置项、距离空变项与方位空变一阶项之和的形式，不仅有效地解决了双根号形式距离历程带来的问题，而且大大提高了距离历程近似的精度。在利用驻定相位原理求取方位向驻定相位点的过程中，由于充分考虑了方位空变一阶项的影响，推导了更加精确的点目标响应二维谱。在此基础上，本文提出了一种适应于多子阵SAS高分辨成像的RD算法，仿真试验和实测数据成像结果验证了该算法的有效性。运动补偿对于提高成像精度有着极其重要的作用，如何将有效的运动补偿方法与本文算法相结合是下一步的主要工作。

［1］Callow H J，Hayes M P，Gough P T.Wavenumber domain reconstruction of SAR／SAS imagery using single transmitter and multiple-receiver geometry［J］.Electronics Letters，2002，38（7）：336- 338.

［2］Wang H T，Tang J S，Yuan B C.Research on a multi-receiver synthetic aperture sonar imaging algorithm based on FFT［J］.Journal of Harbin Engineering University，2009，30（7）：820- 823.（汪海涛，唐劲松，苑秉成.多子阵SAS逐线成像算法研究［J］.哈尔滨工程大学学报，2009，30（7）：820- 823.）

［3］Hansen R E，Callow H J，Sabo T O，et al.Challenges in seafloor imaging and mapping with synthetic aperture sonar［J］.IEEE Trans. on Geoscience and Remote Sensing，2011，49（10）：3677- 3687.

［4］Zhang X B，Tang J S，Zhang S，et al.Chirp-scaling algorithm for multi-receiver synthetic aperture sonar［J］.Systems Engineering and Electronics，2013，35（7）：1415- 1420.（张学波，唐劲松，张森，等.多接收阵合成孔径声呐线频调变标成像算法［J］.系统工程与电子技术，2013，35（7）：1415- 1420.）

［5］Cumming I G，Wong F H.Digital processing of synthetic aperture radar data：algorithms and implementation［M］.Norwood：Artech House，2005.

［6］Ding J S，Zhang Z H，Xing M D，et al.A new look at the bistaticto-monostatic conversion for tandem SAR image formation［J］.IEEE Geoscience and Remote Sensing Letters，2008，5（3）：392- 395.

［7］Zeng T，Wang R，Li F，et al.A modified nonlinear chirp scaling algorithm for spaceborne／stationary bistatic SAR based on series reversion［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（5）：3108- 3118.

［8］Tian Z，Tang J S，Zhong H P，et al.An effective multiple-receiver synthetic aperture sonar CSimaging algorithm［J］.Journal of Huazhong University of Science and Technology（Natural Science Edition），2014，42（8）：22- 26.（田振，唐劲松，钟何平，等.一种快速重建多子阵合成孔径声呐CS成像算法［J］.华中科技大学学报（自然科学版），2014，42（8）：22- 26.）

［9］Sheriff R W.Synthetic aperture beamforming with automatic phase compensation for high frequency sonars［C］∥Proc.of the IEEE Symposium on Autonomous Underwater Vehicle Technology，Annapolis，1992：236- 245.

［10］Jiang X K，Sun C，Feng J.A novel image reconstruction algorithm for synthetic aperture sonar with single transmitter and multiple-receiver configuration［C］∥Proc.of the IEEE Technology Ocean，2004：1940- 1944.

［11］Yang H L，Zhang S，Tang J S.Study on simulation of multiple-receiver synthetic aperture sonar imagery based on wide swath［J］.Journal of System Simulation，2011，23（7）：1424-1428.（杨海亮，张森，唐劲松.宽测绘带多阵合成孔径声呐成像的仿真研究［J］.系统仿真学报，2011，23（7）：1424- 1428.）

［12］Zhang X B，Tang J S，Zhong H P.Multireceiver correction for the chirp scaling algorithm in synthetic aperture sonar［J］.IEEE Journal of Oceanic Engineering，2014，39（3）：472- 481.

［13］Tang J S，Zhang C H，Li Q H.Multi-aperture synthetic aperture sonar imaging algorithm［C］∥Proc.of the Academic Forum of Chinese Youth，1999：235- 239.（唐劲松，张春华，李启虎.多子阵合成孔径声呐逐点成像算法［C］∥中国青年学术交流会，1999：235- 239.）

［14］Callow H J.Signal processing for synthetic aperture sonar image enhancement［D］.New Zealand：University of Canterbury，2003.

［15］Zhang Z H，Xing M D，Ding J S，et al.Focusing parallel bistatic SAR data using the analytic transfer function in the wavenumber domain［J］.IEEE Trans.on Geoscience and Remote Sensing，2007，45（11）：3633- 3645.

［16］Gough P T，Hawkins D W.Imaging algorithms for a strip-map synthetic aperture sonar：minimizing the effects of aperture error and aperture undersampling［J］.IEEE Journal of Oceanic Engineering，1997，22（1）：27- 39.

Effective range Doppler algorithm for focusing the multiple-receiver SAS data based on the modified DPC approximation

TIAN Zhen，TANG Jin-song，ZHANG Sen，ZHONG He-ping
（Naval Institute of Underwater Acoustic Technology，Naval University of Engineering，Wuhan 430033，China）

Because of ignoring the azimuth-variance of range history approximation error，the algorithm based on the conventional displacement phase center（DPC）approximation always suffers from some serious problems of azimuth migration and closer range defocusing.In order to solve these problems，a modified DPC approximation is proposed，which expresses the double-square-root form range history by the sum of a monostatic term，a range-variant term and an azimuth-variant term.By considering the azimuth-variant term in deriving the azimuth phase stationary point using the principle of stationary phase，a more accurate azimuth time phase stationary point is derived and the point target response two-dimensional spectrum is correspondingly improved.Based on that，a high resolution range Doppler algorithm is presented for the imaging of multiple-receiver synthetic aperture sonar（SAS）.The results of simulation and real data imaging show the effectiveness of the proposed algorithm.

multiple-receiver synthetic aperture sonar（SAS）；range Doppler（RD）algorithm；displacement phase center（DPC）approximation；azimuth-variance

TN 911.7

10.3969／j.issn.1001-506X.2015.12.12

田振（198-7- ），男，博士研究生，主要研究方向为多子阵合成孔径声呐成像算法、运动补偿方法。

E-mail：tianzhen15198＠163.com

唐劲松（1964- ），男，教授，博士后，主要研究方向为水声通信、合成孔径声呐成像、干涉合成孔径声呐成像。

E-mail：jinsongtangwh＠163.com

张森（1982- ），男，副研究员，博士，主要研究方向为水声通信、干涉合成孔径声呐成像。

E-mail：johnson_xh＠sina.com

钟何平（198-3- ），男，讲师，博士，主要研究方向为干涉合成孔径声呐成像、并行运算。

E-mail：zheping525＠sohu.com.cn

1001-506X（2015）12-2739-06