基于机载窄带雷达的舰船目标多普勒特性分析

2015-06-05杨秋，张群，王敏，孙莉

系统工程与电子技术 2015年12期

关键词：微动窄带时频

杨秋，张群，王敏，孙莉

（空军工程大学信息与导航学院，陕西西安710077）

基于机载窄带雷达的舰船目标多普勒特性分析

杨秋，张群，王敏，孙莉

（空军工程大学信息与导航学院，陕西西安710077）

针对机载窄带雷达探测海面非合作舰船目标识别能力不足问题，首先建立了舰船横滚、俯仰和偏航三维微动下舰船运动方程，在此基础上建立了窄带雷达探测舰船的回波信号模型，分析了回波信号多普勒频率成分及其特征。理论分析结果表明，舰船三维微动会导致雷达回波信号的多普勒频率相对无微动情况下出现频谱展宽；并且不同位置的散射点具有不同的时频变化曲线；在短时间内，各散射点微多普勒时频曲线以类似LFM形式的线性关系变化，在较长时间内以类似正弦信号形式周期性变化，其周期与横滚角变化周期相同。

窄带雷达；非合作舰船；微动；微多普勒

0 引言

无论在军用还是民用，海面舰船目标的分类辨识都具有重要应用价值［1］。光学和雷达传感器是目前探测海面舰船的主要手段，光学传感器分辨率高，且其图像易于识别，但存在的主要缺陷是受天气、烟雾等环境影响非常大，在实际使用中尤其是恶劣环境中非常受限；相比光学传感器，雷达传感器具有全天候、全天时、不受天气限制的显著优越性，因而在探测海面舰船等目标时受到了广泛应用。

利用雷达探测舰船通常都是基于宽带体制雷达的高分辨特性，利用高分辨图像进行识别的［26］。但由于宽带雷达信号处理复杂，数据量和运算量大、以及图像解译困难等制约性问题，目前大多数海基、岸基和机载雷达最基本和常态的应用模式_仍然是窄带模式［78］，如何利用窄带模式，在不影响雷达探测舰船目标距离、方位和速度等常规功能的前提下，获取目标更丰富的信息，进而提高对舰船的识别能力，具有一定的理论研究价值与较强的实际应用价值。

从公开发表的文献资料来看，针对该问题的研究成果十分少见，仅有文献［8］提出了一种对窄带雷达回波信号作傅里叶-梅林变换（Fourier-Mellin transform，FMT）后采用支持向量机区分不同类型舰船的新方法，该方法能够区别不同类型和吨位的舰船，但不能获取每艘舰船的新信息，即只能用于分类而不能用于识别。实际上，在利用窄带雷达探测海面运动舰船时，不仅存在舰船与载机雷达的相对宏观运动，由于螺旋桨、发动机和船舵等部件会产生一定的推动和控制，舰船姿态角会随着海浪而变化［9-10］，使得舰船还存在横滚、俯仰和偏航等微动。一方面，窄带雷达是利用回波信号的多普勒频率测速的，上述微动会对回波信号多普勒频率产生附加调制作用［1114］，导致回波信号的频谱出现展宽现象，对准确测量舰船速度等参数造成了一定的影响。但另一方面，舰船的微动参数与舰船类型和海情有关［15］，即可以作为一种新的特征参数用于目标分类和识别［16］，但微动舰船的窄带雷达回波信号特性分析及如何从回波信号中提取微动特征参数尚未有公开成果。

本文针对机载窄带雷达探测海面舰船的典型应用场景，重点分析含横滚、俯仰和偏航的舰船窄带雷达回波信号多普勒特性。在建立含横滚、俯仰和偏航三维微动的舰船运动模型基础上，通过分析窄带雷达回波信号的频域及时频域特征，进而估计出目标微动特征参数，提高窄带雷达系统的目标识别能力。

1 舰船运动数学模型

通常舰船被视为刚体目标，其运动由3个平动自由度和3个转动自由度共同组成［17］：其中平动是沿坐标轴的运动，是指刚体在运动过程中，其中任意两点的连线始终保持原来的方向，包括纵移、横摆和起伏运动；相对平动，转动比较复杂，本文只考虑定轴转动，是指刚体上各点都绕同一直线作圆周运动，而直线本身在空间的位置保持不变的转动，包括横滚、俯仰和偏航，如图1所示。本文在建立舰船运动数学模型时，只分析3个转动自由度的微动和舰船沿航向的宏观运动。

图1 舰船3个转动自由度微动示意图

根据机载雷达与舰船的运动方式，建立如图2所示的机载雷达探测舰船的几何模型。选取直角坐标系O-XYZ为参考坐标系，海平面为XOY平面。其中载机以速度vp水平匀速飞行，距离海平面高度为H，设O′点为舰船微动的旋转中心点，初始位置坐标为（xo，yo，0），以该点为坐标原点建立目标本地坐标系O′-X′Y′Z′，其中，O′Y′、O′X′和O′Z′分别为舰船横滚、俯仰和偏航微动的转动坐标轴，偏航角、横滚角和俯仰角分别记为θr、θa和θp，舰船沿航向运动速度为vs，其方向与载机运动方向在XOY平面的夹角为θ0。

已有研究表明［18］，舰船在海面上的横滚、俯仰和偏航微动虽然呈现多倍周期和随机性的特点，但可以用钟摆模型近似。设横滚、俯仰和偏航钟摆模型的振幅和角频率分别为Aa、Ap、Ar和ωa、ωp、ωr，则各自旋转角可表示为

图2 机载雷达探测舰船目标的几何模型

经过时间t，载机从P′点沿直线运动到P″点，舰船旋转中心点由O′匀速移动到O″，为了建模方便，舰船散射点用目标本地坐标系O′-X′Y′Z′中的坐标（xT0，yT0，zT0）表示，则由于横滚、俯仰和偏航微动，O″处目标运动坐标系不再平行于O′-X′Y′Z′，需要通过旋转矩阵Rrot计算O″处运动舰船散射点在目标本地坐标系中对应的坐标，最后统一转换为参考坐标系O-XYZ中的坐标。

其中

且

舰船散射点在O′－X′Y′Z′中坐标为

进一步地，可得舰船散射点在O-XYZ中的坐标为

式中，Rinit为由O′-X′Y′Z′向O′-XYZ变换的欧拉旋转矩阵，其表达式为

将式（3）、式（4）和式（6）代入式（5），可得

式中

由式（7）可知，目标散射点在参考坐标系中的实时位置由3部分组成：第1部分是舰船横滚、俯仰和偏航微动引起的；第2部分是舰船沿航向的平动引起的；第3部分是舰船初始位置。根据复合函数和三角函数周期性，不难证明：

（1）Rx（θa）、Ry（θp）和Rz（θr）具有周期性，其周期分别与θa、θp和θr周期相同；

（2）旋转矩阵Rrot具有周期性，其周期为θa、θp和θr各自周期的最小公倍数。

结合图2可得雷达与目标散射点距离为

根据坐标轴旋转基本原理，显然有

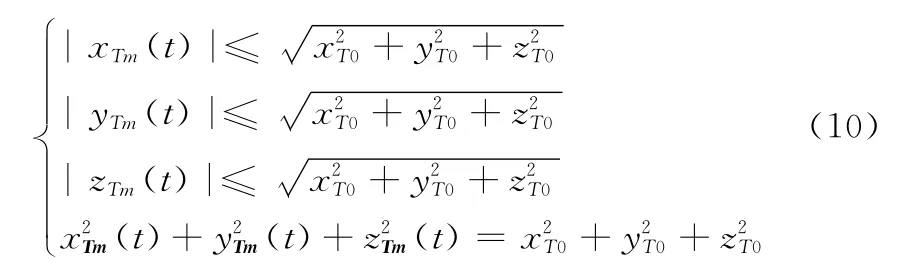
参考典型船体计参数［19］及各国航空母舰和驱逐舰等舰船［20］，如表1所示。现有舰船尺寸都满足｜xT0｜＜50，｜yT0｜＜200，｜zT0｜＜50，因此式（7）中｜xTm（t）｜，｜yTm（t）｜和｜zTm（t）｜的最大值也仅为 150■2 m。由于目标处于雷达远场，通常情况下机载雷达距离舰船至少为数十公里，目标尺寸远远小于雷达与目标之间的初始距离，即舰船目标最近和最远散射点与机载雷达之间的距离差相对于机载雷达与舰船之间的宏观距离是十分微弱的，而且目标在窄带雷达系统中是以单点目标存在的，因而在计算舰船与雷达之间距离，可以不用考虑微动对测距的影响，令vssinθ0＝vsx，vscosθ0＝vsy，有

则将式（11）求导可得

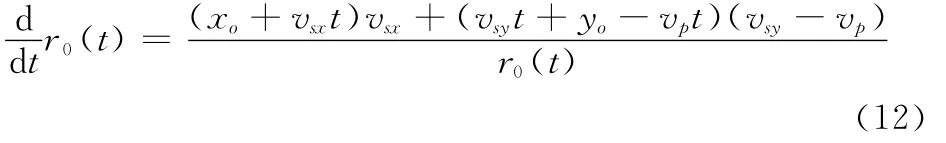
（2）当（vp－vsy）yo－vsxxo＞0时，则t≤t0时，舰船与雷达之间距离越来越近；t＞t0时，舰船与雷达之间距离越来越远，即舰船与雷达之间距离先变近后逐渐变远。

表1 _各国典型航空母舰和驱逐舰尺寸参数 m

2 雷达回波信号建模与多普勒特性分析

设雷达发射载频为fc的连续波信号，即

则各散射点回波信号为

式中，σ为散射点电磁散射系数。将s（t）变换为基带信号，得

间求导，得到回波多普勒频率为

对式（9）两边同时对t求导，有

进一步地，式（17）可以表示为

根据式（7），有

在上述运动舰船三维微动数学模型中，角频率与舰船类型有关［21］，而振幅与海情、舰船类型、舰船的航速和航向等因素有关。五级海情下航空母舰和驱逐舰的三维微动参数［15］如表2所示。

表2 五级海情下舰船三维微动参数

由表2可知，实际舰船的微动振幅是很小的，并且周期较长，即舰船以微弱幅度、缓慢地进行三维微动。根据三角函数泰勒展开式，有

式中，o（·）表示θ的高阶无穷小。

因而当θ很小时，总有sinθ＝θ，cosθ＝1成立。由表2可知，无论是驱逐舰还是航空母舰，θp和θr都很小，因此总有以下式子成立：

将式（20）代入式（18），并忽略其中的微弱量可得

式中

把式（21）中舰船和载机雷达宏观运动引起的变化项和舰船微动引起的多普勒频率分量分别记为fD和fm－D，可得

由于vp≫vs，舰船处于雷达远场，并且舰船尺寸及其三维微动相对都很小，因而在式（21）中，影响fd的主要频率成分仍然是fD，但fm－D会对fd产生附加频率调制。尽管不同位置散射点与雷达的视线方向不同，但由于目标处于雷达远场，因而其多普勒频率近似相等，如式（22）所示；由式（23）可知，由舰船三维微动引起的微多普勒频率是时变的，其大小与舰船目标散射点位置、三维微动参数及舰船初始位置及发射信号波长等参数有关，由于三维微动中俯仰角θp和偏航角θr相对于横滚角θa都很小，因而fm－D主要受θa调制，并且具有与θa相同的周期。进一步由表2可知，通常情况下横滚角变化周期都很大，即横滚角变化缓慢，因而在短时间内其微多普勒曲线可近似为类似于LFM形式的随时间线性变化曲线，在长时间内才能观测到其周期性。

3 仿真实验与结果分析

由于这里主要是验证窄带雷达探测舰船目标时存在的微多普勒效应及其特性，所以暂不考虑散射点遮挡效应，并且认为各散射点散射系数均为1，选取了表2中驱逐舰船头、船尾，左右两侧和桅杆顶5个散射点。主要仿真参数包括：雷达载频10 GHz，高度5 000 m，运动速度250 m／s；舰船中心初始位置（30 000 m，40 000 m，0），其航向与载机航向海平面夹角为30°，航速为30节。另外，由于实际环境中存在噪声和杂波，机载雷达在探测海面舰船目标时具有较高的信噪（杂）比［21］，因此回波信号中加入了信噪（杂）比为－5 dB的噪声。

为了对比分析舰船三维微动对窄带雷达回波信号频谱的影响，对无三维微动和有三维微动两种情况下雷达回波信号进行傅里叶变换，结果如图3所示。

对比图3（a）和图3（b），显然舰船的三维微动对回波信号频谱产生了附加的频谱调制，进而导致了回波信号频带相对无微动情况下出现了一定的展宽效应。将回波信号中由舰船和载机雷达宏观运动补偿后的信号频谱如图4所示。

图3 有无微动情况下回波信号频谱对比

图4 补偿舰船与雷达宏观运动后信号频谱

由图4可知，由舰船横滚、俯仰和偏航三维微动引起的目标回波信号中的微多普勒频带较窄，并且以0频率为中心。虽然图3和图4给出了回波信号傅里叶变换结果，但由于傅里叶变换无法反映信号频率随时间的变化关系，只能给出一个总的频率分布。为此采用时变信号分析常用的Gabor变换对上述回波信号进行分析，得到舰船无三维微动、有三维微动和宏观运动补偿后3种情况下信号的时频图，如图5所示。

图5 3种情况下回波信号Gabor变换时频图

由图5（a）可知，由舰船和载机宏观运动引起的不同散射点回波信号多普勒频率基本相同，因此仅靠多普勒频率很难得到目标速度外的其他信息；由图5（b）和图5（c）可以看出，尽管窄带雷达不具有宽带雷达具有的高分辨特征，但由于目标存在横滚、俯仰和偏航三维微动，导致了不同位置散射点的回波信号具有不同的时频曲线；尽管不同位置散射点回波信号的时频曲线不同，但都具有类似于正弦信号的变化规律。仿真结果验证了第3小节的理论分析结论。

最后仿真驱逐舰和航空母舰两种目标回波信号多普勒特性，其中驱逐舰参数不变；航空母舰也选择了表1中航空母舰船头、船尾，左右两侧和桅杆顶5个散射点，微动参数见表2，其他仿真参数与前面相同，仿真宏观运动补偿后不同类型舰船时频图如图6所示。

图6 不同类型舰船回波信号Gabor变换时频图

由图6可知，不同类型的舰船微多普勒特性是不相同的，在相同海情下，航空母舰微动振幅比驱逐舰小得多，因此其微多普勒曲线幅度也较小。进一步地，利用滑动自相关函数对图6驱逐舰和航空母舰两类目标的时频图进行周期检测，估计得到的两类目标回波信号时频图周期分别为驱逐舰＝12.19 s航空母舰＝26.22 s。参考表2，该周期非常接近驱逐舰和航空母舰的横滚角周期Ta驱逐舰＝12.2 s，Ta航空母舰＝26.4 s。实验表明该参数可以作为一种新的特征参数，用于舰船目标分类和识别，增强机载窄带雷达对舰船目标的分类与识别能力。

4 结论

针对机载窄带雷达探测海面非合作舰船目标时的识别能力不足问题，本文通过对回波信号进行时频分析和时频图参数估计，得到了可用于目标分类和识别的横滚角周期参数。通常情况下海情是可以通过其他途径得到的，根据海情信息和回波信号时频曲线估计各散射点位置信息，获取类似于高分辨雷达的结构可视化特征参数，进而反演目标的形状、材质等属性参数，是本文下一步的研究内容；同时，本文在考虑噪声和干扰时主要考虑了较高信噪（杂）比的情况，因此对低信噪（杂）比的情况下该问题的研究也是下一步的研究方向。

［1］Alexandrov C，Draganov A，Kolnv N.An application of automatic target recognition in marine navigation［C］∥Proc.of the IEEE Record of International Radar Conference，1995：250- 255.

［2］Wu L，Wei X Z，Yang D G，et al.ISAR imaging of targets with complex motion based on discrete chirp Fourier transform for cubic chirps［J］.IEEE Trans.on Geosciences and Remote Sensing，2012，50（10）：4201- 4212.

［3］Wang Y H，Liu H W.A hierarchical ship detection scheme for high-resolution SAR images［J］.IEEE Trans.on Geoscience and Remote Sensing，2012，50（10）：4173- 4184.

［4］Gao Y X，Yu Y，Zhang B，et al.Analysis on characteristics of ship target imaging by shipborne ISAR［J］.Journal of Telemetry，Tracking and Command，2013，34（1）：7- 12.（高悦欣，于勇，张彬，等.舰船ISAR对舰船目标成像特性分析［J］.遥测遥控，2013，34（1）：7- 12.）

［5］Zhang L X，Yang J.ship detection method based on polarimetric SAR［J］.Systems Engineering and Electronics，2010，32（10）：2081- 2085.（张瓅鑫，杨健.基于极化合成孔径雷达的舰船检测方法［J］.系统工程与电子技术，2010，32（10）：2081- 2085.）

［6］Luo X B，Fan H Q，Song Z Y，et al.Range profiles extraction for maritime formation targets based on range-azimuth clustering［J］.Systems Engineering and Electronics，2013，35（7）：1353- 1361.（罗小波，范红旗，宋志勇，等.基于距离方位二维聚类的海上编队目标距离像提取［J］.系统工程与电子技术，2013，35（7）：1353- 1361.）

［7］Wang F Y，Luo D，Liu H W.low-resolution airborne radar aircraft target classification［J］.Journal of Radars，2014，3（4）：444- 449.（王福友，罗钉，刘宏伟.低分辨机载雷达飞机目标分类识别技术研究［J］.雷达学报，2014，3（4）：444- 449.）

［8］Li Q，Li B，Hu W J，et al.ship target classification based on the low bandwidth marine radar［J］.Modern Radar，2012，34（12）：45- 49.（李青，李斌，胡文俊，等.基于低分辨率雷达的海面舰船目标分类识别技术［J］.现代雷达，2012，34（12）：45- 49.）

［9］Chen X L，Guan J，Bao Z H，et al.Detection and extraction of target with micro motion in spiky sea clutter via short-time fractional Fourier transform［J］.IEEE Trans.on Geoscience and Remote Sensing，2014，52（3）：1002- 1018.

［10］Tian J，Cui W，Wu S.A novel method for parameter estimation of space moving targets，［J］.IEEE Trans.on Geoscience and Remote Sensing，2014，11（2）：389- 393.

［11］Chen V C，Li F.Analysis of micro-Doppler signatures［J］.IEEE Proceedings Radar，Sonar&Navigation，2003，150（4）：271- 276.

［12］Chen V C，Li F，Ho S S.Micro-Doppler effect in radar：Phenomenon，model and simulation study［J］.IEEE Trans.on Aerospace and Electronic Systems，2006，42（1）：2- 21.

［13］Chen X Y，Liu Y X，Jiang W D，et al.Micro-motion resolution of radar targets［J］.Systems Engineering and Electronics，2007，29（3）：361- 364.（陈行勇，刘永祥，姜卫东，等.雷达目标微动分辨［J］.系统工程与电子技术，2007，29（3）：361- 364.）

［14］Gao H W，Xie L G，Wen S L.Modeling simulation and experiment of micro-Doppler signature of precession［J］.Journal of System Engineering and Electronics，2010，21（4）：544- 549.

［15］Du L L，Ren Y，Chen Z P.Analysis of Doppler characteristics in ship target ISAR imaging［J］.Signal Processing，2009，25（8A）：549- 553.（杜琳琳，任艳，陈曾平.舰船目标ISAR成像多普勒特性分析［J］.信号处理，2009，25（8A）：549- 553.）

［16］Chen X L，Guan J，He Y.Application and prospect of micromotion theory in the detection of sea surface target［J］.Journal of Radars，2013，2（1）：123- 134.（陈小龙，关键，何友.微多普勒理论在海面目标检测中的应用及展望［J］.雷达学报，2013，2（1）：123- 134.）

［17］Xu X J，Jiang D，Li X F.Modeling of dynamic radar signatures for ships on time-varying sea surface［J］.Systems Engineering and Electronics，2011，33（1）：42- 47.（许小剑，姜丹，李晓飞，等.时变海面舰船目标动态雷达特征信号模型［J］.系统工程与电子技术，2011，33（1）：42- 47.）

［18］Lei J，Xing M D，Bao Z.A method of ISAR ship imaging based on pendulum module［J］，Journal of Electronics&Information Technology，2006，28（1）：1- 6.（雷杰，邢孟道，保铮.一种基于钟摆模型的舰船目标成像方法［J］.电子与信息学报，2006，28（1）：1- 6.）

［19］Love L J，Jansen J F，Pin F G.On the modeling of robots operating on ships［C］∥Proc.of the IEEE International Conference on Robotics and Automation，2004：2436- 2443.

［20］Jiang L G.Concise world’s ships almanac［M］.Beijing：China Ocean Press，2002：39- 44，133- 150.（姜来根.简明世界舰船年鉴［M］.北京：海洋出版社，2002：39- 44，133- 150.）

［21］Wehne D R.High resolution radar［M］.Boston：Artech House，1987：273- 334.

［22］Zhang Y，Jiang Y C，Li H B.Improving synthetic aperture radar imaging of ship targets［J］.Chinese Journal of Radio Science，2009，24（4）：588- 592.（张云，姜义成，李宏博.一种改善SAR对舰船目标成像质量的新方法研究［J］.电波科学学报，2009，24（4）：588- 592.）

Doppler feature analysis of ship based on airborne narrow band radar

YANG Qiu，ZHANG Qun，WANG Min，SUN Li
（Institute of Information and Navigation，Air Force Engineering University，Xi’an 710077，China）

For the problem of the identify capability of non-cooperative ship on the sea in the narrow band airborne radar system，the three-dimensional micro-motion equations included yaw，pitch and row of uniform linear moving ship are built firstly.Then the periodicity characteristic and effects to the distance between radar and ship’s scatter point are analyzed.The echo of single frequency continuous wave radar is obtained then，composition and characteristics of echo Doppler frequency are researched finally.Theoretical analyses results show that the three-dimensional micro-motion may lead to spectral expansion and different time-frequency curves of each scattering point.Furthermore，the time-frequency curves change linearly like the linear frequency modulated（LFM）signal in short time，but in long time，they change irregularly in the complex sinusoidal form.

narrow band radar；non-cooperative ship；micro-motion；micro-Doppler

TN 95

10.3969／j.issn.1001-506X.2015.12.11

杨秋（198-6- ），通信作者，男，博士研究生，主要研究方向为雷达信号处理。

E-mail：yangqiu1105＠163.com

张群（196-4- ），男，教授，博士，主要研究方向为雷达信号处理与目标识别。

E-mail：zhangqunnus＠gmail.com

王敏（1975- ），女，副教授，博士，主要研究方向为图像信号处理。E-mail：wang_min5460＠sina.com

孙莉（197-9- ），女，讲师，博士，主要研究方向为雷达信号与图像处理。

E-mail：sl_lxa＠mail.nwpu.edu.cn

1001-506X（2015）12-2733-06

2014- 10- 08；