不确定系统鲁棒稳态白噪声反卷积平滑器

2015-06-05刘文强王雪梅邓自立

系统工程与电子技术 2015年12期

关键词：鲁棒协方差稳态

刘文强，王雪梅，邓自立

（1.黑龙江大学电子工程学院，黑龙江哈尔滨150080；

2.黑龙江科技大学计算机与信息工程学院，黑龙江哈尔滨150022）

不确定系统鲁棒稳态白噪声反卷积平滑器

刘文强1，2，王雪梅1，邓自立1

（1.黑龙江大学电子工程学院，黑龙江哈尔滨150080；

2.黑龙江科技大学计算机与信息工程学院，黑龙江哈尔滨150022）

对于带不确定噪声方差的线性离散时不变随机系统，根据极大极小鲁棒估计原理，基于带噪声方差保守上界的最坏情形保守系统，应用Kalman滤波和最优白噪声估计理论，提出了一种鲁棒稳态白噪声反卷积平滑器。对于所有容许的不确定噪声方差，保证它的实际平滑误差方差阵有一个最小上界。基于Lyapunov方程方法证明了它的鲁棒性和鲁棒精度关系。一个数值仿真例子验证了所提出结果的正确性和有效性。

不确定噪声方差；白噪声反卷积；鲁棒性；Lyapunov方程方法

0 引言

反卷积是信号处理中的一类基本问题，是指通过测量输出重构未知输入的过程。随机系统的输入白噪声估计问题称为白噪声反卷积。这类问题出现在许多领域中，例如通信和信号处理［13］，且在近年来受到广泛关注。目前，已经提出的反卷积方法包括Kalman滤波方法［13］、现代时间序列分析方法［4］和多项式方法［5］。

在文献［1- 3］中，基于Kalman滤波方法，提出了以石油地震勘探为应用背景的固定滞后最优白噪声反卷积平滑器。在文献［4］中，基于现代时间序列分析方法，提出了统一的白噪声估计理论，不仅包含输入白噪声估值器，而且还包含了观测白噪声估值器。基于Kalman滤波方法的最优白噪声估计理论已经推广到信息融合白噪声最优反卷积估值器［67］中。_________

基于Kalman滤波方法的最优白噪声估计理论有一个关键的假设，即系统的模型参数和噪声方差是精确已知的。然而，在实际应用中，由于建模误差或未建模动态等原因，这个假设并不总是满足。这推动了针对不确定系统的鲁棒Kalman滤波的许多研究。对于带不确定模型参数的系统，设计鲁棒Kalman滤波器主要有两种方法，即Riccati方程方法［89］和线性矩阵不等式方法［10］。这两种方法的缺点是仅仅假定了系统的模型参数是不确定的，而噪声方差则假定是已知的。鲁棒滤波器的性能指标是保证对所有容许的不确定性，相应的实际滤波误差方差有一个最小上界。

最近，对于带不确定噪声方差的多传感器系统，基于极大极小鲁棒估计准则［11］，在文献［12- 14］中分别提出了鲁棒局部和加权融合时变与稳态Kalman滤波器、预报器和平滑器，并提出了证明鲁棒性的Lyapunov方程方法。然而，到目前为止，针对不确定系统的鲁棒反卷积问题报道很少［11］，特别是鲁棒白噪声反卷积估计问题尚未见报道。

本文对带不确定噪声方差的系统，应用极大极小鲁棒估计准则，提出了一种固定滞后鲁棒稳态白噪声反卷积平滑器。

1 鲁棒稳态白噪声反卷积平滑器

考虑带不确定噪声方差的线性离散时不变系统

式中，t是离散时间；x（t）∈Rn是状态；y（t）∈Rm是观测；w（t）∈Rr是输入噪声；v（t）∈Rm是观测噪声；Φ，Γ和H是带适当维数的已知常阵。

假设1w（t）和v（t）是带零均值，且未知不确定实际（真实）方差分别为¯Q和¯R的不相关白噪声。Q＞0和R＞0分别是¯Q和¯R的已知保守上界，且满足

假设2线性离散时不变系统（见式（1）和式（2））是完全可控和完全可观的［15］。

问题是针对不确定系统式（1）和式（2），基于实际观测（y（t＋N），y（t＋N－1），…），设计输入白噪声w（t）的鲁棒反卷积平滑器^w（t｜t＋N）（N＞0为固定滞后且N为整数），使得对于所有容许的不确定噪声方差，保证它的实际平滑误差方差阵¯Pw（N）有一个最小上界Pw（N），即¯Pw（N）≤Pw（N）。这种性质也叫鲁棒性。

注1文献［3］指出，石油数据处理中的白噪声反卷积估计问题通常是离线进行的，不仅应用过去和现在的观测数据，还包括将来的观测数据。因此，本文给出的结果是用于事后平滑处理系统。由于当N≤0时，在假设1和假设2条件下，稳态最优白噪声滤波器（N＝0）和预报器（N＜0）为零［13］，故本文仅考虑固定滞后的白噪声平滑问题。

1.1 鲁棒稳态Kalman预报器

考虑带噪声方差保守上界Q和R的最坏情形保守系统式（1）和式（2），保守最优稳态Kalman预报器［16］为

式中，上标T为转置号；状态转移阵Ψp是稳定的；Kp为预报器增益；ε（t）为保守新息过程；Qε为保守新息过程方差；保守预报误差方差阵Σ满足Riccati方程

并且也满足如下Lyapunov方程

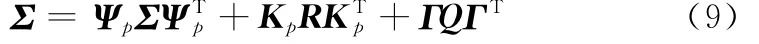
注2［13］在保守Kalman预报器式（4）中，保守观测y（t）是不可利用的，它由带噪声方差的保守上界Q和R的最坏保守系统式（1）和式（2）生成。只有实际观测y（t）是可利用（已知）的，它由带真实噪声方差¯Q和¯R的真实系统式（1）和式（2）生成。在式（4）中，用实际观测y（t）来代替保守观测y（t）可得到实际Kalman预报器。

实际预报误差x～（t＋1｜t）＝x（t＋1）－^x（t＋1｜t），这里x（t＋1）是实际状态，^x（t＋1｜t）是带实际观测y（t）的实际Kalman预报器。式（1）减式（4）得

应用式（10）得实际预报误差方差阵满足Lyapunov方程

引理1［13］对于带假设1和假设2的不确定系统式（1）和式（2），实际Kalman预报器式（4）是鲁棒的，即对于所有容许的满足式（3）的不确定噪声方差¯Q和¯R，有

且Σ是¯Σ的最小上界。实际Kalman预报器式（4）被称之为鲁棒Kalman预报器。

1.2 鲁棒稳态白噪声反卷积平滑器

对于带噪声方差保守上界Q和R的最坏情形保守系统式（1）和式（2），保守最优稳态白噪声反卷积平滑器［7］为

由射影理论［16］可得

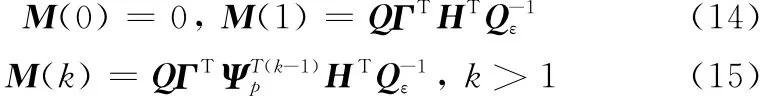
式中，ε（t）是由式（6）给出的保守新息过程；Qε是由式（7）给出的保守新息过程方差。

保守白噪声平滑误差方差阵为

根据文献［7］，保守白噪声平滑误差方差阵Pw（N）同样满足

其中，定义

注3在保守白噪声平滑器式（13）中，保守新息过程ε（t）是不可利用的，它由保守观测y（t）和保守预报器^x（t｜t－1）生成。仅仅实际新息过程ε（t）是可利用（已知）的，它由实际观测y（t）和实际Kalman预报器^x（t｜t－1）生成。在保守白噪声平滑器式（13）中，用实际新息过程ε（t）来代替保守新息过程ε（t），可得实际白噪声反卷积平滑器。

实际白噪声平滑误差为

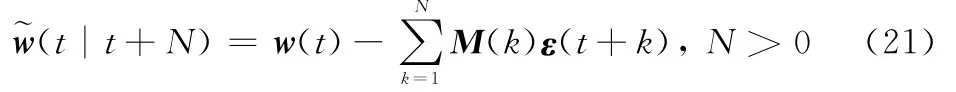
根据文献［7］，实际白噪声平滑误差~w（t｜t＋N）满足

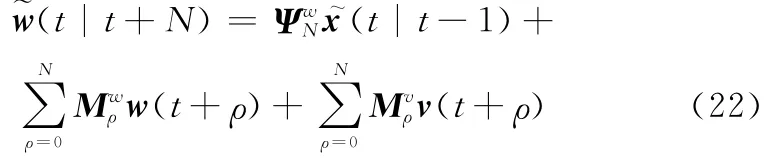
由于x～（t｜t－1）与w（t＋ρ）和v（t＋ρ）都是不相关的，故由式（22）得实际白噪声平滑误差方差阵满足

定理1对于不确定系统式（1）和式（2），在假设1和假设2条件下，实际白噪声平滑器式（13）是鲁棒的，即对于所有容许的满足式（3）的不确定实际噪声方差¯Q和¯R，有

且Pw（N）是¯Pw（N）的最小上界。此外，对于任意的两个正整数0＜N1＜N2，有

证明用式（17）减式（23）得

式中，定义ΔQ＝Q－¯Q；ΔR＝R－¯R。由式（12）可得Σ－¯Σ≥0，应用式（3）得ΔQ≥0，ΔR≥0。因此，由式（26）得Pw（N）－¯Pw（N）≥0，即式（24）成立。取¯Q＝Q，¯R＝R则约束条件（3）满足，比较式（9）和式（11），可得Σ＝¯Σ。因此由式（26），可得Pw（N）＝¯Pw（N）。对任意的其他上界P*w（N），有Pw（N）＝¯Pw（N）≤P*w（N），因此Pw（N）是¯Pw（N）的最小上界。由式（16）有

由式（27）和Qε＞0引出式（25）成立。证毕

称式（13）给出的实际白噪声反卷积平滑器为鲁棒白噪声反卷积平滑器。关系式（24）称为鲁棒白噪声反卷积平滑器的鲁棒性。

注4对式（24）取矩阵迹运算有

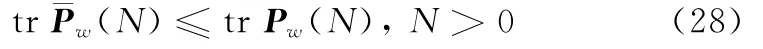
式中，tr表示矩阵的迹。由式（25）有

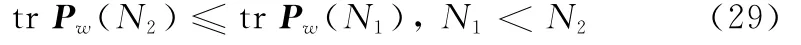
式中，tr Pw（N）为鲁棒白噪声反卷积平滑器的鲁棒精度或全局精度；tr¯Pw（N）为鲁棒白噪声反卷积平滑器的实际精度［12］。这意味着具有较小的tr Pw（N）或tr¯Pw（N）的平滑器具有较高的鲁棒或实际精度。

注5式（28）表明鲁棒白噪声反卷积平滑器的实际精度高于它的鲁棒精度，鲁棒精度是最低的（最坏的）实际精度。式（29）表明带较大固定滞后平滑器的鲁棒精度高于拥有较小固定滞后平滑器的鲁棒精度。即随着滞后步数N的增大，将提高鲁棒白噪声反卷积平滑器的鲁棒精度。

注6对于带不确定噪声方差的系统，就作者所知，本文给出的鲁棒白噪声反卷积平滑器为首次提出。这将文献［1］中给出的最优白噪声反卷积平滑器拓展到了带不确定噪声方差的系统。

2 仿真例子

随着滞后步数N的变化，表1给出了鲁棒白噪声反卷积平滑器的鲁棒和实际精度比较。

表1 鲁棒白噪声反卷积平滑器的鲁棒和实际精度比较

从表1可看出，无论滞后步数N在闭区间［1，9］内取何整数值，相应的鲁棒白噪声反卷积平滑器的实际精度都高于它的鲁棒精度，这验证了精度关系式（28）。此外，从表1还可看出，随着滞后步数N的增大，鲁棒白噪声反卷积平滑器的鲁棒精度在提高，这验证了精度关系式（29），但是当N增大到一定值时，其鲁棒精度趋于稳定值，这一点已在文献［17］中证明。

反应鲁棒白噪声反卷积平滑器的实际精度和鲁棒精度随着N变化的一个仿真图形如图1所示，同样验证了精度关系式（28）和式（29）。此外，可明显看出，鲁棒白噪声反卷积平滑器的鲁棒精度与N之间是一个非线性关系。

为了给出矩阵精度关系式（24）和式（25）的几何解释，方差阵P的协方差椭圆定义为点的轨迹｛x∶xTP－1x＝c｝，这里，P是n×n的方差矩阵，x∈Rn且c是一个常数。不失一般性，通常选择c＝1。在文献［18］中已经证明，方差阵P1≤P2等价于P1的协方差椭圆被包含在P2的协方差椭圆中。以N＝1，2，3为例，图2给出了鲁棒稳态白噪声反卷积平滑误差方差阵的协方差椭圆。从图2可看出，P－w（N）的协方差椭圆均被包含在它们的最小上界Pw（N）的协方差椭圆内，这验证了鲁棒性（24）。此外，从图2还可看出，Pw（3）的协方差椭圆被包含在Pw（2）的协方差椭圆内，而Pw（2）的协方差椭圆被包含在Pw（1）的协方差椭圆内，这验证了精度关系式（25）。

图1 实际精度和鲁棒精度随着N的变化情况

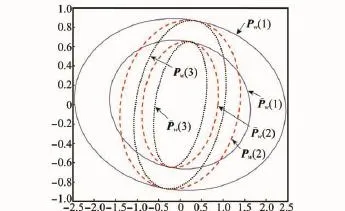
图2 鲁棒白噪声平滑误差方差阵的协方差椭圆比较

鲁棒白噪声反卷积平滑器的第一个分量的值与实际白噪声第一个分量的值之间的比较如图3所示。在图3中，直线端点的纵坐标值代表真实值，圆点的纵坐标值代表平滑估计。从图3中同样可看出，带较大固定滞后的平滑器的精度高于带较小固定滞后的平滑器的精度。

为了验证上述理论精度关系，进行ρ＝500次蒙特卡罗仿真实验。在时刻t时的均方误差值（mean square error，MSE）定义为

式中，N＝1，2，3，w（j）（t）或^w（j）（t｜t＋N）表示w（t）或^w（t｜t＋N）的第j个实现。鲁棒稳态白噪声反卷积平滑器的MSE曲线如图4所示，其中，直线代表相应的实际平滑误差方差阵¯Pw（N）的迹，曲线代表MSE（N）（t）的值。根据采样方差的一致性，有按概率收敛性

图3 w1（t）和^w1（t｜t＋N）（N＝1，3）的关系曲线

图4 鲁棒稳态白噪声反卷积平滑器的MSE曲线

从图4可以看出，当ρ和t充分大时，MSE（N）（t）的值接近于相应的实际平滑误差方差阵的迹值，这验证了一致性关系式（31）。

图5给出了N＝1，2，3时的累积平滑误差平方曲线比较。从图5可看出，带较大固定滞后平滑器的精度高于带较小固定滞后平滑器的精度，这与图3给出的结果是一致的。

注7Bernoulli-Gaussian白噪声可直观上看成取非零值稀疏化的Gaussian白噪声，它在石油地震勘探领域有重要的应用背景［1］。可用它来模拟油层反射系数序列，而估计反射系数序列，对寻找、发现油田和确定油田的几何形状有重要作用。在仿真实验中针对Bernoulli-Gaussian白噪声设计了鲁棒反卷积平滑器，仿真结果显示了其良好的性能。因而，本文提出的鲁棒白噪声反卷积平滑器可应用于石油地震勘探数据处理，具有重要实际意义。

图5 累积平滑误差平方曲线比较

3 结论

对于噪声方差不确定的线性离散时不变系统，根据极大极小鲁棒估计原理，基于带噪声方差保守上界的最坏情形系统，提出了鲁棒白噪声反卷积平滑器。应用Lyapunov方程方法证明了它的鲁棒性，并给出了鲁棒精度关系。推广到处理鲁棒信息融合白噪声反卷积问题正在研究中。

［1］Mendel J M.White noise estimators for seismic data processing in oil exploration［J］.IEEE Trans.on Automatic Control，1977，22（5）：694- 706.

［2］Mendel J M，Kormylo J.New fast optimal white-noise estimators for deconvolution［J］.IEEE Trans.on Geoscience Electronics，1977，15（1）：32- 41.

［3］Mendel J M.Optimal seismic deconvolution-an estimation-based approach［M］.New York：Academic Press，1983.

［4］Deng Z L，Zhang H S，Liu S J，et al.Optimal and self-tuning white noise estimators with approach to deconvolution and filtering problem［J］.Automatica，1996，32（2）：199- 216.

［5］Ahlen A，Sterned M.Optimal deconvolution based on polynomial method［J］.IEEE Trans.on Aconstics Speech and Signal Processing，1989，37（2）：217- 226.

［6］Sun S L.Multi-sensor information fusion white noise filter weighted by scalars based on Kalman predictor［J］.Automatica，2004，40（8）：1447- 1453.

［7］Sun X J，Gao Y，Deng Z L，et al.Multi-model information fusion Kalman filtering and white noise deconvolution［J］.Information Fusion，2010，11（2）：163- 173.

［8］Fu M，Souza C E，Luo Z Q.Finite-horizon robust Kalman filter design［J］.IEEE Trans.on Signal Processing，2001，49（9）：2103- 2112

［9］Zhu X，Soh Y C，Xie L H.Design and analysis of discrete-time robust Kalman filters［J］.Automatica，2002，38（6）：1069- 1077.

［10］Ebihara Y，Hagivara T.A dilated LMI approach to robust performance analysis of linear time-invariant uncertain systems［J］.Automatica，2005，41（11）：1933- 1941.

［11］Chen Y L，Chen B S.Minimax robust deconvolution filters under stochastic parametric and noise uncertainties［J］.IEEE Trans.on Signal Processing，1994，42（1）：32- 45.

［12］Qi W J，Zhang P，Deng Z L.Robust weighted fusion Kalman filters for multisensor time-varying systems with uncertain noise variances［J］.Signal Processing，2014（99）：185- 200.

［13］Qi W J，Zhang P，Nie G H，et al.Robust weighted fusion Kalman predictors with uncertain noise variances［J］.Digital Signal Processing，2014，30（1）：37- 54.

［14］Qi W J，Zhang P，Nie G H，et al.Robust weighted fusion time-varying Kalman smoothers for multisensor system with uncertain noise variances［J］.Information Sciences，2014（282）：15- 37.

［15］Kamen E W，Su J K.Introduction to optimal estimation［M］.London Berlin Heidelberg：Springer Verlag，1999.

［16］Kailath T，Sayed A H，Hassibi B.Linear estimation［M］.New Jersey：Prentice Hall，2000.

［17］Deng Z L.Optimal estimation theory with applications-modeling，filtering，and information fusion estimation［M］.Harbin：Harbin Institute of Technology Press，2005.（邓自立.最优估计理论及其应用建模、滤波、信息融合估计［M］.哈尔滨：哈尔滨工业大学出版社，2005.）

［18］Deng Z L，Zhang P，Qi W J，et al.Sequential covariance intersection fusion Kalman filter［J］.Information Sciences，2012（189）：293- 309.

Robust steady-state white noise deconvolution smoother for uncertain systems

LIU Wen-qiang1，2，WANG Xue-mei1，DENG Zi-li1
（1.Electronic Engineering College，Heilongjiang University，Harbin 150080，China；2.Computer and Information Engineering College，Heilongjiang University of Science and Technology，Harbin 150022，China）

For the linear discrete time-invariant stochastic system with uncertain noise variances，according to the minimax robust estimation principle，based on the worst-case conservative system with the conservative upper bounds of noise variances，applying Kalman filter and the optimal white noise estimation theory，a robust steady-state white noise deconvolution smoother is presented.Its actual smoothing error variances are guaranteed to have a minimal upper bound for all admissible uncertain noise variances.Its robustness and the robust accuracy relation are proved based on the Lyapunov equation approach.A simulation example is given to verify the correctness and effectiveness of the proposed results.

uncertain noise variances；white noise deconvolution；robustness；Lyapunov equation approach

O 211.64

10.3969／j.issn.1001-506X.2015.12.05

刘文强（1980-），男，讲师，博士研究生，主要研究方向为鲁棒Kalman滤波、多传感器信息融合。

E-mail：dengzili890＠163.com

王雪梅（1978-），女，讲师，博士研究生，主要研究方向为鲁棒Kalman滤波、多传感器信息融合。

E-mail：dengzili889＠163.com

邓自立（1938-- ），通讯作者，男，教授，博士研究生导师，主要研究方向为信息融合、鲁棒Kalman滤波、最优和自校正滤波、现代时间序列分析。

E-mail：dzl＠hlju.edu.cn

1001-506X（2015）12-2696-05

2014- 12- 30；

2015- 06- 04；网络优先出版日期：2015- 08- 18。