3-RPS并联机构静刚度建模方法

落海伟，张 俊，王 辉，黄 田

(1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 安徽工业大学机械工程学院，马鞍山 243032)

3-RPS并联机构静刚度建模方法

落海伟1，张 俊2，王 辉1，黄 田1

(1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 安徽工业大学机械工程学院，马鞍山 243032)

以三自由度并联动力头A3(3-RPS)为研究对象，提出了一种基于子结构综合和静态凝聚技术的静刚度建模和自重变形求解方法．建模过程中，将机构划分为动平台和RPS伸缩支链子结构，并综合考虑了铰链和支链弹性对静刚度的贡献．其中，球铰和转动副处理为具有等效刚度的集中质量虚拟弹簧；伸缩支链借助有限元软件和静态凝聚技术，建立了支链子结构质量矩阵和刚度矩阵；动平台处理为刚性质量块．通过引入变形协调条件，建立系统的整体刚度矩阵．研究结果表明，整机主刚度随机构位姿的变化而变化；在动平台连体坐标系下，3个方向线刚度呈对称分布且w向刚度最大；运动部件自重会导致动平台末端产生较大弹性变形．该方法所得静刚度变化规律通过实测结果进行了验证．

静刚度；并联机构；子结构综合；静态凝聚

并联机床具有结构稳定、承载能力强和运动学逆解简单等特点，正逐渐成为高速机床领域备受关注的热点，如已成功应用于航空领域高速切削的Tricept[1]系列和Z3头[2]等即是该类型机床的典型范例．基于此，有学者基于拓扑结构3-RPS(R为转动副，P,为移动副，S为球铰)，发明了一种具有1平2转(1T2R)3个自由度的并联动力头——A3头[3-4]，配以x、y两个平动自由度，即可形成一种新型结构的五坐标高速加工中心．

并联机构的静刚度是影响机床定位精度的重要因素．在静刚度预估方法中，最常用的为有限元分析法．虽然有限元软件预估精度高，但如果要预估整个工作空间中静刚度随位型的变化规律，需要反复修改有限元模型并重新划分网格[5]，耗时多，工作量大，且需要占用大量计算机资源．为便于进一步进行参数优化，一些学者提出了静刚度解析或半解析方法．

Gosselin[6]基于雅可比矩阵，借助虚功原理建立了仅考虑支链驱动刚度的并联机构静刚度模型．Majou等[7]在此方法基础上引入了铰链刚度，建立了三平动并联机构Orthoglide刚度模型．Xu等[8]在进一步引入螺旋理论的基础上建立了3-P RC的静刚度模型．Wang等[9]利用同样方法建立了6-P SS的静刚度模型，并通过特征值对末端静刚度在整个工作空间下的分布特性进行了分析．Li等[3]利用虚功原理和全雅可比矩阵建立了3-RPS并联动力头的静刚度半解析模型，并基于等刚度原则对结构尺度参数进行了优化．上述方法的基本原理是建立机构关节空间到机构末端的刚度映射，进而得到机构末端刚度值，但该方法只能获得机构末端的六自由度刚度矩阵，无法建立可以反映系统各节点静刚度特性的总体刚度矩阵．

通过建立系统总体刚度矩阵可以实现末端载荷与整机各节点变形的映射关系．Deblaise等[10]利用子结构综合法建立了Delta的总体刚度矩阵，并对负载作用下整机变形规律进行了分析，但该模型将支链简化为简单的空间梁单元．Goncalves等[11]利用同样方法建立了6-RSS总体刚度矩阵．Wu等[12]在利用子结构综合并考虑铰链刚度的基础上，建立了带冗余驱动的混联机床总体刚度矩阵，并通过实验进行了验证，但在该模型中，支链同样被简化为空间梁单元．由此可见，已有文献在总体刚度矩阵建模过程中，均对复杂支链体进行了简化处理，将支链处理为简单截面(矩形、圆型、圆环和中空矩形等)的空间梁单元[5,12]，导致其建模精度不足．

本文以3自由度并联动力头A3为对象，首先借助有限元软件和静态凝聚技术，建立支链子结构的刚度矩阵；其次在引入铰链变形协调条件的基础上，利用子结构综合构造系统总体刚度矩阵；然后对整机静刚度在工作空间中随位姿的变化规律和受重力影响的变形规律进行了分析；最后通过实测结果对静刚度的变化规律进行了验证．本文研究的目的旨在为A3头的进一步设计、改进以及实际应用提供重要的理论基础．

1 3-RPS并联机构运动学模型

1.1 3-RPS结构简介

图1所示为A3头CAD模型结构．该机构由动平台、静平台和3条结构相同的RP S支链构成，其中，每条支链采用伺服电机通过丝杠螺母进行驱动，实现沿z向的平动和绕x、y轴转动3个自由度(1T2R)．

图2 A3头结构示意Fig.2 Schematic diagram of the A3 head

1.2 3-RPS运动学分析

图2为A3头的结构示意．其中，Ai、Bi、Ci(i=1,2,3)分别为第i条支链中球铰中心、转动副中心和支链电机．动平台△A1A2A3与静平台△B1B2B3为正三角形，点A与B分别为其几何中心．在B点建立静平台连体坐标系BxByBzB，各轴方向如图2所示；在A点建立动平台连体坐标系Auvw，初始状态下各轴方向与BxByBzB平行；At为刀尖点，相对于坐标系Auvw为wt；在Bi(i=1,2,3)点建立支链参考坐标系Bixiyizi，各轴方向如图2所示；s2i(i=1,2,3)为A3头第i支链中移动副的单位方向矢量；qi(i=1,2,3)为第i条支链球铰与转动副之间的长度．

动平台连体坐标系Auvw相对于固定参考坐标系BxByBzB的姿态矩阵利用z- x- z欧拉角表示为

式中：ψ、θ、φ分别为进动角、章动角和自旋角；Rot为旋转矩阵．

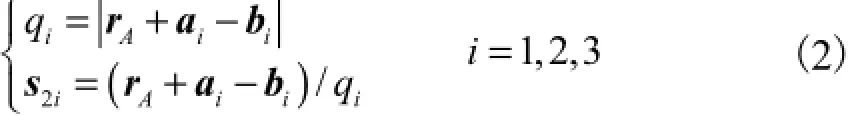
式中：rA为点A在坐标系BxByBzB的位置矢量；ai为球铰中心Ai相对于坐标系Auvw的位置矢量；bi为转动副中心Bi相对于坐标系BxByBzB的位置矢量，具体推导过程可参考文献[3]．

2 3-RPS子结构静力学模型

2.1 RPS支链子结构模型

因伸缩支链为复杂的几何体，支链内部为带筋的中空结构，为同时满足计算效率和求解精度，采用静态凝聚技术建立支链的刚度矩阵和质量矩阵．通过有限元软件ANSYS对支链进行前处理后，将质量矩阵和刚度矩阵导入MATLAB环境中进行自由度凝聚；节点iB(转动副中心)为虚拟凝聚点[13]，通过多点差值约束方程与支链在封闭框范围内的节点自由度uE连接，如图3所示．

图3 支链子结构自由度缩聚Fig.3 Limb substructural freedom reduction

根据有限元方法可写出支链的n自由度动力学方程为

式中：m、k分别为质量矩阵和刚度矩阵；u、f分别为支链的广义坐标列阵和外载荷列阵．将结构系统节点坐标划分为保留坐标au和凝聚掉的坐标bu，经排序和分块处理后得

式中：aam和aak分别为与保留坐标au对应的质量矩阵和刚度矩阵；bbm和bbk分别为与凝聚坐标bu对应的质量矩阵和刚度矩阵；abm、bam、abk和bak分别为分块后的交叉质量矩阵和刚度矩阵；af和bf分别为保留外载荷列阵和凝聚掉的外载荷列阵．根据静态凝聚技术基本思想，可得

根据结构系统凝聚前后动能与势能相等的原则，可得凝聚后的刚度矩阵、质量矩阵分别为

式中rm和rk分别为经静态凝聚后获得的质量矩阵和刚度矩阵．

因支链长度iq随机构位姿变化，在子结构综合时，随iq变化的对接节点无法满足相容条件[3,14]．为实现不相容条件下的子结构综合，在对接界面中心建立虚拟凝聚点iB，Eu为au中的界面对接自由度，则

式中：矩阵CT为界面节点自由度与凝聚节点自由度之间的传递矩阵，通过多点差值约束方程获取；B=u为界面自由度相对于支链广义坐标列阵的变换矩阵．

根据文献[13]可建立多点差值约束方程，则

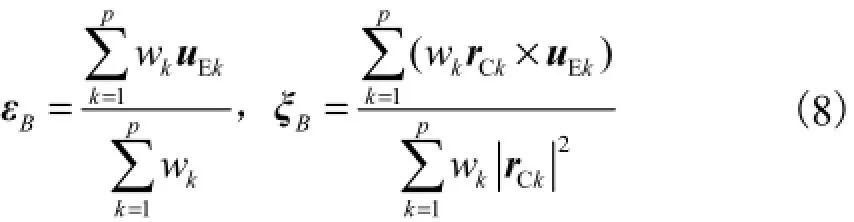
式中：Bε和Bξ分别为凝聚节点的3个平动自由度和3个转动自由度；Eku为Eu中第k个节点坐标；kw为权重系数，与对应界面节点所代表的接触区域成正比，具体选取过程可参考文献[14]；Ckr为虚拟节点到相应第k个界面节点的位置矢量；传递矩阵CT通过式(7)和式(8)确定．

根据支链的受力情况，整条支链可以看成是由两组弹簧支撑的空间梁结构[15]，其节点受力如图4所示，图中下标s和r分别代表球铰和转动副．

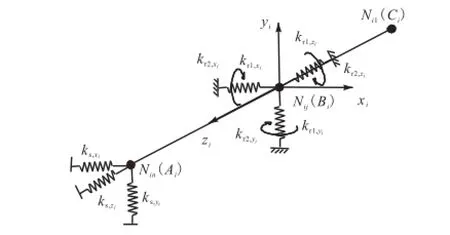
图4 支链受力示意Fig.4 Force diagram of limb

式中ik为经自由度缩聚后第i条支链的刚度矩阵．

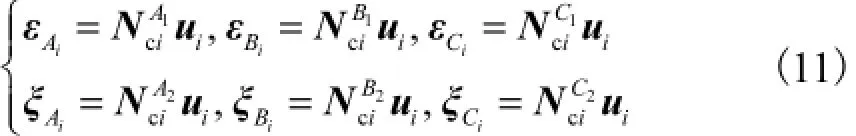
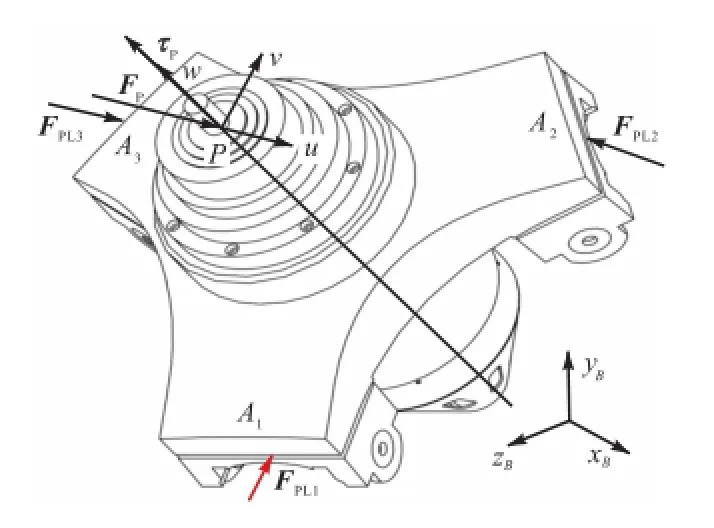
图5 动平台受力示意Fig.5 Force diagram of moving-platform

2.2 动平台子结构模型

动平台受力示意如图5所示．结合图5受力情况可写出动平台的动力学方程为

式中：FPLi为动平台与第i条支链间的作用力；rAi为动平台球铰链中心向量；FP、τP分别为动平台所受到的外部力和力矩；Ri为支链坐标系Bixiyizi到系统坐标系BxByBzB的变换矩阵．

3 3-RPS子结构综合

3.1 变形协调条件

动平台和支链间的位移关系如图6所示，图中，AiM、AiL分别表示连接界面上动平台和支链上的点；∇Ai、εAi分别为AiM、AiL在支链坐标系Bixiyizi下的位移．

图6 球铰链连接示意Fig.6 Connection of the sphere joint

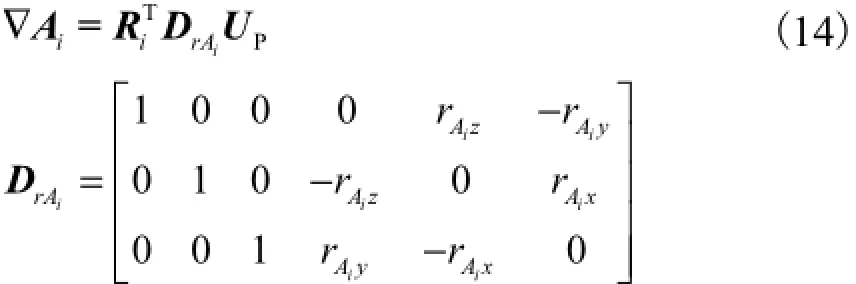
式中rAix、rAiy和rAiz分别为Ai点在坐标系BxByBzB下向量iAr的坐标．

于是，动平台和支链之间的作用力可表示成

式中ksi为球铰链在支链坐标系Bixiyizi下相应方向上的刚度矩阵，ksi=diag(ksxi,ksyi,kszi)，详细推导过程可参考文献[3]．将式(11)代入式(15)，并将ui转换为系统坐标系BxByBzB下可得

同理，可推得第i条支链上转动副连接界面的作用力可表示为

式中r1k和r2k分别为转动副的线刚度和角刚度．

转动副的各向刚度主要由转动副轴承组件、封闭框、导轨滑块组件和丝杠组件组成，具体转动副组件受力分析可参考文献[3]．

3.2 系统总体矩阵

将弹性变形协调方程式(16)、(17)代入各子系统动力学方程式(13)，经组装并整理后可得系统静力学方程

式中：K为系统的总体刚度矩阵；U和F分别为系统的广义位移列阵和广义力列阵，分别为

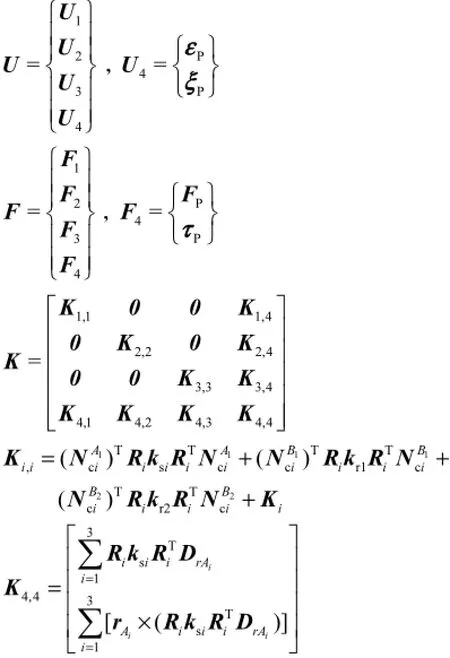
式中：4M为动平台质量矩阵；1M、2M和3M分别为伸缩支链质量矩阵，通过式(6)中rm获得．

4 算例及实验验证

A3头结构参数如表1所示，其中Pz=s+d为动平台与静平台中心距离，s=0～200 mm 为A3头全姿态沿zB向行程，θmax为动平台最大摆角．提取式(18)刚度矩阵K，通过矢量wt将其转换到动平台末端连体坐标系Atuvw进行度量．

表1 A3头结构参数Tab.1 Geometrical parameters of the A3 head

图7为Pz=550 mm、分别沿动平台连体坐标系u、v和w方向的线刚度变化趋势．从图7(a)和(b)可以看出：当动平台沿Bx轴摆动时，u方向刚度减小，v方向刚度增大；沿By轴摆动时，u方向刚度增大，v方向刚度减小，而且沿By轴摆动时，uv、两个方向的刚度呈典型的面对称分布．图7(c)显示，沿w方向的线刚度为三对称分布，在摆角较小的情况下，沿w轴方向的线刚度远大于其他两个方向．

图7 A3头线刚度分布示意Fig.7 Line stiffness distribution of the A3 head

引入质量矩阵M，在重力Fg(g=9.8 m/s2)的作用下，整机弹性变形Δ为

图8为动平台和静平台中心距分别为550mm和750mm位型时，整机在运动副自重作用下产生的弹性变形示意(变形量放大1,200倍)．当机构从位型1P运动到位型2P时，在重力作用下，整机沿By轴负方向产生弹性变形，表2中yΔ为动平台受重力作用沿By轴的弹性变形量，xθΔ为变形过程中动平台沿Bx轴的转动量．表2中数据显示，动平台沿Bz轴伸长过程中，从Pz=550 mm 位型时的57μ m增加到Pz=750 mm位型时的133 mμ，在200 mm的行程范围内变形量增幅达76 mμ．在该行程范围内，绕自身的转动变化量为0.15°．从图8可以看出，在重力作用下，支链自身的变形量相对较小，球铰链和转动副的弹性变形量相对较大．因转动副的弱刚性，在负载作用下，支链绕转动副的约束轴产生弹性变形，使得机构在BBx z平面内产生平行四边形效应，进而导致动平台在伸缩过程中产生近似平行的下垂现象．因此，在进一步设计和改进过程中，应该重点加强R副的刚度并降低动平台的自身质量．

图8 A3头在重力作用下的变形Fig.8 Diagram of A3 head deformation from gravity

表2 A3头受重力作用动平台变形量Tab.2 Moving platform deformation from gravity of the A3 head

图9为样机刚度实测图．本次实验选用螺旋千斤顶给动平台末端施加固定载荷，加载力测量装置为BK-2B压力测力仪，用来显示加载量，千分表①～⑤用来显示各测量点的变形量(μm)，其中，千分表①用来测量机构末端对应加载方向上的变形量，千分表②～⑤用来测量因基座弹性变形所引入的测试误差，在后续静刚度分析时用以消除测量误差，提高测试精度．每个位型下分别记录u方向的加载力和各测试点静态变形量，以0.5,kN为加载量，从0加载到4,kN，提取测量结果线性度较好的数据，通过直线拟合来求解整机静刚度，为消除误差，每组数据测试3次，最后取平均．

表3和表4分别为动平台沿zB轴伸出和绕yB轴转动时，沿动平台连体坐标系u方向的理论与实测刚度值．数据显示，当动平台和静平台中心距Pz增大时，沿u方向的线刚度逐渐降低．在Pz=550 mm 、θx=0°时，当θy从0°增大到30°时，u向线刚度从初始状态的7.88 N/μm增大到10.68 N/μm．其中，在摆角小于20°范围之内，仿真误差较小，当θy=30°时，误差相对较大．

图9 样机刚度实验Fig.9 Stiffness measurement setups

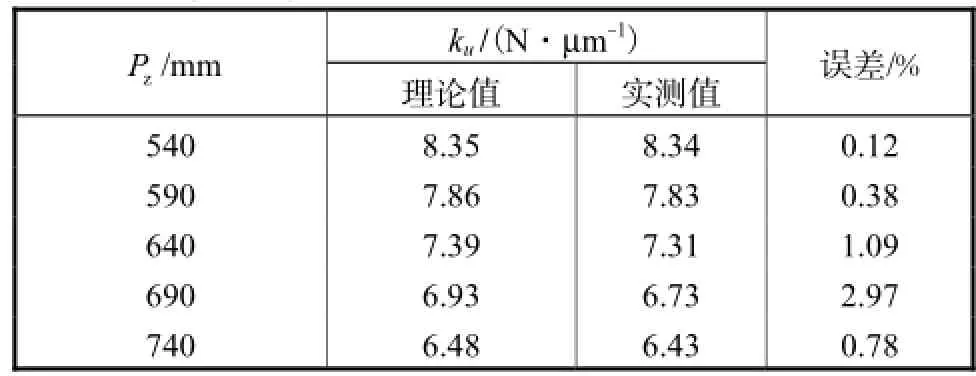
表3 A3头沿zB轴移动时u向线刚度Tab.3The u-direction stiffness of the A3 head when moving along zBaxis

表4 A3头沿yB轴转动时u向线刚度Tab.4The u-direction stiffness of the A3 head when rotating about yBaxis

可以看出，静刚度理论计算值与实测结果存在一定误差，首先是由于并联机构静刚度的变化是一个非线性过程，与机构位型有极强的相关性，导致理论计算值在姿态角较大的情况下模拟值与实测值误差较大；其次，并联机构的铰链刚度对整机静刚度影响较大，在理论计算时，各关键铰链刚度都是按理想状态处理的，3条支链所对应的铰链装配精度都一样，每条支链对应轴承和导轨的预紧力一致，所以3条RPS支链上对应的3组铰链等效刚度在理论仿真过程中均按照同样的方式等效而来，但是在原型样机中，由于制造和安装原因，各关键零部件的预紧力和装配误差均存在一定差异，而且某些部件还存在预紧力不足、铰链内部存在间隙等现象，进而导致理论计算结果与实测值存在一定误差．

但从总体来看，实测静刚度变化规律与理论仿真的变化规律一致，且仿真误差处于合理范围之内．其他方向刚度也可通过类似方法获取，本文不再一一赘述．

5 结 论

(1) 整机的主刚度随机构位姿的变化而变化，且在动平台连体坐标系下u、v方向的线刚度呈面对称分布，w方向的线刚度呈三对称分布．

(2) 在工作空间下，沿w方向的线刚度较高，远大于u、v方向的线刚度，尤其是在摆角为零的位姿下，沿w方向线刚度达到最大．

(3) 该方法可以求出整机在重力作用下的变形规律，为整机的薄弱环节分析提供新的理论依据．

(4) 本文方法求解的静刚度与实测结果相比，误差处于合理范围之内．

本文方法既可以快速预估整个工作空间中静刚度随位型的变化规律，也可以求解不同位型下运动部件自重引起的弹性变形对末端定位精度的影响；而且，在末端负载或自重作用下，本文方法不仅可以求解末端执行机构的变形量，还可以获得RPS伸缩支链各节点和铰链之间的变形量，有助于对整机各环节的柔度特性进行深入分析，为该类型机构的工程设计、改进和实际应用提供理论基础．

［1］ Caccavale F，Siciliano B，Villani L. The Tricept robot：Dynamics and impedance control[J]. IEEE/ ASME Transactions on Mechatronics，2003，8(2)：263-268.

［2］ Hennes N，Staimer D. Application of PKM in aerospace manufacturing high performance machining centers ECOSPEED，ECOSPEED-F and ECOLINER [C]// Proceedings of the 4th Chemnitz Parallel Kinematics Seminar. Chemnitz，Germany，2004：557-568.

［3］ Li Yonggang，Liu Haitao，Zhao Xueman，et al. Design of a 3-DOF PKM module for large structural component machining[J]. Mechanism and Machine Theory，2010，45(6)：941-954.

［4］ 陈 闯，王 辉，庄嘉兴. 一种新型并联动力头的前馈控制策略与实验[J]. 天津大学学报：自然科学与工程技术版，2014，47(8)：672-676. Chen Chuang，Wang Hui，Zhuang Jiaxing. Feedforward control strategy and experiment on a novel parallel spindle[J]. Journal of Tianjin University: Science and Technology，2014，47(8)：672-676(in Chinese).

［5］ Law M，Ihlenfeldt S，Wabner M，et al. Positiondependent dynamics and stability of serial-parallel kinematic machines [J]. CIRP Annals：Manufacturing Technology，2013，62(1)：375-378.

［6］ Gosselin C. Stiffness mapping for parallel manipulators [J]. IEEE Transactions on Robotics and Automation，1990，6(3)：377-382.

［7］ Majou F，Gosselin C，Wenger P，et al. Parametric stiffness analysis of the Orthoglide[J]. Mechanism and Machine Theory，2007，42(3)：296-311.

［8］ Xu Qingsong，Li Yangmin. An investigation on mobility and stiffness of a 3-DOF translational parallel manipulator via screw theory[J]. Robotics and Computer-Integrated Manufacturing，2008，24(3)：402-414.

［9］ Wang Dan，Fan Rui，Chen Wuyi. Stiffness analysis of a hexaglide parallel loading mechanism[J]. Mechanism and Machine Theory，2013，70：454-473.

［10］ Deblaise D，Hernot X，Maurine P. A systematic analytical method for PKM stiffness matrix calculation[C]//Proceedings 2006 IEEE International Conference on Robotics and Automation. Florida，USA，2006：4213-4219.

［11］ Gonçalves R S，Carvalho J C M. Stiffness analysis of parallel manipulator using matrix structural analysis[C]//Proceedings of EUCOMES 08. Germany：Springer，2009：255-262.

［12］ Wu Jun，Wang Jinsong，Wang Liping，et al. Study on the stiffness of a 5-DOF hybrid machine tool with actuation redundancy[J]. Mechanism and Machine Theory，2009，44(2)：289-305.

［13］ Heirman G，Desmet W. Interface reduction of flexible bodies for efficient modeling of body flexibility in multibody dynamics[J]. Multibody System Dynamics，2010，24(2)：219-234.

［14］ Law M，Srikantha Phani A，Altintas Y. Positiondependent multibody dynamic modeling of machine tools based on improved reduced ordermodels[J]. ASME Journal of Manufacturing Science and Engineering，2013，135(2)：021008-1-021008-11.

［15］ 宋轶民，程 航，孙 涛，等. 并联机构转动副滚动轴承静刚度参数辨识[J]. 天津大学学报：自然科学与工程技术版，2014，47(12)：1101-1108. Song Yimin，Cheng Hang，Sun Tao，et al. Static stiffness parameter identification of rolling bearings in parallel mechanisms with revolute joints[J]. Journal of Tianjin University: Science and Technology, 2014, 47(12): 1101-1108(in Chinese).

(责任编辑：金顺爱)

Static Stiffness Modeling Method of 3-RPS PKM

Luo Haiwei1，Zhang Jun2，Wang Hui1，Huang Tian1
(1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Anhui University of Technology，Ma'anshan 243032，China)

A static stiffness modeling and weight deformation solving method for a three degree of freedom(3-DOF)parallel kinematic manipulator(PKM)A3 was proposed using the substructure synthesis and static condensation technique. During the modeling process，the whole system was divided into moving platform subsystem and three identical RPS limb subsystems，in which the contributions of the joint and limb compliances to the static stiffness were considered. In the stiffness model，the sphere joint and the revolute joint were treated as lumped virtual springs with equal stiffness，the platform was treated as a rigid body，and the structural mass matrix and the stiffness matrix of the RPS limbs were established using finite element software and static condensation technique. With the compatibility conditions at interface between the limbs and the platform，an analytical governing dynamic equation of the system was then proposed. The simulation results show that the system stiffness vary with the changes of the configuration. In the coordinate system fixed to the moving platform，the distribution of the stiffness is axially symmetrical and the linear stiffness in w direction is the highest. The tip of the spindle claims a large elastic deformation due to gravity. The static stiffness simulation results are further validated by the experimental data.

static stiffness；parallel kinematic manipulator(PKM)；substructure synthesis；static condensation

TH112.5

A

0493-2137(2015)09-0797-07

10.11784/tdxbz201402014

2014-02-14；

2014-03-24.

国家高技术研究发展计划(863计划)资助项目(2012AA040702)；教育部高等学校博士点基金资助项目(20110032130006).

落海伟（1985— ），男，博士研究生，luohaiwei85@163.com.

王 辉，wanghui@tju.edu.cn.

时间：2014-04-18.

http：//www.cnki.net/kcms/doi/10.11784/tdxbz201402014.html.