用于抽水蓄能电站大坝不稳定温度场仿真的水平分区异步长解法

孙 伟，何蕴龙，王 南，熊 堃

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 长江勘测规划设计研究有限责任公司，武汉 430010)

用于抽水蓄能电站大坝不稳定温度场仿真的水平分区异步长解法

孙 伟1，何蕴龙1，王 南1，熊 堃2

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 长江勘测规划设计研究有限责任公司，武汉 430010)

对于抽水蓄能电站(PSPS)的拦河大坝上游迎水面，由于水库水位周期性升降变化，会出现与水、气等不同介质接触的交替变化现象. 将具有这种现象的迎水坝面边界称之为特殊边界. 这种交替变化的边界条件对特殊边界表面及其影响范围内的温度场分布将产生较大的影响，在温度仿真分析中不能忽略. 提出了考虑特殊边界影响的抽水蓄能电站大坝不稳定温度场水平分区异步长解法，在分析特殊边界特征的基础上，对水平分区异步长解法的基本原理进行了推导，并提出了等效放热系数的概念，从平均意义上近似考虑表面混凝土与不同介质接触时放热系数处于变化的问题，给出了水平分区界限的位置范围. 将该解法用于呼和浩特PSPS下水库拦河坝的不稳定温度场的仿真分析中. 结果表明，提出的方法是有效和省时的，并为计算更为复杂耗时的温度应力场提供了可能. 最后，对严寒地区特殊边界处可能出现的结冰与解冻问题进行了初步探讨.

抽水蓄能电站；水平分区；异步长；不稳定温度场；等效放热系数

抽水蓄能电站(pumped storage power station，PSPS)是电力系统发展到一定阶段的产物．电力系统日负荷图在每日上、下午各有一个高峰，午夜则有一个低谷．PSPS可利用夜间低谷负荷时火电站提供的剩余电能，从高程低的下水库抽水到高程高的上水库中，通过水体这一能量载体将电能转化为水的位能．在日间出现高峰负荷时，再从上水库放水发电，担任负荷图中的峰荷部分[1]．这意味着PSPS具有特殊的运行方式，在较短的周期内承担调峰填谷的任务，水库水位变幅较大．由于存在水库水位的周期性升降变化，电站的拦河大坝上游迎水面会出现与水、气等不同介质接触的交替变化现象．本文将具有这种现象的迎水坝面边界称为特殊边界．这种特殊边界的边界条件在与水接触的第1类边界条件、与大气接触的第3类边界条件、寒冷季节甚至可能与冰接触的第4类边界条件之间不断变化．特殊边界的某一点属于其中哪一类边界条件取决于该点相对水库水位的空间位置、PSPS泵站运行工况和电站运行工况的分配过程、仿真计算的时间位置以及混凝土表面水分传输机制等．由于水库水位变幅大、周期短，特殊边界所处的边界条件一直处于变动中，所引起的特殊边界表面及其影响范围内的温度变化不能忽略．

在具有特殊边界的PSPS大坝不稳定温度场的仿真分析中，由于运行周期的制约，常规水库大坝运行期较长的计算步长不再适用．一方面，具有特殊边界的这种情况与短期遭遇寒潮、昼夜温差不同，电站在工作期间，水库水位常年处于这种周期性升降的状态．计算时常年都采用短步长，大坝不稳定温度场需要求解的计算量将是巨大的，再进一步顾及到计算量更大的温度应力场，实际上是难以实现的；另一方面，这种特殊边界条件对坝体不稳定温度场的影响范围有限，对那些大部分温度变化不受特殊边界影响的地方采用短步长计算是不经济的．

常规水库大坝的温度场及温度应力场的研究[2-5]表明，由于气温和水温的年变化，运行期的温度应力仍可能引起混凝土的开裂．对于具有特殊边界的PSPS拦河大坝，气温和水温的变化周期减小，表面温度的交替变化可能会带来运行期温度应力分布特征的改变，例如在冬季，蓄水一般相当于保温，运行后伴随着水位的升降，坝面就如同短时间内在保温和没有保温之间不断循环，这自然会引起特殊的温度及温度应力分布特征．

国内外有关PSPS的这种周期短、交替变化快的特殊边界的处理，鲜见报导．文献[6]提出了高坝温度仿真分析的分区异步长解法，该方法用于解决高坝仿真分析中由于新老混凝土温度敏感性不同而建立的减小计算量的有效方法，在大坝空间域看来是一个由于浇筑时间、边界条件、内源热量变化剧烈程度等不同而建立的竖直分区异步长解法．本文借鉴分区异步长解法的思想，将其应用到考虑PSPS特殊边界影响的运行期不稳定温度场计算中．在大坝空间域上看来，这是由于受特殊边界影响程度不同而建立的水平分区异步长解法．与竖直分区异步长解法不同的是，水平分区异步长解法特殊边界处不仅接触的温度在变化，而且接触介质不同，表面的放热系数也在变化，因此本文在不稳定温度场分解过程中提出等效放热系数的概念，从平均意义上近似考虑表面混凝土与不同介质接触时放热系数也处于变化的问题．通过某PSPS的工程实例分析，将这种水平分区异步长解法的计算结果与整个坝体统一短步长解法的计算结果进行比较，证明本文解法的合理性和有效性．最后针对严寒地区PSPS寒冷季节迎水面水位升降变化过程中存在的更为特殊的结冰与解冻问题进行了初步探讨．

1 特殊边界特征分析

本节所述及的特殊边界特征的分析均针对普通常温地区PSPS而言，特殊边界只可能是水边界或气边界，而不涉及大坝上游迎水面的结冰与解冻的问题.有关冰层覆盖与融化的问题将在第4节进行探讨.

PSPS拦河大坝特殊边界特征分析如图1所示.设点A1为大坝坝面特殊边界上任一点，点A1距离死水位高度为H，正常蓄水位与死水位高度差为H′. 下面从两个方面研究点A的边界特征．

1)点A1为水边界或气边界的条件

水库水位高程和干湿交替变化条件下混凝土(或混凝土表面附着的永久保温材料)表层水分的传输机制决定了点A1的边界类型．

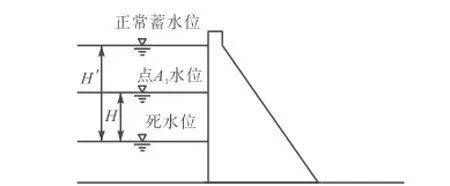
图1 PSPS拦河大坝特殊边界特征分析Fig.1 Analysis of the characteristics of special boundary of PSPS dam

水库水位高程的变化与PSPS的泵站运行工况和电站运行工况的分配过程有关．不失一般性，将PSPS运行周期(1,d)分为4个时段：①下水库抽水时段(零时至凌晨T1时)；②下水库低水位时段(凌晨T1时至下午T2时)；③下水库蓄水时段(下午T2时至晚间T3时)；④下水库高水位时段(晚间T3时至24时) ．水库的水位-时间曲线如图2所示．

图2 水库的水位-时间曲线Fig.2 Curve of water level-time of reservoir

干湿交替条件下混凝土表层水分的传输机制属于混凝土湿度场的研究范畴．Bazant等[7]在1972年以混凝土内部相对湿度为基本变量，用扩散方程的形式描述混凝土在干燥过程中内部相对湿度的变化，即

式中：H为混凝土相对湿度；t为时间；DH(H)为随H变化的扩散系数．式(1)为一个非线性方程，需迭代求解．利用该扩散方程，在给定的初始湿度和边界湿度条件下，可求出混凝土多孔介质的湿度场分布．然而，一方面DH(H)与温度、混凝土组成材料、配合比(特别是水胶比)、开裂情况、应力状况等均有关系，加上坝体施工期永久保温材料(蓄水后运行期可能处于部分失效状态)的影响，故难以准确确定；另一方面，湿度场、温度场相互影响，两者的耦合计算更加大了特殊边界条件下的非稳定温度场的计算难度，不便应用于实际工程．

文献[8]对混凝土近表面层一维水分传输问题进行了实验研究．结果表明：升温干燥时，水分传输的近表面层厚度很小，近表面水蒸气含量梯度很快消失；等温吸湿时，近表面不存在明显的湿度梯度．基于此，为了便于工程应用，本文采用以下简单原则确定点A1的水气边界条件：①忽略水库水位上升过程中吸湿过程的湿度梯度，认为点A1在水位高程以下，则视为水边界；②忽略水位下降中干燥过程的水蒸气含量梯度，认为点A1在水位高程以上，则视为气边界.

综上所述，可得如下结论：①点A1在水位高程以下，则视为水边界，边界温度等于相应时刻的水温；②点A1在水位高程以上，则视为气边界，边界温度等于相应时刻气温．

2)在一个运行周期里，点A1为水边界或气边界的时段分配

在PSPS一个运行周期1,d里，点A1(距离死水位高度为H)为水边界的时间为1t，为气边界的时间为．以下讨论t1、t2是如何分配的．假设在下水库抽水及蓄水过程中，水位均匀变动．水边界和气边界时段分配如图3所示．

图3中，1M、2M为以点A1处的水位H做平行于时间轴的直线与水库水位-时间曲线的两个交点的时间坐标，即点A1在0～1M和2M～24为水边界，在

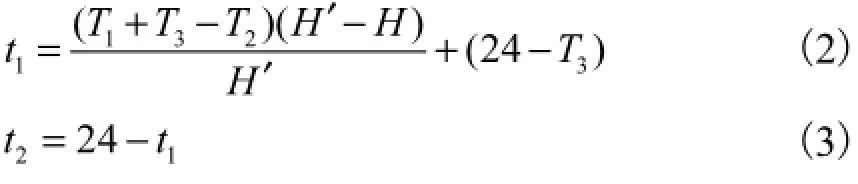
图3 水边界和气边界时段分配Fig.3 Allocation of the period of water and gas boundary

2 水平分区异步长解法基本原理

2.1 公式推导

水平分区异步长解法如图4所示．特殊边界影响区记为R1，非影响区记为R2，特殊边界记为S，其余常规水边界、气边界分别记为S1～S4，影响区和非影响区接触面记为B1．周围介质温度分别为：死水位以下S1边界水温w1T，S2、S3边界气温gT，尾水位以下S4边界水温w2T，特殊边界S温度f(t)．蓄水后运行期混凝土水化热温升的影响已不必考虑．图4中，点A～E(影响区上游点A、影响区内部点B、分区界限位置点C、非影响区内部点D、非影响区下游点E)是为了便于分析而取出的典型点．

2.1.1 总温度场——T场

T场应满足下列条件．

(1) 在影响区域R1内热传导方程为

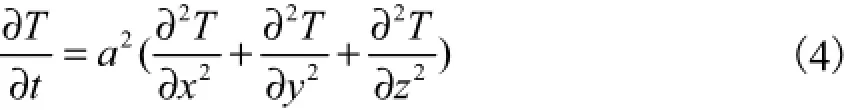
式中：T为总温度场；a为导温系数．

式(4)的初始条件为

式(4)的边界条件为

式中：λ为导热系数；wβ为大坝混凝土与水接触时的表面放热系数；gβ为大坝混凝土与空气接触时的表面放热系数．

式(4)的特殊边界条件为

式中：β为特殊边界处大坝混凝土与介质接触时的表面放热系数．当与不同介质接触时，β值不同．

(2) 在接触面上温度满足

式中1T、2T为接触面两侧的温度．

(3) 在非影响区域R2内热传导方程为

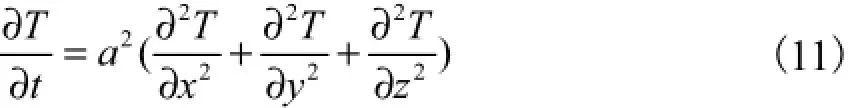
式(11)的初始条件为

由于待求解的热传导方程(4)、(11)是线性的，故可将总温度场T进行分解，即

2.1.2 分解温度场—U场

分解的温度场—U场应满足下列条件．

(1) 在影响区域R1内热传导方程为

式(16)的初始条件为

式(16)的边界条件为

式(16)的特殊边界条件为

式中(x, y, z)∈ΓS．

(2) 在接触面上温度满足

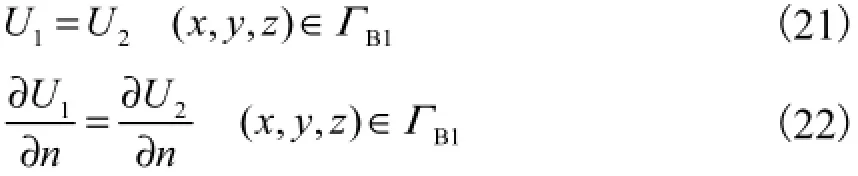
(3) 在非影响区域R2内热传导方程为

式(23)的初始条件为

式(23)的边界条件为

2.1.3 分解温度场—V场

分解的温度场—V场应满足下列条件．

(1) 在影响区域R1内热传导方程为

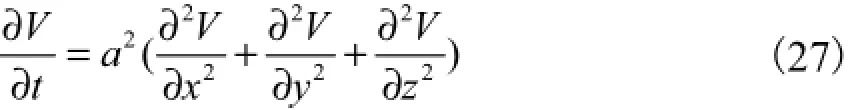
式(27)的初始条件为

式(27)的边界条件为

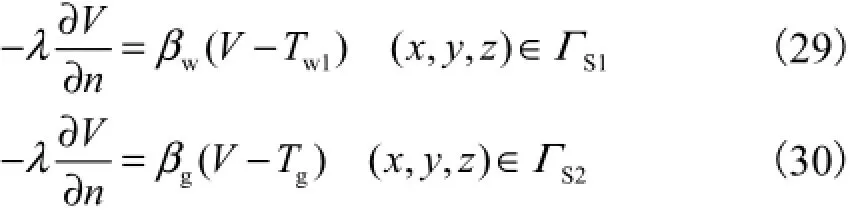
式(27)的特殊边界条件为

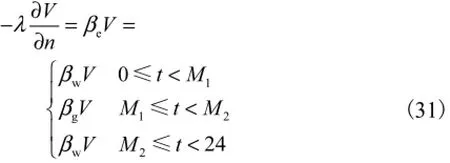
式中：(x, y, z)∈ΓS；βe为等效放热系数，具体分析见第2.2节．

在接触面上满足

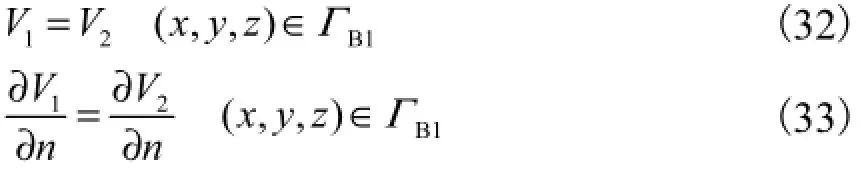
在非影响区域R2内热传导方程为

式(34)的初始条件为

式(34)的边界条件为

由于待求解的热传导方程都是线性的，上述分解是严格的．

在U场中，温度场的剧烈变化主要局限于影响区域R1，在影响区域R1与非影响区域R2的接触面B1上，其影响已趋于0，即U1=U2=0，x∈ΓB1．非影响区域R2满足下列条件：

热传导方程为

初始条件为

边界条件为

显然，满足式(38)～式(42)的解为：在非影响区域R2中0U=．

因此，U场只需要在影响区域R1中求解．由于U场中特殊边界条件随时间而急剧变化，故计算中需要采用较小的时间步长1τΔ．V场在全区域R1＋R2内求解，因其变化平缓，计算中采用较大的时间步长2τΔ．总温度场的分解如表1所示．

需要说明的是，在取时间步长时需要注意，1τΔ和2τΔ是有关联的，2τΔ必须为n个1τΔ的代数和．本文取1=1hτΔ，2=1dτΔ．

在接触面上有

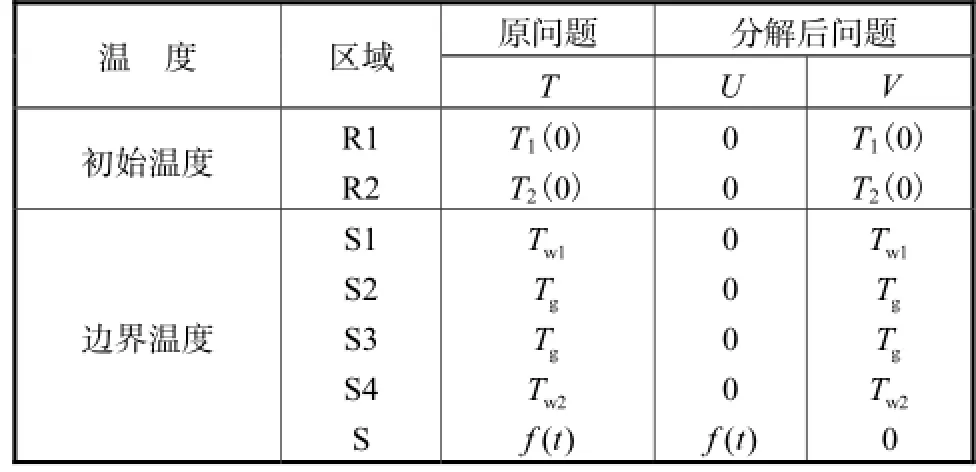
表1 总温度场的分解Tab.1 Decomposition of total temperature field

水平分区异步长解法的求解步骤为：①求解U场，求解域为影响区域R1，时间步长为1,h；②求解V场，求解域为影响区域R1和非影响区域R2，时间步长为1,d；③将U场24,h末时刻的计算结果与V场1,d末时刻的计算结果相叠加，即得到最终T场1,d的分布．在实际工程中，叠加过程可以通过外部程序调用有限元软件自动连续地加以实现．

2.2 等效放热系数

水平分区异步长解法与文献[6]中竖直向分区异步长解法不同之处在于，这种特殊边界处不仅接触的温度在变化，而且由于接触介质不同，其表面放热系数也在变化．在进行U场小步长计算时，可以随着接触介质的变化设定相应的表面放热系数，而在V场长步长计算时，一个长步长中已经包含了与不同介质接触的变化过程，因此需要设定一个合理的等效放热系数，从平均意义上近似考虑表面混凝土与不同介质接触时的放热系数处于变化的问题．

与第1节研究方法相同，仍假设点A为水边界的时间为t1，为气边界的时间为t2，t1+t2=24 h ．

V场的特殊边界处混凝土表面传递的总热量为

式中：wQ为混凝土与水接触时，混凝土表面传递的热量；gQ为混凝土与空气接触时，混凝土表面传递的热量；aV为混凝土与水接触时的表面温度；bV为混凝土与空气接触时的表面温度．

此时边界温度无论是水温还是气温，均保持不变．在气边界时，相当于空气温度变化非常缓慢，周期趋于无限大，虚拟厚度的影响可以忽略(实际上，变化周期为年的时候可以忽略[2])，可按第1类边界条件近似处理，即假设Vb≈Va(如此假设是由于βw远大于βg(βw≈320βg)，而且特殊边界附近交替变化的温度已经在U场得到反映，特殊边界附近U场占T场的比例很大，所以V场的近似处理所带来的影响也会较小，因此取Vb≈Va影响也将不大) ．此时有

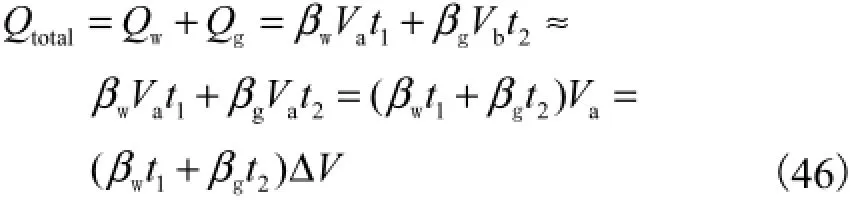
式中ΔV为V场中坝面混凝土表面温度与外界水温之差，ΔV=Va．

将总热量Qtotal表示成热流量与时间的乘积，式(46)可写成

由式(47)有 e

β即为具有平均意义的特殊边界等效放热系数.

特殊边界范围内，位于不同高程的点，与水、气接触的时间长短不同(具体接触时间的分析见第1节)，因而其等效放热系数也不同．为了提高精度，需将特殊边界按浇筑层细分，根据每一层的水、气接触时间计算式(2)～(3)和等效放热系数计算式(49)，求得每一层的等效放热系数值．

2.3 分区位置的合理确定

在离特殊边界较远处，特殊边界处交替的温度变化对不稳定温度场的影响很小．取某个很小的温度影响值ε0作为判别标准，对于温度影响值ε＜ε0的部分，特殊边界对其影响可忽略不计，以此可以确定特殊边界的影响深度．

在以下的分析中，取温度影响值ε0=0.01℃．影响深度d的确定可通过理论计算确定．

热传导方程为

初始条件为

边界条件为

式中：P为温度变化周期；B为表面温度变幅．

拉普拉斯变换得到满足上述条件的解为

对于气边界，考虑到虚拟厚度，g(,)T x t=因此气温边界的影响衰减得更快，影响深度比水温边界小．

对于这种周期短、变幅大的温度变化，应取较小的周期P．取温度变化周期为1,d，t以1,h为单位步长，计算得到水温边界的影响深度如表2所示．

表2 水温边界影响深度Tab.2 Influence depth of the water temperature boundary

取B＝20,℃，影响深度d＝1.36,m处温度影响值满足ε＜ε0．结合网格划分及分区方便等因素，选定分区界限位置范围为特殊边界表面附近2～3,m．

3 工程实例分析

以呼和浩特PSPS为例，将考虑特殊边界影响的水平分区异步长解法应用于其下水库拦河坝的不稳定温度场的仿真分析中．该电站为国内第1例位于严寒地区的PSPS，位于内蒙古自治区呼和浩特市东北的大青山脉中麓哈拉沁沟下游，距呼和浩特市中心公路里程约20,km．下水库库区所在流域属于中温带季风亚干旱气候区，具有冬长夏短、寒暑变化急剧的特征．冬季长达5个月，漫长而严寒．

呼和浩特PSPS一般从凌晨零时开始到凌晨7时从下水库抽水至上水库，调峰发电泄水主要是在16：00—20：00，下水库库盆内水位在死水位(1,355.00,m)到正常蓄水位(1,400.00,m)之间变化，昼夜升降变幅为45,m，水位变幅大，周期短．

选取呼和浩特PSPS下水库拦河坝为研究对象，验证水平分区异步长算法有效性．大坝采用“金包银”形式，即坝体上游侧包有厚2～3,m的常态混凝土．为简单起见，将影响区域R1和非影响区域R2的接触面划分在上游常态混凝土与碾压混凝土交界面处，即B1取为上游常态混凝土与碾压混凝土分界线，影响区域R1和非影响区域R2范围见图4．

设计算例1 计算时间取运行期夏季6月．以施工期及运行期蓄水开始至电站以抽水蓄能方式运行稳定的温度分布为初始条件．为反映特殊边界处温度变化是由于其与水温和气温交替接触所引起，而排除昼夜温差等其他因素的影响，假设在此短时间(3,d)内，水温和气温不变．根据文献[9]分析结果，水温取为定值17.0,℃，气温取为定值19.5,℃．采用两种解法对比分析．解法1精确模拟一天内水库实际变化过程，时间步长均匀为1,h，时长为72,h(以下简称整个坝体统一短步长解法，记为0T场)，计算结果为每天24,h末时刻温度值．解法2采用水平分区异步长解法，即：①求解U场，求解域为影响区域R1，时间步长为1,h，时长为24,h；②求解V场，求解域为影响区域R1＋非影响区域R2，时间步长为1,d；③取U场24,h末时刻温度计算结果与V场第1天末时刻的计算结果相叠加，得到最终第1天的T场．重复操作①、②、③，共计算3,d．计算结果为U场24,h末时刻与V场第1天末时刻计算结果叠加的温度．

取1,377,m高程点A～E(见图4)，算例1两种解法典型点温度值对比见表3．两种解法坝体不稳定温度场分布对比见图5．

表3 算例1两种解法典型点温度值对比Tab.3 Comparison of temperature value of typical points under two algorithms in example 1, ℃

图5 算例1两种解法坝体不稳定温度场分布对比(单位：℃)Fig.5Comparison of the unsteady temperature filed of the dam under two algorithms in example 1(unit：℃)

分析相应的图表，可得到以下结论．

(1) 从特殊边界表面到分区界限处，U场越来越小，而V场越来越大，即特殊边界附近U场占T场的比例较大，V场中采用等效放热系数的近似处理引起的误差较小，不超过0.15,℃．

(2) 总体上来说，采用水平分区异步长解法与整个坝体统一短步长解法在同一时刻大坝不稳定温度场分布十分接近，非影响区域R2温度分布吻合较好，影响区域R1则在上游边界和分区界限位置处由于V场的简化处理存在误差，但温度差值不超过0.15,℃．

(3) 解法1时间步长均匀为1,h，时长为72,h，在此期间，大坝上游面不稳定温度场变化不大，变幅为0.55,℃，最大值约为18.30,℃，出现在表面特殊边界处1,360,m高程附近．而解法2只得到了3,d中3个时刻(24 ht=，48 h，72 h)的计算结果，大坝上游面不稳定温度场变幅为0.35,℃，最大值约为18.05,℃，变幅和最大值均较解法1小，原因是解法2每天的温度分布是由U场24,h末时刻温度计算结果与V场该天末时刻的计算结果相叠加得到的，因此只能反映周期为1,d的温度变幅和最大值．通常来说，运行期不稳定温度场仿真分析通常以1,d(甚至更大)为计算步长，关注周期为1,d的温度变幅和最大值已经足够满足工程分析的需要．因此，水平分区异步长解法在温度变幅和最大值方面虽有误差，但能够满足分析的需要．

(4) 水平分区异步长解法只需要在特殊边界影响的较小范围内采用短步长计算剧烈变化的U场，因而比整个坝体统一短步长解法节约计算时间．同时，采用该算法，先假定影响区与非影响区的分界面暂时固定，各个区按不同的时间步长分别计算，然后再放松分界面的约束，可实现应力场的简化计算，即水平分区异步长解法为复杂耗时的PSPS拦河大坝蓄水后正常运行期温度应力场的计算提供了可能．

(5) 由以上分析可知，本文提出的考虑特殊边界影响的PSPS大坝不稳定温度场水平分区异步长解法是合理有效．

4 严寒地区特殊问题初探

如果外界气温过低，残余水分长时间暴露在空气中会结冰，水位回升后，冰层浸泡在水中又会解冻．比如第3节中位于高寒地区的呼和浩特PSPS，冬季长达5个月，11月、12月、1月、2月的月平均气温均低于0,℃，1月则达到-12.2,℃，因此其特殊边界迎水面存在结冰与解冻的问题．

由于国内同类型工程较少，故目前对迎水面结冰与解冻问题认识不足．位于俄罗斯莫斯科的扎戈尔PSPS同样地处高寒地区，它的研究结论可为严寒地区PSPS混凝土表面结冰与解冻的问题提供参考．

扎戈尔PSPS[10-11]位于俄罗斯莫斯科东北角的谢尔捷耶夫-波萨德斯克地区的库尼亚河上，位于高寒地区．扎戈尔抽水蓄能电站上水库护坡混凝土板工作温度状态[12]如表4所示．当水库水位下降时，脱离水面而暴露在空气中的护坡混凝土，在－10～0,℃的空气中暴露时间超过3.5,h就会结冰，而要将该冰层融化则需要在水中浸泡4,h，循环时间不小于7.5,h．

类比分析作为本文工程实例的呼和浩特PSPS，考虑其坝址处气温分布规律及水库运行特性，可得出以下类比结论：①呼和浩特PSPS下水库在11月、12月、1月、2月4个月份运行时，迎水面在空气中暴露不少于3.5,h就会结冰；②一个周期内，水、气交替区至少浸水4,h，迎水面冰层会融化．

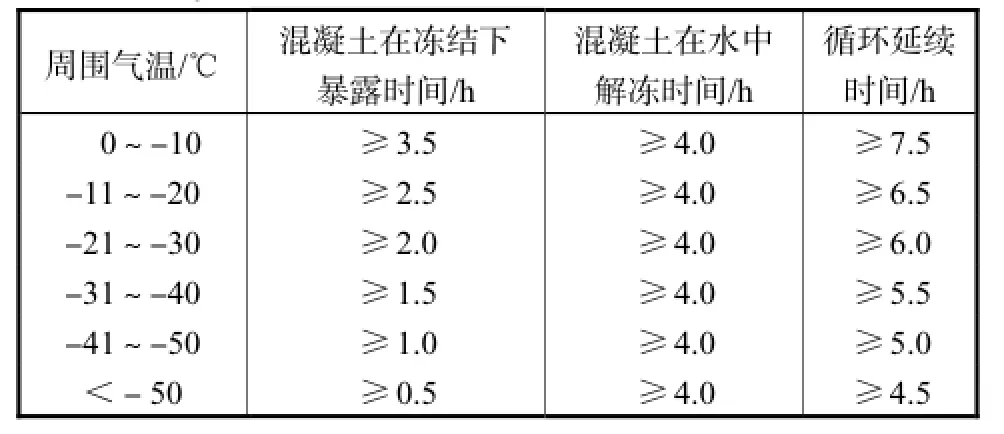
表4 迎水面混凝土结冰与解冻规律Tab.4Rule of freezing and thawing of upstream boundary concrete

另外，扎戈尔PSPS上水库护坡混凝土板温度状态的研究表明，冰下的混凝土温度在-2～0,℃之间，如图6所示．结冰对混凝土坝面是有利的，因为冰层起到了一定的保温效果．为了简单起见，结冰后的边界温度视为0,℃．

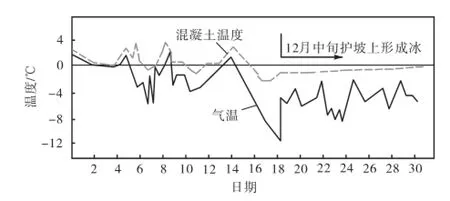
图6 结冰后混凝土表面温度分布(12月)Fig.6Temperature distribution of concrete surface after freezing (December)

现在来回答与第1节相同的两个问题．

1) 点A为水边界或气边界的条件

对于严寒地区冬季月平均气温小于0,℃的月份，按照以下原则近似确定边界条件：①若点A在下水库水位以上，在0～3.5,h内，附着有残余水分，仍视为水边界；在3.5,h以上，点A残余水分已结冰，则点A边界温度按0,℃处理．②若点A在下水库水位以下，在0～4,h内，附着的残余水分结冰没有解冻，则点A边界温度仍按0,℃处理；在4,h以上，结冰已解冻，则视为水边界．

2) 在一个运行周期里，点A为水边界或气边界的时段的分配

在抽水蓄能电站一个运行周期1,d里，令点A为水边界的时段为1t，与冰接触(称之为冰边界)时段为．假设在下水库抽水及蓄水过程中，水位均匀变动．水边界和冰边界时段分布如图7所示，则有

寒冷季节冰边界，因为考虑到冰层的保护作用大坝混凝土表面温度近似取0,℃，相当于忽略混凝土与冰层之间的热阻，与冰接触的放热系数可取代入式(49)得到等效放热系数

仍以呼和浩特PSPS下水库拦河坝为例，验证水平分区异步长算法对于寒冷地区结冰与解冻特殊问题的适用性．

设计算例2 计算时间取为运行期冬季12月，其他条件与算例1相同．算例2两种解法坝体不稳定温度场分布对比如图8所示．

分析相关计算成果，可得到以下结论．

(1) 总体上来说，对此严寒地区寒冷季节的大坝采用水平分区异步长解法，与整个坝体统一短步长解法在同一时刻大坝不稳定温度场分布十分接近，非影响区域R2温度分布吻合较好，影响区域R1则在上游边界和分区界限位置处由于V场的简化处理存在误差，但温度差值不超过0.05,℃．

(2) 呼和浩特PSPS下水库库容小，进出水口相对当地库底高程仅为5,m，电站装机容量、出入库流量大，因此认为电站运行方式引起的水体掺混作用足以使整个水域温度分布均匀，不存在竖直高程上的梯度，因此12月整个水域均取为0,℃[9]，加上结冰后边界温度也视为0,℃，因此U场温度分布梯度小，较为均匀，且U场占T场比例不大．对于其他库容大、进出水口高程高的严寒地区PSPS水库，水温在库表和库底高程之间存在分布梯度，此时U场分布不再均匀，具有算例1中“从特殊边界表面到分区界限处，U场越来越小，而V场越来越大，特殊边界附近U场占T场的比例较大”的特点．

(3) 两种解法计算结果对比表明，基于对结冰与解冻问题的这种近似处理原则，本文提出的考虑特殊边界影响的PSPS大坝不稳定温度场水平分区异步长解法对于寒冷地区结冰与解冻特殊问题也适用．

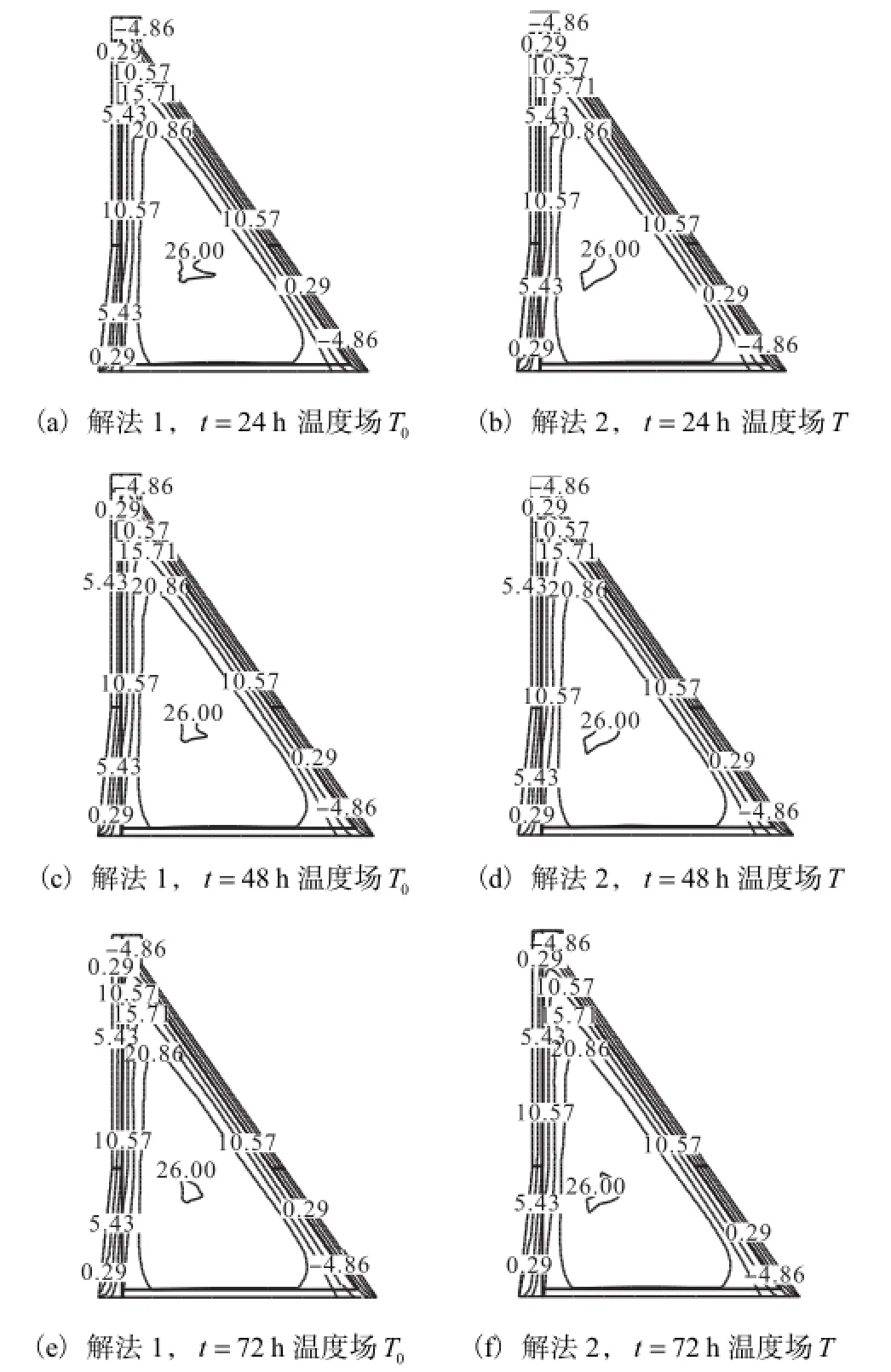
图8 算例2两种解法坝体不稳定温度场分布对比(单位：℃)Fig.8Comparison of unsteady temperature filed of the dam under two algorithms in example 2(unit：℃)

5 结 论

(1) 本文提出了考虑特殊边界影响的PSPS大坝不稳定温度场水平分区异步长解法，并在不稳定温度场分解过程中提出了等效放热系数的概念，并通过理论计算，确定分区界限位置范围大致为特殊边界表面附近2～3,m．

(2) 对呼和浩特PSPS的工程实例进行了分析，将这种水平分区异步长解法的计算结果与整个坝体统一短步长解法计算结果进行了比较，二者的影响区域和非影响区域的不稳定温度场分布均十分接近，证明本文提出的算法是合理有效的．

(3) 水平分区异步长解法比整个坝体统一短步长解法节约了计算时间．同时，也为具有特殊边界的PSPS拦河大坝蓄水后正常运行期温度应力场的计算提供了可能．具有特殊边界的PSPS拦河大坝蓄水后正常运行期温度应力场的计算今后有待研究．

(4) 水平分区异步长解法在建模与求解过程中需要注意：分区界限位置既需要足够大，以满足U场和V场分开计算的要求，又希望尽量小，以节省计算资源，文中经过理论推导给出了大致的范围，可供参考；为了提高精度，需将特殊边界按浇筑层细分，根据每一层的水、气接触时间，求得每一层的等效放热系数值；总温度场分解后得到的U场和V场，初始条件和边界条件有很大的不同，求解过程需要加以注意；叠加过程可以通过外部程序调用有限元软件自动连续的加以实现；初步计算时可与文中算例一样，选用几天，采用本文解法与整个坝体统一短步长解法进行比较验证，以检查或调整计算模型．

(5) 本文在处理特殊边界与水、气交替接触时，对混凝土表面水分传输以及寒冷季节迎水面结冰与解冻问题进行了一定程度上的近似处理．笔者认为需要在以后有关实验或者工程经验更加丰富时，对此近似处理进行验证或改进(如考虑表层水分传输机制、进行湿度场和温度场耦合计算等)，使得仿真条件更加接近真实情况．

［1］ 陆佑楣，潘家铮. 抽水蓄能电站[M]. 北京：水利电力出版社，1992. Lu Youmei，Pan Jiazheng. Pumped Storage Power Station[M]. Beijing：Water Resources and Electric Power Press，1992(in Chinese).

［2］ 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京：中国电力出版社，1999. Zhu Bofang. Thermal Stresses and Temperature Control of Mass Concrete[M]. Beijing：China Electric Power Press，1999(in Chinese).

［3］ 郭之章，傅 华. 水工建筑物的温度控制[M]. 北京：水利电力出版社，1990. Guo Zhizhang，Fu Hua. Temperature Control of Hydraulic Structure[M]. Beijing：Water Resources and Electric Power Press，1990(in Chinese).

［4］ 李松辉，张湘涛，张国新，等. 高混凝土重力坝关键部位温控防裂研究[J]. 水力发电学报，2013，32(3)：182-186. Li Songhui，Zhang Xiangtao，Zhang Guoxin，et al. study on temperature control for key components of high concrete dam[J]. Journal of Hydroelectric Engineering，2013，32(3)：182-186(in Chinese).

［5］ 李守义，赵基花. 碾压混凝土重力坝温度场与温度徐变应力仿真分析[J]. 西安理工大学学报，2004，20(1)：58-62. Li Shouyi，Zhao Jihua. Simulation analysis of temperature field and thermal stress of RCC gravity dam[J]. Journal of Xi’an University of Technology，2004，20(1)：58-62(in Chinese).

［6］ 朱伯芳. 不稳定温度场数值分析的分区异步长解法[J]. 水利学报，1995(8)：46-52. Zhu Bofang. A method using different time increments in different regions for solving unsteady temperature filed by numerical method[J]. Journal of Hydraulic Engineering，1995(8)：46-52(in Chinese).

［7］ Bazant Z P，Najjar L J. Nonlinear water diffusion in nonsaturated concrete[J]. Materials and Structures/Materiauxet Constructions，1972，5(25)：3-20.

［8］ 李春秋. 干湿交替下表层混凝土中水分与离子传输过程研究[D]. 北京：清华大学土木水利学院，2009. Li Chunqiu. Study on Water and Ionic Transport Processes in Cover Concrete Under Drying-Wetting Cycles[D]. Beijing：School of Civil Engineering，Tsinghua University，2009(in Chinese).

［9］ 孙 伟，何蕴龙，赵 鑫，等. 抽水蓄能电站水库水温简化模型与应用[J]. 武汉大学学报：工学版，2013，46(4)：449-457. Sun Wei，He Yunlong，Zhao Xin，et al. A simplified method of reservoir water temperature for pumped storage power station and its application[J]. Engineering Journal of Wuhan University，2013，46(4)：449-457(in Chinese).

［10］ 库列绍夫A II. 扎戈尔抽水蓄能电站的问题及解决办法[J]. 刘正启，译. 水利水电快报，2001，22(12)：14-15. Kuleshov A II. Problems and solutions in Zhageer pumped storage power station[J]. Liu Zhengqi，Trans. Water Conservancy and Hydropower Express，2001，22(12)：14-15(in Chinese).

［11］ 库德林B II. 扎戈尔抽水蓄能电站专项工程施工[J].赵秋云，译. 水利水电快报，2000，21(15)：10-14. Kudrin B II. The special engineering construction in Zhageer pumped storage power station[J]. Zhao Qiuyun，Trans. Water Conservancy and Hydropower Express，2000，21(15)：10-14(in Chinese).

［12］ 夏尔库诺夫С В. 扎戈尔抽水蓄能电站上库护坡混凝土板工作温度状态的研究[J]. 刘正启，译. 水利水电快报，2002，23(12)：17-19. Charles Kuno С В. Study on the working temperature state of concrete plate in the upper reservoir protection slope in Zhageer pumped storage power station[J]. Liu Zhengqi，Trans. Water Conservancy and Hydropower Express，2002，23(12)：17-19(in Chinese).

(责任编辑：樊素英)

A Method Using Different Time Steps in Different Horizontal Regions for Simulation of Unsteady Temperature Field of Pumped Storage Power Station Dam

Sun Wei1，He Yunlong1，Wang Nan1，Xiong Kun2
(1. State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China；2. Changjiang Survey Planning Design and Research Limited Liability Company，Wuhan 430010，China)

Because of the cyclical fluctuation of the water level of the reservoir，the upstream boundary of the pumped storage power station(PSPS)dam would encounter alternate contact with water，gas and other different media. The upstream dam boundary with this kind of characteristics is called the special boundary. These alternating boundary conditions have a big impact on the distribution of the temperature field of special boundary surface and its impact range，and cannot be ignored in the temperature simulation analysis. This paper proposes a method of solving unsteady temperature field of pumped storage power station dam with different time steps in different horizontal regions，and analyzes in detail the characteristics of special boundary and gives the formula derivation of the basic principle of the method with different time steps in different horizontal regions. The concept of equivalent heat transfer coefficient is also put forward to averagely and approximately consider the variation of heat transfer coefficient when the surface concrete contacting with different media and the position of horizontal partitioning boundary is given as well. The method is used in the simulation analysis of unsteady temperature field of Hohhot PSPS reservoir dam. The results show that the proposed method is effective and provides the possibility of calculating the temperature stress field which is more complex and time-consuming. Finally，the paper tentatively discusses the problem of freezing andthawing at the special boundary in cold regions.

pumped storage power station；horizontal partition；different time steps；unsteady temperature field；equivalent heat transfer coefficient

TV697.2

A

0493-2137(2015)09-0817-10

10.11784/tdxbz201401032

2014-01-11；

2014-06-18.

中国博士后科学基金资助项目(2012M511594)；国家大坝安全工程技术研究中心开放基金资助项目(NDSKFJJ1103).

孙 伟（1990— ），男，博士研究生，sunweimoving@126.com.

何蕴龙，ylhe2002@aliyun.com.cn.