甲型H1N1流感病毒感染与性别关系的统计分析

朱永生 梁学友 钟 山 胡俊▲

1.云南农业大学基础与信息工程学院，云南昆明 650201；2.西南大学附中，重庆 400700

人群对甲型H1N1流感病毒普遍容易感染，2009年北美各国相继暴发了新甲型H1N1流感病毒感染病例，在几个月时间里蔓延全球遍布200多个国家[1]。由于甲流病毒极易传染的特性，导致甲流发展迅速，严重危害人的身体健康。但针对甲型H1N1病毒的流行病特点和甲流疫苗的研制成功，采取隔离传染源、保护健康人群、接种疫苗的综合性积极预防措施，甲流疫情得到得到有效控制。2014年1月份北京市出现首例因感染甲型H1N1死亡的病例，说明对甲流的研究不能因为流行期的过去而终止，因此有很多专家学者对其各方面进行了研究[2-5]。

根据北京市2009年数据显示，北京市有7259例确诊为甲型H1N1流感，其中男性患者的比例为4361/7259=60%，女性患者的比例为40%。北京市总人口数为17 550 000人，其中男性所占比例为51.1%，仅比女性所占的比例48.9%稍高一些。然而在感染甲流的人中，男性患者所占比例远高于女性患者。本研究对北京市截至到2009年11月1日，全市报告甲型H1N1流感确诊病例数据建立一个列联表，采用x2检验和似然比检验法来检验北京市人口中男性与女性感染甲型H1N1流感病毒的概率是否显著不同。

1 资料与方法

1.1 一般资料

数据来自北京卫生信息网疫情周报（2009年10月26日～11月1日）[6]以及2010年北京统计年鉴。2009年截至第43周北京市累计报告甲型H1N1流感确诊病例7259例（男4361例，女2898例）。北京全市人口中，男为896.2万人，占总人口的51.1%；女为858.8万人，占总人口的48.9%。性别比（以女性为100，男性对女性的比例）为104.1。经过整理后的数据如下，表1为甲型H1N1流感感染人数的四格表。

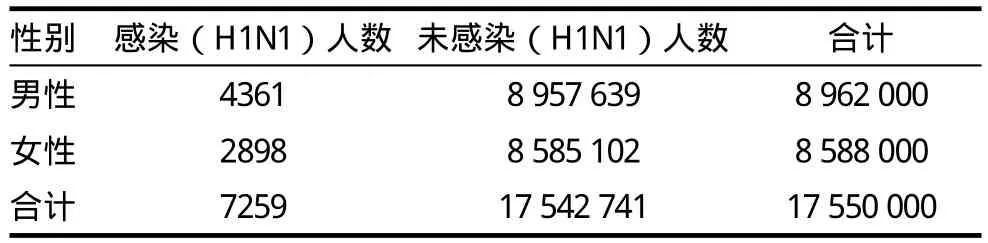
表1 甲型H1N1流感感染人数

1.2 方法

1.2.1 x2检验[7]一般总体中的个体可按两个属性A与B分类，A有r个类A1……Ar，B有c个类A1……Ac，从总体中抽取大小为n的样本，设其中有nij个个体既属于Ai又属于Bj，nij成为频数，将r×c个nij排列为一个r行c列的二维列联表。

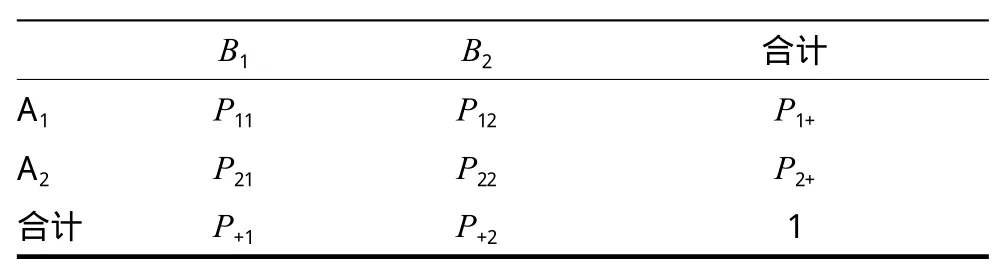
表2 概率四格表

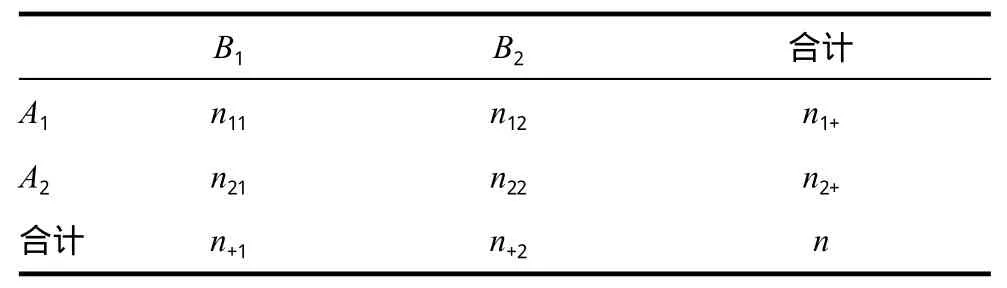
表3 频数四格表

我们用属性A表示性别，它有两个水平：A1表示男性和A2表示女性，属性B表示是否感染甲流，它也有两个水平：B1表示感染甲流和B2表示未感染甲流。考虑概率四格表（表2）和与其对应频数四格表（表3）当P1=P2时，属性A和属性B相互独立，其中 P1=P（B1/A1），P2=P（B1/A2）。

首先建立假设H0：甲流感染与性别无关，即A与B是独立的。

H0∶ Pij=Pi+P+j，i=1,2,j=1,2；H1：存在 i与 j，使得Pij≠Pi+P+j

表3中的n11为实际频数，表2的P11为A1∩B1的概率，因而nP11为理论频数，Pij是在r- 1成立时得到的 Pij的最大似然估计，

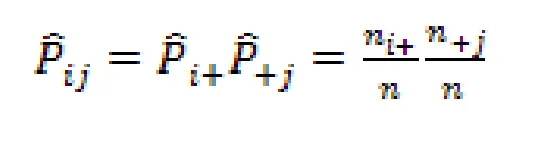
由Pearson的x2定理[8]，有检验统计量

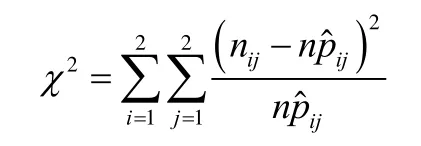
在原假设 H0成立时，上式服从自由度为：

rc-(r+ c- 2 )-1 = (r- 1 )(c- 1 ) = ( 2- 1)´ ( 2- 1 )= 1 的 x2分布。对于给定的显著水平 a (0 a1)，检验的拒绝域

1.2.2 似然比检验[7-10]在四格表中带参数的分类数据的似然比检验统计量为

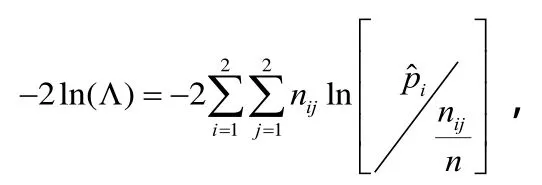
由上所述，P11的极大似然估计为

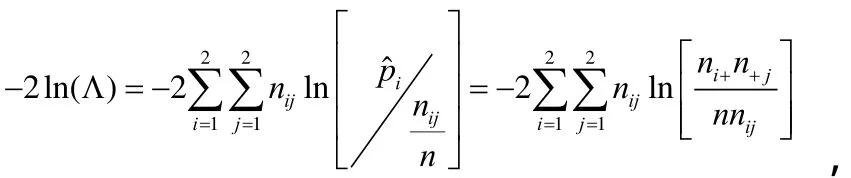
统计量的渐近分布也是x2（1）分布。显著水平为 α 的检验的拒绝域为

2 结果

2.1 x2检验结果

经计算x2检验统计量的观测值为236.004[11-12]，当显著水平α=0.05时， ，因而在显著水平α=0.05时应拒绝原假设H0，接受H1，即甲流病毒感染与性别有关系。

由于此分布是一个连续分布，而四格表资料属于离散型分布，由此计算得来的统计量的抽样分布亦呈离散性质，为了改善统计量分布的连续性，需要对统计量进行连续性校正，则连续校正的x2检在显著水平α=0.05时应拒绝原假设H0，接受H1，也同样可以得出甲流病毒的感染与性别有关系。

2.2 似然比检验的结果

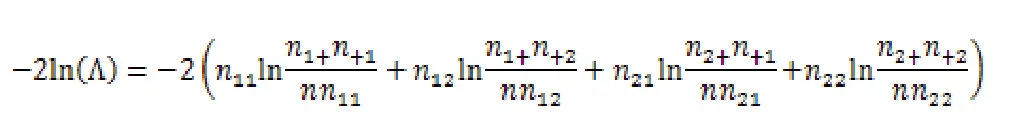
其观测值为237.917，在显著水平α=0.05时应拒绝原假设H0，接受H1，所得出结论也是甲流病毒的感染与性别有关系。

3 讨论

通过Pearson x2检验和似然比检验，结果均为拒绝原假设，即认为男性感染H1N1流感病毒的概率不等于女性感染H1N1流感病毒的概率。从而我们可以认为感染甲型H1N1流感的机率与性别有一定的关系，由于感染人群中男性所占比例远高于女性，我们进一步推测男性比女性更易感染甲型H1N1流感病毒。

对四格表的抽样方式，检验方法没有明显差别。x2检验统计量由于其直观性，使得人们更容易理解和接受。虽然似然比检验统计量 - 2 ln(L)稍微复杂于x2检验统计量而不容易被人们所理解，但是似然比检验统计量 - 2 ln(L)却有着x2检验统计量所不具备的优点，那就是似然比统计量 - 2 ln(L)可以分解，这极大增加了似然比检验统计量在假设检验中的优势。关于x2检验和似然比检验的比较以及可分解性的详细叙述见参考文献[9]。正因为似然比检验统计量可分解，所以对四格表的独立性检验问题，人们除了使用直观的x2检验外，还可使用似然比检验做对照。似然比检验除了用于分类数据的检验问题，还可用于其他类型数据的检验，它的应用范围较x2检验广。

[1] 李威，宋艳玲，王长科.甲型H1N1流感在美国传播期和墨西哥暴发期的气象条件与中国初夏气候特点和相似分析 [J].科技导报， 2009，27（11）：19-21.

[2] Wei L，Yanglin S， Changke W. Comparability analysis between the climate characteristics of early summer in China and the meteorological conditions during the periods that the A(H1N1) flu spread in America and broke out in Mexico[J].Science & Technology Review， 2009， 30（11）：19-22.

[3] Shuai ZW，Qian B，Tian W， et al. Construction and expression of eukaryotic expression vector of NS1 protein of influenza A(H1N1)[J]. J Cell Mol Immunol， 2011， 20（3）： 287-289.

[4] Chan CH，Lin KL, Chan Y. Amplification of the entire genome of influenza A virus H1N1 and H3N2 subtypes by reverse-transcription polymerase chain reaction[J]. Journal of Virological Methods， 2006，35（136）： 38-43.

[5] Guo L， Garten RJ， Fonat AS， et al. Rapid identification of oseltamivir-resistant influenza A(H1N1)viruses with H274Y mutation by RT-PCR/restriction fragment length polymorphism[J]. Antiviral Research， 2009， 12（1）：29-33.

[6] 北京卫生信息网疫情周报[EB/OL]http：//www.bjhb.gov.cn/news.do?dispatch=readById&id=28342&typeid=F.2009-11.

[7] 王静龙，梁小筠.定性数据分析[M].上海：华东师范大学出版社，2005：44-45.

[8] 王静龙，梁小筠.定性数据统计分析[M].北京：中国统计出版社，2008：18-19.

[9] 王静龙，梁小筠.定性数据统计分析[M].北京：中国统计出版社，2008：232-238.

[10] 茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].第2版.北京：高等教育出版社，2012：395-396.

[11] James BC，James OA. Using SPSS： An Interactive Hands-On Approach[M]. CA： SAGE， 2012：12-200.

[12] Gilat A. Matlab： An Introduction with Applications[M].NJ： John Wiley & Sons， 2011：193-246.

[13] B. Ruth， B. Stephen， Schaum's Outline of Elements of Statistics II： Inferential Statistics[M]. NY： McGraw-Hill，1999：201-239.