贝特朗悖论之争的终结

张 敏，何小亚

（华南师范大学 数学科学学院，广东 广州 510631）

贝特朗悖论之争的终结

张 敏，何小亚

（华南师范大学 数学科学学院，广东 广州 510631）

贝特朗悖论之争主要有5种类型，争论的本质体现在4个方面．贝特朗悖论产生的原因是原问题缺少具体的等可能性假设之条件．几何概型的等可能性假设必须明确地给出，它无法通过直觉获取，也不能通过实践验证．从直观的、直觉的、现实世界的角度去看数学世界的内容是引起贝特朗悖论争论的本质原因．深刻理解这些观点对几何概率教学有重要的指导作用．

贝特朗悖论；几何概率；样本空间；等可能性假设

1 导 论

1.1 研究背景

人们对概率的研究有悠久的历史．从16世纪开始，意大利的一些学者就开始研究掷骰子等赌博中的一些简单问题．1812年，法国数学家拉普拉斯撰写了《分析概率论》这一著作，概率的古典定义在书中被首次完整而系统地提出．作为对古典定义的补充和推广，在无限样本空间背景下的几何概率也得到了广泛的应用．

正当古典概率和几何概率在各自的研究范围内迅猛发展时，1899年，法国数学家贝特朗（Joseph Bertrand, 1822—1900）提出一个“简单”的问题：在半径为R的圆内任作一弦，求其长超过圆内接正三角形边长的概率．按照几何概率的定义进行计算，竟然可以求得3个不同的概率，这与概率的性质是背道而驰的．这就是著名的“贝特朗悖论”，矛头直指几何概率概念本身．贝特朗悖论说明原来关于概率的定义带有很大的局限性，迫切需要一种公理化体系改造概率论．1933年，前苏联数学家科尔莫戈洛夫提出了概率的公理化体系，迅速获得举世的认可，使得古典概率和几何概率具有了更加严密的逻辑基础，像“贝特朗悖论”这类自相矛盾的问题也得到了合理的解释．

1.2 问题提出

公理化体系下的概率定义和古典定义以及几何定义有明显的不同．公理化定义[1]只解决“什么是概率”的问题，但并不解决“如何确定概率”的问题．贝特朗悖论的3种不同的解答，是从不同的角度分析问题，所确定的3个不同概率均满足公理化定义的3个公理化性质，因此，在公理化体系下，都被认为是正确的．关于贝特朗悖论的争论似乎可以平息了，然而，争论真的结束了吗?

随着中国高中数学新课标的实施，作为解决实际问题的一种有用工具，概率成为高中数学的必修内容[2]，并且越来越受到重视[3～6]．古典概率和几何概率是高中概率学习的重点[7]，其中几何概率更是难点．即使有公理化体系的解释，作为几何概率的一个典型问题，贝特朗悖论却一直是广大一线教师们讨论的热点问题．

比如，同一个随机事件为何会有3个不同的概率？是否违背了概率是随机事件客观属性这一性质？3种解法能否统一？3种解法是否都正确理解了原题意？是否还有另外的解法存在？

因此，关于贝特朗悖论的争论远远没有结束，教师们的疑惑仍然没有消除．这里旨在分析目前国内高中教学中关于贝特朗悖论问题的各种争论，剖析各种争论的实质，希望广大一线教师们在贝特朗问题上有正确的理解，不再困惑重重．

2 贝特朗悖论的经典解法

首先，关于几何概型和几何概率，有如下定义[1]：

若随机试验满足以下两个条件：（1）试验的样本空间中的基本结果有无穷个且不可数，充满某个区域；（2）每个基本结果是等可能出现的，即任意一点落在度量相同的子区域内是等可能的．则这样的随机试验称为几何概型．

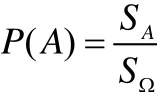
在贝特朗问题提出时，贝特朗就提出了3种经典的解法：

假设事件E表示“在半径为R圆内任作一弦，其长超过圆内接正三角形边长”．

图1

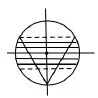
图2

图3

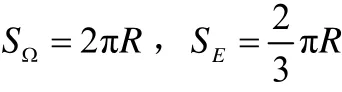
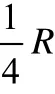
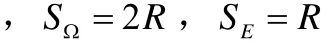
解法3：如图3，圆内弦的位置被其中点唯一确定．在圆内作一同心圆，其半径仅为大圆半径的一半，则当弦的中点落在小圆内，弦长才能超过内接正三角形的边长．

3 各种争论观点的归纳

由此看到，贝特朗问题之所以出现3种不同的答案，是因为人们观察随机试验的基本结果的角度不同，同时对基本结果的等可能性假设也有不同的理解．

然而，仍然有不少学者对此持怀疑态度，并根据自己对问题的理解以及自己特有的思维方式，钟情于其中的某种解法，想方设法寻找其他解法的瑕疵，推翻其他解法的合理性，从而认为贝特朗悖论并不奇，答案其实是唯一的．

3.1 认为解法1唯一正确

贝特朗悖论的关键在于题干中的一个条件：在圆内任作一条弦．对任意的不同理解造就了这个看似简单的问题成了“悖论”．如果认为弦是由两端点决定，任意作弦就应该先随机确定两端点在圆上的位置，这时需要假设两端点在圆上等可能分布．持这种观点的学者徐明[8]，许丽丽[9]将会认为解法1是正确的．而如果按照解法2和解法3所认为的等可能性假设，却无法推出两端点在圆上等可能分布，故认为解法2和解法3是错误的．

另一种观点认为[10]，因为解法1避开了“圆心”，故只有解法1才是正确的．在解法2中，假设任意弦的中点在与弦垂直的直径上是等可能分布的．在解法3中，假设所有弦的中点在圆中等可能分布．对于圆中的弦，除了直径外，均有唯一的弦中点与弦对应．而圆心，却是所有直径共同的中点，即这个中点特别“厚”，因此认为弦的中点在某直径或在圆内是等可能分布是不成立的．

石启亮[11]通过随机模拟的方法，按照解法1的假设，认为解法1的答案才是正确的．

3.2 认为解法2唯一正确

黄晶晶[12]认为解法2才是正确的．其主要观点基于一个假设：弦是由点组成的，长的弦需要更多的点，故任一弦出现的概率与其长度有关．由此计算得到解法2才是正确的．而解法1和解法3的情况，若按该假设重新计算，也能得到解法2的答案．

3.3 认为解法3唯一正确

张晓强[13]认为，因为其他两种解法把弦重复计算了，故只有解法3是正确的．甚至可以把其余两种解法通过剔除重复计算的弦而修改为解法3的答案．

李贵俊[14]，孙桂秋[15]，杨培恒[16]认为，在贝特朗悖论的3种解法中，有的解法对作弦有限制．比如解法1要求先固定弦的一端，解法2要求先规定弦的方向．而原题要求在圆内任意作弦，故作弦时附加的这些条件是不合理的．而解法3没有这些特殊要求，因此解法3才是符合题意的作弦方法．

3.4 认为3种解法都不对发现了其它的“唯一正确”的解法

有学者认为3种经典解法均有值得商榷的地方，故创造出有别于3种解法的新解法，并且认为更合理，甚至认为他们的解法才是唯一正确的解法。主要有以下两种：

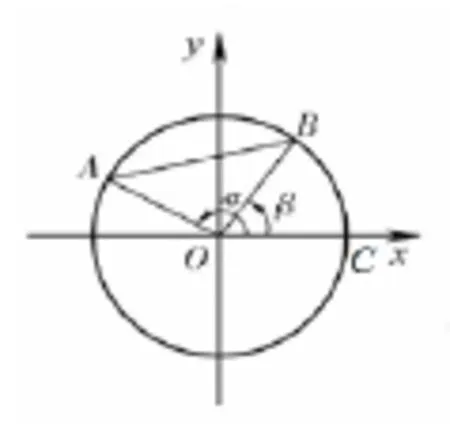
图4

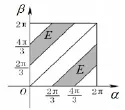
图5

这种解法的本质是：在解法一的基础上，不再预先固定弦的一端，而让弦的两个端点随机独立选取．这时的试验结果是弦的两个端点的位置，并假设两个端点各自在圆周上等可能分布．用二维点(α,β)表示试验结果，其中α表示OC按逆时针方向旋转至OA所经过的角度，β表示OC按逆时针方向旋转至OB所经过的角度，C是圆周与x正半轴的交点．0≤α≤2π，0≤β≤2π．

解法5（李文明[18]）：在半径为R的圆上随机取弦，每取一弦，记录其长度，这时试验的结果可认为是弦的长度．记弦的两端点分别为A，B，则弦AB的长度的取值范围为[0,2R]．半径为R的内接等边三角形的边长为，故只有那些弦长大于的弦才符合要求．见图6．

图6

4 剖析各种争议的实质

由此看来，贝特朗悖论至少有5种解答．这5种观点各执己见，坚持认为自己的才是正确的，因为都能找到其它解法的瑕疵．下面，从几何概型的基本要素（样本空间的构造和作弦的等可能性）对以上争议进行深入的分析．

4.1 各种解法中样本空间的构造的合理性分析

样本空间中的元素是试验的基本结果．贝特朗悖论的题意是要求在圆内任意作弦，直观看来，试验的结果应该是做出的弦．但是几何概率问题中试验的基本结果应该用“点”来描述，这个点根据实际情况可以是一维数轴上的点，也可以是二维平面上的点，或者是三维空间上的点．故求解贝特朗问题的首要任务是要把做出的弦转化成相应的“点”，即样本空间的元素．而弦和点之间应存在对应关系．上述的5种解法均从各自的角度把试验的结果转化成样本空间中的“点”．

另外，当对作弦附加了条件，比如指定弦的端点（解法1）和指定弦的方向（解法2），会否缩小样本空间？

圆内任一条弦，总是由弦在圆上的两个端点决定，而且也必然垂直于某一条直径．

解法1中，在圆周上任取一点，作为弦的一端，然后讨论弦的另一端点的位置．根据圆的对称性，以及取点的任意性，固定一端点后所作的弦的性质与固定其他点所作的相应弦的性质相同，当然包括概率这个性质．故虽然表面上看起来解法1的样本空间比解法3的样本空间要小，但所求的概率是合理的．

解法2中，预先任意确定弦的方向，考虑在这个方向上的弦的性质．由于这个方向也是任意的，在这个方向的弦的性质与其他方向上的弦的性质相同．因此虽然样本空间比解法3的样本空间小，但所求的概率也是合理的．

4.2 各种解法中作弦的等可能性分析

究竟哪种方法真正等可能地作弦？这是最困扰人们的问题．实际上，古典问题和几何问题的一个最大区别，在于可数和无限不可数的问题．其中几何问题上涉及的无限不可数问题是很抽象的问题．若根据古典的思想，用弦的数量多少或者点的数量多少来解决问题，是不正确的．

在古典概型中，由于试验基本结果是有限的，当样本空间确定后，试验基本结果的等可能性是可以验证的．但是，几何概型却并非如此．

在几何问题中，当样本空间确定后，试验结果的等可能性质却需要明确假定．而且由于试验结果的无限性，这种假定无法验证．这是人们最容易忽视和无法理解的问题．

贝特朗悖论问题恰恰是缺少了相应的等可能性假定，题干只要求在圆内任意作弦，至于弦在圆内是按何种方式等可能分布，是没有提及的，才导致如此多的“解法”．

因此，这并不算一种悖论，只是一道条件不充分的数学题，不同的人为了“解”它而添加不同的条件，将其改造成各种不同的可解的问题而已．解法1和解法4强调弦由端点决定，假设端点在圆上等可能分布；解法2强调弦由其中点决定，并假设弦中点在与弦垂直的直径上等可能分布；解法3强调弦由其中点决定，假设中点在圆内等可能分布．解法5假设弦长是等可能分布的．

这是各种不同的等可能假定，是不能够互相转化的．比如，当认为弦由端点决定，假设端点在圆上的等可能分布时，必然使得另外几种情况的等可能性假设失效．当作不同的假定后，计算的结果也就不同了．

所以，这几种方法实际上都做到了真正的等可能取弦．

4.3 关于圆心的说明

圆心，这个特殊点，在贝特朗悖论争论中担任了重要角色．在解法3中，假设弦的中点在圆内等可能分布．但是圆心这个特殊的弦中点确实比其他弦的中点“厚”，因为它是所有直径的共同中点．而圆内的其他点都只是某一条弦的中点．这时假设弦的中点在圆内等可能分布的这种等可能性假设是否合理？答案是肯定的．

古典概型和几何概型均有对试验基本结果的等可能性要求．古典概型的等可能性要求试验的每一个基本结果出现的可能性大小相同．但是几何概型的试验结果是无限不可数的，其等可能性条件的实质并不是要求每一个试验的基本结果出现的可能性大小相同．

几何概率的计算公式已表明，几何问题的概率是由试验结果所构成的测度所决定，单个试验结果的测度为0，甚至有限个试验结果的测度之和也为0，因此，几何问题中的每一基本试验结果出现的概率必相同——概率为0．这和概率为零的事件并非一定是不可能事件是相同道理的．

由此可见，考虑每一个基本试验结果的可能性大小并没有意义．几何概型中的等可能性强调的是试验结果落在度量相同的子区域内是等可能的，不管该区域的形状如何．

因此，圆心的特殊性质并不影响概率的计算，也不影响等可能性假设．一种极端的想法是甚至可以把圆心挖掉，少了这个圆心不会影响任何事件概率计算的正确性．

4.4 关于作弦的概率与弦长有关的假设

有人认为，由于圆内的所有点是等可能分布的，而不同长度的弦由于含有不同数量的点，因此作不同长度的弦是不等可能的，作长的弦比作短的弦概率大．这种说法并不合理．

弦虽然是有限长度的线段，但是不同长度的弦所包含的点均是无穷多个，这属于实无限思想的范畴．在实无限领域，可以证明不同长度的两条线段中的点存在一一对应的关系．德国数学家康托尔（Cantor, Georg Ferdinand Ludwig Philipp, 1845—1918）甚至成功证明了一条直线上的点能够和一个平面上的点一一对应，也能和空间中的点一一对应．从这种意义上说，不同长度的弦包含的点其实是一样多的，故认为作弦的概率与弦长有关的假设是不合理的．

5 结 论

5.1 贝特朗悖论并不奇

贝特朗悖论确实不奇，这并不是指它应该有唯一的答案，而是指它其实是一道开放性的，条件并不充分的题目，当把题目补充完整后，答案就唯一．这个不充分的条件正是关于弦的等可能性分布的假定．只是有的人对任意作弦的方式有个人偏好，因此倾向于某种等可能性假设，而偏向于某种解法．而实际上，这种假定甚至还不限于本文所提及的5种，所以贝特朗悖论的答案非但不唯一，甚至是有无数个解．当然，当等可能性条件补充完整后，贝特朗问题的解就唯一了．

5.2 几何概率问题中的等可能性假设是一种数学假设并无法验证

虽然几何概型和古典概型在确定概率时都要求试验结果满足某种等可能性条件，但是古典概型中的等可能性条件是可以验证的，而几何问题中的等可能性假设必须明确给出，并且无法通过直觉获取也不能通过实践验证．

几何问题涉及的是无限不可数问题，试验结果通常是用点、线、面、体等几何元素表示．“点”动成“线”，“线”动成“面”，“面”动成“体”，也就是说几何世界是由“点”构造出来的，但“点”是没有大小的东西，它在现实世界中是不存在的．数学源于现实，脱胎于现实，但它已经完全超越现实，在数学世界与现实世界之间存在着不可逾越的鸿沟．从直观的、直觉的、现实世界的角度去看数学世界的内容是引起贝特朗悖论争论的本质原因．

[1] 茆诗松，程依明，濮晓龙．概率论与数理统计[M]．北京：高等教育出版社，2011．

[2] 《国家高中数学课程标准》制订组．《高中数学课程标准》的框架设想[J]．数学教育学报，2002，11（2）：36-41．

[3] 孙名符，谢海燕．新高中数学课程标准与原教学大纲的比较研究[J]．数学教育学报，2004，13（1）：63-66．

[4] 李俊．学习概率中认知的发展[J]．数学教育学报，2002，11（5）：1-5．

[5] 蔺云．哲学与文化视角下概率统计课的育人功能[J]．数学教育学报，2002，11（2）：24-26．

[6] 蔺云．珍视概率统计课程中思辨数学的教育价值[J]．数学教育学报，2010，19（3）：18-21．

[7] 钟志华．对高中新课程中概率教学的认识[J]．数学教育学报，2006，15（1）：82-85．

[8] 徐明．“几何概型”教学释疑——兼谈“贝特朗概率悖论”[J]．数学通讯，2009，（6）：15-17．

[9] 许丽丽．由贝特朗问题谈几何概型中的等价转化[J]．教育教学：福建基础教育研究，2011，（8）：30-31．

[10] 苏同安．都是圆心惹的祸——“贝特朗悖论”新说[J]．中学数学高中版，2010，（1）：64．

[11] 石启亮．解读贝特朗_Bertrand悖论[J]．数学教学，2005，（10）：32-34．

[12] 黄晶晶，黄世同．关于贝特朗悖论的新思考[J]．昆明师范高等专科学校学报，2004，（4）：10-12．

[13] 张晓强．贝特朗“奇”论不奇[J]．牡丹江教育学院学报，2009，（4）：108．

[14] 李贵俊．贝特朗（Bertrand）悖论的探讨[J]．丹东纺专学报，2001，（4）：50-51．

[15] 孙桂秋．贝特朗奇论并不奇[J]．工科数学，1992，（2）：91-92．

[16] 杨培恒．关于贝特朗奇论的讨论[J]．陕西师大学报：自然科学版，1990，（4）：76-77．

[17] 陈作清．关于贝特朗奇论的新见解[J]．西北民族学院学报，1998，（1）：64-65．

[18] 李文明．关于贝特朗悖论的探索与进展[J]．中学数学研究，2013，（2）：47-50．

The End of Bertrand Paradox Debate

ZHANG Min, HE Xiao-ya
(School of Mathematics Science, South China Normal University, Guangdong Guangzhou 510631, China)

The debate of Bertrand Paradox mainly concludes five types and the essence of the debate lies in four aspects. The reason of Bertrand Paradox is the lack of explicit equal- possible hypothesis. Equal-possible hypothesis must be given definitely. It can neither be acquired by instinct nor be confirmed by practice. The essential reason of the debate of Bertrand Paradox is that we understand the mathematics world in visual, intuitive and real perspectives. Deep understanding about these views has great influence on geometric probability teaching.

Bertrand Paradox; geometric probability; sample space; equal-possible hypothesis

G40-055

：A

：1004-9894（2015）03-0051-04

[责任编校：张楠]

2015-01-08

教育部哲学社会科学研究重大课题攻关项目——我国高中阶段学生核心素养的模型及指标体系研究（13JZDW009）

：张敏（1977—），女，广东陆丰人，讲师，博士研究生，主要从事数学素养及概率统计教学研究．