波浪与带窄缝多箱体作用共振现象的模拟研究

宁德志，苏晓杰，滕斌

（1.大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024）

波浪与带窄缝多箱体作用共振现象的模拟研究

宁德志1，苏晓杰1，滕斌1

（1.大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024）

针对波浪与带有窄缝多箱体结构作用产生的流体共振问题，建立了基于域内源造波技术的二维非线性时域数值波浪水槽模型，其中自由水面满足完全非线性运动学和动力学边界条件，窄缝内流体引入人工阻尼来等效由于涡旋运动和流动分离引起的黏性耗散，计算域边界采用高阶边界元进行离散。通过模拟三箱体间两窄缝内相对波高变化，并与已发表的数值与实验结果对比，验证了本模型的准确性。同时通过大量的数值计算，分析了箱体数量对窄缝内水体共振频率、共振波高以及对结构反射波高和透射波高的影响。

窄缝；流体共振；域内源造波技术；高阶边界元；非线性数值波浪水槽

1 引言

为了充分利用海洋空间资源，由多模块组成的超大型浮体已在海洋工程领域得到利用［1］，譬如用作海上机场、军事基地、储存器和海难救助点等，国内外学者已经开展了很多有关超大型浮体水动力特性的研究，如波浪冲击［2］，水弹性运动响应［3］，非稳定外荷载作用下的动力响应［4］等。由于组成超大型浮体的各个模块之间并不是无缝连接，大都存在相对模块特征长度很小的窄缝，缝隙内的水体在某些频率波浪作用下会发生共振现象，诱发很大的波浪爬高和荷载，进而对海洋结构的作业安全带来很大的影响。

有关海洋结构物间窄缝内波浪水动力特性问题，国内外已经开展了许多相关理论、模型试验和数值模拟研究，但大多数研究目前还只是局限于两个结构或3个结构间缝隙水体共振问题。譬如，Miao等［5］采用渐近匹配法研究了带狭缝二维双箱的共振现象，给出了狭缝很小时双箱的理论共振频率。Saitoh等［6］对不同入射波浪作用下两个方箱间窄缝的波高变化进行了试验研究，发现窄缝内最大共振波高可以达到入射波高的5倍。Kristiansen和Faltinsen［7—8］对波浪与具有窄缝的二维固定及浮式箱体和固定式岸壁结构之间的相互作用分别开展了数值和试验模拟，发现线性和非线性势流数值结果都比共振条件下的窄缝内试验波高要大，尤其是线性结果更大；并研究了共振条件下浮体3个自由度的运动响应与水动力系数。在三体结构双缝隙方面，Iwata等［9］分别对不同入射波浪作用下3个方箱之间窄缝的波高变化进行了试验研究，发现共振频率与箱体的吃水深度、窄缝宽度和箱体个数成一定的函数关系。何广华等［10］采用比例边界有限元方法分别研究了波浪与三箱结构作用下窄缝内水体共振现象。Lu等［11—12］采用黏性流模型和改进的线性势流模型对三体结构间窄缝内水体共振引起的波浪爬高和波浪荷载进行了研究，并发现在窄缝内自由水面上布置一定的人工阻尼时，势流模型也可以得到与试验和黏性流模型相一致的结果。通过上述研究发现，三箱体间窄缝内水体共振频率明显不同于双箱浮体情况，甚至出现多个自振频率等复杂情况，也进一步说明箱体数量对窄缝内水体运动特性具有重要影响，而目前对于3个及以上浮体间窄缝内水体共振问题的研究还很少。

本文将在前人研究基础上，建立自由水面满足完全非线性边界条件的二维时域数值波浪水槽模型，采用域内源造波方法产生入射波浪并布置前置阻尼层消除二次反射影响，实现在较小计算域内进行长时间模拟；参照Lu等［11］的方法在窄缝水体自由水面上引入常人工阻尼系数来等效共振条件下黏性耗散。通过模拟波浪与3箱体间双窄缝内水体运动问题，并与Iwata等［9］实验结果及Lu等［12］的CFD数值结果进行对比，证明了本模型的准确性。进而通过大量数值计算研究了箱体数量（最多至6个）对窄缝内水体共振频率、共振波高以及对结构迎浪侧反射波高和背浪侧透射波高的影响，总结一般性规律，为如超大型浮体这样由多模块组成的具有窄缝的海洋结构水动力分析提供参考。

2 数学模型

考虑单向规则波浪与具有窄缝的多固定箱体相互作用问题，其布置如图1所示。建立二维笛卡尔坐标系Oxz，z＝0位于静水面上，且z轴向上为正，x轴右方向为正。计算域包含自由水面Гf和固体边界ГN（包括水底Гd和箱体Гb）。波浪由控制垂直源造波面（Гs）的流量密度产生。图中h为水槽静水深，W为箱体宽度，D为箱体吃水深度，Wg为两箱体间窄缝的宽度，N为箱体个数，本研究中取值为2、3、4、5、6。考虑问题一般性，本文中假定各个箱体的宽度、吃水深度和缝隙宽度均一致，图1中迎浪侧e点、背浪侧f点和各个箱体件窄缝（gap）内波高变化规律是本文研究的重点。在流体无黏、不可压缩和流动无旋的假定下，整个流域的速度可用速度势的梯度来描述，上述问题的控制方程为由速度势满足的泊松（Poisson）方程［13］，即

式中，q*（xs，z，t）＝2Vδ（x－xs）为造波源强度；造波位置x＝xs（本文均取xs＝0）；V为流体质点水平速度，本文给定二阶Stokes速度解析解。

在自由水面上，满足完全非线性动力学和运动学边界条件，本文中采用混合欧拉-拉格朗日方法更新自由水面，利用物质导数，并在计算域的上游和下游区域的自由水面分别布置人工阻尼层来吸收从结构物反射回来的波浪与出流波浪［14］，在窄缝内布置一常参数人工阻尼来近似由于涡和分流引起的黏性耗散［15］。自由水面边界条件可以写成以下形式：

式中，η代表自由水面的铅垂位移，g是重力加速度，X0＝（x0，0）是指水质点初始静止时的位置，阻尼系数

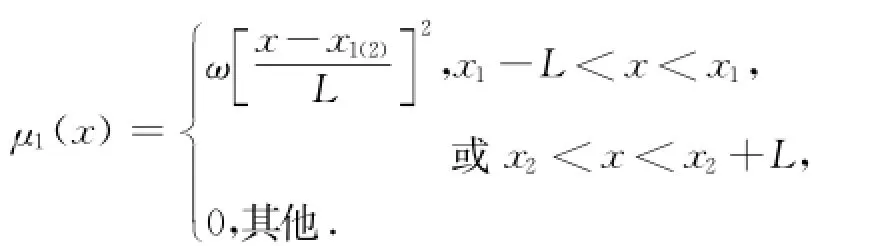
用于计算域边界的两个阻尼层，x1和x2分别是左右两侧阻尼层的起点位置；L为阻尼层长度，本文取1.5倍波长（即1.5λ）；ω是波浪角频率。阻尼系数μ2用于窄缝内自由水面，其数值根据试验黏性耗散来确定；k是波数，满足如下线性色散方程关系

在固定的结构表面和底面边界上，流体法向速度为0，满足固壁不可渗透边界条件。由于本研究在时域内进行，自由水面满足静初始条件，即起始时刻速度势和波面均为0。

对于满足上述控制方程和边界条件的定解问题，在整个流域内对速度势应用格林第二定理，可转换如下边界积分方程［13］：

式中，p＝（x0，z0）为源点；q＝（x，z）为场点；C为固角系数；Ω代表整个流域；G是简单格林函数，考虑到水底镜像，可以表示为如下形式：

式中，r1为p和q两点距离，

r2为p和q关于水底镜像之间距离，

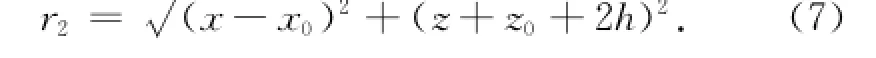
本文用三节点高阶边界元离散计算域成一些曲线单元，单元内任一点的几何坐标和速度势等物理量可以用如下二次形状函数hi（ξ）插值得到，

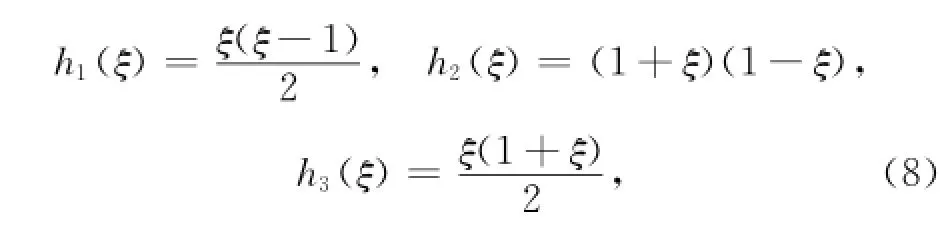
式中，ξ代表固有坐标，取值范围（－1.0，1.0）。

这样在任一边界单元内，物理量和几何量都可以通过形状函数插值得到，也即，边界单元都是等参的。积分方程（4）经高阶边界元离散后，可以表示成如下形式：

式中，Ne1、Ne2、Ne3分别为自由水面、物面和出入流边界及造波源面上划分的单元个数，J（ξ）是联系大地坐标和固有坐标的雅可比行列式。

由于本文采用了高阶边界元方法，自由水面边界条件式（2）中用到的速度势的空间导数项进而可以表示成如下形式：

式中，n＝（nx，nz）为单位法向量，指出水体为正。

最后把未知量都移到方程（9）的左侧，该方程组就可以写出如下矩阵乘积形式：

式中，X是未知的速度势和速度势法向导数，A为空间系数矩阵，F为由已知的速度势和速度在边界上积分得到的列向量。

计算中认为当前时刻物面上的速度势法向导数和自由水面上的速度势是已知的，根据积分方程计算当前时刻物面上的速度势和自由水面上的速度势法向导数，然后应用四阶Runga-Kutta法，根据自由水面条件式（2）计算下一时刻的水质点位置和自由水面上的速度势，再用二次形状函数在旧单元上插值求得新节点上的物理量来对自由水面网格重新划分，重新应用积分方程计算下一时刻物面上的速度势和自由水面上的速度势法向导数。这样计算周而复始，直到计算结束［16—17］。

3 数值计算及讨论

3.1 模型准确性和稳定性

作为算例，本文以Iwata等［9］的实验来进行数值模拟波浪与具有窄缝的三箱体的相互作用的研究，验证本文数学模型的准确性。这里选用的实验参数为水槽静水深h＝0.5 m，箱体的宽度W＝0.5 m，吃水深度D＝0.252 m，入射波高H0＝0.024 m，箱体间窄缝宽度0.05 m。在数值模型中，计算域长度取7.5倍波长，在水槽的左右两端各布置1.5倍波长的阻尼层，造波源位于x＝0，箱体1左侧面边界位于距离造波源2.5倍波长的位置，然后依次按Wg调整箱体2和3的位置。通过开展数值收敛性实验，自由水面上每个波长布置15个单元，窄缝内布置2个单元，计算域垂向边界和造波源面分别布置10个单元，箱体侧面边界上均布置6个单元，底面边界上均布置12个单元；时间步长Δt＝T／60 s，每个算例模拟30个周期。

图2给出了窄缝宽度Wg为0.05 m情况下两个窄缝中心位置无量纲波高Hg／H0随入射波波数kh的变化关系，及本文数值结果与实验数据［9］、黏性流模型数值结果［12］的比较。由于窄缝内水体黏性与波浪条件无关，故在某一波浪频率下通过取一系列不同人工黏性系数进行数值模拟，并与实验数据进行对比，确定窄缝中间水面的人工黏性系数取为μ2＝0.03；数值模拟中，波高Hg以测试点的稳定时间段内波面时间序列中波峰值与波谷绝对值和的平均来计算。从图中可以看出，箱体1与箱体2之间窄缝内数值模拟波面高在kh＝1.35时达到最大，也即窄缝内流体发生共振，波高为入射波高的4.6倍。箱体2与箱体3之间窄缝内数值模拟波面高在kh＝1.4时达到最大，波高为入射波高的4.4倍。同时发现窄缝1内出现2个共振频率，这与单缝隙内的共振规律是不同的，也进一步说明浮体数量对窄缝内水体运动规律的重要影响。整体上两种数值结果与实验数据均符合的很好，在个别位置处甚至本文结果比黏性流模型结果与实验数据吻合的更好，说明所建立模型在取得合适的人工黏性系数情况下可以准确模拟多箱体窄缝内流体共振问题。

图3给出了波数kh＝1.40，窄缝宽度Wg＝0.05 m，入射波高H0＝0.024 m情况下t＝26T和30T时的整个计算域波面分布，图中虚线分界处分别对应3个箱体所在的位置。从图中可以看出，两个时刻的波面曲线已经完全重合，包括箱体1前的反射波，箱体3后的透射波和3个箱体之间的窄缝内波面；并且两端的波面基本趋于0，说明两端阻尼层吸收波浪的效果很理想；箱体1前的波浪形成了稳定的立波，说明其反射回去的波浪透过造波源被前端阻尼层完全吸收，而对入射波浪没有产生影响。以上现象说明本模型的模拟结果已达到稳定。

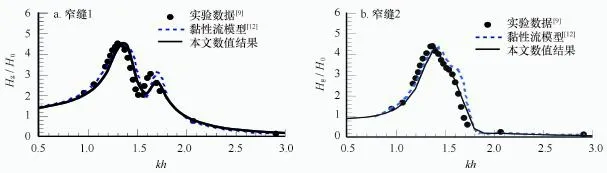
图2 两窄缝中无因次波高Hg／H0与波数kh间的关系Fig.2 Distribution of non-dimensional wave height versus incident wave number at two narrow gaps

图3t＝26T和30T两个时刻的水槽波面分布Fig.3 Snapshot of wave elevation along the wave flume att＝26Tand 30T

3.2 数值结果

下面仍以上述工况为例，保持各参数不变，只是改变箱体数量，进一步分析箱体数量对窄缝内水体共振频率、波浪爬高以及结构前反射波高和结构后透射波高的影响。

图4和图5是箱体个数N分别为4和5时各个窄缝内无因次波高Hg／H0随入射波波数kh的变化关系。各窄缝的主共振频率相仿，其所对应的共振波高在处于中间位置的窄缝内达到最大。在大于主共振频率的某一频率处，还会有次共振现象发生，且处于两端位置的窄缝内较中间位置的窄缝内次共振现象更为明显，尤为突出的是迎浪侧的窄缝内，在图5的窄缝1中高共振频率所对应的共振波高已大于其低共振频率所对应的波高。其原因可能是各窄缝内自振频率下的波浪会向两侧传播并与迎浪侧透射的波浪相互作用，处于中间位置的窄缝由于对称关系，从窄缝两侧反射来的波浪叠加达到最大，而处于边界的窄缝由于其相对位置关系则会发生复杂的波浪干涉现象。

图4 4箱体时各窄缝内波高随波数的变化关系Fig.4 Dimensionless wave height againstkhat various gaps for four boxes

图6和图7分别为不同数量箱体时窄缝1（即迎浪侧第一个窄缝）和窄缝N－1（背浪侧第一个窄缝）内无因次波高随波数的分布情况。可以看出随着箱体数量的增加，主频共振发生时，窄缝内波高减小，对应的共振频率向低频偏移。并且箱体数量较多时，窄缝会在多个频率发生共振，且高共振频率处的波高随箱体个数的增加而增大，窄缝1内在箱体数N为5和6时已大于低共振频率处的波高，窄缝5内高频共振波高也大于低频共振波高。各个工况下窄缝N－1内主共振频率都不小于窄缝1内主共振频率，而窄缝1和N－1内相邻箱体数对应的次频共振频率的差值近似常数（Δkh≈0.1）。

图5 5箱体时各窄缝内波高随波数的变化关系Fig.5 Dimensionless wave height againstkhat various gaps for five boxes

图6 窄缝1内无因次波高随波数的变化关系Fig.6 Dimensionless wave height againstkhat gap 1

图7 窄缝N内无因次波高随波数的变化关系Fig.7 Dimensionless wave height againstkhat gapN

表1和表2列出了不同箱体数情况下各个窄缝内对应共振频率和共振波高分布情况。可以看出，除了得到与图4、图5、图6和图7相同的规律外，还会发现对于同一箱体个数N，各窄缝内的低共振频率会从迎浪侧向背浪侧逐渐增大，对应的共振波高则是中间窄缝内最大，向迎浪侧和背浪侧两侧减小；而高共振频率则是处于中间位置窄缝内最大，向迎浪侧和背浪侧两侧减小，对应的共振波高则是中间位置窄缝内最小，向两侧增大。

表1 各窄缝对应的低共振波数和共振波高（kh，Hg／H0）Tab.1 Low resonant wave number and wave height at various gaps（kh，Hg／H0）

表2 各窄缝对应的高共振波数和共振波高（kh，Hg／H0）Tab.2 High resonant wave number and wave height at various gaps（kh，Hg／H0）

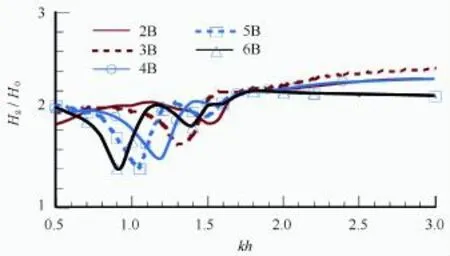
图8 迎浪侧e点波高随波数的变化关系Fig.8 Wave height at the weather-side pointeagainstkh

图8和图9分别给出了迎浪侧e点和背浪侧f点无因次波高随波数的变化关系。从图8中可以看出，在窄缝1内主频共振频率处，迎浪侧e点波高出现最小值，且箱体数N越大，对应的极值越小（N＝6时，最小的Hg／H0＝1.4），在低频处无因次波高接近于2，相当于波浪线性化并被全反射，而在高频处无因次波高会大于2，这是由于波浪的非线性增强，高阶谐波贡献所致。从图9可以看出，在窄缝N内主频共振频率处，背浪侧f点波高也出现明显的峰值，但其变化规律与图8相反，随着箱体数N的增大，透射波高的峰值也增大（N＝6时，最大的Hg／H0＝0.78），在高频处，透射波高接近于0。

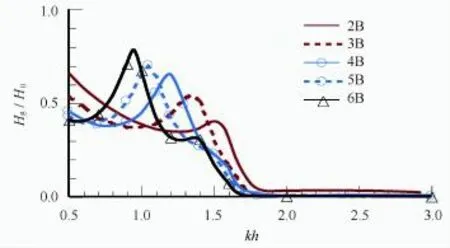
图9 背浪侧f点波高随波数的变化关系Fig.9 Wave height at the lee-side pointfagainstkh

4 结论

本文基于域内源造波的时域高阶边界元方法建立波浪与具有窄缝的多箱体结构相作用的完全非线性数值水槽模型，对不同个数箱体时窄缝内流体的共振频率、共振波高及结构迎浪侧波高和背浪侧透射波高等进行了模拟研究。通过与已发表实验数据和数值结果进行对比验证，表明本文所建立数学模型可以准确模拟波浪与具有窄缝的多箱体相互作用过程，且在较小计算域内可长时间模拟得到稳定的结果，没有在入射边界发生二次反射现象。研究发现：箱体宽度、吃水、窄缝宽度一定时，不同数量箱体，窄缝内水体发生共振的频率是不同的且箱体个数较多时会有多个共振频率。随着箱体数量的增加，主频共振发生时，窄缝内波高减小，主频共振频率值减小；次频共振频率处的波高随箱体个数的增加而增大。对于一给定箱体数N的情况，各窄缝内的主频共振频率会从迎浪侧向背浪侧逐渐增大，对应的共振波高则是中间窄缝内最大，向迎浪侧和背浪侧两侧减小；而次共振频率则从处于中间位置窄缝内最大，向迎浪侧和背浪侧两侧减小，对应的共振波高则是中间位置窄缝内最小，向两侧增大。迎浪侧波高在窄缝1内共振发生时最小，背浪侧波高则在窄缝N－1内共振发生时出现峰值；随着箱体个数的增加，共振发生时迎浪侧波高减小，背浪侧波高增大。

［1］ 缪国平，刘应中.征服海洋之梦——超大型海洋浮式结构物［J］.自然杂志，1996，18（1）：26－30.

Miao Guoping，Liu Yingzhong.A dream to conquer the ocean——super large floating ocean structures［J］.Ziran Zazhi，1996，18（1）：26－30.

［2］ Yashimoto H，Ohmatsu S，Hoshino K，et al.Slamming load on a very large floating body with a shallow drift［J］.Journal of Marine Science and Technology，1997，2：163－172.

［3］ Kagemoto H，Fujino M，Murai M.Theoretical and experimental predictions of the hydro-elastic response of a very large floating structure in waves［J］.Applied Ocean Research，1998，20：135－144.

［4］ Qiu L，Liu H.Three-dimensional time-domain analysis of very large floating structures subjected to unsteady external loading［J］.Journal of Offshore Mechanics and Arctic Engineering，2006，129（1）：21－28.

［5］ Miao G P，Ishida H，Saitoh T.Influence of gaps between multiple floating bodies onwaveforces［J］.China Ocean Engineering，2000，14（4）：407－422.

［6］ Saitoh T，Miao G P，Ishida H.Theoretical analysis on appearancecondition of fluid resonance in a narrow gap between two modulesof very large floating structure［C］／／Proceedings of the Third Asia－Pacific Workshop on Marine Hydrodynamics，Shanghai，China，2006：170－175.

［7］ Kristiansen T，Faltinsen O M.Studies on resonant water motion between a ship and a fixed terminal in shallow water［J］.Journal of Offshore Mechanics and Arctic Engineering，2009，131：021102.

［8］ Kristiansen T，Faltinsen O M.A two-dimensional numerical andexperimental study of resonant coupled ship and piston-modemotion［J］.Applied O-cean Research，2010，32：158－176.

［9］ Iwata H，Saitoh T，Miao G P.Fluid resonance in narrow gaps ofvery large floating structure composed of rectangular modules［C］／／Proceedings of the Fourth International Conference on Asian and Pacific Coasts，Nanjing，China，2007：815－826.

［10］ 何广华，滕斌，李博宁，等.应用比例边界有限元法研究波浪与带狭缝三箱作用的共振现象［J］.水动力学研究与进展，2006，21（3）：418－424.

He Guanghua，Teng Bin，Li Boning，et al.Research on the hydrodynamic influence from the gaps between threeidentical boxes by a scaled boundary finite element method［J］.Journal of Hydrodynamics，2006，21（3）：418－424.

［11］ Lu L，Cheng L，Teng B，et al.Numerical investigation of fluid resonance in two narrow gaps of three identical rectangular structures［J］.Applied Ocean Research，2010，32（2）：177－190.

［12］ Lu L，Teng B，Cheng L，et al.Modelling of multi-bodies in close proximity under water waves——fluid resonance in narrow gaps［J］.Science China Physics，Mechanics＆Astronomy，2011，54（1）：16－25.

［13］ Ning D Z，Teng B，Eatoack Taylor R，et al.Numerical simulation of non-linear regular and focused waves in an infinite water-depth［J］.Ocean Engineering，2008，35（8／9）：887－899.

［14］ Tanizawa K.Long time fully nonlinear simulation of floating body motions with artificial damping zone［J］.The Society of Naval Architects of Japan，1996，180：311－319.

［15］ Kim Y W.Artificial damping in water wave problems：Ⅰ.Constant damping［J］.International Journal of Offshore and Polar Engineering，2003，13（2）：88－93.

［16］ 周斌珍，宁德志，滕斌.造波板运动造波实时模拟［J］.水动力学研究与进展，2009，24（4）：1－12.

Zhou Binzhen，Ning Dezhi，Teng Bin.Real-time simulation of waves generated by a wave maker［J］.Journal of Hydrodynamics，2009，24（4）：1－12.

［17］ 陈丽芬，宁德志，滕斌，等.潜堤上波流传播的完全非线性数值模拟［J］.力学学报，2011，43（5）：834－843.

Chen Lifen，Ning Dezhi，Teng Bin，et al.Full nonlinear numerical simulation for wave-current propagation over a submerged bar［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43（5）：834－843.

Numerical study of fluid resonance induced by wave action on multi-boxes with narrow gaps

Ning Dezhi1，Su Xiaojie1，Teng Bin1

（1.State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，China）

Based on wave generation technique by a inner-domain source，a two-dimensional nonlinear numerical wave flume over time is developed to investigate the fluid resonance induced by the interaction between wave and multi-objects with narrow gaps.In the numerical model，the fully nonlinear kinematic and dynamic boundary conditions are set for the instantaneous free surface；the artificial damping is introduced into the gap to simulate the viscous dissipation due to vortex motion and flow separation；the computational domain is discretized using higher-order boundary elements.The proposed model is validated by the published experimental and numerical data of the relative wave height at two narrow gaps of three boxes.Numerical experiments are performed to study the following：the effects of the number of the boxes on the resonant frequency，wave height at various gaps and the reflected and transmitted wave heights of the objects.

narrow gap；fluid resonance；inner-domain source generation technique；higher-order boundary element；nonlinear numerical wave flume

O353.2

A

0253-4193（2015）03-0126-08

宁德志，苏晓杰，滕斌.波浪与带窄缝多箱体作用共振现象的模拟研究［J］.海洋学报，2015，37（3）：126—133，

10.3969／j.issn.0253-4193.2015.03.013

Ning Dezhi，Su Xiaojie，Teng Bin.Numerical study of fluid resonance induced by wave action on multi-boxes with narrow gaps［J］.Haiyang Xuebao，2015，37（3）：126—133，doi：10.3969／j.issn.0253-4193.2015.03.013

2014-01-22；

2014-04-21。

国家自然科学基金项目（51179028，51222902，51221961）；教育部新世纪优秀人才支持计划（NCET－13－0076）；中央高校基本科研业务费专项资金（DUT13YQ104）。

宁德志（1975—），男，黑龙江省五常市人，教授，博士生导师，主要从事非线性波浪及其与结构物相互作用的研究。E-mail：dzning＠dlut.edu.cn