一 脉 相 承 话 高 考——解析几何试题背景探究

●孙 明 (商城县第二高级中学 河南商城 465350)

一 脉 相 承 话 高 考
——解析几何试题背景探究

●孙 明 (商城县第二高级中学 河南商城 465350)

解析几何常借助代数方法来解决，但在解题过程中，我们不仅要关注代数运算，还应尽可能地挖掘问题背后隐藏的几何本质，将“数”和“形”统一起来，这样才能真正地提高我们对数学问题的认识水平，体会题意，探究题目的背景并进行推广，从而得出更一般的结论.

1 陈题再现——2道高考题

例1 如图1，已知抛物线C:y2=4x的焦点为F，过点K(－1，0)的直线l与C相交于点A，B，点A关于x轴的对称点为D.

1)证明:点F在直线BD上;

(2010年全国数学高考理科试题第21题) 1)证明 设 A(x1，y1)，B(x2，y2)，D(x1，－y1)，则直线l的方程为

x=my－1(其中m≠0)，将x=my－1代入y2=4x并整理得y2－4my+4=0，

则y1+y2=4m， y1y2=4.

2)略.

本题中点K与点F关于原点对称，若将它们以及抛物线一般化，可得如下结论:

结论1 已知抛物线C:y2=2px(其中p＞0)，过x轴负半轴上任一点K(－t，0)(其中t＞0)作直线交抛物线C于点A，B，点A关于x轴的对称点为D，则BD过定点F(t，0)(或点(t，0)在直线 BD上).

若联结KD，则x轴是∠BKD的平分线.

图1

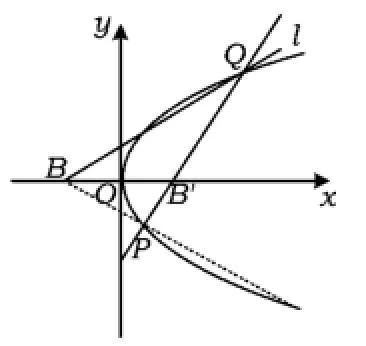
图2

例2 已知动圆过定点A(4，0)，且在y轴上截得的弦MN的长为8.

1)求动圆圆心的轨迹C的方程;

2)如图2，已知点B(－1，0)，设不垂直于x轴的直线l与轨迹C交于2个不同的点P，Q，若x轴是∠PBQ的角平分线，证明:直线l过定点.

(2013年陕西省数学高考理科试题第20题)

分析 由第1)小题求得轨迹C的方程为y2= 8x.

2)当直线l与抛物线C交于不同的2个点P，Q，满足x轴是∠PBQ的角平分线时，点Q关于x轴的对称点在直线BP上，因此，PQ一定经过点B关于原点的对称点B'(1，0).

实际上，以上2道题中的点K与点F，点B与点B'都是关于抛物线C的“反演点”.

反演点的定义 已知圆O的半径为r，从圆心O出发作一射线，若射线上的2个点M，N满足OM·ON=r2，则称M，N是关于圆O的“反演点”(注:把平面上的点M变换为关于圆O的反演点N的变换叫做“反演变换”).

图3

命题1 如图3，设M，P是圆O:x2+y2=r2上任意2个点，点M关于x轴的对称点为N，若直线MP，NP分别交x轴于M1，N1，则OM1· ON1=r2.

证明 联结M1N与圆O交于Q，则P，Q关于x轴对称，联结NO，PO，OQ，则

1从而点P，O，N，M1共圆，于是

∠OPN1=∠OPN=∠ONP=∠OM1P，得△OPN1∽△OM1P，从而

类比到椭圆有:

考虑伸压变换，即可转化为命题1，这里不再证明.

圆与椭圆、双曲线、抛物线“同宗同源”都具有类似性质，以上结论中的点 N1，M1就是关于圆x2+y2=r2的一对反演点，也可以看作是关于椭圆1的一对反演点.

2 一脉相承——1道调研题

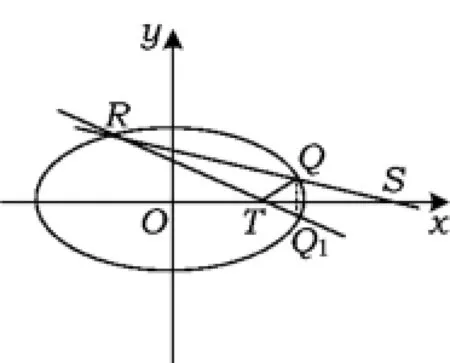
图4

例3 如图4，已知椭圆C的焦点在x轴上，左、右焦点分别为F1，F2，离心率e=，P为椭圆上任意一点，△PF1F2的周长为6.

1)求椭圆 C的标准方程.

2)过点S(4，0)且斜率不为0的直线l与椭圆C的交于点Q，R，点Q关于x轴的对称点为Q1，过点Q1与R的直线交x轴于T，试问:△TRQ的面积是否存在最大值?若存在，求出这个最大值;若不存在，请说明理由.

(2015年河南省六市高三第一次联考理科试题第20题)

(3m2+4)y2+24my+36=0，则Δ=(24m)2－4×36(3m2+4)=144(m2－4)＞0，即m2＞4.设Q(x1，y1)，R(x2，y2)，Q1(x1，－y1)，由韦达定理得

直线RQ1的方程为

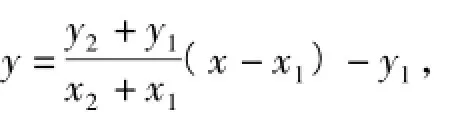
令y=0，得

将式(1)，式(2)代入上式得x=1.又

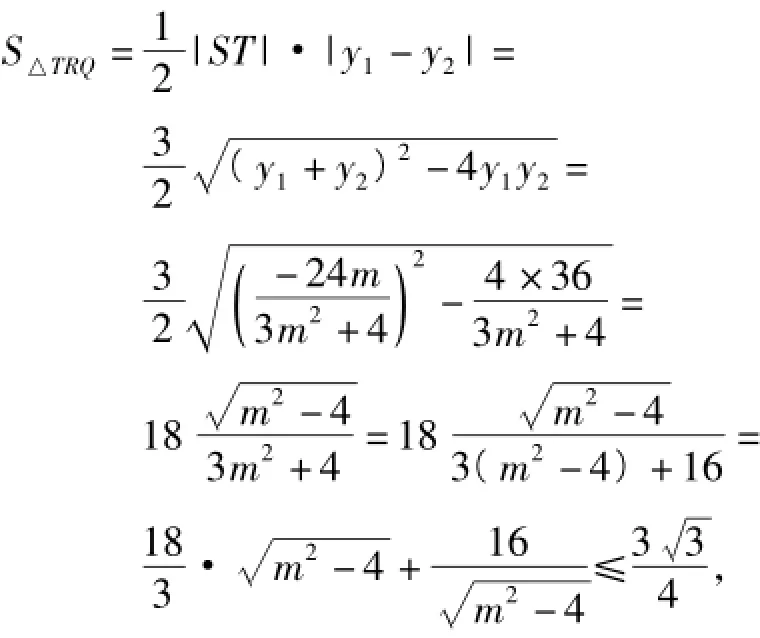
由以上解题过程可知，点T是椭圆C的右焦点，而点S是椭圆C的准线与x轴的交点.类比前面的结论，可得:

于是 y2x1+x2y1－t(y1+y2)=因此kRT=kTQ1，也即点T在直线RQ1上.

3 2015年2道高考题

图5

1)当k=0时，分别求 C在点M和N处的切线方程.

2)y轴上是否存在点 P，使得当k变动时，总有∠OPM=∠OPN?说明理由.

(2015年全国数学高考理科新课标卷第20题)

分析 1)C在点M和N处的切线方程分别是

2)假设存在符合题意的点 P(0，b)，M(x1，y1)，N(x2，y2)，直线PM，PN的斜率分别为k1，k2，将y=kx+a代入C的方程得

评注 直线l:y=kx+a(其中a＞0)过定点(0，a)，与满足条件的点P(0，－a)是关于抛物线C的反演点.

1)求椭圆C的方程，并求点M的坐标(用m，n表示).

2)设O为原点，点B与点A关于x轴对称，直线PB交x轴于点N，问:y轴上是否存在点Q，使得∠OQM=∠ONQ?若存在，求点Q的坐标;若不存在，说明理由.

(2015年北京市数学高考理科试题第19题)

图6

2)因为点B与点A关于x轴对称，所以B(m，－n).设N(xN，0)，则设存在符合题意的点 Q(0，yQ)，使得 ∠OPM=∠ONQ，则Rt△OQM∽Rt△ONQ，从而，即满足.又因为n2=1，所以于是或

评注 由|OQ|2=|ON|·|OM|，即|OR|2= |ON|·|OM|，可知点M与N就是关于圆x2+y2= 2的一对反演点，也可以看作是关于椭圆1的一对反演点.

反演点既是高中解析几何知识的潜在内容，也是高考解析几何命题的“生长源头”.数学新课标注重学生探究知识的过程，从代数形式探究几何内容无疑是认识数学、学习数学的最好方法.