基于多变点理论对全国居民消费价格指数的波动分析

刘伟棠

摘 要：居民消费价格指数在一定程度上反映了通货膨胀或紧缩的程度，因此受到社会的广大关注。本文运用多变点统计分析理论对全国（2000-2013）月度居民消费价格指数进行实证分析，通过BIC准则检验变点发生个数，在最小二乘准则下，根据动态规划原理得到最优分段及变点估计。最后，探讨全国居民消费价格指数变点发生的影响因素及波动特征。

关键词：多变点;居民消费价格指数;BIC;动态规划

一、引言

居民消费价格指数（Consumer Price Index，简称CPI），作为一种常用的总体价格水平指标，它是度量一组具有代表性消费商品及服务项目的价格水平随时间而变动的相对数，反映了居民家庭一般所购买的消费商品和服务价格水平变动情况。

价格的频繁波动，不仅会给广大市民的生活带来困扰，更不利于国家经济的健康发展。物价或许是广大市民最为关心的问题之一，对CPI的波动分析，掌握其波动特征及规律对于我国调整经济政策具有重要作用，因此，受到广大学者的研究，如方燕等（2009）[1]利用ARCH模型;杨坚等（2012）[2]利用ARMA模型;陈家清等（2013）[3]利用ACGARCH模型都对我国居民消费价格指数的波动特征及走势进行了实证分析。本文以全国（2000-2013）月度居民消费价格指数为研究对象，基于多变点理论对其进行波动分析，通过变点理论分析，认识我国2000年以来CPI的波动特征及其周期。

变点问题一直是统计学前言研究的热点问题，变点往往是模型中某个或某些量起突然变化的点，这种变化一般会反映事物的某种质的变化。本文根据Bai和Perron（1998，2003）[4][5]分析多变点理论，对我国（2000-2013）月度居民消费价格指数进行多变点分析。

二、模型及主要方法

假设一组时间序列{yt}满足下式

yt=xx′B1I（t≤t1）+xt′β2+etI（t1tk+1）+et

（1）

其中，假设k为变点个数，xt∈Rd，βi∈Rd，i=1，…，k+1，et为时刻t时随机干扰项，k个变点将序列{yt}分成k+1个分段，若βi≠βi+1，称ti为变点，且ti满足ti+1-ti≥m，其中，m表示每段至少的观察值个数。因此，检验模型（1）是否存在变点等价于检验下列假设检验：

H0：β1=β2=…=βk+1 vs H1：至少存在一个i使得：βi≠βi+1

令所需变点估计集为k，n=（t1，…，tk）。对φk，n于的估计，在给定k的情况下，根据陈希孺（1991）[6]、王锦功（1996）[7]等所构造的最小二乘法以及Bai和Perron（1998，2003）[4][5]所用的动态规划原理，可得到变点集及参数βi的估计。因此，对于第i分段，可得到关于βi的估计方程为：f（βi）=∑t=ti-1+1ti（yt-xt′βi）2，使其达到最小可得βi的最小二乘估计β∧i，且第i分段的目标函数为

r（ti-1+1，ti）=∑tit=ti-1+1（yt-xt′β∧i）2

（2）

因此，可得到全局目标函数为：R（t1，…，tk）=∑k+1i=1r（ti-1+1，ti），则变点的估计φ∧k，n（t∧1，t∧2，…，t∧k）应满足于使全局目标函数达到最小值，即

φ∧k，n（t∧1，t∧2，…，t∧k）=arg min（t1，…，tk）（R（t1，…，tk））

（3）

若k已知，根据Bai和Perron（1998，2003）[4][5]思想，通过动态规划原理得到全局目标函数最小值、最优分段以及变点估计值φ∧kn。令R（φ∧T，T）表示前T个观察值已包含r变点的最优分段，由（2）式，可得到其迭代方程为r（i，j）=r（i，j-1）+v（i，j）2，其中v（i，j）2表示序列从时刻i开始在时刻j处的观察值与理论值之差，即在时刻j处的目标函数。继而可得到动态规划迭代方程为：

R（φ∧k，n）=minkm≤j≤n-m{R（φ∧k-1，j）+r（j+1，n）}

（4）

首先，在[tm，tn-（km）]检验第一个变点，得到包含一个变点的最优分段，此分段结束时刻应落在[t2m，tn-（k-1）m]之间;在已经第一个变点时刻下，同理得到包含两个变点的最有分段，此分段结束时刻应落在[t3m，tn-（k-2）m]之间，以此类推，可得到包含k个变点的最优k+1个分段。在实际中解决变点问题时，往往变点个数是未知且一般根据数据结构估计变点个数，Yao（1998）[8]使用BIC准则估计变点个数，陈希孺（1991）[6]结合目标函数，根据其变化趋势得到变点个数估计。

三、实证分析

（一）模型及数据分析

本节将前文方法运用于全国CPI数据（上年同月=100）分析中，通过寻找突变点，对CPI的波动情况及波动特征进行分析，以我国（2000-2013）年月度CPI数据为分析对象，令yt表示时刻全国CPI实值，则CPI走势如图1所示。

图1 全国居民消费价格指数走势图

从图1中可知2000-2013年全国居民消费价格指数存在明显波动。我们构造一阶自回归模型AR（1）分析其结构，为：yt=βyt-1+et，t=1，2，…，n，其中yt表示t时刻观测值，β表示t时刻回归系数，et为均值为0、独立的白噪声序列。对于AR（1）模型，假定变点个数为k，则存在k+1个分段，每段中的系数βi为不同常数，通过单位根检验得到P值为0.4982，说明AR（1）模型是非平稳过程。

为了检验CPI结构变化，首先，通过Yao（1998）[8]所使用的BIC准则以及所构造的目标函数R分别对原始数据以及AR（1）模型进行变点个数估计，如图2所示：

图2 变点个数估计

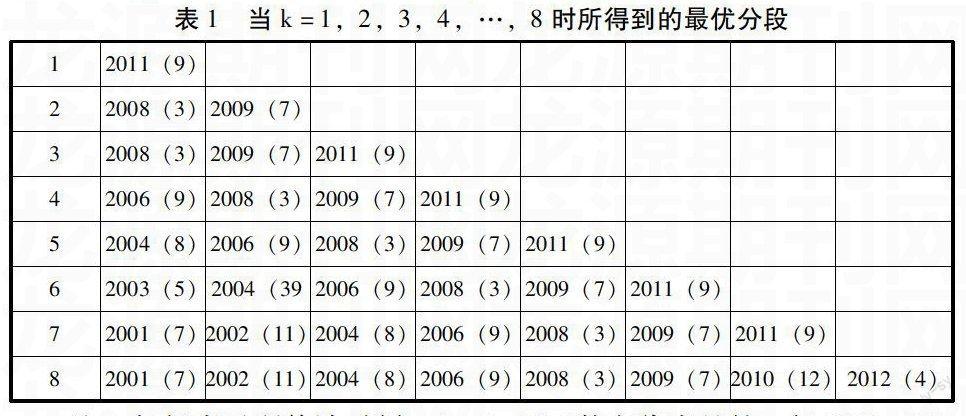
根据Bai和Perron（2003）[4][5]及陈希孺（1991）[6]的思想，由图2（左）可知对于BIC准则及目标函数R对原始数据所估计变点个数为7，而由图2（右），BIC准则对AR（1）模型估计变点个数为0，由目标函数R可知在k=7和k=8处变化不大，认为变点个数估计为7。因此，我们估计变点个数k=7。从而，通过前文的动态规划原理和最小二乘法对其变点位置以及各段系数进行估计，结果如表1所示。

表1 当k=1，2，3，4，…，8时所得到的最优分段

1 2011（9）

2 2008（3） 2009（7）

3 2008（3） 2009（7） 2011（9）

4 2006（9） 2008（3） 2009（7） 2011（9）

5 2004（8） 2006（9） 2008（3） 2009（7） 2011（9）

6 2003（5） 2004（39 2006（9） 2008（3） 2009（7） 2011（9）

7 2001（7） 2002（11） 2004（8） 2006（9） 2008（3） 2009（7） 2011（9）

8 2001（7） 2002（11） 2004（8） 2006（9） 2008（3） 2009（7） 2010（12） 2012（4）

注：加粗表示所估计时刻;（ ）里面数字代表月份，如2001（7）表示2001年7月。

（二）模型变点的原因分析

从图1我国月度CPI的走势图可以看出，十几年来我国月度CPI总体变化并不平稳，而是大起大落。由表1可知，对于CPI而言对应的变点分别为2001年7月、2002年11月、2004年8月、2006年9月、2008年3月、2009年7月和2011年9月附近。所得变点将时间段2000-2013年划分成8段，这些变点往往与当时的经济政策或经济动态相关联的，而分段往往对应其波动周期，接下来分析其经济意义及CPI的波动特征和周期。

2001年4月至2001年11月，CPI同比上涨1.5%，最高涨幅达到1.3%，总体平均涨幅水平为0.6526%，由于我国经济尚未从1998年亚洲金融危机恢复过来，从而CPI保持低水平涨幅运行，而在2001年8月至2002年11月，最高涨幅为1.0%，而最低涨幅达到-1.3%，总体平均涨幅为-0.5188%，CPI于负水平低位运行，说明在变点2001年7月前后，我国CPI由正水平进入负水平，结构发生了变化，一方面主要由于2001年我国加入WTO后，进口关税水平降低，对于我国物价水平下降的影响压力较大，我国农业受到严重冲击，出现严重的供大于求得矛盾，进一步加大物价的下降;另一方面国际石油价格的大幅度下降，也使我国CPI整体水平下降。

2002年10月至2003年3月，CPI同比上涨-0.7%，最高涨幅达到5.3%，总体平均涨幅水平达到2.1762%，这一时期我国CPI以正水平运行，为我国2000年以来第一次上涨阶段。因此，在2002年11月前后，我国CPI整体水平由负转正，一方面主要由于2002年下半年以来，我国的货币供应量和金融机构贷款的明显增加以及我国加大货币金融政策对经济发展的支持力度，有利于物价的回升;另一方面，2002年下半年，我国经济开始从1998年亚洲金融危机中解放出来及世界经济形势好转。

2003年10月至2005年1月，CPI同比上涨5.3%，最高涨幅达到5.2%，最低达到0.8%，总体平均水平达到1.9200%，在2004年8月前后，我国CPI整体水平虽然保持正水平，但相比而言出现下降趋势，一方面主要由于2004年下半年，我国粮食种植面积大幅度增加，使得粮食供求紧张局面得到缓解以及我国货币供给量降低;另一方面，国际原油价格趋降。

2006年7月至2007年3月，CPI同比上涨1.5%， 2006年10月至2008年3月，最高涨幅达到8.7%，为10多年来最高，总体平均水平达到4.8556%，为2000年以来我国CPI第二次上涨阶段，CPI持续高位运行，在2006年9月前后，CPI明显出现上涨趋势，一方面主要由于2006年下半年，我国房价快速上涨，虽然房价为未记入CPI，但是在这一轮经济增长中，房价的上涨带动了我国其他产业价格的快速上涨，并带动了整个市场商品价格的全面增长;另一方面，国际大宗商品供给趋紧以及原油价格开始攀升。

2007年10月至2008年6月，CPI同比上涨达到8.3%， 2008年4月到2009年7月，最高涨幅为8.5%，最低涨幅为-1.8%，整体平均水平达到2.4062%，虽然在2009年出现负增长，但是由于2008年的CPI高位运行，从而使得在此阶段整体平均仍然为正的，但显然在2008年3月前后，整体平均水平降低，一方面主要由于2008年发生国际金融危机以及国际原油价格大幅度降低，导致我国经济环境恶化，使得我国CPI持续降低;另一方面由于国际国内经济不景气，房市持续低迷，导致物价短时、深度下降。

2009年4月至2010年1月，CPI同比上涨-1.8%。2009年5月至2011年9月，最高涨幅达到6.5%，最低位-1.2%，整体平均水平为3.5038%，为我国2000年以来CPI第三次上涨阶段，相比2009年6月之前，整体水平提高，CPI开始回升，这是由于我国采取一系列的货币政策来拉动内需以减少金融危机对我国经济的影响，以及国际能源价格猛涨和全球范围内大宗农场品价格上扬。

2010年9月至2011年12月，CPI同比上涨6.1%，在2011年9月之后，最高涨幅达到5.5%，整体平均水平达到1.8889%，相比而言，全国CPI开始下降，主要由于2011年下半年，我国货币政策的收缩力度明显加大，货币因素开始对价格上涨起抑制作用;国际市场大宗商品价格在三季度的下跌和人民币持续升值。

四、总结

本文主要运用变点理论对全国（2000-2013）年月度CPI进行波动分析，通过变点分析可知我国CPI大致波动周期及特征，2000年以来，第一次下降持续了15个月左右;第二个下降期持续24个月左右;第三个下降期持续19个月左右;第一个上升期持续约23个月;第二个上升期持续约21个月;第三个上升期持续约26个月。从而可知，每次下降周期大概持续19个月左右，每次上升期周期大概持续23个月左右，说明我国CPI呈现出明显的周期性波动规律，且每次上升必然伴随着下次的下降，从2011年9月到2013年1月，下降持续约17个月，说明服从其波动周期。因此，研究我国居民消费价格指数的动态变化，掌握其变化规律，对于预测CPI走势及预防突发事件对CPI的影响具有重要意义。（作者单位：浙江财经大学数学与统计学院）

参考文献：

[1] 方燕，尹元生.我国居民消费价格指数波动特征的实证分析[J].价格理论与实践，2009，4： 56-57.

[2] 杨坚，费俊俊.我国居民消费价格指数走势实证分析与预测[J].统计与决策，2014，7： 112-116.

[3] 陈家清，张智敏，王仁祥.居民消费价格指数的非对称性波动及短期预测[J].统计与决策，2013，4： 119-122.

[4] Bai J，Perron P. Estimating and testing linear models with multiple structural changes[J].Econometrica，1998，66： 47-78.

[5] Bai J，Perron P. Computation and analysis of multiple structural change models[J].Appl.Econometrics，2003，18： 1-22.

[6] 陈希孺.变点统计简介[J].数理统计与管理，1991，2： 52-60.

[7] 王锦功，于维生.线性回归模型变点估计的动态规划方法[J].中国管理科学，1996，1： 59-63.

[8] Yao Y-C.Estimating the number of change-points via Schwarz' criterion[J].Statistics and Probability Letters，1988，3： 181-189.

[9] Guo H，Liu X，Song L.Dynamic programming approach for segmentation of multivariate time series[J].Stochastic Environmental Research and Risk Assessment，2014： 1-9.