动态规划最优控制在非线性系统中的应用

陈瑶张刚

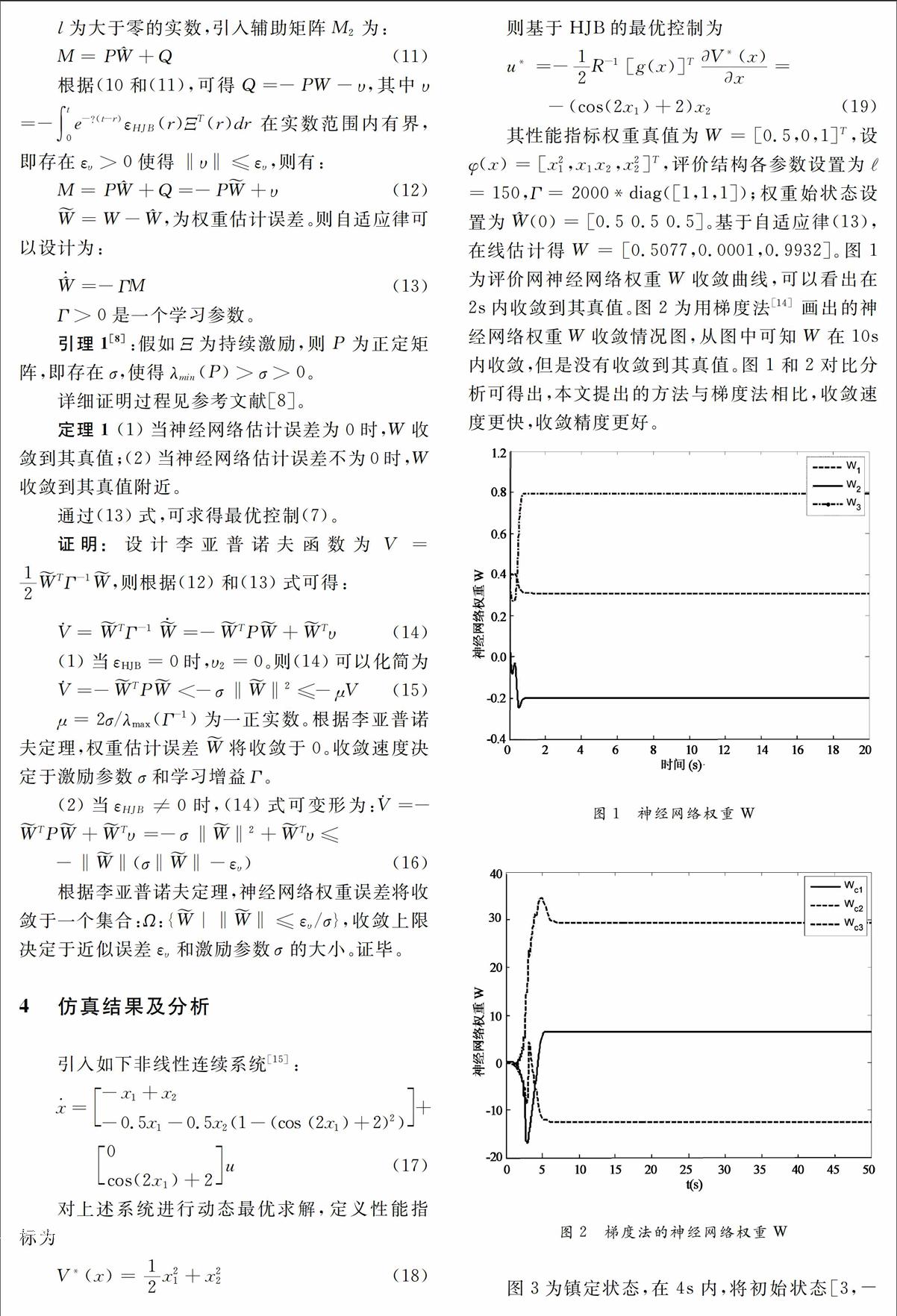
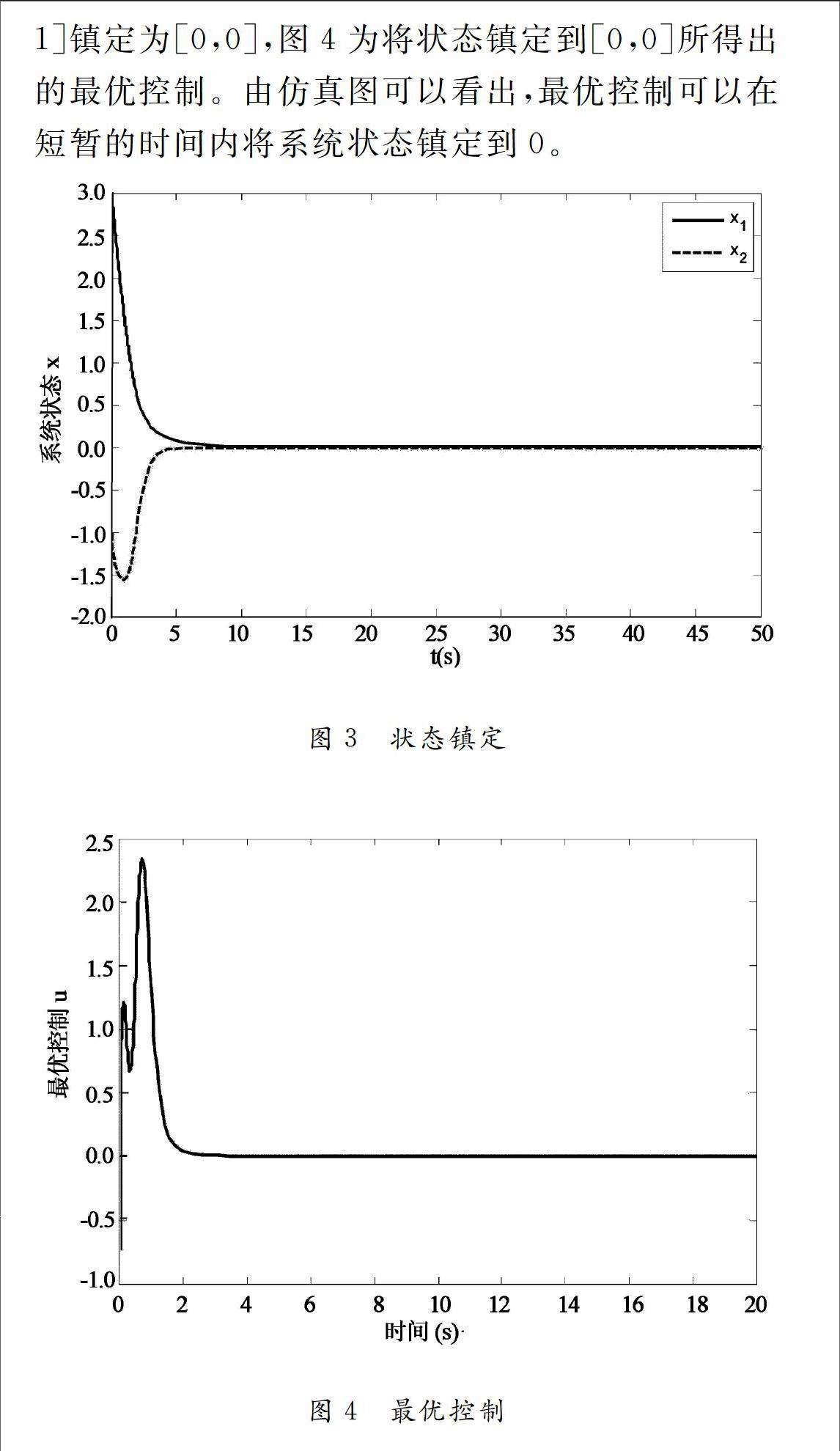
摘要：应用一种新的自适应动态最优化方法（ADP），在线实现对非线性连续系统的最优控制。首先应用汉密尔顿函数（HamiltonJacobiBellman， HJB）求解系统的最优控制，并应用神经网络BP算法对汉密尔顿函数中的性能指标进行估计，进而得到非线性连续系统的最优控制。同时引进一种新的自适应算法，基于参数误差，在线实现对系统进行动态最优求解，而且通过李亚普诺夫方法对参数收敛情况也进行详细的分析。最后，用仿真结果来验证所提出的方法的可行性。

关键词：最优控制；动态规划；神经网络；自适应算法；汉密尔顿函数

中图分类号：TP273.1文献标识码：A

1 引言

最优控制是最近几年国内外新起的一个研究领域，最优控制就是寻找最节能最经济的控制策略。50年代，美国数学家Bellman为了解决非线性最优控制问题提出了动态规划方法（Dynamic Programming）[1]。动态最优化方法就是将最优化问题分多级讨论，寻求每一级的最优策略，从而达到全局最优。然而在实际问题中对于大量存在的非线性系统，需要求解汉密尔顿函数（HJB），由于维数问题，求解函弥尔顿函数是个很难解决的问题。

强化学习（Reinforcement learning）[2]是基于生物学习的新型理论。通过比强化学习和动态规划，Werbos[3]提出了新的自适应动态规划方法，从而解决了离散系统的动态最优求解的“维数灾难”问题[1， 4]。然而传统的增强学习方法一般用来解决离散系统，实际问题往往是连续的。

文献[5]将增强学习方法和动态规划方法结合，提出了自适应动态规划方法（Adaptive dynamic Programming）。Werbos[6]基于增强学习方法，提出评价和执行网对离散系统进行动态最优求解。Lewis[7]提出了一种新的基于神经网络的自适应动态最优方法对离散非线性系统进行离线求解。

本文基于一种新的自适应动态规划算法在线解决了非线性系统的最优控制问题。首先应用HJB对非线性系统进行最优求解，进而基于神经网络方法对最优控制中的性能指标进行估计，即应用评价结构解决了动态最优控制问题，同时省去了传统最优控制求解问题中的执行机构，很大程度上缩短了计算机计算的时间。文中引用了一种新的自适应算法[8， 9]在线求得基于神经网络的评价网的权重参数。最后本文对估计权重做了基于李亚普诺夫的收敛性分析，很大程度上提高了论文所提出理论的使用价值。

5结论

引进一种新的自适应算法对非线性连续系统进行自适应动态最优求解。不同Werbos[6]提出的评价执行结构，本文基于辨识评价结构，在线对连非线性系统进行最优求解。用神经网络逼近性能指标，而且基于自适应估计误差，在线估计神经网络权重。比现有文献所用梯度法和迭代法收敛速度更快，而且收敛效果更加良好。仿真结果更加有力的证明所提出方法的有效性。

参考文献

[1]B. R. E， Dynamic programming， Princeton： Princeton University Press， 1957.

[2]SUTTON R S，BARTO A G.Reinforcement learning： an introduction. Cambridge Univ Press， 1998.

[3]WERBOS P J.Approximate dynamic programming for real-time control and neural modeling， Handbook of intelligent control： Neural[J].fuzzy， and adaptive approaches，1992， 15： 493-525.

[4]DREYFUS S E，LAW A M.Art and theory of dynamic programming[M].New York： Academic Press， 1977，56.

[5]MURRAY J J，COX C J，LENDARIS G G， et al. Adaptive dynamic programming， Systems， Man， and Cybernetics， Part C： Applications and Reviews[J]. IEEE Transactions on， 2002， 32（2）： 140-153.

[6]WERBOS P J.A menu of designs for reinforcement learning over time[J].Neural networks for control， 1990：67-95.

[7]ABUKHALAF M，LEWIS F L.Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach[J].Automatica， 2005， 41（5）： 779-791.

[8]NA J，HERRMANN G，REN X.， et al. Robust adaptive finitetime parameter estimation and control of nonlinear systems[J].IEEE International Symposium on in Intelligent Control （ISIC）， 2011： 1014-1019.

[9]Na. Jing， Ren. Xuemei， Zhang. Dongdong， Adaptive control for nonlinear purefeedback systems with highorder sliding mode observer[J]. IEEE transactions on neural networks and learning systems， 2013， 24（3）： 370-382.

[10]VAMVOUDAKIS K G，LEWIS F L.Online actorcritic algorithm to solve the continuoustime infinite horizon optimal control problem[J]. Automatica， 2010，46（5）：878-888.

[11]VRABIE D，LEWIS F.Neural network approach to continuoustime direct adaptive optimal control for partially unknown nonlinear systems[J]. Neural Networks， 2009，22（3）： 237-246.

[12]DIERKS T，THUMATI B T，JAGANNATHAN S.Optimal control of unknown affine nonlinear discretetime systems using offlinetrained neural networks with proof of convergence[J].Neural Networks， 2009，22（5）：851-860.

[13]LIU D，WEI Q.Finite approximation error based optimal control approach for discretetime nonlinear systems[J].IEEE Transactions on Cybernetics，2013，43（2）：779-789.

[14]BHASIN S，KAMALAPURKAR R，JOHNSON M， et al.A novel actorcriticidentifier architecture for approximate optimal control of uncertain nonlinear systems[J].Automatica，2013，49（1）：82-92， .

[15]NEVISTI V，PRIMBS J A.Constrained nonlinear optimal control： a converse HJB approach，1996.