浅谈数学教学中的数形结合

徐建飞

【摘要】"数形结合"思想方法是研究数学问题的重要方法，本文对初中数学中的部分问题，谈谈如何运用"数形结合"的思想解题。

【关键词】数形结合 数形结合思想 以形助数 以数解形

【中图分类号】G633. 6 【文献标识码】A 【文章编号】2095-3089（2015）14-0277-02

中学数学研究的对象可分为两大部分，一部分是数，一部分是形，但数与形是有联系的，这个联系称之为数形结合，或形数结合。我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事非。”“数”与“形”反映了事物两个方面的属性。我们认为，数形结合，主要指的是数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的。

作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，或者借助形的几何直观性来阐明数之间某种关系，即数形结合包括两个方面：第一种情形是“以数解形”，而第二种情形是“以形助数”。“以数解形”就是有些图形太过于简单，直接观察却看不出什么规律来，这时就需要给图形赋值，如邊长、角度等等，特别是在做选择题时，只有一个答案是正确答案，用此种方法就可能起到意想不到的效果。由于这“以数解形”比较简单，所以这里就不多做介绍了。“以形助数”是指把抽象的数学语言转化为直观的图形，可避免繁杂的计算，获得出奇制胜的解法。学生通常把“数形结合”就理解为“以形助数”，也可以这么说，理解了并掌握了“以形助数”这种思想方法，就是理解了“数形结合”。“以形助数”中的“形”，或有形或无形。若有形，则可为图表与模型，若无形，则可另行构造或联想。因此“以形辅数”的途径大体有三种：一是运用图形；二是构造图形；三是借助于代数式的几何意义。以下我将从 “数形结合”在哪些题型中可以应用和使用“数形结合”时要注意哪些事项这两个方面来具体介绍数形结合这种思想方法。

一、解决集合问题：在集合运算中常常借助于数轴、Venn图来处理集合的交、并、补等运算，从而使问题得以简化，使运算快捷明了。

例如：某班有54名同学，其中会打篮球的有36人，其余的不会；会打排球的人数比会打篮球的多4人，其余的不会；另外，这两种球都不会打的人数是都会打的人数的 还少1，问既会打篮球又会打排球的有多少人？

分析：用韦恩图画出示意图，借助图形去分析解决此问题，使复杂的问题简单化，借助方程去求解。

解析：不妨设54名同学组成的集合为S，会打篮球的同学组成的集合为A，会打排球的同学组成的集合为B，两种球都会打的同学组成的集合为C

设C中有元素x个即既会打篮球又会打排球的同学有x人

则 （36-x）+（40-x）+（ x-1）=54 则 x=9

所以说既会打篮球又会打排球的同学有9人.

通过图示先将无形的东西转化成有形，再将有形的东西转化成方程去求解是复杂的问题简单化

二、解决函数问题：借助于图象研究函数的性质是一种常用的方法。函数图象的几何特征与数量特征紧密结合，体现了数形结合的特征与方法。

例如，代数中，二次函数图象y=ax2+bx+c（a≠0）， △= .

当△>0 y=ax2+bx+c的图象与x轴有两个交点。

△=0 y=ax2+bx+c的图象与x轴有一个交点。

△<0 y=ax2+bx+c的图象与x轴无交点。

三、在理解数量关系及概念上的作用

初中数学有代数和几何两部分内容，它门是互相渗透与推进的，如代数列方程解应用题中的行程问题，往往借助几何图形，靠图形感知来“支持”抽象的思维过程，从而数量之间的相依关系，所以数形结合是寻找解决问题途径的—种思维方法。又如初一教材引入数轴，就为数形结合的思想奠定了基础。教材借助于数轴：（1）直观地给出了相反数的定义，在数轴上表示该两数的点分别在原点的两旁，离开原点的距离相等；零的相反数仍是零。（2）直观地给出了有理数大小的比较法则，即在数轴上表示的几个有理数，右边的数总比左边的数大，（3）直观地给出了“绝对值”的定义：一个数的绝对值是在数轴上表示—个数的点与原点的距离，因此，借助数轴使数和最简单的图形——直线上的点之间建立了对应关系，揭示了“数”与“形”之间的紧密内在联系，充分显示出数与形结合起来产生的威力，这种抽象与形象的结合，能使学生的思维得到锻炼。

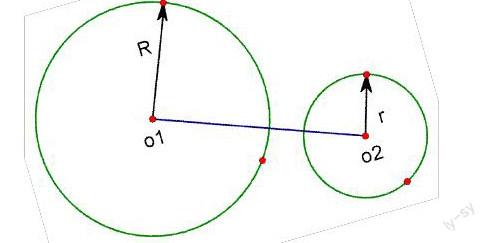
四、数形结合在平面几何中《圆》中的运用，点与圆的位置关系，直线与圆的位置关系，圆与圆的位置关系，也是通过数形联系来描述的。

例如：圆与圆的位置关系，设两圆的半径分别为R、r（R>r），圆心距为d，则

当d>R+r 两圆外离

当d=R+r 两圆外切

当R-r

当d=R-r 两圆内切

当d

这种描述，正是通过数形结合来揭示事物本质特征，既直观又能体现了运动变化的规律.“数”与“形”的教学不能孤立进行，而应是交错进行，相辅相成。

五、解决方程与不等式的问题：处理方程问题时，把方程的根的问题看作两个函数图象的交点问题；处理不等式时，从题目的条件与结论出发，联系相关函数，着重分析其几何意义，从图形上找出解题的思路。

在解题中应用数形结合能使解题速度快，思维敏捷。如求二次不等式 的解集，依代数方法是转化为解不等式 再转化为不等式组：

或 解之

但若以形代数，架起直觉思维之桥，其获得结论的速度是上述推导所望尘莫及的。其方法是：先求一元二次方程 的两根x1=-3，x2=1，

再画略图：

不等式 的解集，便一目了然。同时。又可以把三个“二次”即一元二次方程ax2+bx+c=0，二次函数y=ax2+bx+c（a≠0）及一元二次不等式通过图象直观地联系起来，而其系数a.b.c的几何意义，即a确定抛物开口方向，a與b确定对称轴位置（ ），c确定图象在y轴上的截距，都可以通过图象得到直观形象的解释。一旦学生能从数形的结合上把握三个“二次”的联系，那么就能加强对重要知识的理解与掌握，从而提高分析问题，解决问题的能力.

六、利用几何图形，帮助解决代数问题。

例1：在一块底长为a，高为h的三角形铁板ABC上，截出一块矩形铁板EFGH，使它的—边FG在BC上；求矩形铁板EFGH的面积S与矩形的边EF（设为x）之间的函数关系。

解：矩形EFGH EH‖BC △AEH∽△ABC

可得

由此

∴矩形铁板EFGH的面积S与矩形的边EF之间的函数关系为：

七、求最值

例2：如果实数 满足 则 的最大值为

分析：等式 有明显的几何意义，它表示坐标平面上的一个圆，

圆心为（2，0）半径 ，（如图），而 则表示圆上的点 与坐

标原点（0，0）的连线的斜率。如此一来，该问题可转化为如下几可问题：动点A

在以（2，0）为圆心，以 为半径的圆上移动。求直线OA的斜率的最大值，由图可见，当 在第一象限，且与圆相切时，OA的斜率最大，经简单计算，得最大值为

以上例1，例2说明了有关“数”方面的问题，借用“形”的性质之后，可以使许多抽象的关系直观化，形象化和简单化，也有助于对问题的内在联系更进一步的了解，从而变难为易，化繁为简. 同时，这对于帮助学生开阔思路，突破思维定势，有极好的作用。在学习过程中，有意培养学生的数形结合思维，往往更容易看清事物的本质，收到事半功倍的效果。

八、利用代数计算解决几何问题

例3： 已知⊙O内切于△ABC，AB=10，BC=13，AC=11.求：过△ABC的顶点A、B、C各点的切线长。

解：设⊙O与△ABC各边分别相切于点D、E、F，则

AD=AF，BD=BE，CE=CF

又设AD=x，BE=y，CF=z，则

x+y=10，y+z=13，z+x=11

解方程组： 得

∴过△ABC的顶点A、B、C各点的切线长分别为4，6，7。

例4：已知：三角形三边长a、b、c满足 ，

试确定三角形的形状。

解：∵

∴

∴

∴a=b，b=c，c=a 即a=b=c

∴该三角形是等边三角形。

由例3，例4说明几何方面的问题，如果借用代数方法解决，解题方法就易于寻找，解题过程也变得比较简便，因为几何题显然由形较直观，但若遇到已知和结论之间相距较远的问题，解题途径常常不易找到，因而用代数方法解题，思维就比较明确，有规律，因此也就容易找到解题方法。

总之，在数形转化过程中，必须遵循等价转换原则，数形互补原则。初中数学教材中，数形结合的例子很多，仅从举过的例子可以看出，代数，几何虽然各有不同特点和思考问题的方法，但是，完全有可能，有必要把它们的知识联系起来，因而我们数学教师应该在抓好代数，几何的基础知识的前提下，有意识地引导学生用数形结合的观点分析问题和解决向题，在此，应注意培养学生以下几点： （1）观察图形，挖掘图形中蕴含的数量关系。（2）正确绘制图形，反映图形中相应的数量关系。（3）切实把握“数”与“形”的对应关系，以图识性，以性识图。进而，加深对知识的理解与掌握，开拓思维。这种开拓思维对学生来讲，可称是创造，其思维的基础在于多次地完成数形沟通的训练，为创造思维积累了所需的潜在能量，在遇到新异问题时，才能闪现出创造性的火花。只要我们在教学中有意识地训练，不惜从点滴做起，坚持实践，学生思维素质便可望提高，同时，也为今后学习数学打下良好的基础.

数形结合的确是一个非常好，也非常实用而且重要的思想方法，应用性强。但它又是一把双刃剑，时时充满诱惑和危险。因此，我们要慎之又慎，要扬长避短，要全面合理分析，直观的同时，辅有严谨的演绎.

参考文献：

[1]林玉粦.用数形结合求函数的最值[J].福建中学数学，2001，4：24-25

[2]邱春来.数形结合法的应用及误差[J].福建中学数学，2004，2：29-31

[3]朱恩九.“以形辅数”的解题途径[J].数学通报，1994，4：33-35.

[4]苏元东.浅谈“以形助数”解题[J].福建中学数学，2005，2：27-28